超高层建筑涡激振动不稳定现象分析

王 磊， 蔺新艳， 梁枢果， 闫安志， 邹良浩

(1. 河南理工大学 土木工程学院，河南 焦作 454000； 2. 武汉大学 土木建筑工程学院，武汉 430072)

流体漩涡可能诱发结构的振动，早期水流涡振的研究结论认为[1-3]：当漩涡脱落频率与结构自振频率接近时，结构可能发生涡激共振现象；此时漩涡脱落频率会被结构频率控制而形成“锁定”现象；结构横向振动表现为大幅简谐振动，表面流体压力与结构位移的相位关系保持稳定。对高柔建筑的风致涡振来说，则有类似的研究结论。Kwok等[4]通过方形和圆形断面柱体的单自由度(Single Degree of Freedom, SDOF)气弹模型风洞试验发现，当涡激共振锁定现象发生时，结构的横风向振动为简谐振动，振幅大大增加。此后，有大量学者对超高层建筑横风向风致振动及气弹效应展开了研究。Steckley等[5-7]采用多种试验方式研究了方形、圆形、正三角形、正八角形截面高柔结构横风向气弹效应。Hayashida等[8]比较了高层建筑单自由度气弹模型和由高频测力方法得到的横风向位移响应的差别。Marukawa等[9]通过单自由度气弹模型风洞试验，分析了矩形截面高层建筑顺、横向气动阻尼随折算风速变化规律。我国Cheng 等[10-14]通过单自由度或多自由度(Multi Degree of Freedom, MDOF)气弹模型试验分析了高层建筑的横风向气动阻尼特性和涡振现象。

就超高层建筑横风向风效应研究的试验方式而言，既有有关涡激共振现象的研究多是以SDOF模型的方式进行的，这种试验方式观测到了较为理想的共振锁定现象。强迫振动试验是通过装置迫使测压刚性模型做简谐振动，本质上与SDOF模型的简谐共振情况是一致。既有高柔结构涡激共振响应评估模型的研究[15]，也是基于SDOF模型试验结果进行的，这些模型将涡激共振视为理想简谐振动。而MDOF气弹模型则主要用于气动阻尼、横风向风致响应(非共振)等方面的研究，尤其是作为试验方式应用到众多实际高层的抗风分析中[16-18]。总结而言，虽然MDOF气弹模型的试验方式已经得到了长足的发展，其试验精度的可靠性也已达成共识，但鲜有将MDOF气弹模型这一试验方式直接用于高层建筑或高耸结构的涡激共振研究。

事实上，SDOF模型作为研究高柔结构涡振现象的常用方式，其不精确性已被多次证实[19]，因而SDOF模型所观测到的理想“锁定”现象是值得推敲的。并且，部分SDOF模型的试验结果也表明，涡激共振只是接近而非理想简谐振动。圆截面高耸结构的实测资料也证实，涡激共振响应幅值存在较大波动。但是，超高层建筑或高耸结构涡激共振的不稳定性现象并未受到足够重视，尤其是不稳定现象的原因还未得到合理解释。鉴此，本文选择了多自由度气弹模型这一精度较高的试验方式，以更方便、真实地模拟高柔结构的不稳定共振现象，并对这种不稳定现象及其原因进行初步研究。

1 风洞试验概况

试验风场类型为均匀流和D类粗糙度流场，其中D类流场的风速和湍流度剖面，如图1所示。

图1 D类粗糙度流场风剖面Fig.1 Wind profile terrain category D

试验模型为方截面多自由度气弹模型，采用了立柱加刚性方板的设计思路，如图2所示。为满足铝板的刚度和质量要求，铝板选用厚10 mm的异形铝板；为保证模型的整体稳定性及弯曲振型所占成分，在模型中心设置了一方形强柱；四边有四根3～5 mm宽的细方柱，可以左右(前后)移动以调节刚度；为控制方柱的移动精度及牢固程度，在刚性方板侧面设置了若干卡槽；刚性铝板八个竖向螺孔可用于固定质量块；对较难实现的阻尼调节问题，采用在模型内部加泡沫条的方法进行。限于篇幅，有关该模型具体制作调试方法可参见文献[20]。试验模型共有三种高宽比，各模型的自振参数，如表1所示。由于模型的涡振是以一阶振型占绝对主导，表1中的频率均为模型一阶频率。测试内容为模型顶部风振位移和模型表面风压。

图2 气弹模型设计Fig.2 Design of MDOF model

表1为模型各工况自振参数，频率缩尺比约为100∶1，尺寸缩尺比为1∶600。表1中当量质量和Sc数的计算公式为

(1)

(2)

式中：m(z)为单位高度的模型质量；φ(z) 为平动振型;H为模型总高;ξs,ρa,D分别为结构阻尼比、空气密度和模型迎风面尺寸。

表1 模型参数

本文设计了一套吹气同步采样系统，来实现风压和位移的同步采集。在气流输入端吹气，经过“三通”

分流成两股气流，分别与扫描阀的一个通道和单点压力传感器连接，单点压力传感器与位移计连接在同一个数采板卡上。吹气时两个采样系统分别有一个通道的数据会在同一时刻出现脉冲峰，如图3所示。以此脉冲峰为起始点来截断数据，即实现了风压和位移的同步采集。

图3 同步脉冲信号Fig.3 Synchronization pulse

2 涡振不稳定现象

各工况模型顶部横风向位移响应随折算风速的变化情况，如图4所示。图4中，σy为模型顶部横风向均方根位移响应；Vr为折算风速，其计算公式为

(3)

式中：V为模型顶部风速；n1为模型在各试验风速下的一阶振动频率。

(a) 均匀流, 高宽比10

(b) D类流场, 高宽比10

(c) 均匀流, 高宽比13

(d) D类流场, 高宽比13

(e) 均匀流, 高宽比 16

(f) D类流场, 高宽比 16

既有研究表明，涡振响应水平与模型高宽比、模型密度及结构阻尼比有密切关系。从图4的试验结果可知：在均匀流和湍流场中，当折算风速达到共振临界风速时涡振位移响应最大；涡振位移随折算风速变化曲线呈倒“V”字状，且流场越光滑、Sc数越小，倒“V”字越尖锐。图5给出了部分风速下横风向位移响应时程。从图5可知：①在折算风速较小时，涡振位移时程具有很大的随机性，其幅值很不稳定；②随着折算风速的增大，涡振位移时程曲线规律性增强；当折算风速在临界风速附近时，位移时程的简谐性最好，但远非理想的简谐振动；③当折算风速继续增大，位移时程又重现出较明显的随机特性，但较之小风速(小于临界风速)下的时程，其振幅则相对稳定。

图5 共振前后位移响应时程(工况7，均匀流场)Fig.5 Time history of displacement response before and after the VIV

图6给出了部分工况在共振风速下的涡振位移时程。需要说明的是，由于本试验是以模型顶部风速为参考风速，因而不同风速剖面流场和不同高宽比模型涡振响应达到最大值时的折算风速有些一定差异。将图5和图6中不同高宽比、折算风速、流场粗糙度、斯科拉顿数(Sc)工况的涡振位移时程分别做对比可知，模型高宽比越大、Sc越小、流场越光滑、折算风速越接近共振风速则涡振幅值越稳定，简谐性越强。整体来看，各工况的涡振位移时程都与理想简谐振动有较大差距，涡振位移幅值随随时间变化有不同程度的波动，呈现为时而稳定、时而跳动的“葫芦波”，类似于“拍”的现象。可见，上述现象与既有试验现象和理论评估模型的理想共振情况是不同的，而与文献[21-22]及实测结果[23]是一致的。

图6 共振时位移响应时程Fig.6 Time history of VIV displacement

3 涡振不稳定原因分析

从“2节”分析可知，所谓不稳定性，其内涵有个两方面：①涡振位移响应在较长的持时下，只在某些时段内发生共振，而在其余时段则表现为很大随机性；②在共振段内，模型的振幅也不是一个稳定的值。本文称这一涡振现象为间歇性不稳定共振。这就是说，模型的振动情况一直是“瞬变”的。如前文所述，理想涡激共振最本质的特点是结构频率俘获了涡脱频率，使风压相位与位移相位关系保持恒定。下面将考察不稳定共振的瞬时频率和瞬时相位的特征，从而初步解释不稳定涡振现象的原因。

3.1 当理论涡脱频率等于体系振动频率时

首先以均匀流场中工况7在共振风速(Vr=10.44，V=10.5 m/s)下的情况为例，图7给出了同步归一化风压与位移的关系。图中风压数据是模型中上部两侧面全部测点风压的叠加，将其归一化之后，该风压时程与一阶广义力时程在规律上是一致的。位移和风压瞬时频率的计算方法为，将位移或风压时程按时间依次取为很多个0.4 s的时程段，对各段时程做傅里叶变换，可得到各段时程的瞬时频率。从而，将这些瞬时频率看成位移和风压响应在每一时刻的主频率。从图7可以看出，瞬时风压频率与位移频率并不是一个恒定的值，而是有很大幅度的波动，二者一致保持动态近似但不相等的关系。这说明，即便在同一来流风速下，位移和风压频率并不稳定，也没有构成一方“俘获”另一方的现象。

图8给出了风压与位移时程的局部放大图。从流固耦合的角度来说，模型大幅振动时气弹效应比较显著，并表现为风压很大程度受结构振动的影响，风压的变化反过来又会影响结构的振动，因而事实上二者是相互控制、互为激励的。从结构动力学角度来说，当共振现象发生时，荷载激励与系统振动频率的相位差近似为π/2。结合图8的结果，前文中模型振动位移和风压时程的不稳定性就得到了初步解释。具体来说，从某个时刻开始，位移与风压相位近似为π/2，此时的共振程度相对显著。此时，由于涡振位移的增大，负气动刚度会使体系振动频率将低[24-25]，使得位移相位逐渐滞后于风压相位。二者相位差别达到一定程度后，风压曲线突然变得较为随机，涡激共振不再继续，位移幅值和风压幅值开始逐渐减小。由于位移频率尤其是风压频率出现了一定的随机性，风压相位又会“遇到”了和其同步的位移相位，但此时的位移并没有突然增加，而是表现为逐渐增大，并伴随着风压相位与位移相位差的逐渐增加。就这样，二者幅值和相位周而复始地相互影响，最终造成了模型振动位移时程的间歇性和振动频率的不稳定性，并引起位移响应在“随机—过渡—共振”三者之间变换，这就解释了为什么实际振动不会出现理想的锁定现象。

(a)风压与位移瞬时频率

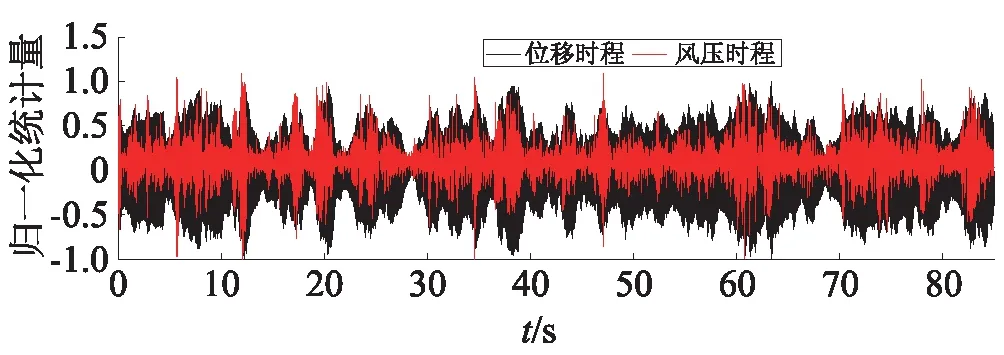
(b)同步风压与位移时程

(a)同步风压与位移时程

(b)风压与位移瞬时频率

图9～图11给出了D类湍流场中共振风速时的涡振风压和位移响应。可以看出，在D类湍流场中，涡振现象的不稳定性及其原因与均匀流场是一致的。所不同的是，由于湍流场风压时程和瞬时风压频率的波动更为明显，模型涡振(VIR(Vortex Induced Resonance)或VIV(Vortex Induced Vibration))位移响应也更不稳定，或者说保持稳定的持时较短。并且，湍流场中涡激共振发生时，横风向均方根位移响应比均匀流场要小。

从上述分析可知，瞬时风压频率与位移频率并不是一个恒定的值，即没有构成一方“俘获”另一方的“锁定”现象。说明实际共振并不是绝对理想的稳定共振，风压频率和位移频率的动态差异是涡激共振不稳定现象的直接原因。

图9 风压与位移瞬时频率(Vr=10.40，V=10.5 m/s， D类流场)Fig.9. Instantaneous frequency of pressure and displacement (Vr=10.40，V=10.5 m/s，terrain category D)

图10 同步风压与位移时程(Vr=10.40，V=10.5 m/s，D类流场)Fig.10 Synchronous time history of pressure and displacement (Vr=10.40，V=10.5 m/s，errain category D)

图11 风压与位移瞬时频率(Vr=10.40，V=10.5 m/s，D类流场)Fig.11. Instantaneous frequency of wind pressure and displacement (Vr=10.40，V=10.5 m/s，terrain category D)

3.2 当理论涡脱频率略小于体系振动频率时

以工况7为例，取Vr=9.84(V=10.0 m/s)的工况进行分析。从图12可知，当理论涡脱频率略小于体系振动频率时，风压频率整体上小于振动频率，但由于二者的动态变化，在很多时刻风压频率亦会等于或大于体系振动频率。

从图13可知：风压与位移相位关系与图8类似，也是从某个时候开始保持相等，而后风压相位逐渐滞后，如此往复变化造成了振动的间歇性。由于图13理论涡脱频率比振动频率要小，因而共振段的持时明显偏短，这就造成了此风速下涡振的间歇性相对显著。

图12 风压与位移瞬时频率(Vr=9.84，V=10.0 m/s，均匀流)Fig.12. Instantaneous frequency of pressure and displacement (Vr=9.84，V=10.0 m/s，uniform flow)

图13 同步风压与位移时程(Vr=9.84，V=10.0 m/s，均匀流)Fig.13 Synchronous time history of pressure and displacement (Vr=9.84,V=10.0 m/s, uniform flow)

3.3 当理论涡脱频率略大于体系振动频率时

取工况7、Vr=10.54(V=11.0 m/s)的工况进行分析。需要指出的是，V=11.0 m/s时的折算风速为Vr=10.54，这与V=10.5 m/s时的折算风速Vr=10.44差别不大，其的原因是结构主频率在不同来流风速下是有所变化的，这一点已在文献[24]中给出了讨论。

从图14可知，由于此时的名义涡脱频率大于体系振动频率，其风压频率整体上比振动频率要大，两频率维持近似相等的持时较短。从图15可知， 当风压与位移相位差别在左右时，涡振间歇性相对明显，且位移响应幅值逐步增大。由于风压频率整体大于体系振动频率，在较短的持时后，风压时程变得相对紊乱，位移响应也逐渐降低。如此往复，就形成了图15的曲线。

图14 风压与位移瞬时频率(Vr=10.54，V=11.0 m/s，均匀流)Fig.14 Instantaneous frequency of pressure and displacement (Vr=10.54，V=11.0 m/s， uniform flow)

图15 同步风压与位移时程(Vr=10.54，V=11.0 m/s，均匀流)Fig.15 Synchronous time history of pressure and displacement (Vr=10.54，V=11.0 m/s，uniform flow)

以上分析是以均匀流场为例进行的。在湍流场中，由于来流风速的脉动特性，理论涡脱频率会交替出现小于、等于和大于体系振动频率的三种情况。湍流场中的涡振现象可以看成是图7～图15分析的三种机制的共同作用。因而，湍流场中涡振的不稳定性就更为显著(见图6)。

4 结 论

本文通过分析风压与风振位移的瞬时频率及相位关系，初步揭示了高柔方柱涡振不稳定的直接原因。但上述频率及相位不稳定性的内在激发机制还有待进一步研究，比如，亦可以从非线性振动极限环理论的角度对此现象进行分析，这是下一步的工作。本文相关结论如下：

(1)当折算风速达到共振临界风速附近时，方截面超高层建筑的涡振现象可能发生。此时的横风向位移响应呈现出一定的简谐性，但远非理想的简谐振动。整体来看，涡振位移响应在较长的持时下，呈现为时而稳定、时而随机的“葫芦波”，是一种间歇性的共振。

(2)超高层建筑模型高宽比越大、Sc越小、流场越光滑、折算风速越接近共振风速则涡振幅值越稳定，简谐性越强。

(3)瞬时风压频率与位移频率并不是一个恒定的值，而是有很大幅度的波动，整体来看，二者一致保持动态近似但不相等的关系。说明即便在同一来流风速下，位移和风压频率并不稳定，也没有构成一方“俘获”或“锁定”另一方的现象。

(4)风压频率与体系振动频率的不稳定性是涡激振动不稳定的直接原因，且二者在某时刻相等之后难以保持相等，是的涡激振动在“共振”、“随机”及二者之间往复出现。

参 考 文 献

[ 1 ] KING R, PROSSER M J, JOHNS D J, et al. On vortex excitation of model piles in water[J]. Journal of Sound & Vibration, 1972, 29(2): 169-188.

[ 2 ] SARPKAYA T. Fluid forces on oscillating cylinders[J]. Nasa Sti/Recon Technical Report A, 1978, 78(3): 275-

290.

[ 3 ] BEARMAN P W. Vortex shedding from oscillating bluff Bodies[J]. Annual Review of Fluid Mechanics, 2003, 16(1): 195-222.

[ 4 ] KWOK K C S, MELBOURNE W H. Wind-induced lock-in excitation of tall structures[J]. Journal of the Structural Division, 1981, 107(1): 57-72.

[ 5 ] STECKLEY A, VICKERY B J, ISYUMOV N. On the measurement of motion induced forces on models in turbulent shear flow[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1990, 36(36): 339-350.

[ 6 ] VICKERY B J, STECKLEY A. Aerodynamic damping and vortex excitation on an oscillating prism in turbulent shear flow[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1993, 49(1): 121-140.

[ 7 ] VICKERY B J, STEKLEY A. Motion-induced forces on prismatic structures in turbulent shear flow[C]∥Proceedings of the Second International Conferences on Engineering Aero-Hydroelasticity. Pilsen: University of Western Bohemia, 1994.

[ 8 ] HAYASHIDA H, MATAKI Y, IWASA Y. Aerodynamic damping effects of tall building for a vortex induced vibration[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1992, 43(1/2/3): 1973-1983.

[ 9 ] MARUKAWA H, KATO N, FUJII K, et al. Experimental evaluation of aerodynamic damping of tall buildings[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1996, 59(2/3): 177-190.

[10] CHENG C M, LU P C, TSAI M S. Acrosswind aerodynamic damping of isolated square-shaped buildings[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2002, 90(12/13/14/15): 1743-1756.

[11] 梁枢果, 顾明, 张锋, 等. 三角形截面高柔结构横风向振动的风洞试验研究[J]. 空气动力学学报, 2000, 18(2): 172-179.

LIANG Shuguo, GU Ming, ZHANG Feng, et al. A study on across-wind oscillations of triangular high-rise flexible structures by wind tunnel tests[J]. ACTA Aerodynamica Sinica, 2000, 18(2): 172-179.

[12] 梁枢果, 吴海洋, 陈政清. 矩形超高层建筑涡激共振模型与响应研究[J]. 振动工程学报, 2011, 24(3): 240-245.

LIANG Shuguo, WU Haiyang, CHEN Zhengqing. Investigation on model and responses of vortex-induced resonances of rectangular super high-rise buildings[J]. Journal of Vibration Engineering, 2011,24(3):240-245.

[13] HUANG P, QUAN Y, GU M. Experimental study of aerodynamic damping of typical tall buildings[J]. Mathematical Problems in Engineering, 2013, 2013: 1-9.

[14] 全涌, 顾明, 黄鹏. 超高层建筑通用气动弹性模型设计[J]. 同济大学学报(自然科学版), 2000, 29(6): 112-

116.

QUAN Yong , GU Ming , HUANG Peng. Design of super-high rise buildings’global aeroelastic model[J]. Journal of Tongji University(Natural Science)， 2001, 29(1): 122-

126.

[15] SIMIU E, SCANLAN R H. Wind effects on structures: an introduction to wind engineering[M]. New York:Wiley, 1996.

[16] 王磊, 梁枢果, 邹良浩, 等. 某拟建838 m高楼多自由度气弹模型风洞试验研究[J].湖南大学学报(自然科学版), 2015, 42(1): 9-16.

WANG Lei, LIANG Shuguo, ZOU Lianghao, et al. Investigation of the wind-induced Responses of a tower 838 m high based on a multi-degree-of freedom aero-elastic model wind tunnel test[J]. Journal of Hunan University(Natural Sciences), 2015, 42(1): 9-16.

[17] 顾明, 周印, 张锋, 等. 用高频动态天平方法研究金茂大厦的动力风荷载和风振响应[J]. 建筑结构学报， 2000, 21(4): 55-61.

GU Ming，ZHOU Yin，ZHANG Feng, et al. Study on wind loads and wind-induced vibration of the Jinmao Building using high frequency force balance method[J]. Journal of Building Structures, 2000, 21(4): 55-61.

[18] KIM Y M, YOU K P, KO N H. Across-wind responses of an aeroelastic tapered tall building[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2008, 96(8):1307-1319.

[19] AAF A, MN B, KRC A, et al. Wind tunnel study of an oscillating tall building[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1995, 57(2/3): 249-260.

[20]王磊, 梁枢果, 邹良浩, 等. 超高层建筑多自由度气弹模型的优势及制作方法[J]. 振动与冲击，2014, 33(17): 25-31.

WANG Lei，LIANG Shuguo，ZOU Lianghao，et al. The advantages and making method of super high-rise building’s multi-DOF aero-elastic model[J]. Journal of Vibration and Shock, 2014, 33(17): 25-31.

[21] TAMURA T, DIAS P P N L. Unstable aerodynamic phenomena around the resonant velocity of a rectangular cylinder with small side ratio[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2003, 91(1/2):127-138.

[22]吴海洋. 矩形截面超高层建筑涡激振动风洞试验研究[D]. 武汉： 武汉大学，2008.

[23]RUSCHEWEYH H , GALEMANN T. Full-scale measurements of wind-induced oscillations of chimneys[J]. Journal of Wind Engineering Aerodynamics, 1996, 65(1): 55-62.

[24] WANG L, LIANG S, SONG J, et al. Analysis of vortex induced vibration frequency of super tall building based on wind tunnel tests of MDOF aero-elastic model[J]. Wind & Structures an International Journal, 2015, 21(5): 523-536.

[25]王磊, 梁枢果, 邹良浩, 等. 超高层建筑涡振过程中体系振动频率[J]. 浙江大学学报(工学版)， 2014, 48(5): 805-812.

WANG Lei， LIANG Shuguo， ZOU Lianghao， et al. Investigation on VIV system vibration frequency of super high-rise building [J]. Journal of Zhejiang University (Engineering Science), 2014, 48(5): 805-812.