MnO电子结构和磁性的第一性原理研究

陆彦功，赵 辉

（天津师范大学 物理与材料科学学院，天津 300387）

过渡金属氧化物作为一种莫脱（Mott）绝缘体，近年来一直受到广泛的关注[1-2].研究人员发现，与其他无磁性的普通氧化物相比，其具有许多特殊性质，如铁磁性或反铁磁性、超交换相互作用、高压下伴随高低自旋跃变发生的绝缘体-金属相变等[3-6].但过渡金属原子中d电子层电子排布紧密，具有强关联相互作用，不满足能带理论中单电子近似的假设，导致利用局域密度近似（LDA）和广义梯度近似（GGA）方法处理交换关联作用项时，对此类物质的性质出现了错误估计，得出它们是金属的错误结论.为了修正这些计算结果，考虑到实际存在的d轨道电子间的强相互作用，引入赫伯德（Hubberd）近似参数U[7]，即通过LDA+U方法得到较为可信的计算结果[8].这种方法降低了计算误差，同时保留了以LDA方法处理交换关联项时易于计算的特性，至今仍被大量用于计算模拟中.此外，与GGA+U方法相比，LDA+U得出的结果误差明显较小，与实验结果相近[8-9]，因此，本研究选择LDA+U方法计算MnO的相关性质.

此外，使用基于LDA+U方法的局域自旋密度近似（LSDA）+U方法可以更好地模拟MnO的物理特性[10-11].与更复杂的杂化泛函（HSE）方法所得能带[12]相比，LSDA+U方法虽然低估了能带带隙值，但计算量大大减少，且能带分布与其一致，所以本研究使用LSDA+U方法计算MnO的能带分布.文献[11]使用全电子势LSDA+U方法得到了与实验相符的晶格常数，本研究利用赝势法算出的晶格常数相对偏小，但鉴于赝势法计算量小，又可与已有全电子法计算所得电子结构方面的结果相匹配，所以利用赝势法处理核外电子，再结合LSDA+U方法处理交换关联能，可以做到对MnO的性质进行简易分析.

1 计算方法与模型

1.1 第一性原理计算方法与模型

本研究使用基于密度泛函理论的vasp程序包，结合程序提供的投影缀加波（PAW）赝势[13-14]，通过LDA处理交换关联能模拟面心立方MnO的不同磁结构.为保证计算的可信度，分别测试各种结构下的截断能和k点网格.为了方便比较，截断能统一选为500 eV.面心立方MnO的5种磁结构如图1所示，其中，FM对应铁磁结构，AFM1对应100面反铁磁，AFM2对应111面反铁磁，AFM3对应双层111面反铁磁，AFM4对应双层100面反铁磁结构.对应图1中5种磁结构，采用Monkhorst-pack取样法[15]分别选取k点网格为9×9×9（FM，AFM2），8×8×6（AFM1），8×8×3（AFM3）和 6×8×4（AFM4），最终使总能量均收敛到 1 meV/atom以下.

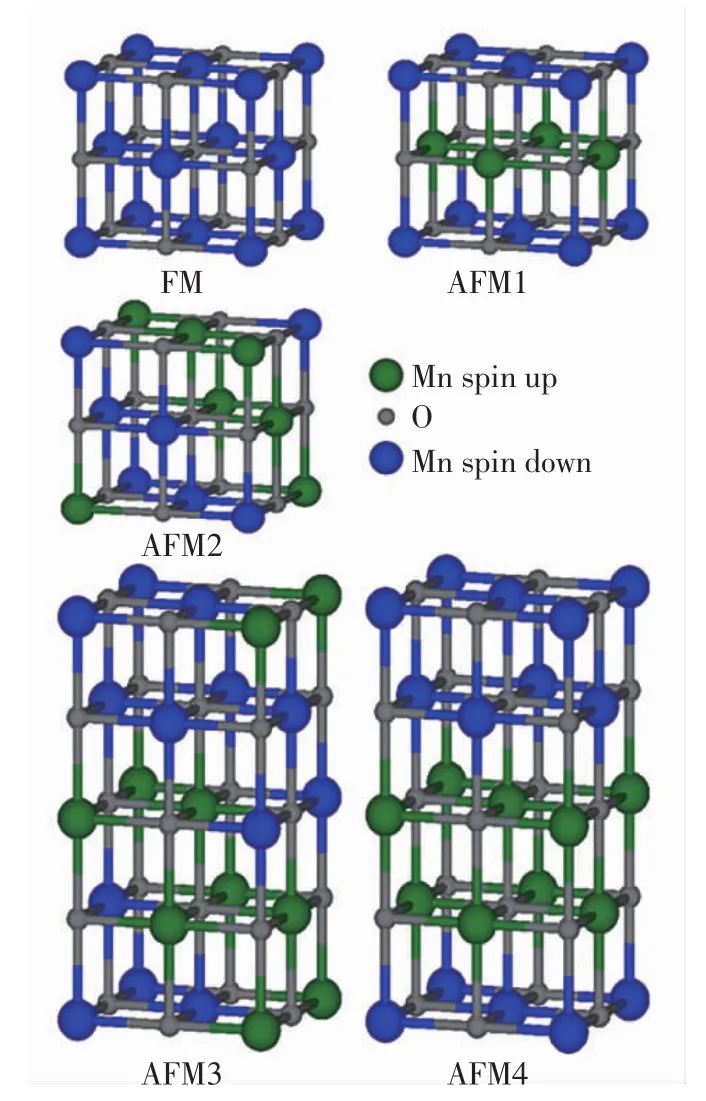
图1 面心立方MnO的5种磁结构Fig.1 Five different magnetic structures of MnO in face-centered cubic

应用由Liechtenstein等[10]提出的LSDA+U方法描述Mn原子中3 d电子的性质，选取库仑相互作用参数U=6.9 eV，原子内d-d轨道相互作用参数（洪特规则）J=0.86 eV[16].对应各个原子选取的PAW赝势分别为 Mn（3p63d54s2）和 O（2s22p4），即对 Mn 取 13 个外层电子作为价电子，O取6个作为价电子.

1.2 磁性质计算方法与模型

为了研究体系的磁性质，使用海森堡模型模拟磁性原子间的磁相互作用，利用第一性原理计算出的磁交换系数，结合蒙特卡罗（Monte-Carlo）方法计算温度变化时体系磁性质的变化情况，模拟该物质在温度变化时比热容的变化，给出相应的奈尔（Neel）温度，具体过程如下.

海森堡自旋哈密顿量可以表示为

式（1）中：交换作用系数J＞0时，交换作用倾向于铁磁性；J＜0时，交换作用倾向于反铁磁性.分别考虑不同磁结构中体系的哈密顿量，如果体系的结构无显著变化，则各个哈密顿量间的能量差就可以认为是由海森堡自旋哈密顿量彼此不同引起的.

利用Metropolis蒙特卡罗方法可以模拟海森堡模型给出磁性原子间的磁交换相互作用[17].具体过程为：建立1个三维空间点阵，每个空间格点代表1个磁性离子；为每个格点上的离子给定1个初始磁矩，然后随机反转某格点处的磁矩，利用Metropolis方法给出的判据确定该处离子的磁矩；经过大量随机反转操作即可通过海森堡模型得出该温度下体系的磁结构以及不同温度下体系的磁结构变化，模拟出体系的奈尔温度等磁性质.

2 结果及分析

2.1 状态函数拟合

对应图1中5种磁结构，通过改变原胞体积，分别计算体积变化后引起的原胞能量变化，再通过拟合Birch-Murnaghan状态函数[18]，得到原胞能量-体积分布曲线，结果如图2所示.由图2可知，不同磁结构对应不同原胞能量，但由此引起的能量差异较小.比较图2（a）和图2（b）可知，MnO晶格结构的形变不明显，对体系能量的影响很微弱，这与文献[19]中的描述相符，故可以忽略不计.因此，表1给出理想晶格结构下拟合所得体系平衡状态性质.由表1中数据可知，不同磁结构对晶格结构中原子的排布方式影响不大，不会显著影响原子在晶胞中的相对位置[20].在这种情况下，得出能量最低的结构对应的晶格常数为0.438 9 nm.由于磁结构的不同没有引起晶格结构发生显著变化，因此可以固定晶格常数并取各种磁结构对应的理想结构，然后比较各个结构间的能量差异，利用海森堡模型得出磁交换系数J.这种方法可以忽略晶格扭曲对原胞能量的影响，从而大大降低了问题的复杂性.

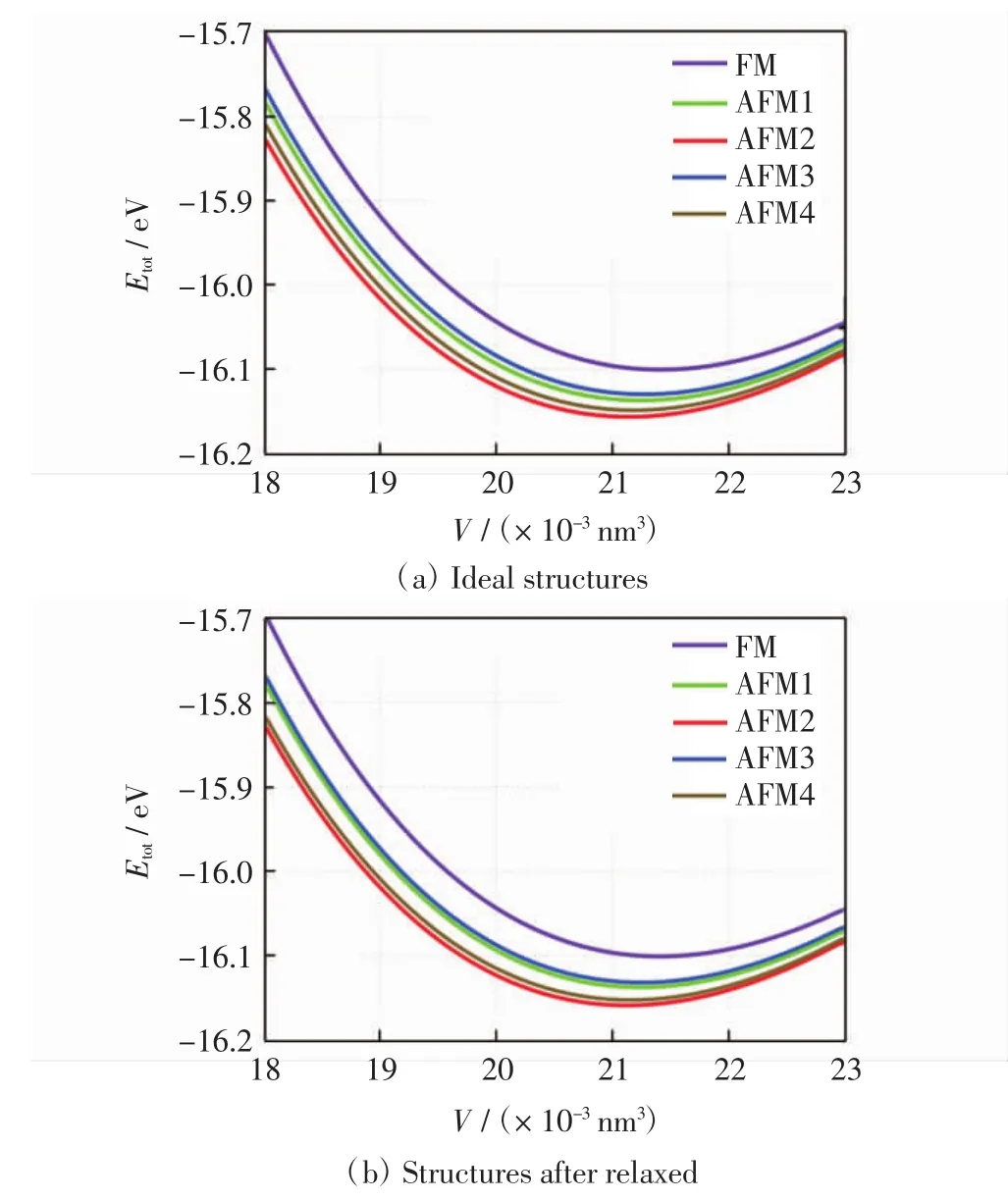
图2 MnO原胞能量Etot与原胞体积V变化的关系Fig.2 Total energy Etotvs.volume V per primitive cell for MnO in different magnetic orderings

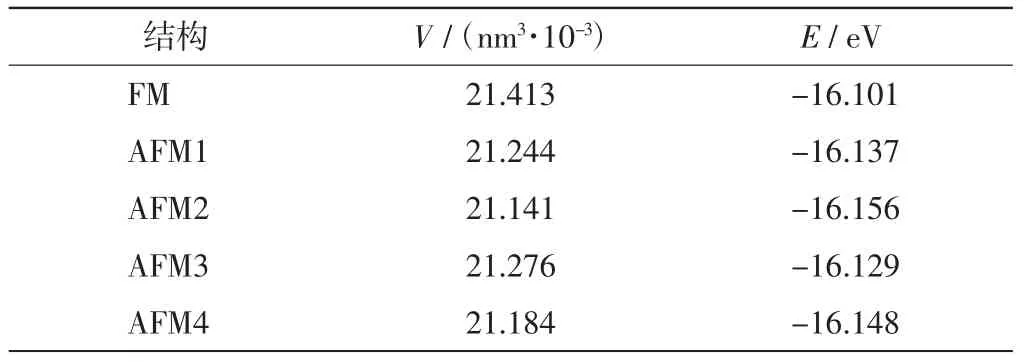
表1 状态函数拟合结果Tab.1 Fitting results of state equation

2.2 能带结构

为了探究MnO体系在不同自旋排布情况下电子结构的变化，分别计算了5种磁结构体系的能带结构.高对称点路径选取依照面心立方结构对应的倒空间结构，并按照文献[21]取完整路径.图3和图4分别为MnO在铁磁（FM）结构和4种反铁磁（AFM）结构下的能带结构，其中Eg表示带隙值，Ef表示费米能级对应的能量，E表示能量.由于铁磁情况下，自旋向上和向下的能带图具有显著不同，故在图3中分别予以绘制.反铁磁构型中自旋向上与向下情况的能带结构完全相同，故图4只给出自旋向上（或向下）电子的能带结构.

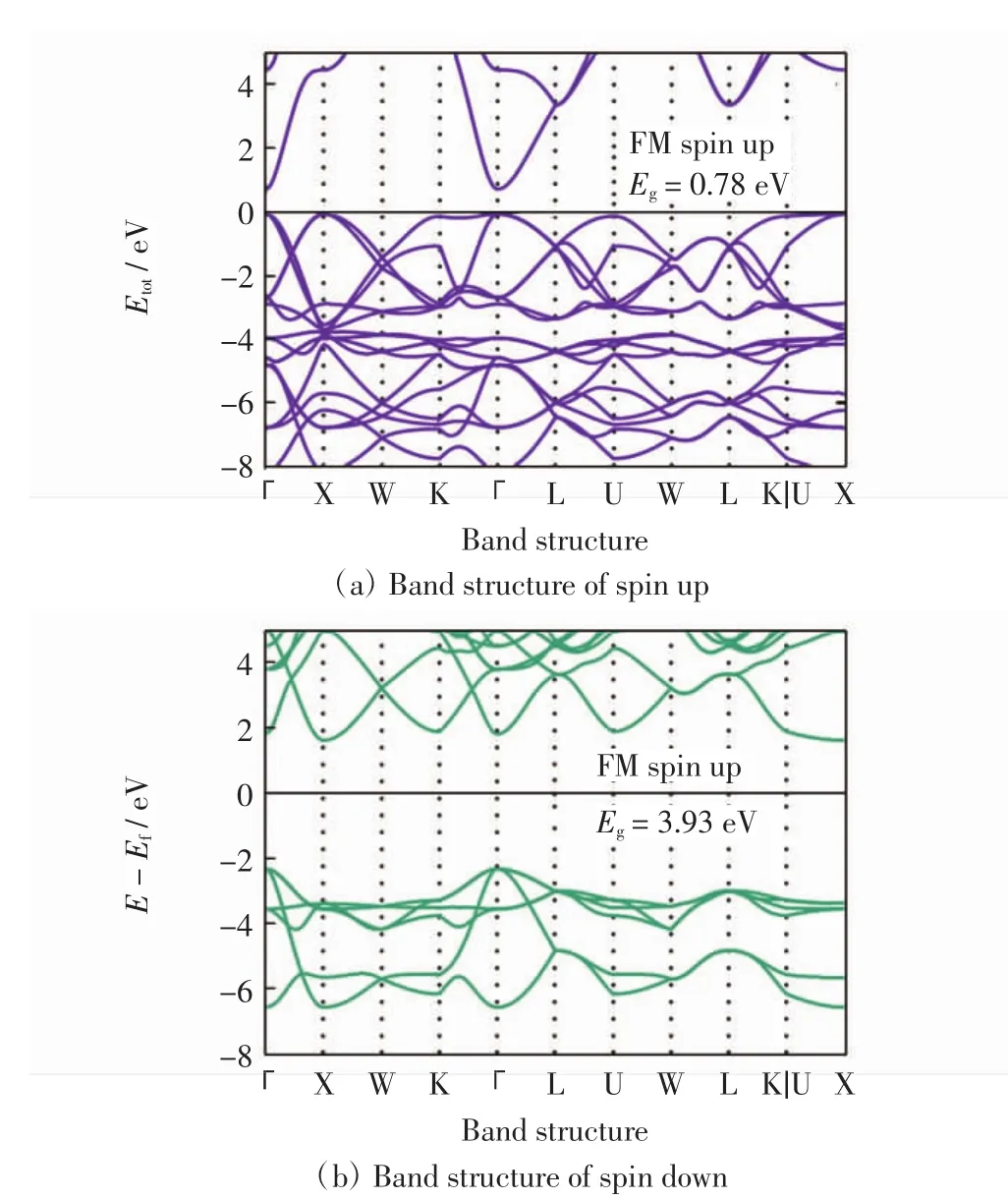
图3 MnO在铁磁结构下的能带图Fig.3 Band structure of MnO in FM

对比图3（a）和图3（b）可知，铁磁情况下，自旋排布使体系的轨道发生分裂，符合斯通纳（Stoner）模型中自发磁化产生强铁磁性的情况，满足发生自发磁化的斯通纳条件[7].比较图3和图4可知，铁磁结构与各种反铁磁结构相比，能带明显较宽，说明其中电子有效质量更小，电子运动更活跃，即铁磁结构比反铁磁结构更不稳定，这与图2所得结论相符.

比较图4（a）～图4（d）中 4 种反铁磁结构可知，磁结构对体系的电子排布有显著影响.体系的能带结构、带隙大小、带宽以及价带顶的位置均随其发生明显变化.仔细探究可知，能带带宽越窄，电子有效质量越大，带隙越宽，体系结构越稳定.结合表1中数据可知，结合能越小意味着越大的平衡态体积，在固定体积和磁结构的情况下，电子重新调整分布方式以达到最稳定状态，从而引起能带结构的重新排布.此外，使用赝势法结合LSDA+U计算所得带隙值与实验值相比仍然显著偏小，这是该方法自身缺陷引起的[22].

2.3 磁性质

根据前述海森堡模型，在不考虑晶格扭曲的情况下，比较不同磁排列情况下的能量差，考虑最近邻、次近邻、三阶及四阶近邻相互作用，不考虑磁相互作用时体系的哈密顿量为H0，则

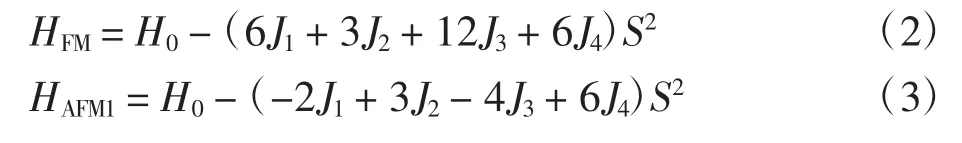
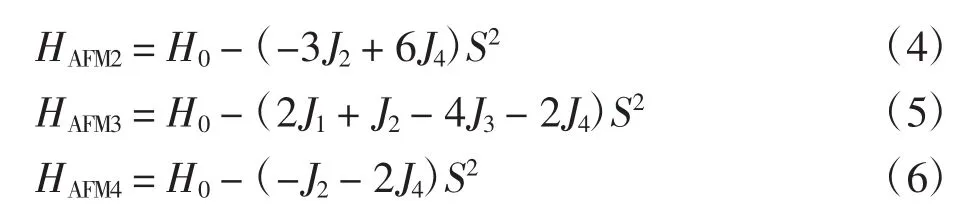
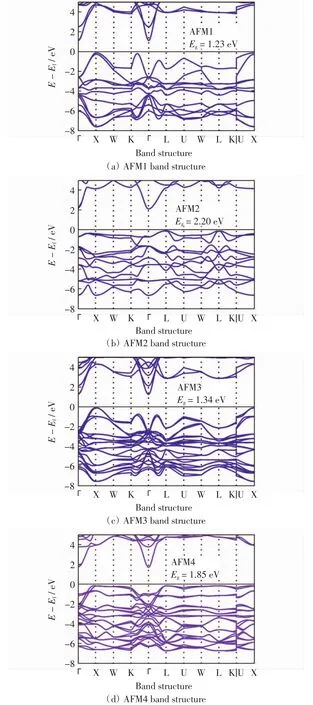
图4 MnO在4种反铁磁结构下的能带图Fig.4 Band structures of MnO in AFM1-4

实验表明，铁族盐中原子存在所谓的“轨道淬灭”现象[7]，因此，对于 MnO 晶体，式（2）～式（6）中，S可取5/2.由此对5个体系的能量进行比较，可得J1、J2、J3和 J4的值，分别为-8.786、-9.858、0.030 和-0.164，单位为开尔文（K）.通过计算磁体的交换系数[23-24]，进而得出对应磁体的奈尔温度.可供使用的方法包括平均场近似、随机相近似和经典蒙特卡罗模拟等[23].本研究选择经典蒙特卡罗方法进行模拟，利用正则系综[25]进行分析，可得

式（7）和式（8）中：N为磁性离子数；kB为玻尔兹曼常数；T为温度；E为能量；m为离子磁矩；Cν为磁比热；χ为磁化率.由此，建立16×16×16空间格子，结合晶格周期性，分析温度逐渐上升和逐渐下降2种情况，通过模拟得到磁比热Cν及磁化率χ随温度的变化情况分别如图5和图6所示.

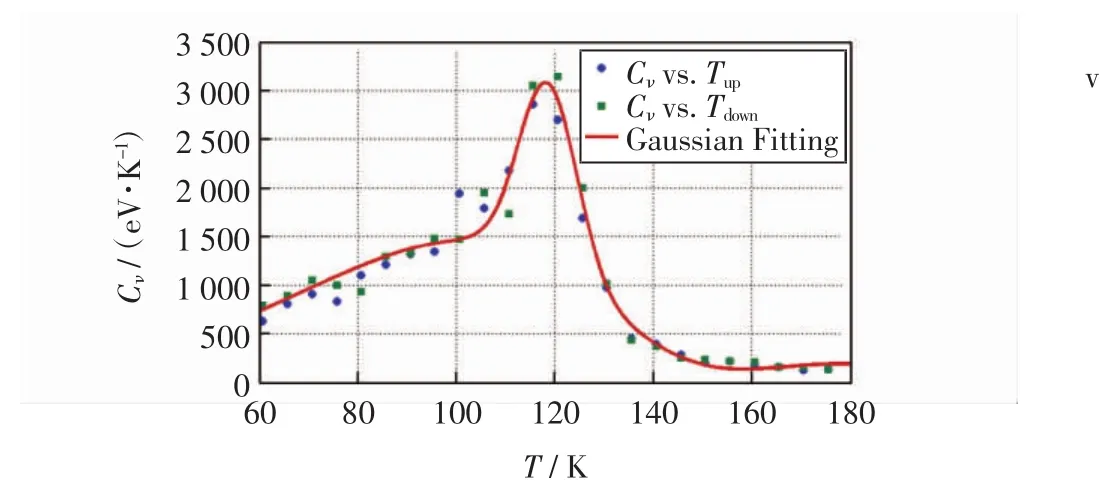
图5 磁比热与温度变化的关系图Fig.5 Results for magnetic specific heat vs.the room temperature about MnO

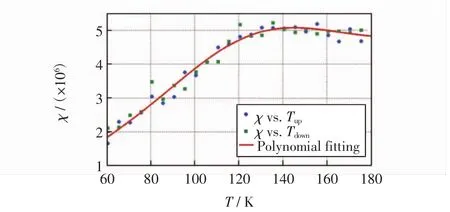
图6 磁化率与温度变化的关系图Fig.6 Results of magnetic susceptibility vs.room temperature

由图5可以看出，磁比热大约在环境温度达到115 K时达到最大，这与MnO奈尔温度的实验值117.9 K[26]非常接近，说明本研究模拟MnO磁性所采用的方法精确度较高，可用于模拟理想结构下过渡金属氧化物的磁性质.由图6可以看出，计算结果与实验结果[26]符合良好.比较已有GGA+U研究数据[19，26-27]，使用本研究所述方法可以相对精确地模拟MnO的磁性质，结果如表2所示.

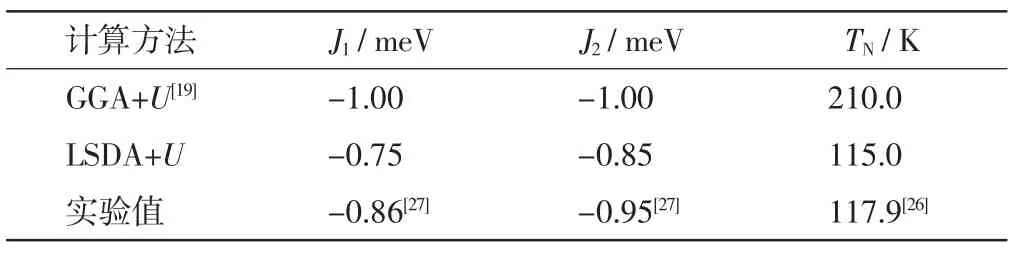
表2 面心立方MnO最近邻次和近邻交换常数J1、J2以及对应的奈尔温度TNTab.2 Nearest and next-nearest-neighbor exchange coupling constants J1and J2for MnO in face-centered cubic lattice as well as the resulting Néel temperatures TN

3 结论

利用第一性原理LSDA+U方法计算了典型莫脱绝缘体MnO因磁结构不同引起的能带结构变化，结合海森堡模型，利用蒙特卡罗方法分析了MnO的磁性质.计算结果表明：MnO的磁排布不同会导致体系结构发生变化，但变化一般较微弱.磁排布方式的不同显著影响了体系的电子排布，能带结构因此发生明显变化.考虑能量和结构相近的磁排布方式，在理想情况下进行比较可以得到较为准确的海森堡磁交换系数，进而模拟得到MnO奈尔温度和磁比热数值，所得结果与实验数据非常接近.根据文献[8]的结论，并比较已有GGA+U数据[19]，可知LSDA+U处理具有强相互作用的过渡金属氧化物精度更高，且适用于计算体系的磁性质.

[1]COHEN R E，MAZIN I I，ISAAK D G.Magnetic collapse in transition metal oxides at high pressure：Implications for the earth[J].Science，1997，275：654-657.

[2]KUNES J，LUKOYANOV A V，ANISIMOV V I，et al.Collapse of magnetic moment drives the Mott transition in MnO[J].Nature Materials，2008，7：198-202.

[3]KOLORENCJ，MITASL.Structural（B1 to B8）phase transition in MnO under pressure：Comparison of all-electron and pseudopotential approaches[J].Physical Review B，2007，75（235118）：1-7.

[4]BYCZUK K，HOFSTETTER W，VOLLHARDT D.Competition between Andersonlocalizationandantiferromagnetismincorrelatedlatticefermion systemswithdisorder[J].PhysicalReview Letters，2009，102（146403）：1-4.

[5]LEONOV I，POUROVSKII L，GEORGES A，et al.Magnetic collapse and the behavior of transition metal oxides at high pressure[J].Physical Review B，2016，94：1-6.

[6]TOMCZAKJM，MIYAKET，ARYASETIAWANF.Realisticmany-body models for manganese monoxide under pressure[J].Physical Review B，2010，81（11）：760-762.

[7]黄昆.固体物理学[M].北京：高等教育出版社，1988.HUANG K.Solid State Physics[M].Beijing：Higher Education Press，1988（in Chinese）.

[8]LOSCHEN C，CARRASCO J，NEYMAN K M，et al.First-principles LDA+U，and GGA+U，study of cerium oxides：Dependence on the effective U parameter[J].Physical Review B，2007，75（3）：5115.

[9]TERAKURA K，OGUCHI T，WILLIAMS A R，et al.Band theory of insulating transition-metal monoxides：Band-structure calculations[J].Physical Review B，1984，30（8）：4734-4747.

[10]LIECHTENSTEIN A I，ANISIMOV V I，ZAANEN J.Density-functional theory and strong interactions：Orbital ordering in Mott-Hubbard insulators[J].Physical Review B，1995，52（8）：R5467-R5470.

[11]DUDAREVSL，BOTTONGA，SAVRASOVSY，etal.Electron-energyloss spectra and the structural stability of nickel oxide：An LSDA+U study[J].Physical Review B，1998，57（3）：1505-1509.

[12]HAY P J，MARTIN R L，UDDIN J，et al.Theoretical study of CeO2and Ce2O3using a screened hybrid density functional[J].Journal of Chemical Physics，2006，125（3）：332-1046.

[13]BLÖCHL P E.Projector augmented-wave method[J].Physical Review B，1994，50（24）：17953-17979.

[14]KRESSE G，JOUBERT D.From ultrasoft pseudopotentials to the projector augmented-wave method[J].Physical Review B，1999，59（3）：1758-1775.

[15]MONKHORST H J.Special points for Brillouin-zone integrations[J].Physical Review B，1976，16（4）：1748-1749.

[16]ANISIMOV V I，ZAANEN J，ANDERSEN O K.Band theory and Mott insulators：Hubbard U instead of Stoner I[J].Physical Review B，1991，44（3）：943-954.

[17]METROPOLIS N，ROSENBLUTH A W，ROSENBLUTH M N，et al.Equation of state calculations by fast computing machines[J].Journal of Chemical Physics，1953，21（6）：1087-1092.

[18]BIRCH F.Finite elastic strain of cubic crystals[J].Physical Review，1947，71（11）：809-824.

[19]SCHRÖN A，RÖDL C，BECHSTEDT F.Energetic stability and magnetic properties of MnO in the rocksalt，wurtzite，and zinc-blende structures：Influence of exchange and correlation[J].Physical Review B，2010，82（16）：4325-4329.

[20]SCHRÖN A，RÖDL C，BECHSTEDT F.Crystalline and magnetic anisotropy of the 3d-transition metal monoxides MnO，FeO，CoO，and NiO[J].Physical Review B，2012，86（11）：5136-5141.

[21]SETYAWAN W，CURTAROLO S.High-throughput electronic band structure calculations：Challenges and tools[J].Computational Materials Science，2010，49（2）：299-312.

[22]ELP J V，ESKES H，POTZE R H，et al.The electronic structure of MnO[J].Physical Review B，1991，44（44）：1530-1537.

[23]FISCHER G，DÄNE M，ERNST A，et al.Exchange coupling in transition metal monoxides：Electronic structure calculations[J].Physical Review B，2009，80（1）：1-11.

[24]KÖDDERITZSCH D，HERGERT W，TEMMERMAN W M，et al.Exchange interactions in NiO and at the NiO（100）surface[J].Physical Review B，2002，66（6）：1-9.

[25]汪志诚.热力学·统计物理[M].2版.北京：高等教育出版社，1980.WANG Z C.Thermodynamics and Statistical Physics[M].2nd Edition.Beijing：Higher Education Press，1980（in Chinese）.

[26]JAGADEESH M S，SEEHRA M S.Principal magnetic susceptibilities of MnO and their temperature dependence[J].Physical Review B，1981，23（3）：1185-1189.

[27]LINES M E，JONES E D.Antiferromagnetism in the face-centered cubic lattice.II.magnetic properties of MnO[J].Physical Review，1965，139（4A）：1313-1327.