基于群决策的加权动态网络SBM-DEA模型

范建平，张晓杰，吴美琴

山西大学 经济与管理学院，太原 030006

1 引言

传统的数据包络分析方法（Data Envelopment Analysis，DEA）由Charnes和Cooper等[1]于1978年首次提出，是一个线性的非参数模型，可用来评价多投入产生多产出且同质的决策单元（DMU）的相对效率，其中每个决策单元的投入和产出都来源于系统外部。由于它无需设定生产函数和投入产出的权重值，相对其他评价方法具有一定的优势，因此已被广泛应用到各个领域。然而，它在评价时忽略了决策单元内部的运行过程。得到的效率评价结果不仅与实际情况不符，而且还有可能误导评价者。

因此，Charnes和Cooper等[2]首次提出了网络DEA模型，后又有学者在此基础上延伸出不同结构的网络DEA模型，比如Wang等[3]提出了两阶段加法网络DEA模型，并通过测量中国16家主要商业银行的效率证明了模型的可行性，Liu等[4]在此基础上构建了基于非期望产出的两阶段网络DEA模型，高长宏等[5]提出了基于三阶段的网络DEA模型。黄袆等[6]提出了基于链性的关联网络DEA模型，陈凯华等[7]构建了共享投入的关联两阶段生产系统的网络DEA效率测度与分解模型，该模型无需事先主观设定子效率和系统效率的组合关系，而通过事后分解确立二者之间的凸线性组合关系。Kao[8]对网络DEA模型的提出及发展进行了较为详细的综述。

与此同时，跨时期效率即动态效率的测量及其变化也是学者们的关注点之一。Klopp[9]首次提出窗口分析方法来评价决策单元的动态效率，Fӓre等[10]提出基于Malmquist指数的动态效率DEA评价方法，并把效率变化分解成技术进步和技术创新，但是它们都忽略了连续时期间的相互作用。为了进一步探讨连续时期间的相互作用，Fӓre等[11]首次提出一个新的动态DEA方法，且进一步探讨了它的生产前沿面。Park等[12]研究了多个时期的效率集结问题，Sueyoshi等[13]分别讨论了规模收益可变和规模收益不变的动态DEA模型，Tone等[14]建立了基于松弛变量的动态DEA模型，Chen[15]和Nemoto等[16-17]将其应用到生产过程以及电力公司的动态效率评价中。

然而，单纯地考虑系统的内部结构或者动态结构是片面的，因此Keikha Java[18]和Tone等[20]学者提出了动态网络DEA方法。Keikha Java等[18]建立了平行网络结构的动态DEA模型，Kordrostami等[19]将此模型的数据类型延伸为区间型数据。Tone等[20]建立了一般结构的动态网络SBM-DEA模型。动态网络DEA模型可以同时考虑系统的内部网络结构和动态变化，更加符合实际。它在实际中的应用涵盖了高新技术产业[21]、银行业[22-23]、报警系统[24]、公共运输[25]及创新[26]等各个领域。

已有文献在应用动态网络DEA模型时有一个共同点即DMU个数与变量数相当，且由于同时考虑网络结构和动态效应，变量个数要比非动态网络DEA模型大得多。因此当 DMU个数相对变量数小很多时，模型可能不再适用；其次，在应用模型时只是简单地将数据代入模型得到相应的效率值，然后根据效率值来判断有效还是非有效，体现不出评价者的主观态度。然而，如果考虑评价者的主观态度引入预测变量后又可能使得模型的时间变量数增加，相对DMU个数大更多；最后，在已有模型中，子过程和子时期的权重通常是由外界给定[20]或者根据Liang等人提出的合作博弈思想采取平均权重[27]或者以子过程或子时期效率值在综合效率中的比值[21]作为权重。总之，现有的动态网络DEA模型主要存在三方面的问题：一是当DMU个数较少时模型分辨力下降的问题；二是评价时不能体现评价者主观态度的问题，三是子时期和子过程权重的赋值问题。

因此，本文提出了一个基于群决策的加权动态网络SBM-DEA模型。首先提出“过渡期”这一概念，通过态度参数计算每相邻两年之间的最可能值，作为评价者对投入产出变量的主观预测值，接着分别提出平均值法和生物学领域的指数衰减模型来确定子过程和子时期的权重，最后结合群决策思想来解决动态网络DEA模型评价效率时分辨力下降的问题。

2 动态网络SBM-DEA模型

首先，假设有n个决策单元DMUj(j=1,2,…,n)，而且每个决策单元都有K个子过程，其中子过程k的投入变量和产出变量的个数分别用mk和rk表示，子过程k和h之间的相互作用表示为(kh)l，且假设这两个子过程之间的相互作用的数量可记为Lkh种。另假设∈R+(i=1,2,…,mk;j=1,2,…,n;k=1,2,…,K;t=1,2,…,T)表示的子过程k在时刻t的第i个投入；R+(r=1,2,…,rk;j=1,2,…,n;k=1,2,…,K;t=1,2,…,T)表示的子过程k在时刻t的第r个产出，生产过程中产生的非期望产出当作投入处理。1,2,…,n;l=1,2,…,L(kh);t=1,2,…,T)表示的是 DMUtj的子过程k和h在时刻t的相互作用。来自上一时期的产出变量对决策单元产生的影响记为∈ R+(j=1,2,…,n;l=1,2,…,Qk;t=1,2,…,T-1) ；同理，决策单元对下一时期产生的影响则记为∈R+(j=1,2,…,n;l=1,2,…,t=1,2,…,T),其中Qk、分别表示来自上一时期的产出变量对的影响的数量和它对下一时期产出变量的影响的数量。Wt和wk为子时期和子过程权重，且它们都满足因此，可构建第 j0个决策单元的效率评价模型如图1所示。

图1 效率评价模型

3 基于群决策的加权动态网络SBM-DEA模型

3.1 过渡期及其投入产出预测

系统的外部环境因素是随机变化的，评价者的主观态度会随着外部环境的变化而变化，当评价者认为外部环境因素为有利时，持乐观态度，当评价者认为外部环境因素恶化时，会持有悲观态度，当评价者认为外部环境因素的影响不大时，会持中立的态度。然而，评价者通常在评价决策单元的动态效率时，会直接将相应时期的投入产出数据代入模型进行计算，从而得到决策单元的相对效率，这难以体现出评价者的主观态度。为此，本文提出了“过渡期”这一概念，将其定义为相邻两个时期之间的中间时期，并通过态度参数[29]对过渡期的投入产出数据进行了主观预测。

定义1设P为基本单位区间（BUM）函数，满足P:[0,1]→[0,1],P(0)=0，且P(x)为单调函数，Ψ 为非负区间数集，设区间数[aL,aU]∈Ψ ，设a为最可能值，也可称为三元区间数的“重心”，F:Ψ→R+，若满足式（1）：

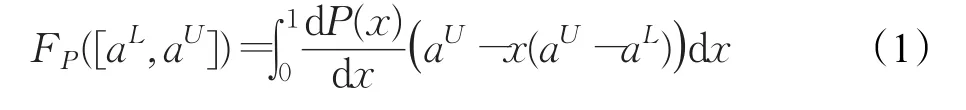
则称F为连续有序加权平均算子，并称基本BUM函数P(x)的态度参数。

同时，由公式（1）可以推导出最可能值公式：

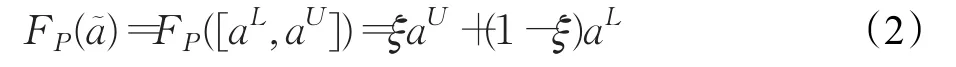
由公式（2）可知，当 ξ=0时，FP(a)=aL，最可能值为区间数的下界；当ξ=1时，FP(a)=aU，最可能值为区间数的上界，当 ξ=0.5时，FP(a)=(aU+aL)/2，最可能值为区间数的中值，因此，当ξ∈[0,0.5]时，评价者持悲观态度，当ξ∈[0.5,1]时，决策者持乐观态度。此处假设当评价者持悲观态度时，态度参数ξ取0.2，当评价者持乐观态度时，态度参数ξ取0.8。

假设要预测决策单元DMUj在第一个过渡期的投首先需要构建一个区间数，其中下界为来自子时期1和2的投入数据的最小值上界为最大值接着代入公式（2）即可求得该区间数据的最可能值，也就是DMUj第一个过渡期的投入预测值。

同理，可以得到其他投入和产出变量在第一个过渡期的悲观预测值和主观预测值分别如表1和表2所示。其中投入变量预测值为产出变量预测值为需注意的是上一时期变量对决策单元的影响来自于已知的子时期1，的值是相同的，前者表示第一个过渡期受上一时期的影响，后者表示子时期1对下一时期的影响。同理，可获得其他“过渡期”的投入产出预测值。

表1 第一个“过渡期”的悲观预测值

表2 第一个“过渡期”的乐观预测值

3.2 基于指数衰减确定子时期权重

不同时刻的权重的变化趋势与生物学和物理学中的指数衰减模型相同，因此，可以通过指数衰减模型[28]来确定不同时刻即各个子时期的权重。

由于本文所涉及的时间类型是离散时间类型，因此设时间集合为Ω=[t1,t2,…,tT]，某一时刻q的权重为wtq，构成集合Wt=[wt1,wt2,…,wtT]，则满足：

其中C0>0,为常数，0<η<1为衰减系数。且wtq满足可以解得是公式（3）可以化为：

特别的，当Ω=[1,,2,…,T]，时，公式（4）可以化为：

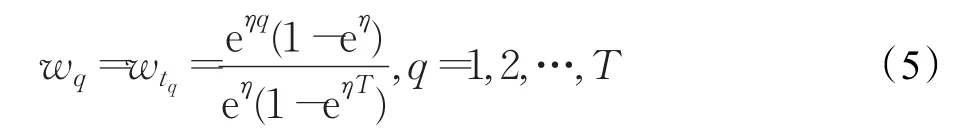
其中，衰减系数的值是评价者根据不同时刻掌握的信息变化情况来确定的。衰减系数越高，说明越靠近最终时刻的信息对最终结果的影响最大，反之越小。而效率的动态评价问题可以当作群决策问题处理，不同时刻的效率值对最终效率值的影响程度不同，而且越靠近最终时刻，影响程度越大，因此问题就转化为如何通过衰减公式（5）确定不同时刻的权重，本文在计算时将衰减系数η的值取为0.5。

3.3 基于群决策的加权DNSBM-DEA模型

由3.1节可知，在已知的投入产出基础上引入过渡期以后，共有(2T-1)组投入产出数据，本文将相邻的u个时间段看作一个评价者，u可以取2或3，且由于相邻时期间隔较短，所以本文取平均值1/u作为相邻子时期的权重，可知评价者共有U个，U=(2T-1)/u。假设各个评价者的权重为w1,w2,…,wd,…,wU，由上可知评价者的权重的关系满足公式（5）。构建加权动态网络SBM-DEA模型如模型（6）所示：

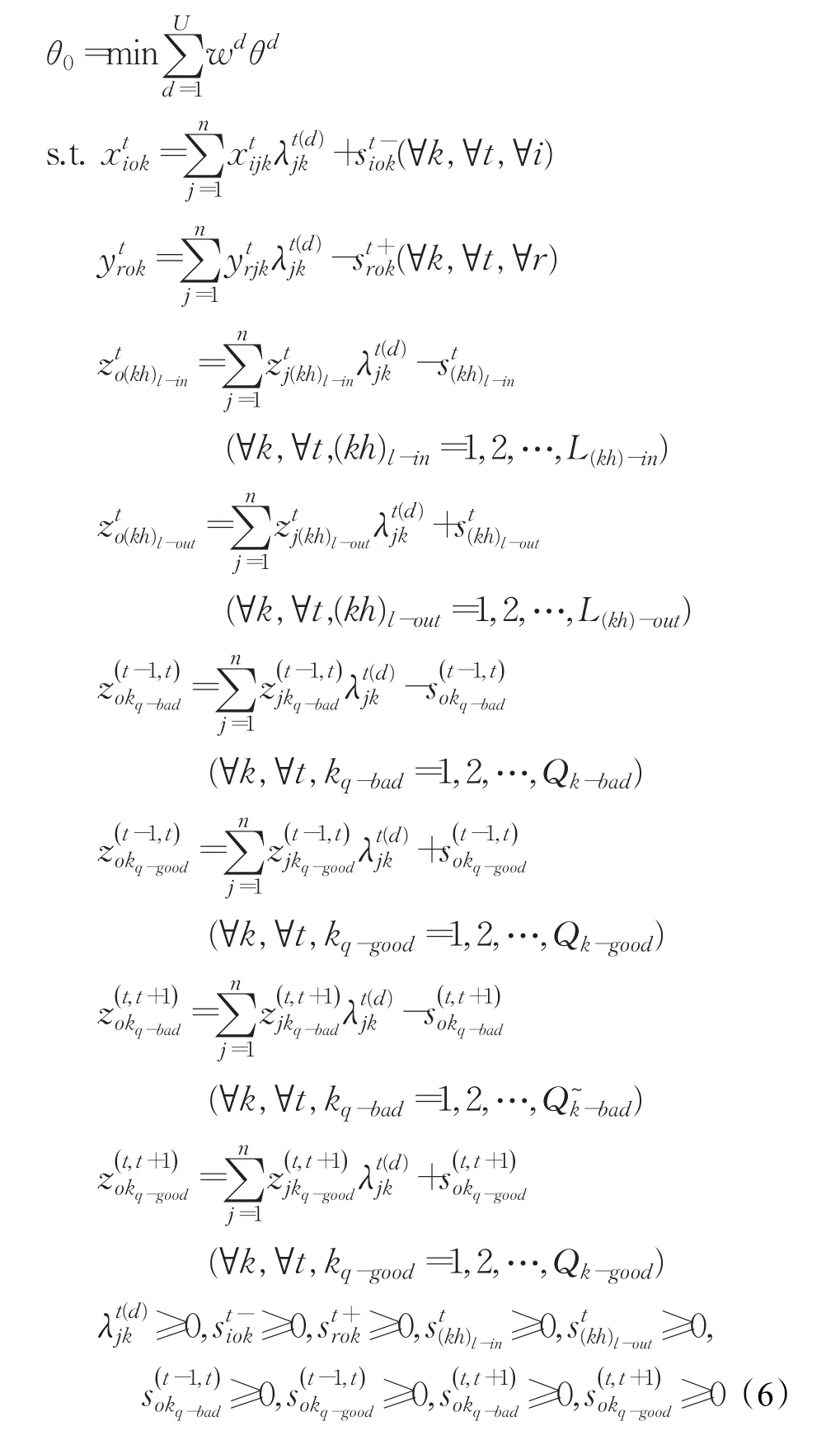
4 模型应用及结果分析

4.1 投入产出及数据预测

2007年银行贷款增长迅速，利差有所扩大，盈利能力大幅提升，不良资产小幅“双降”，风险状况基本稳定，此时，假定评价者认为2008年银行业发展趋势较好，对下一年的发展持乐观态度；2008年到2014年间，受金融危机、欧债危机等不良环境因素的影响，假定评价者认为银行业的发展前景不容乐观，并对下一年的发展持悲观的态度。

本文选取营业成本和利息成本为第一阶段的投入指标，存款为产出指标；第二阶段的投入来源于第一阶段的产出即存款，产出指标包括营业收入、利息收入和不良贷款比率，其中不良贷款比率是非期望产出，当作“投入”处理同时来自上一时期的结转指标采用“上期的不良贷款比率”。数据来源于wind资讯，且已经过GDP平减指数处理。原始的变量描述和引入过渡期后的变量描述如表3所示。

表3 变量的数据描述

由表3可知，各变量的标准差与原始数据几乎相等，甚至比原始数据的标准差小，而均值和中值则变化稍微明显：投入变量的均值和中值均有增加的趋势，产出变量除不良贷款率外都有减小的趋势，这与本文假设的“自2008年到2014年间受外部不良因素的影响评价者对银行的发展持悲观态度”是吻合的。

4.2 模型求解及结果分析

根据上述求解过程，首先从第一个子时期开始，每相邻的3个时期看作一个评价者，代入动态网络DEA模型，便可以得到各个评价者的综合评价值，结果如表4所示。

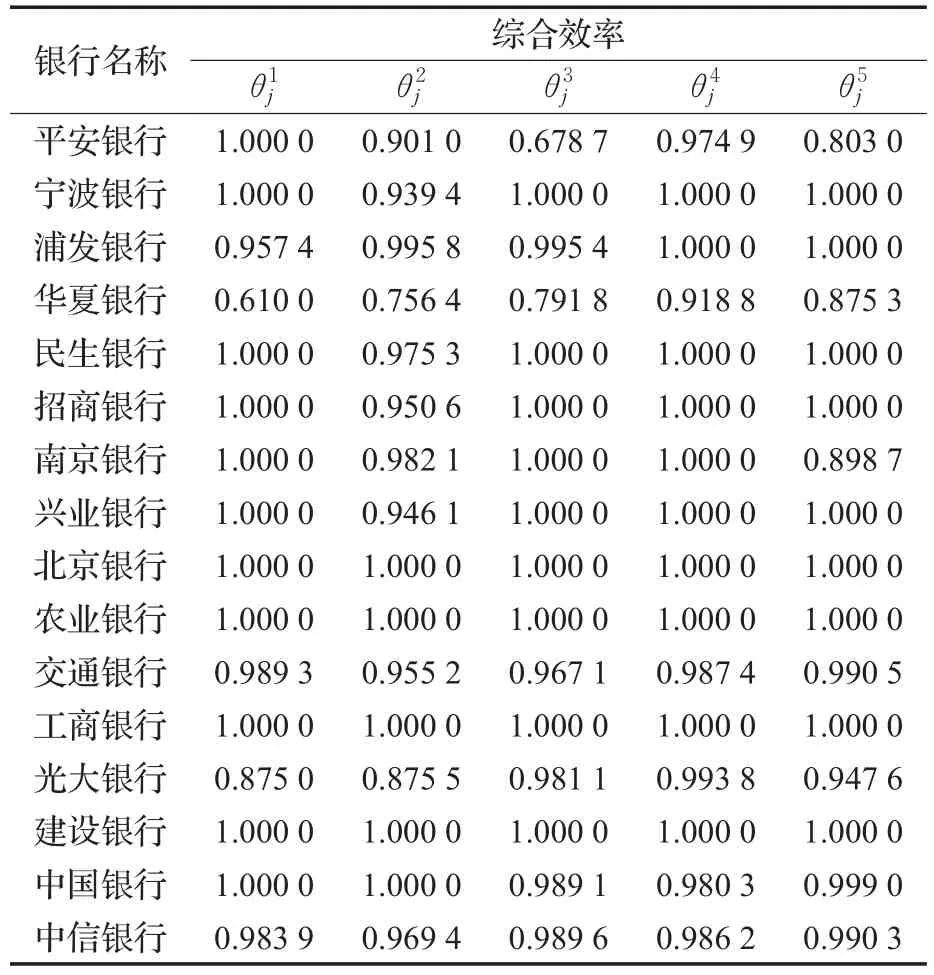
表4 各评价者的综合效率评价值

代入公式（5）求得各个评价者的权重分别是0.06、0.1、0.16、0.27、0.41，最后代入模型（6）便可得16家上市银行的综合效率值和子过程效率分解值，与原始模型的评价结果对比如表5所示。由表5可知，绝大多数决策单元为有效或效率值接近于1。显然与本文提出的模型相比，不仅效率值偏高，而且分辨力明显下降。首先从综合效率评价值看，有效决策单元的个数由一半以上减少到只有4个，而且通过计算标准差可知，原始模型得到的综合效率值的标准差为0.018 1，改进后标准差0.050 1，明显大于0.018 1，说明本文提出的方法解决了上述提到的分辨力下降的问题，证明基于群决策的动态网络SBM-DEA模型适用于评价个数较少且远远小于变量个数的决策单元的相对效率。

表5 中国16家上市银行的效率评价及效率分解

表6 衰减系数对综合效率评价值的影响

其次，从表3变量的数据描述可以看出，考虑评价者的主观态度以后，总体上的投入变量有增加趋势，产出变量有减少趋势，即总体呈悲观态度。从表5可以看出，综合效率评价值与原始模型得到的评价值相比，总体有所降低，因此，可以认为，考虑评价者的主观态度以后，得到的评价值更加客观。此外，前文提到的引入过渡期导致变量增加模型分辨力下降的问题，也通过群决策思想得到了有效解决，从各个决策单元的排名结果也可以看出来。

最后，通过指数衰减模型来确定子时期的权重值，与原始模型的权重确定方法相比较，不仅体现了主观上认为的各时期权重随着时间的递推逐渐减小的看法，而且还具有一定的数学依据，更具有说服力。

4.3 ξ和η对效率值的影响分析

本节分别讨论了态度参数和衰减系数对最终效率值的变化情况，结果如表6所示，根据对表6第1栏的评价值对决策单元进行排名，排名结果如表7所示。

表7 衰减系数变化时DMU的排名变化(ξ=0.2)

由表6可知，当态度参数不变，衰减系数发生变化时，最终效率值会随着衰减系数的变化而变化。先对表6第1列进行分析，发现当态度参数取0.2，衰减系数分别取0.1、0.5和0.8时，各决策单元的排名结果也发生了相应变化，如表7所示。其中，平安银行、浦发银行、华夏银行、光大银行和中信银行的排名均随着衰减系数的增加先前进后退后，说明这些银行在中间时期的发展较好，而前期和后期则相对较差；宁波银行、民生银行交通银行和中国银行的排名均随着衰减系数的增加而退后，说明它们在前期发展较好，而后期则相对较差；招商银行和兴业银行的发展趋势则与宁波银行等正好相反；南京银行的排名结果变化较为明显，且后期明显好于前期的发展；其他银行如北京银行、农业银行和工商银行等则发展较为稳定。同样，当态度参数取0.5和0.8时，也可以得到银行的发展变化情况。

当衰减系数不变，态度参数发生变化时，如表6中的第1列、第4列和第7列所示，可以看出，模型的分辨力依然比原始模型的分辨力要高，且综合效率评价值随着态度参数的变化而变化，说明评价的主观态度影响了决策单元的综合效率评价值，即本文提出的模型可以体现出评价者的主观态度。

5 结语

传统的数据包络分析模型在进行效率评价时，忽略了评价者的主观态度。同时，在实际中应用数据包络分析模型进行效率评价时，如上市银行效率评价、环境测评及创新效率评价等，决策单元的个数往往是固定且有限的，但为了使得到的评价结果更加客观和准确，通常需要考虑决策单元的内部网络结构和多个时期的指标，如此必然会增加投入产出变量的个数，导致变量个数远远大于决策单元的个数，出现模型的分辨力下降，效率值偏高的问题。实例结果表明，本文提出的模型可以有效处理这些问题，并且得到的评价值和排名结果都比较理想。

然而，本文是基于规模报酬不变的条件下进行研究的，规模报酬可变的情形则还有待进一步探讨。

[1]Charnes A，Cooper W W，Rhodes E.Measuring the efficiency of decision making units[J].European Journal of Operational Research，1978，2（6）：429-444.

[2]Charnes A，Cooper W W，Golany B，et al.Two-phase data envelopment analysis approaches to policy evaluation and management of army recruiting activities：Tradeoffs between joint services and army advertising，Research Report CCS#532[R].Center for Cybernetic Studies，University of Texas-Austin，Austin，TX，1986.

[3]Wang K，Huang W，Wu J，et al.Efficiency measures of the Chinese commercial banking system using an additive two-stage DEA[J].Omega，2014，44（2）：5-20.

[4]Liu Wenbin，Zhou Zhongbao，Two-stage DEA models with undesirable input-intermediate-outputs[J].Omega，2015，56（3）：74-84.

[5]高长宏，邹杨波.基于三阶段网络DEA模型的中国上市商业银行效率研究[J].金融经济，2014，20（34）：89-91.

[6]黄袆，葛虹，冯英浚.基于链性系统的关联网络DEA模型：以我国14家商业银行为例[J].系统工程理论与实践，2009，29（5）：106-114.

[7]陈凯华，官建.共享投入型关联两阶段生产系统的网络DEA效率测度与分解[J].系统工程理论与实践，2011，3（7）：1211-1219.

[8]Kao C.Network data envelopment analysis：A review[J].European Journal of Operation Research，2014，239（1）：1-16.

[9]Klopp G A.The analysis of the efficiency of production system with multiple inputs and outputs[D].University of Illinois，Industrial and System Engineering College，Chicago，1985.

[10]Fӓre R，Grosskopf S，Norris S，et al.Productivity growth，technical progress and efficiency change in industrialized countries[J].American Economic Review，1994，84（1）：66-83.

[11]Fӓre R，Grosskopf S.Inter-temporal production Frontiers：With dynamic DEA models[J].Norwell：Kluwer，1996.

[12]Park K S，Park K.Measurement of multi period aggregative efficiency[J].European Journal of Operational Research，2009，193（2）：567-580.

[13]Sueyoshi T，Sekitani K.Returns to scale in dynamic DEA[J].European Journal of Operational Research，2005，161（2）：536-544.

[14]Tone K.Dynamic DEA：A slacks-based measure approach[J].Omega，2010，38（10）：145-156.

[15]Chen C M.network-DEA：A model with new efficiency measures to incorporate the dynamic effect in production networks[J].European Journal of Operational Research，2009，194（3）：687-699.

[16]Nemoto J，Goto M.Dynamic data envelopment analysis modeling intertemporal behavior of a firm in the presence of productive inefficiencies[J].Economic Letters，1999，64（1）：51-56.

[17]Nemoto J，Goto M.Measuring dynamic efficiency in production：An application of data envelopment analysis to Japanese electric utilities[J].Journal of Productivity Analysis，2003，19（2/3）：191-210.

[18]Keikha Javan S，Rostamy Malkhalifeh M.Non radial modelofdynamicDEA with theparallelnetwork structure[J].International Journal of Data Envelopment Analysis，2013，1（2）：107-118.

[19]Kordrostami S，Azmayandeh O，Bakhod Z，et al.The new model in interval dynamic network DEA for parallelproduction system：An illustration with Iranian banks[J].Indian Journal of Science and Technology，2013，6（1）：44-53.

[20]Tone K，Tsutsui M.Dynamic DEA with network structure：A slacks-based measure approach[J].Omega，2014，42（1）：124-131.

[21]Bai Xuejie，Yan Wenkai，Chiu Y H.Performance evaluation of Chinese Hi-tech zones in the post financial crisis era-Analysis based on the dynamic network SBM model[J].China Economic Review，2015，34（4）：122-134.

[22]Avkiran N K.An illustration of dynamic network DEA in commercial bank including robustness tests[J].Omega，2015，55：141-150.

[23]Zha Yong，Liang Nannan，Wu Maoguo，et al.Efficiency evaluation of banks in China：A dynamic two-stage slacks-based measure approach[J].Omega，2016，60（12）：60-72.

[24]Herrera-Restrepo O，Triantis K，Trainor J，et al.A multiperspectivedynamicnetwork performanceefficiency measurementofanevacuation：A dynamicnetwork-DEA approach[J].Omega，2016，60（4）：45-59.

[25]Yu M M，Chen L H，Bo H.Dynamic performance assessment of bus transit with the multi-activity network structure[J].Omega，2016，60（6）：15-25.

[26]Kou Mingting，Chen Kaihua，Wang S，et al.Measuring efficiencies of multi-period and multi-division systems associated with DEA：An application to OECD countries’nationalinnovation systems[J].ExpertSystemswith Applications，2016，46（10）：494-510.

[27]陈磊，王应明.基于松弛变量方法的动态网络松弛效率测度及分解[J].系统科学与数学，2015，35（3）：361-370.

[28]毛军军，姚登宝，陈华友，等.基于时序模糊软集的群决策方法[J].系统工程理论与实践，2014，34（1）：182-189.

[29]Yager R R.OWA aggregation operator：A continuous interval argument with application to decision making[J].IEEE Transactions on Systems，Man and Cybernetics：Part B Cybernetics，2004，34（5）：1952-1963.