带碳排放约束的闭环供应链企业合作减排决策
2018-06-26汪传旭
李 辉,汪传旭
上海海事大学 经济管理学院,上海 201306
1 引言
近年来,节能和环保问题已经得到世界各主要国家和国际组织的重视,当前社会解决节能环保问题最直接的方法是降低碳排放水平,而废旧产品进行回收再制造不仅能够降低产品的制造成本,提高参与企业的获利水平,而且能够减少碳排放量,起到减少环境污染、节约资源的作用。因此,在低碳背景下研究闭环供应链中制造商和零售商不同的合作减排模式对减排率、回收率和利润的影响,将为企业在低碳环境下制定减排决策和回收决策以及为政府如何对相关企业进行奖惩以实现最优的减排效果提供一定的借鉴意义。
与本文相关的研究主要体现为低碳闭环供应链和供应链企业合作减排的研究。在低碳闭环供应链研究方面,Olugu和Wong指出闭环供应链管理的原则之一是减少碳排放[1]。Kannan等在确定型逆向供应链的企业节点选址问题中采用碳足迹的方法进行研究[2]。Krikke等研究了碳足迹对闭环供应链网络结构的影响[3]。Chaabane等基于对闭环供应链各节点碳排放量的计算,指出企业通过有效的碳管理机制能够实现可持续化目标[4]。Subramanian等研究了基于单一产品在回收不确定情况下,分析了回收率对闭环供应链碳排放的影响[5]。在文献[5]的基础上,Paksoy分析了市场需求、回收率、运量、排放率等因素对多产品闭环供应链运输过程中碳排放成本的影响[6]。随着研究的不深入,部分学者在低碳闭环供应链的研究中考虑政府政策干涉,Ma等考虑了政府对消费者进行消费补贴情况下双渠道闭环供应链的网络规划问题[7]。Wang等以碳排放为约束,构建了制造/再制造闭环供应链的多目标混合线性规划模型,并研究了单个、整合目标模型的成本和环境效率[8]。Zhang等考虑了两种强制性碳排放政策,并分析了它们对网络均衡的影响[9]。Fareeduddin等基于碳的优化模型提出了一个闭环供应链设计和物流业务的监管政策[10]。高举红等考虑了碳排和多种不确定因素的情景下,建立了非线性混合整数规划模型,分析了碳补贴强度的改变对闭环供应链网络规划的影响[11]。文献[2-11]只研究了碳足迹对闭环供应链网络结构的影响,没有考虑闭环供应链中的决策问题。针对这一问题,高举红等在考虑回收质量的回收定价策略下,构建了4种回收情境来研究不同回收模式和市场主导力量对闭环供应链碳排放和收益的影响[12]。聂佳佳等在碳排放约束下,对零售商负责回收闭环供应链进行了研究[13]。郭成恒等研究了基于对第三方补贴、对制造商补贴、对制造商征收碳税、对制造商征收碳税同时对第三方实施补贴的不同奖惩机制下闭环供应链的分散决策[14]。在供应链企业合作减排的研究方面,Poyago-Theotoky分析了供应链企业减排投资过程中技术合作溢出问题[15]。Benjaafar等将碳足迹引入供应链管理中,分析如何通供应链企业合作减少碳排放的问题[16]。Zhou等分析了制造商和零售商既不分担减排成本又不合作宣传、只合作宣传不分担减排成本、只分担减排成本不合作宣传以及既分担减排成本又合作宣传4种模式对供应链利润的影响[17]。谢鑫鹏和赵道致分析了供应链企业在3种不同合作情况下的减排效果和利润,探讨了在减排过程中企业的相互作用、碳交易价格对减排效果的影响以及社会福利的比较等问题[18]。王芹鹏和赵道致比较了不合作、成本分担契约以及合作3个契约对供应链成员的影响[19]。赵道致等借助微分博弈研究由单个制造商与两个零售商组成的供应链系统中长期联合减排和低碳宣传的问题[20]。李友东等考虑了零供双方基于分享减排所增收益与分担减排投资成本两种契约进行合作减排,比较了不同契约形式下最优减排水平、最优分成比例以及最优利润值[21]。
综上所述,现有研究主要呈现如下特点:低碳闭环供应链的研究主要侧重于网络结构优化问题,对于供应链博弈决策问题研究较少。供应链企业合作减排的研究较少,现有的研究中也仅仅局限于一般正向供应链背景,没有结合闭环供应链进行研究,也很少考虑碳排放约束对供应链决策的影响。因此,本文主要考虑闭环供应链中零售商与制造商采用减排所增利润分享和减排成本分担两种合作减排模式,构建闭环供应链Stackelberg博弈决策模型,并对不同合作减排下的决策效果进行比较分析,同时分析闭环供应链回收价格和碳排放约束对闭环供应链决策的影响。
2 基本假设
为了研究方便做如下假设:
(1)参照文献[22],假设制造商的减排投资成本为其中λ为实施碳减排投入后制造商的减排率,0<λ<1,u为制造商的减排成本系数,u>0。
(2)消费者愿意为低碳产品支付更高的价格[23],最终提高了低碳产品的市场需求。因此,参照文献[13]假设市场需求D()λ=α-γp+βλ,其中α为市场潜在需求,p为新产品的零售价格,且假设p在减排前后没有发生变化,β为产品减排率对需求的影响因子,且α>γp,β>0。
(3)τ为回收率,表示当期产品在再制造品所占的比例,0<τ<1。参照文献[24-25],τ=I cL,其中 I表示对回收活动的投资,cL表示废旧品回收活动的规模,是足够大的变量。因此,制造商的回收成本为C()τ=I+bτD(λ)=cLτ2+bτD(λ)。
(4)参照文献[26],为了节约回收成本,制造商以转移价格b直接从消费者处回收废旧产品,b>0。
(5)cm为制造商制造新产品的单位成本,cm>0,cr为再制造品的单位成本,cr>0,本文在研究中遵循再制造的经济前提,假设通过回收废旧产品进行再制造要比从无到有生产新产品便宜,即cm>cr。通过再制造节约的单位成本为δ=cm-cr,制造商的平均单位成本c=cm(1-τ)+crτ,为了使再制造具有经济效益,假设δ>b。
(6)参照文献[13],e为制造商使用原材料生产单位产品过程中产生的碳排放量,θ为制造商通过废旧产品回收再制造的单位产品产生的碳排放量同原产品碳排放量的比值θ(0<θ<1),θ越大表示产品回收再制造对减少碳排放量的作用越小。即再制造产品产生的碳排放量为θe,再制造的减排效用为1-θ。g为单位产品在生命周期内的平均碳排放量,g=e( )1-τ+θτ。
(7)a为政府制定的制造商生产单位产品的碳排放上限,k为政府制定的制造商单位产品碳排放量奖惩系数,k>0。
图1为制造商负责回收的闭环供应链系统。

图1 制造商负责回收的闭环供应链
3 模型建立与分析
本文考虑作为市场主导的零售商与制造商的两种合作减排模式。为了便于分析两种合作减排方式对闭环供应链成员利润的影响,首先以零售商不参与合作减排作为基准。
3.1 零售商不参与合作减排模式(D)
首先以零售商不参与合作减排模式为基准,由于新产品的价格为常量,需求随着制造商的减排水平单调递增,制造商的减排水平越高,零售商的利润越多。因此,在该模式下,制造商和零售商的利润函数分别为:
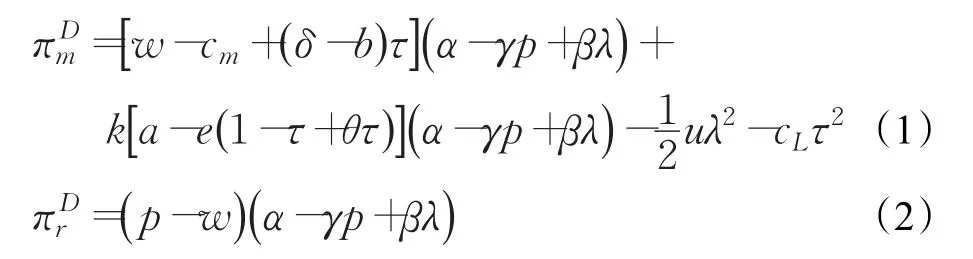
为了简化下面的计算过程,令制造商单位销售收益F=w-cm,制造商单位回收收益G=δ-b,零售商单位销售收益H=p-w,固有市场规模N=α-γp。因此,制造商和零售商的利润函数可以改写为:

联立,得到模式(D)制造商的最优减排率和最优回收率,由制造商利润函数的Hessian矩阵可知,若Hessian矩阵的顺序主子式2cLu-Δ2β2>0。此时,制造商的利润函数是关于减排率λ和回收率τ的联合凹函数。
联立,得到模式(D)制造商的最优减排率和最优回收率:


其中 Δ=G+ek(1 -θ)],ω=F+(a -e) k。
为了保证0<λD*<1且0<τD*<1,则需同时满足:ω>0,u>ωβ和将式(5)和式(6)代入式(1)和式(2)得到模式(D)制造商的最优利润和零售商的最优利润:
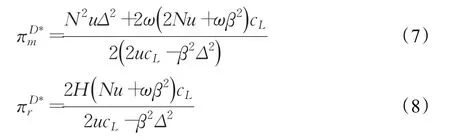
因为零售商的利润函数是减排率的增函数,所以制造商愿意和制造商合作减排提高减排水平,实现双方利润的增加。
3.2 减排所增利润分享合作减排模型(S)
在该模式下,零售商和制造商分别以ϕ和(1-ϕ)分享零售商低碳产品需求增加部分所获得的增值利润。因此,制造商和零售商的利润函数分别为:
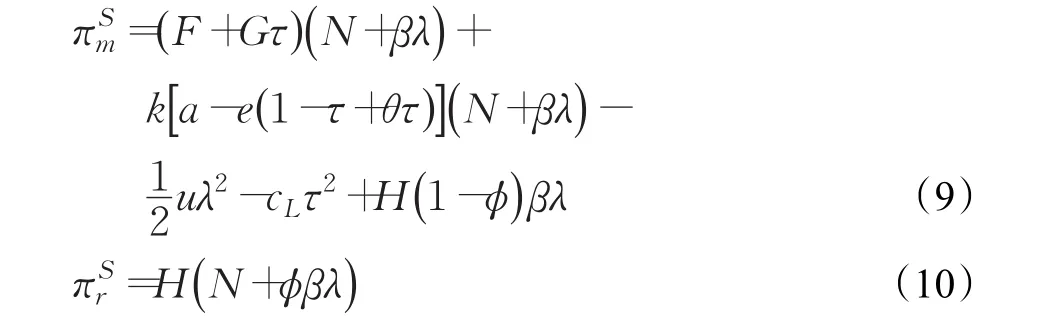
零售商作为Stackelberg博弈的主导者,首先确定减排所增利润分享比例ϕ,使自身利润最大化。在已知零售商的减排所增利润分享比例后,制造商确定减排率λ和回收率τ。根据逆向归纳求解法,由制造商利润函数πSm的Hessian矩阵可知,若Hessian矩阵的顺序主子式时,此时,制造商的利润函数是关于减排率λ和回收率τ的联合凹函数。
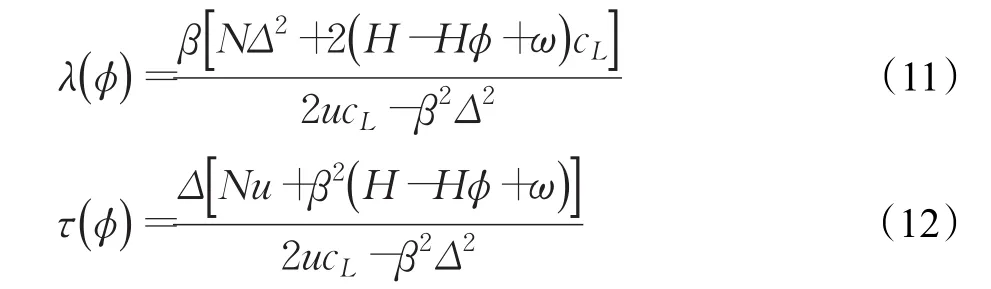
将式(11)和式(12)代入式(10)得到模式(C)零售商的最优利润:

零售商基于自身的利润最大化决定最优的分享比例ϕ*。由于零售商利润函数(ϕ)是关于分享比例ϕ的凹函数。得到零售商的最优分享比例:

为了保证0<ϕ*<1,则需同时满足:H>ω和cL>
将式(13)代入式(11)和式(12),进一步得到模式(C)的最优减排率和最优回收率,即
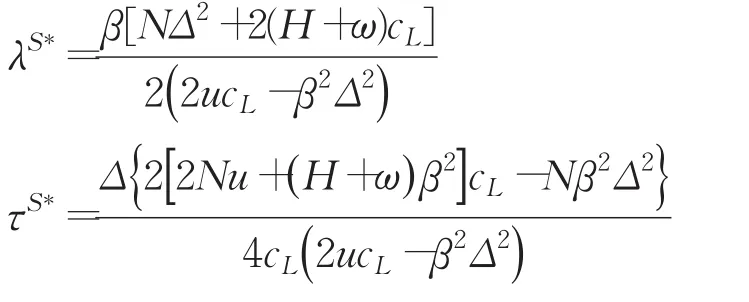
为了保证0<λS*<1且0<τS*<1,则需同时满足:

进一步得到模式(S)制造商和零售商的最优利润:
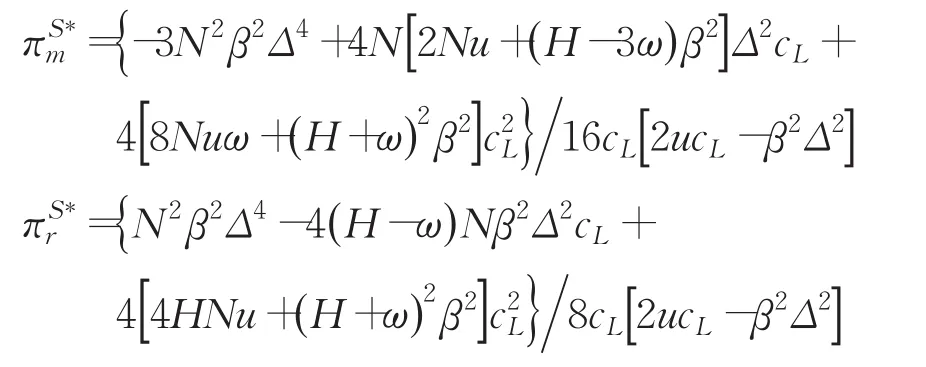
3.3 减排成本分担合作减排模式(C)
在该模式下,零售商以百分比ψ分担制造商的减排成本,那么制造商只需承担1-ψ的减排成本。因此,制造商和零售商的利润函数分别为:
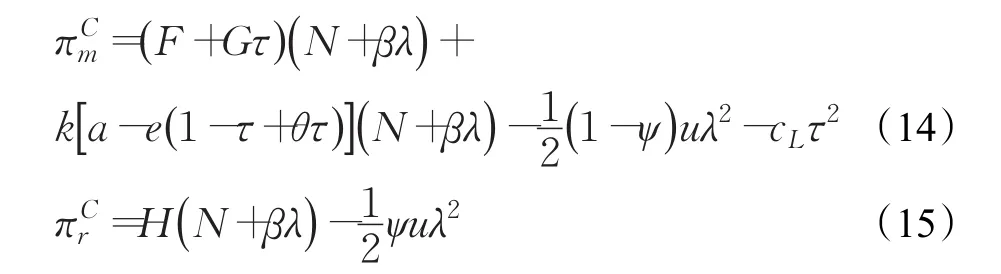
零售商作为Stackelberg博弈的主导者,首先确定减排成本分担比例ψ,使自身利润最大化。在已知零售商对减排成本所分担的比例后,制造商确定减排率λ和回收率τ。根据逆向归纳求解法,由制造商利润函数πCm的Hessian矩阵可知,若Hessian矩阵的顺序主子式此时,制造商的利润函数是关于减排率λ和回收率τ的联合凹函数。
联立,得到模式(C)制造商的最优减排率和最优回收率:

将式(16)和式(17)代入式(15)得到模式(C)零售商的最优利润:
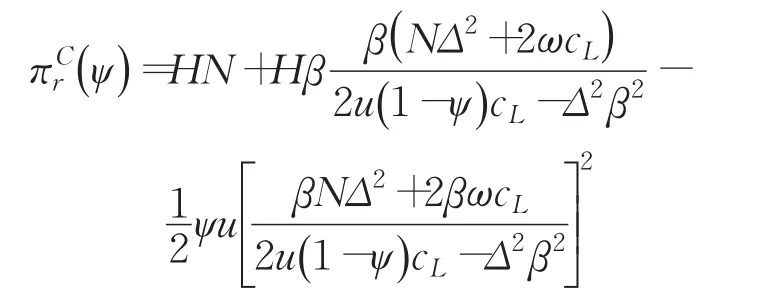
零售商基于自身的利润最大化决定最优的分担比例ψ*。由于,零售商利润函数(ψ)是关于分担比例ψ的凹函数。令得到零售商的最优分担比例:
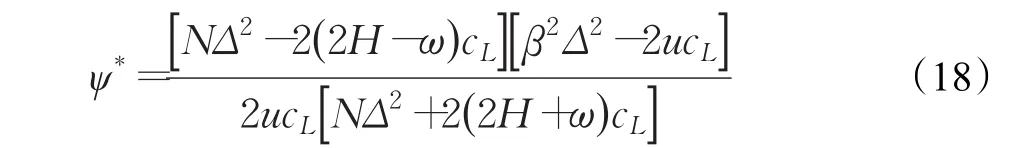
为了保证0<ψ*<1,则需满足:

将式(18)代入式(16)和式(17),进一步得到模式(C)的最优减排率和最优回收率,即

为了保证0<λS*<1且0<τS*<1,则需同时满足:
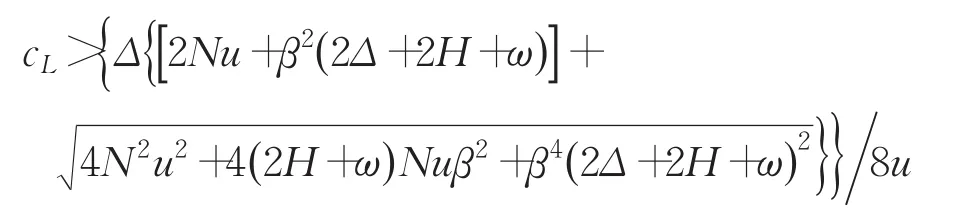
进一步得到模式(C)制造商和零售商的最优利润:

4 3种模式决策结果的比较与分析
为了方便进一步证明和计算,统一取u

4.1 减排率、回收率、制造商利润和零售商利润的比较与分析
定理1 3种模式下减排率和回收率的关系分别如下:
(1)λC*>λS*>λD*;(2)τC*>τS*>τD*。
证明
λS*-λD*即 λS*-λD*,于是得证。

于是得证。
定理1表明:两种合作减排模式均能实现制造商减排水平和回收水平的提高,减排成本分担合作减排使得制造商的减排和回收更彻底,均高于减排所增利润分享合作减排下的减排水平和回收水平。
定理2 3种模式下制造商和零售利润的关系分别如下:情形1(1)当(2)当 H>( )2+1 ω时:
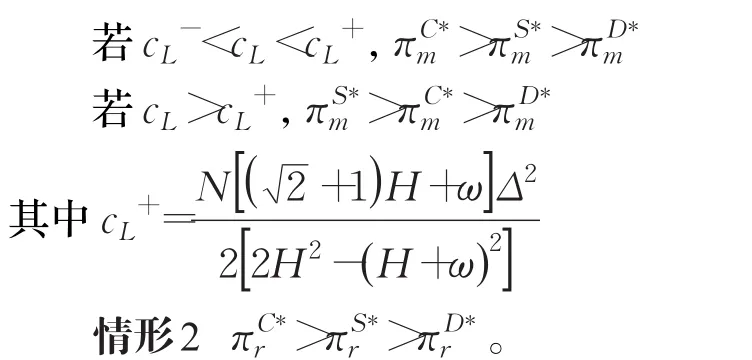
证明(情形1)
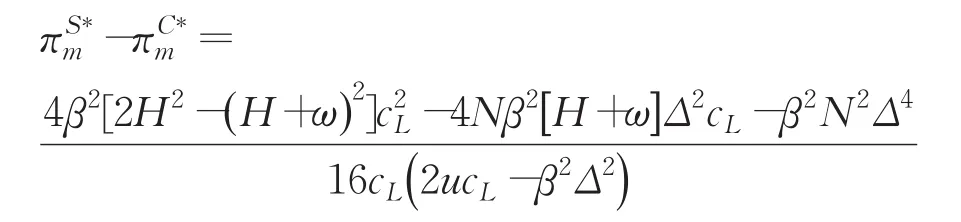
当ω 当H>()+1 ω时,若 在cL>cL-条件下,有即同理可得于是得证。 证明(情形2) 于是得证。 定理2表明:两种合作减排模式均能显示制造商和零售商的利润增加,减排成本分担合作减排下的零售商利润均大于减排所增利润分享合作减排下的零售商利润,而两种合作减排模型的制造商利润大小关系受到零售商单位销售收益和制造商回收活动投入成本大小的影响。当 ω 定理3 3种模式下的减排率和回收率与回收价格成本反比,分享比例与其成反比,分但比例与其成正比。 证明;于是得证。 定理3表明:制造商提高回收价格,降低制造商单位回收废旧产品收益,不利于制造商提高碳减排和废旧产品回收的积极性同时零售商与制造商减排所增利润分享比例降低,减排成本分担比例提高。 定理4 3种模式下的减排率和回收率与单位产品碳排放上限成正比,利润分享比例与其成正比,成本分担比例与其成反比。 证明于是得证。 定理4表明:政府提高制造商生产单位产品的碳排放上限,制造商单位产品的减排压力降低,有利于减排水平和回收水平提高,同时利润分享比例提高,成本分担比例降低。 定理5 3种模式下的减排率和回收率与减排率对需求的影响因子成正比,利润分享比例不受其影响,成本分担比例与其成反比。 证明于是得证。 定理5表明:消费者的环境保护意识提高,愿意为低碳产品支付更高的价格,提升制造商对碳减排和废旧产品回收的积极性。同时,零售商对制造商提高减排所增利润分享比例,而降低减排成本分担比例。 定理6 3种模式下的减排率和回收率与碳排放量的比值成反比,利润分享比例与其成反比,成本分担比例与其成正比。 证明于是得证。 定理6表明:减排技术和再制造技术的进步,提高再制造的减排效用,导致制造商的减排水平和回收水平随之上升。同时,零售商对制造商降低减排所增利润分享比例,而提高减排成本分担比例。 为了分析制造商和零售商的定价、政府奖惩系数、碳减排对需求的影响因子和碳排放量比值对制造商和零售商利润的影响,假设市场潜在需求为α=300,制造商制造新产品的单位成本为cm=40,再制造品的单位成本为cr=20,则再制造节约的单位成本δ=20,废旧品回收活动的规模为cL=6 000,制造单位新产品产生的碳排放量为e=12,制造商的减排成本系数为u=650,消费者对零售价格的敏感系数为γ=1,产品减排率对需求的影响因子为β=3,再制造单位产品的碳排放量和制造单位新产品的碳排放量比值为θ=0.6。可以认为[cL-,cL+]为制造商回收废旧产品活动的理想投入成本的理想区间,反之,[cL+,+∞]为制造商回收废旧产品活动投入成本的不理想区间。 设定制造商支付消费者的不同回收价格,得到回收价格b的变化对上述3种模式制造商和零售商利润的影响,如表1所示。 表1 参数b的变化对3种模式制造商和零售商利润的影响 表1表明:制造商提高支付给消费者的回收价格,降低了减排水平和回收水平,引起单位产品在生命周期内的平均碳排放量增加和需求总量的减少,最终导致利润都减少;制造商利润减少幅度比零售商利润减少幅度明显。制造商支付给消费者的回收价格b在[5,15]内变化时,没有改变零售商单位收益利润的取值范围,因此减排成本分担合作减排的制造商和零售商利润总是最大,其次是减排所增利润分享合作减排的,最小是零售商不参与合作减排的。 选取政府制定的制造商生产单位产品碳排放上限的不同数值,得到单位产品碳排放上限a的变化对上述3种模式下制造商和零售商利润的影响,如表2所示。 表2 参数a的变化对3种模式制造商和零售商利润的影响 表2表明:政府提高制造商生产单位产品的碳排放上限,提升减排水平和回收水平,降低单位产品在生命周期内的平均碳排放量,提高需求总量,以至制造商利润和零售商利润均增加。除此之外,政府制定的制造商生产单位产品碳排放上限a在[3,5]内变化时,零售商单位销售收益H 在[(2+1)ω,+∞]内变化,且制造商回收活动的投资cL∈[cL+,+∞],制造商对废旧产品回收活动投入过大,并根据定理4可知,零售商对制造商提供较大的碳减排成本分担比例也抵消不了回收活动投入过大带来的消极作用,因此减排成本分担合作减排的制造商利润小于碳减排所增利润分享合作减排的制造商利润;反之单位产品碳排放上限a在[6,8]内变化时,零售商单位销售收益H在[(2+1)ω,+∞]内变化,且制造商回收活动的投入成本cL∈[cL-,cL+],制造商对废旧产品回活动投入适中,并根据定理4可知,虽然此时零售商对制造商提供的碳减排成本分担比例较小,但是依然能够让制造商有利可图,因此减排成本分担合作减排的制造商利润大于碳减排所增利润分享合作减排的制造商利润;单位产品碳排放上限a在[9,12]内变化时,零售商单位销售收益H 在[ω,(2+1)ω]内变化,此时减排成本分担合作减排的制造商利润大于碳减排所增利润分享合作减排的制造商利润。总之,减排成本分担合作减排的制造商利润和碳减排所增利润分享合作减排的制造商利润均大于零售商不参与合作减排模式下零售商的利润。 选取政府制定的单位产品碳排放量奖惩系数的不同数值,得到奖惩系数k的变化对上述3种模式减排率、回收率、制造商和零售商利润的影响,如表3所示。 表3表明:政府通过提高制造商单位产品碳排放量奖惩系数,鼓励制造商提高废旧产品回收量,减少单位产品在生命周期内的平均碳排放量增加和需求总量,同时降低了减排水平,导致制造商利润和零售商利润降低;而碳减排成本分担比例随之增加,减排所增利润分享比例随之减少。此外,当k∈[1,4]时,零售商单位销售收益 H∈[ω,(2+1)ω];k∈[5,10]时,虽然零售商单位销售收益H∈[(2+1)ω,+∞],但是制造商回收活动的投入成本cL∈[cL-,cL+],导致减排成本分担合作减排的制造商利润总大于碳减排所增利润分享合作减排的制造商利润,两种合作减排模式下制造商的利润均大于制造商独立减排模式下制造商的利润。 改变产品减排率对需求的影响因子β,以及废旧产品回收再制造的单位产品产生的碳排放量同原产品碳排放量的比值θ,得到β和θ的变化对上述三种模式制造商和零售商利润的影响,如图2~7所示。 图2~7表明:无论哪种模式的制造商利润和零售商利润都随着减排对需求的影响因子增大,再制造的减排效用提高而增加。在两种因素的同时作用下,再制造的减排效用对制造商利润的影响大于减排对需求的影响因子的影响;随着减排对需求的影响因子增大,再制造的减排效用对零售商利润的影响越明显。 表3 参数k的变化对3种模决策结果,制造商和零售商利润的影响 图2 参数β和θ对的影响 图3 参数β和θ对的影响 图4 参数β和θ对的影响 图5 参数β和θ对的影响 图6 参数β和θ对的影响 图7 参数β和θ对的影响 本文考虑碳排放约束下制造商负责回收,零售商与制造商分享减排所增利润和分担减排成本两种方式参与合作减排,研究闭环供应链的回收决策和减排决策,分析了闭环供应链回收价格、单位产品碳排放上限、政府奖惩系数、减排对需求的影响因子和废旧产品回收再制造的单位产品产生的碳排放量同原产品碳排放量的比值对回收策略、减排策略和成员利润的影响,并将零售商不参与减排、减排所增利润分享合作减排和减排成本分担合作减排3种模式进行了比较分析。结果表明:(1)减排成本分担合作减排时的减排水平和回收水平最高,其次是减排所增利润分享合作减排,最后是零售商不参与减排。(2)当或当 H>( )2+1 ω且cL- 本文所假设的批发价格、零售价格和回收价格均为常量,在今后的研究中会考虑闭环供应链各成员的定价决策。另外,本文所假设的需求是依赖回收率和减排率的确定性需求,在实际中需求更倾向于随机需求,因此考虑不确定需求下闭环供应链制造商和零售商联合减排策略和制造商回收策略的影响将是今后进一步研究的问题。 [1]Olugu E U,Wong K Y.An expert fuzzy rule-based system for closed-loop supply chain performance assess-ment in the automotive industry[J].Expert Systems with Applications,2012,39(1):375-384. [2]Kannan D,Diabat A,Alrefaei M,et al.A carbon footprint based reverse logistics network design mode[J].Resources,Conservation and Recycling,2012,67:75-79. [3]Krikke H.Impact of closed-loop network configurations on carbon footprints:A case study in copiers[J].Resources,Conservation and Recycling,2011,55(12):1196-1205. [4]Chaabane A,Ramudhin A,Paquet M.Design of sustainable supply chains under the emission trading scheme[J].International Journal of Production Economics,2012,135(1):37-49. [5]Subramanian P,Ramkumar N,Narendran T T,et al.PRISM:Priority based simulated annealing for a closed loop supply chain network design problem[J].Applied Soft Computing,2013,13(2):1121-1135. [6]Paksoy T,Bektas T,Ozceylan E.Operational and environmental performance measures in a multi-product closedloop supply chain[J].Transportation Research Part E:Logistics and Transportation Review,2011,47(4):532-546. [7]Ma W M,Zhao Z,Ke H.Dual-channel closed-loop supply chain with government consumption subsidy[J].European Journal of Operational Research,2013,226(2):221-227. [8]Wang Y,Lu T,Zhang C.Integrated logistics network design in hybrid manufacturing/remanufacturing system under low-carbon restriction[C]//Proceedings of 2nd International Conference on Logistics,Informatics and Service Science(LISS 2012),2012. [9]Zhang G T,Zhong Y G,Sun H,et al.Multi-period closedloop supply chain network equilibrium with carbon emission constraints[J].Resources Conservation&Recycling,2015,104:354-365. [10]Fareeduddin M,Hassan A,Syed M N,et al.The impact of carbon policies on closed-loop supply chain network design[J].Procedia Cirp,2014,26:335-340. [11]高举红,王瑞,王海燕.碳补贴政策下闭环供应链网络优化[J].计算机集成制造系统,2015,21(11):3033-3040. [12]高举红,侯丽婷,韩红帅,等.考虑碳排放的闭环供应链收益波动分析[J].计算机集成制造系统,2014,20(8):2008-2017. [13]聂佳佳,王拓,赵映雪,等.碳排放约束下再制造闭环供应链回收策略[J].管理工程学报,2015,29(3):249-256. [14]郭成恒,丁雪峰.考虑碳排放差异的闭环供应链奖惩机制与碳减排策略[J].统计与决策,2015,409(13):54-57. [15]Poyago-Theotoky J A.The organization of R&D and environmental policy[J].Journal of Economic Behavior&Organization,2007,62(1):63-75. [16]Benjaafar S,Li Yanzhi,Daskin M.Carbon footprint and the management of supply chains:Insights from simple models[J].IEEE Transactions on Automation Science and Engineering,2013,10(1):99-116. [17]Zhou Yanju,Bao Maojing,Chen Xiaohong,et al.Co-op advertising and emission reduction cost sharing contracts and coordination in low-carbon supply chain based on fairness concerns[J].Journal of Cleaner Production,2016,133:402-413. [18]谢鑫鹏,赵道致.低碳供应链企业减排合作策略研究[J].管理科学,2013,26(3):108-119. [19]王芹鹏,赵道致.两级供应链减排与促销的合作策略[J].控制与决策,2014,29(2):307-314. [20]赵道致,徐春秋,王芹鹏.考虑零售商竞争的联合减排与低碳宣传微分对策[J].控制与决策,2014,29(10):1809-1815. [21]李友东,谢鑫鹏,营刚.两种分成契约下供应链企业合作减排决策机制研究[J].中国管理科学,2016,24(3):61-70. [22]Jones R,Mendelson H.Information goods vs.industrial goods:Coststructure and competition[J].Management Science,2011,57(1):164-176. [23]Liu Z G,Anderson T D,Cruz J M.Consumer environmental awareness and competition in two stage supply chains[J].European Journal of Operational Research,2012,218:602-613. [24]Savaskan R C,Hattacharya S,Wassenhove L V.Closeloop supply chain models with product remanufacturing[J].Management Science,2004,50(2):239-252. [25]Taylor T A.Supply chain coordination under channel re-bates with sales effort effects[J].Management Science,2002,48(8):992-1007. [26]Gao J,Han H,Hou L,et al.Pricing and effort decisions in a closed-loop supply chain under different channel power structures[J].Journal of Cleaner Production,2015,112:2043-2057.
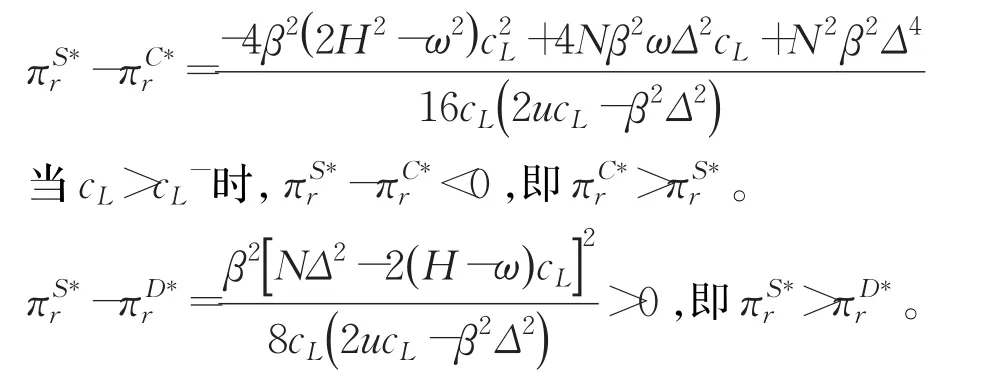
4.2 参数对3种模式决策结果的影响
5 算例分析
5.1 制造商和零售商定价的变化对各种模式下成员利润的影响

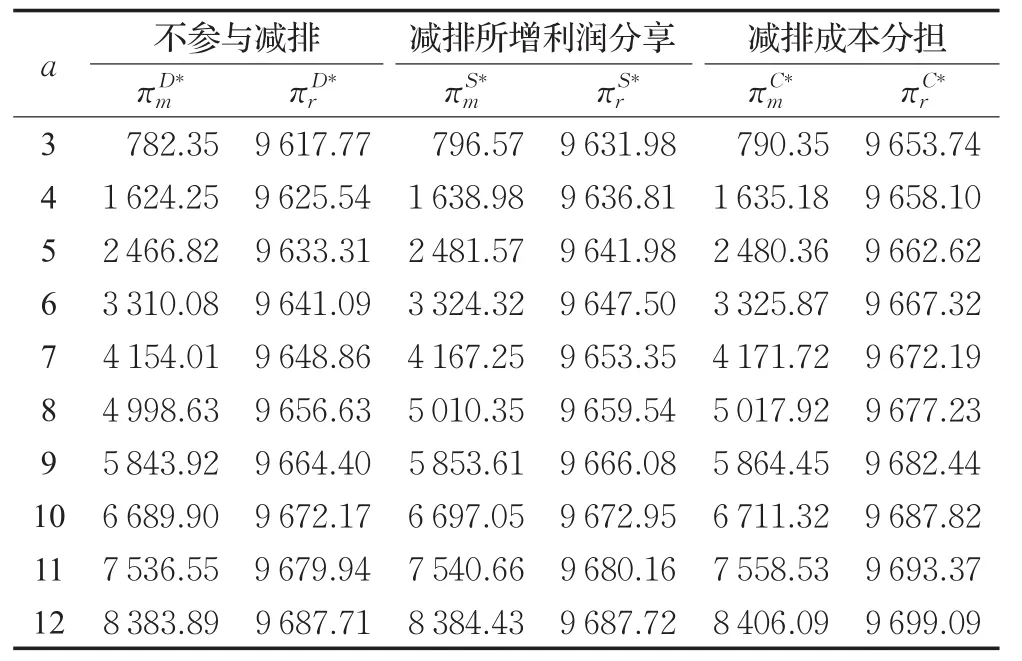
5.2 单位产品碳排放上限的变化对各模式下成员利润的影响
5.3 奖惩系数的变化对各模式下决策结果和成员利润的影响
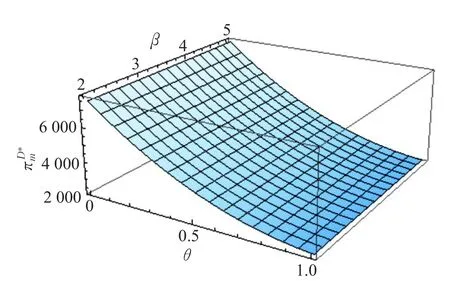
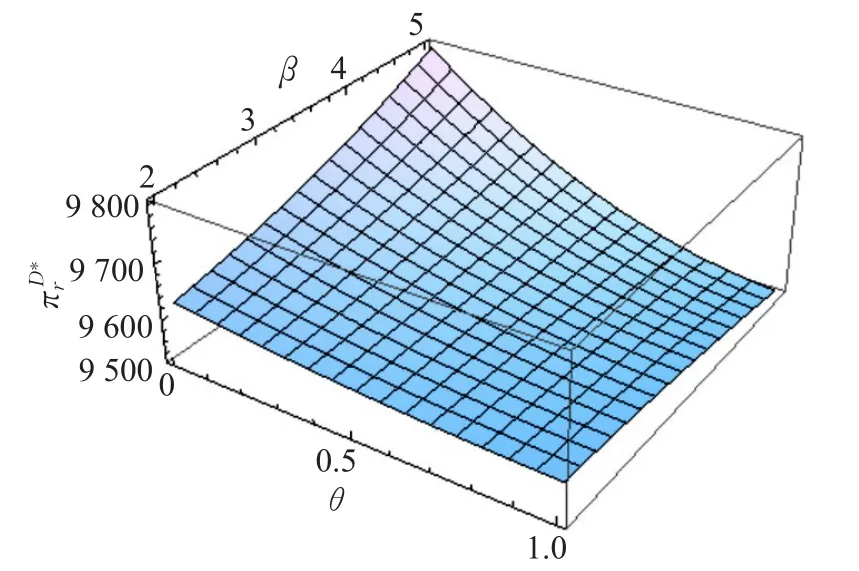
5.4 减排率对需求的影响因子和碳排放量的比值对各模式成员利润的影响

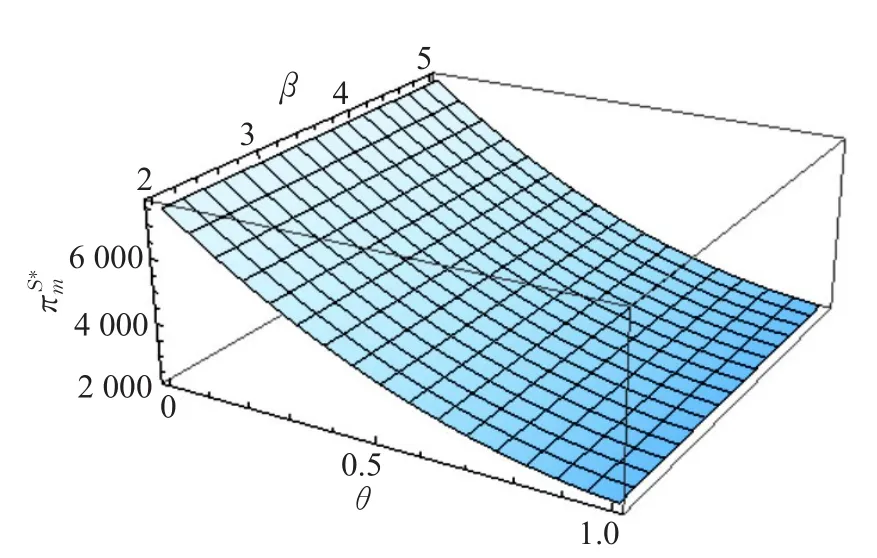

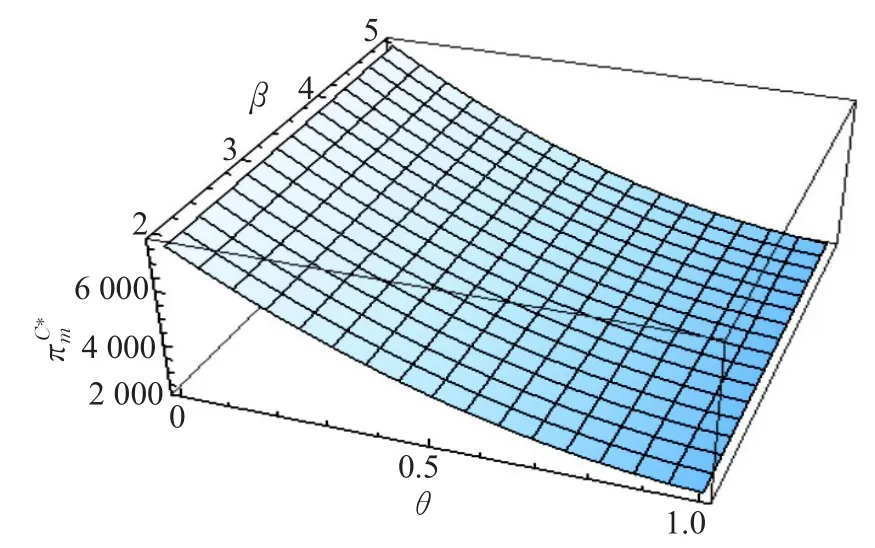

6 小结
