考虑评价信息满意度的群体信息集结方法研究
2019-07-10宫诚举易平涛郭亚军李伟伟
宫诚举, 易平涛, 郭亚军, 李伟伟
(1.哈尔滨工程大学 经济管理学院,黑龙江 哈尔滨 150001; 2.东北大学 工商管理学院,辽宁 沈阳 110169)
0 引言
群体评价是指多个评价者参与的综合评价问题,信息集结是群体评价问题不可忽视的重要环节,群体信息的集结质量直接影响最终的群体评价结果,因而群体信息集结方法的研究一直是综合评价领域的热点问题,目前已取得丰硕的成果,具体可以归结为以下几类:(1)基于OWA算子的信息集结方法[2~5]。文献[2]对模糊语言诱导的广义OWA算子进行了研究,并将其应用到模糊语言的决策问题中;文献[3]对OWA算子研究的最新情况进行了可视化的分析和总结,并得出OWA算子在多属性决策中的研究是目前的最新研究方向。(2)基于密度算子的信息集结方法[6~9]。文献[6]对诱导密度算子及其性质进行了详细的分析;文献[7]将密度算子扩展到评价信息为二元语言的情况中;文献[8]根据信息分布的疏密程度,提出二维密度加权算子并将其应用在群体信息的集结中。(3)针对AHP法中判断矩阵的集结方法[10~12]。文献[10]通过计算最优可能满意度的群判断矩阵对评价信息进行集结;文献[11]运用植物模拟生长算法探讨群体专家判断矩阵的集结方法;文献[12]分别对区间数AHP法和区间数模糊判断矩阵的集结方法展开了研究。(4)基于信息偏好的信息集结方法[13,14]。文献[13]提出基于群组判断集合离差的同质性信息集结方法并用于群体决策中;文献[14]提出两种使群体达成共识的方法并对基于个体偏好的群体信息集结方法进行研究。
从群体评价的角度看,由于参与评价的人数及需要集结的数据相对较多,因此信息集结变的更加复杂。对于集结群体信息的一类解决方法是,根据不同评价者的重要程度确定不同评价者的权重系数,然后按加权平均法进行信息集结,但这类方法存在2个问题:(1)忽视评价者的经验信息对信息集结结果的影响,而经验信息可以用于辅助判断评价者提供的信息的可能准确程度;(2)评价者权重通常代表评价者给出的所有评价信息的权重,而同一评价者对被评价对象不同评价指标的认知程度很可能不相同,因而应根据评价信息的不同赋予同一评价者不同的权重。针对上述2个问题,本文提出一种考虑评价信息满意度的信息集结方法,以进一步提高群体信息集结的科学性和准确性。
1 问题描述
设评价者集合为S={s1,s2,…,sn},被评价对象集合为O={o1,o2,…,op},评价指标集合为X={x1,x2,…,xm},评价者初始权重的集合为Ω={ω1,ω2,…,ωk},由评价者的经验信息确定。xijk表示评价者sk对于被评价对象oi关于评价指标xj的赋值,yik表示评价者sk给出的被评价对象oi的评价值,其中i=1,2,…,p;j=1,2,…,m;k=1,2,…,n,不失一般性,令m,n,p≥3,由xijk组成的评价信息矩阵如表1所示。如何将每个评价者的评价信息(xijk或yik)集结到一起是本文解决的重点问题。

表1 各评价者的指标信息
2 基于评价信息满意度的信息集结方法
评价信息满意度是指按照某一原则或从某一(些)方面对评价信息(本文主要指评价者的经验信息和评价过程中的信息)的满意程度的数值测量。具体方法如下。
2.1 评价信息满意度矩阵的确定
对各评价者的原始评价信息数据{xijk}或{yik}进行预处理,为方便起见,记预处理后的指标数据仍为{xijk}或{yik},并使xijk∈(0,1),yik∈(0,1)。
(1)指标信息满意度矩阵的确定

(1)
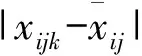
可用熵值法计算ξjk[1]。具体计算过程如下:

(2)
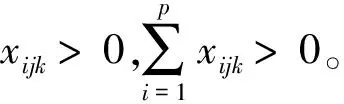
(3)
3)计算各评价者的不同评价指标包含的信息量ξjk
(4)
其中ξjk∈(0,1)。

(2)评价结果满意度矩阵的确定
评价结果满意度矩阵的确定方法与指标信息满意度矩阵的确定方法类似,不同的是评价信息满意度矩阵的个数与评价者的个数相同,而评价结果满意度矩阵只有一个。

(5)
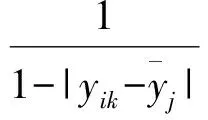
2.2 评价者权重的确定
由于根据先验信息(如权威度、知识水平、实践经验等)确定的评价者初始权重对当前实际问题的考虑相对较少,甚至会出现与实际情况不符的情况,因此应利用本次评价活动的评价信息对评价者初始权重进行修正。
由先验信息确定评价者初始权重的方法
本文由先验信息确定的评价者初始权重主要通过评价者的先验信息满意度进行衡量,评价者的先验信息满意度则通过各评价者在过去几次参与评价活动中给出的评价结果与该评价活动最终的评价结果的相似程度确定,具体方法如下。
(6)
式中,μk表示评价者sk的先验信息满意度,gk(ta)表示评价者sk在过去ta(a=1,2,…,h)时刻的先验信息满意度的大小(可以采取打分等形式确定),πa为ta时刻的先验信息满意度的权重。πa的值可按模型(7)计算,其含义见文献[15]。
(7)
其中“时间度ε”可根据实际情况按表2确定。

表2 “时间度”的标度参考表
因此评价者初始权重的计算如下:
(8)
评价者修正权重的确定
(1)集结指标信息时评价者权重的修正
当集结指标信息时评价者初始权重的修正原则是对不同指标信息分别修正,方法如下:
(9)
式中,rijk表示对评价者sk的指标信息xijk的权重修正系数,通过aijk影响评价者sk对评价指标xj的整体认知程度和对被评价对象oi的整体认知程度共同确定,ωijk表示对xijk的赋权,rijk的计算方法如下:
(10)
式中,fijk表示评价者sk对被评价对象oi的总体认知程度受指标信息xijk的影响程度,gijk表示评价者sk对评价指标xj的总体认知程度受指标信息xijk的影响程度,fijk和gijk的计算方法如下:
(11)
(12)
(13)
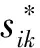
(14)
(15)
(16)
(2)集结评价值时评价者的修正权重
集结评价值时评价者初始权重的修正原则是对各评价者给出的不同评价值分别修正,具体方法如下:
(17)
式中,lik为权重修正系数,表示评价者sk对被评价对象oi的整体认知程度,zik表示修正后各评价者不同评价结果的权重,lik的计算方法如下:
(18)
2.3 基于评价信息满意度的群体信息集结模型
当集结指标信息xijk时,按照§2.2计算出的各评价者权重矩阵如下:
(19)
当集结信息为评价值yik时,根据§2.2计算出的各评价者的权重向量如下:
Zk=(z1k,z2k,…,zik)
(20)
因此当评价信息为指标信息时的集结方式为:
(21)
当评价信息为评价值时的集结方式为:

(22)
2.4 群体信息集结的具体步骤
综上所述,归纳出基于群体评价信息满意度的信息集结方法的步骤:
步骤1收集参评价者的相关信息,利用式(6)及式(7)确定对各评价者的先验信息满意度,并利用式(8)确定各评价者的初始权重ωk。
步骤2请各评价者根据实际问题分别给出评价信息,并对这些信息进行预处理。
步骤3利用熵值法和式(1)~式(5)计算需要集结的评价信息的满意度矩阵Ak或E。
步骤4根据式(10)、式(16)或式(18)计算各评价者的权重修正系数rijk或lik,并根据式(9)或式(17)计算各评价者的修正权重矩阵Ωk或向量Zk。
步骤5根据不同的评价信息,选择式(21)或式(22)对评价信息进行集结,计算出群体信息最终的集结结果X或Y。
2.5 关于方法的几点说明
(1)评价信息满意度的确定综合考虑了单个评价者局部信息的离散程度和所有评价者同一信息间的偏离程度。
(2)对先验信息确定的评价者初始权重进行修正,有利于降低因先验信息不能完全反应各评价者在此次评价中的表现而出现的专家权重不合理的问题。
(3)评价者的初始权重在修正的过程中分解成多了个权重,避免以一个评价者权重代表该评价者所有评价信息重要程度的弊端。
(4)信息集结过程中选择“和型”公式,可以突出满意度高的评价者的作用,但根据实际问题也可以选择不同类型的集结模型。
(5)由于方法中采用了熵值法,因此要求预处理后的指标值大于零,所以在指标数据的预处理过程中需要注意该问题。
(6)若出现各评价者对同一被评价对象的同一指标的预处理值完全相同的极端情况,该方法失效。
3 应用算例
某市预实施一项电动汽车充换电设施工程项目,目前有4个方案并请4位专家对其从6个指标进行评价,这6个指标分别是安全可靠性x1、先进性x2、经济效益x3、造价控制x4、环境影响x5和实用性x6,所有指标信息均由评价者结合实际情况给出(已做预处理)见表3~表6,各评价者过去5次参与评价活动时的信息(先验信息的打分)见表7。
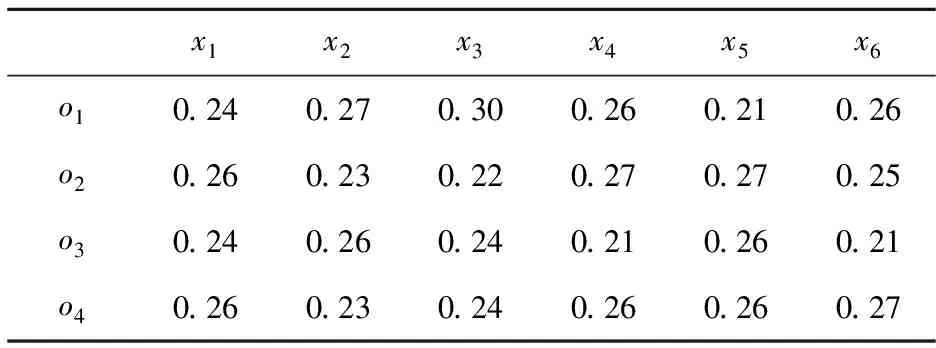
表3 专家s1给出的指标信息

表4 专家s2给出的指标信息

表5 专家s3给出的指标信息

表6 专家s4给出的指标信息
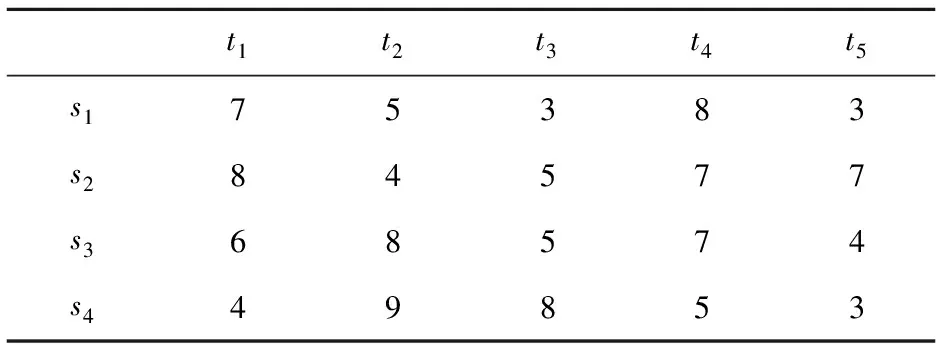
表7 各专家过去评价活动的评分
应用本文的研究做如下计算:
(1)按式(7)可得πa=(0.128,0.157,0.192,0.235,0.288),按式(6)可得4位专家的先验信息满意度分别为5.001,6.273,5.781,5.500,根据式(8)可得4位专家的初始权重为ωk=(0.22,0.28,0.26,0.24)。
(2)按式(1)~式(4)计算4位专家的评价信息满意度矩阵,其中c=0.5,为节省篇幅,表8仅列出专家s1的计算结果(下同)。
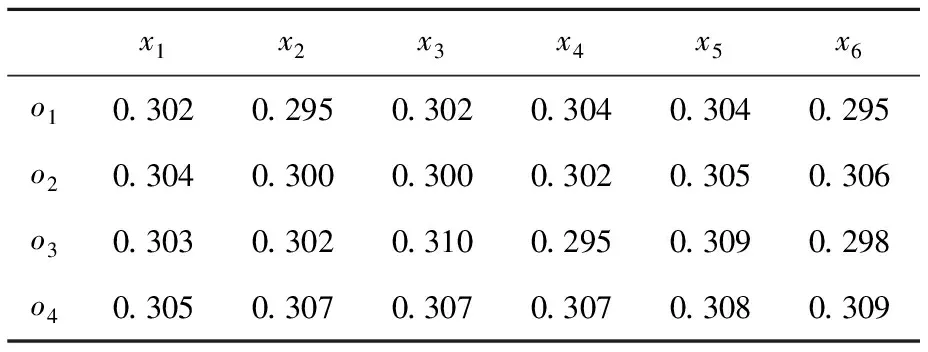
表8 专家s1各指标信息的满意度
(3)根据式(10)~式(16)计算4位专家权重的修正系数,结果见表9。

表9 专家s1的权重修正系数
(4)根据式(9)计算4位专家的权重矩阵,计算结果见表10。

表10 专家s1的权重矩阵
(5)按式(21)求解最终集结成的群信息,结果见11。

表11 最终的群集结结果
从各评价者的权重矩阵中可以看出,在信息集结的过程中各评价者的指标信息中的不同元素的重要程度是不同的,同一评价者不同元素的权重差距甚至很大,说明本文提出的方法能够反映出同一评价者给出的不同评价信息的准确程度是不同的,因此应根据信息的变化赋予其不同的权重,这也与实际情况相符。
4 结束语
针对如何集结多个评价者的评价信息问题,本文通过考虑评价信息的满意度,对群体信息的集结方法进行了研究,其特色主要有:(1)提出评价信息满意度的概念,尝试性的从离散程度的角度对其进行测度,并从群体评价信息满意度的角度构建信息集结方法,(2)考虑了评价者先验信息的重要作用,并综合利用评价者的先验信息以及评价过程中的信息确定各评价者的权重。(3)方法打破以往研究中评价者权重固定不变的思想或做法,而是在集结过程中对评价者的不同信息赋予不同的权重,使处理过程更加公正、合理。文中最后通过一个算例说明了方法的应用过程,从算例也可以看出本文提出的群体信息集结方法的合理性。
