基于聚类的流面自动布局及生成算法

唐 烨，解利军，桂立业，何丽莎，郑 耀

浙江大学 航空航天学院，杭州 310027

1 引言

流场可视化是科学可视化的经典分支之一。通过直观的图像来表示抽象的流场数据[1]，既可以加快从数据中获取信息的速度，又能让不具备领域专业知识的人理解这些信息。如今在航空航天、气象、自动化等领域的科学研究过程中，流场可视化已经成为不可或缺的技术。

流面可视化是流场可视化的一种方式，近几年来越来越流行[2]，相比于常用的流线法，流面法更适合表现复杂的流场结构[3]，并且展现更丰富的流场局部信息[4]。

1.1 相关概念

流场是一种矢量场。在空间坐标系(x,y,z)中，任意点(x0,y0,z0)都有唯一确定的向量(Vx,Vy,Vz)与之对应，就说在空间(x,y,z)范围内存在矢量场V。在流场中，该矢量场即速度场。

流线是一个无质量的质点（种子点）在某一稳定流场中以某点为起点，在该流场中运行的轨迹。流线上的每一点都与流场中该点对应的速度相切。假设V(x)是一个三维向量场，在时刻t经过点x0的流线为L(x0,t)，其中L(x0,t)满足公式（1）：

类似于流线的概念，流面是某条种子线C的所有种子点以C中的位置为起点在稳定流场中运行的轨迹的集合，设该流面为S，S满足公式（2），流面S中的点处处与流场中该点处的速度相切[5]。

其中S(s,t)是种子点C中s处的种子点在流场中的运动轨迹，也就是由C中s处的种子点生成的流线，S为C中所有点生成的流线的集合，如图1所示。

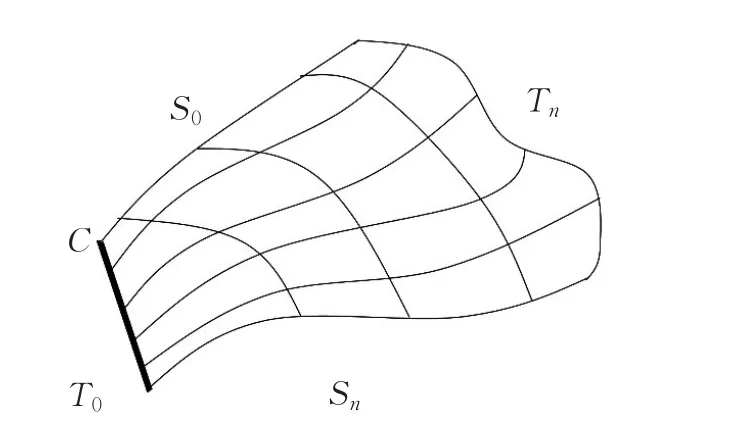
图1 流面示意图

1.2 相关工作

Hultquist首先在1992年提出了一种高效的流面生成算法——前沿推进算法。其基本思想为相邻的两条流线之间形成流带，每条流带需要记录两个前沿位置点，算法通过推进每条流带的前沿位置的方式来构造流面，其特别之处为前沿的个数并不是固定的，当某条流带前沿距离过大时可以通过加入新点分裂流带来提升流面精确度，当前沿过窄时可以考虑合并相邻流带来减少计算与存储资源的消耗[5]。

前沿推进法非常适用于流场中存在大量的流线分散与流线聚拢的情况，即流场中速度大小基本稳定，但方向出现偏差的情况，并且也较易于实现。但当流场中的速度大小分布不匀称时，前沿推进法就难以适用。为此Garth在2004年提出了一个基于Hultquist算法的新算法，其基本思想为，在前沿推进时前进的距离以弧长为参数而不是固定的时间参数，同时在分裂与合并流带时考虑曲率，使得最后得出的图像能够更精确[6]。

Scheuermann提出了一种在四面体网格中生成流面的算法[7]，其基本思想为通过重心坐标在每个四面体内计算出规则表面，通过面上的线段组成最终流面。这种方法能够有效地利用流场中的拓扑结构信息，但用这种方法最终生成的流面质量十分依赖于网格的密度[7]。

与以上这些显示计算曲面的算法不同的是，Wijk在1993年提出过一种通过定义网格边缘的标量函数的方式来隐式地计算曲面的算法[8]，但由于它无法将所有可能的曲面都计算出来，因此应用范围并不广。

Schneider等人在2009年提出在构造曲面的时候用施密特插值法取代线性插值法[9]，其计算所需的额外数据都可以在流线生成过程中通过计算得出，可以将曲面的精确度提升到4阶。

Schulze等人提出过一种强制流面前沿线与流场中的速度垂直的方法，它可以在湍流区生成高质量的流面[10]。

以上都是确定种子线情况下所用的流面生成算法，但是当拿到流场数据时，无法确定在哪里布线能够得到较好的结果。因此本文介绍一种种子线自动布局以及流面生成的算法。

本文的主要思想：流场中不同区域的流动情况并不一致。如图2所示，以流线法表示，可能有直线区域、曲线区域、涡流区域。可以通过聚类算法将这些区域进行划分。划分后的每个聚类可以用一个流面表示。生成流面的方法为，首先从分区中心点出发，沿着流场的曲率场在该分区范围内积分得到种子线。选择在曲率场中积分是因为：（1）曲率场中任意点的方向与流场中该点处的速度方向垂直，而垂直于流场速度方向的种子线生成的流面能够覆盖较大的范围。（2）沿着曲率场生成的种子线所生成的流面更能表现出流场的流动结构。得到种子线后，通过前沿推进法配合施密特插值法生成光滑流面。

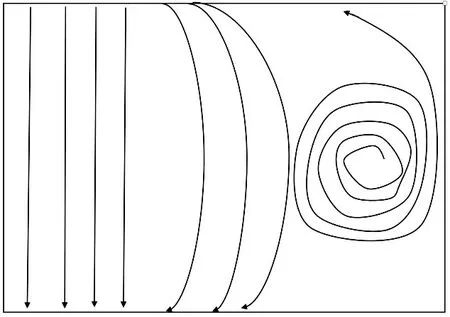
图2 流场不同区域示意图

2 流场的分区和种子线布局

2.1 程序流程

该算法处理的对象是流场数据V(X)∈R3，其中V∈R3，X∈R3，X代表流场空间中点的坐标，V(X)代表点X处的速度。

图3为程序的流程图，对于流场中每个点P，首先算出它的曲率|C|以及速度模的梯度G用于之后的聚类以及种子线生成，详见2.2节。随后可以用改进版的K-means算法将流场中的点集划分为K个类，详见2.3节，其中K的值由用户自己输入。然后对于每一个类的聚类中心点，用四阶龙格库塔法在曲率场中进行积分得到K条种子线，详见第3章。对每条种子线，通过带施密特插值的前沿推进法生成并绘制流面，详见第4章。如果需要，用户可迭代该过程，修改参数再次进行聚类与流面生成工作。

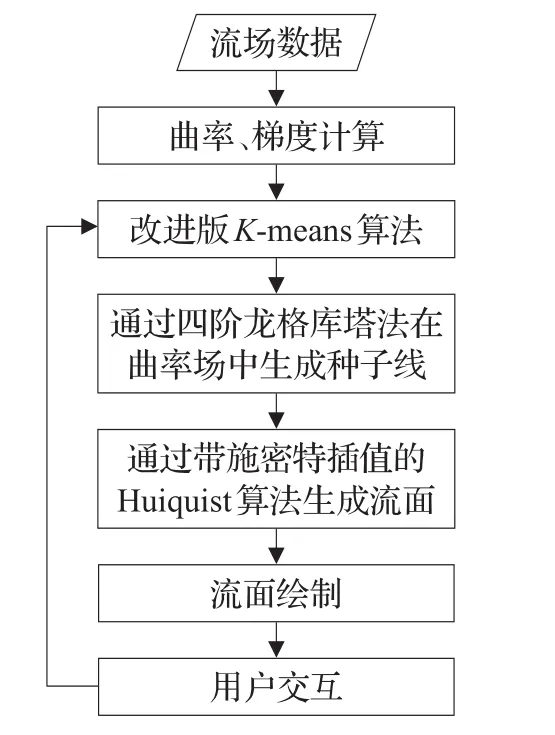
图3 程序流程图

2.2 流场中数据点间相似度计算

在三维空间点集中，两点间的相似度一般用它们的欧式距离来表示，但在流场数据集中，每个点除了坐标信息外，还有对应的速度信息。速度有两个基本属性：大小和方向。但由于关注的是潜在的种子线位置，因此希望把种子线布置在能够代表周围流线（速度）发生变化的区域。因此，并不是直接对流场中不同点间的速度进行比较，而要比较速度的变化情况。

同时，涡流位置也可以通过曲率值的大小来反映，而流场的结构也与涡流的位置有关[11]。

在流场空间中某处布置种子点形成流线S，则通过计算可以得到S中任意点P处的曲率|C|[12]，曲率也可以量化流线的弯折程度，也就是速度方向的变化程度。其中

其中V为点P处的速度，

点P处速度大小的变化情况|G|可以用速度模的梯度来表示，其中

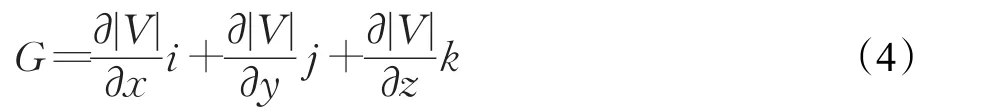
某点处速度的变化情况可以通过|C|与|G|的值来反映，则流场中点P1、P2间的距离Dis(P1,P2)可以定义为Dis(P1,P2)=|C1-C2|+|G1-G2|。

当P1、P2两点坐标间的欧式距离较大，而它们速度的变化量又相同的时候，Dis(P1,P2)为0，在聚类时会被归为一类，如果这两点的速度变化量较大，则它们应该代表两个潜在的布线区域。因此判定相似度时需要考虑两点间的欧式距离：Dis(P1,P2)=|C1-C2|+|G1-G2|+|X1-X2|。

流场数据中空间坐标与速度值的取值范围并不相同，因此相比于点坐标间的距离值，曲率值或梯度值间的距离值可能会显得很小。此时两点间的相似度无异于两点坐标间的欧氏距离，因此需要将它们全部归一化处理。

在对不同的流场数据进行聚类时，三个参数所占的权重未必一样，因此需要对三个参数进行加权，最终两点间相似度Dis(P1,P2)表示为：

其中，α为两点间相似度中二者的欧式距离所占的份额，β为速度变化量的两个参数中曲率所占的份额，0<α<1，0<β<1。

2.3 基于改进的K-means算法进行流场聚类

聚类是将对象的集合按照一定的标准分割成多个相似子对象集合的过程，同一类中的对象间相似度较高，不同类间对象间相似度较低。

聚类算法可以分为两大类：基于层次与基于划分。在此基础上还有三小类[13]：基于密度、基于模型、基于网格。

K-means算法属于基于划分的聚类法，与其他方法相比，有着实现简洁与运行快速两大优点。因此本文选择该方法进行流场聚类。

传统K-means算法中初始聚类中心的选取完全是随机的，而经过实验发现K-means算法的效果会受到初始聚类中心的影响。选取不当的初始聚类中心会使聚类过程更加漫长[14]。

因此，针对K-means算法在初始聚类中心选取上的盲区进行一定的改进。如果K个初始聚类中心互相之间具有较高的相似度，那么它们最后很有可能属于同一个聚类，这会影响后续聚类的时间，于是希望K个初始聚类中心间的相似度尽可能得低。其过程如下：

（1）在数据集中随机选择一个初始种子点。

（2）对于数据集中所有点P，记录其与聚类中心集合中的点Ci的距离的最小值D(P)。

（3）选择一个新点加入到聚类中心集合中，选取的原则为D(P)值越大，被选中的概率也越大。

（4）如果得到K个聚类中心，执行下一步，否则，返回到第（2）步。

（5）对于数据集中所有点，将其划分到与它相似度最高（距离最小）的聚类中心所属的聚类中。

（6）对于每一个聚类，选择到类中所有点的距离和最低的点作为新的聚类中心。

（7）如果本次迭代得到的K个聚类中心与上次迭代得到的K个聚类中心相同，则聚类情况已经稳定，结束程序，否则，返回到第（6）步。

实验表明，采用改进版的K-means算法能够在参数一致的前提下，减少聚类过程中的迭代次数，减少聚类所需时间，如表1所示。

表1 两种K-means算法比较

聚类效果如图4所示，其中图4（a）为 α=0.5、β=0.3、k=2时的聚类效果。图4（b）为 α=0.8、β =0.8、k=4时的聚类效果，图4（c）为 α=0.5、β =0.8、k=6时的聚类效果。

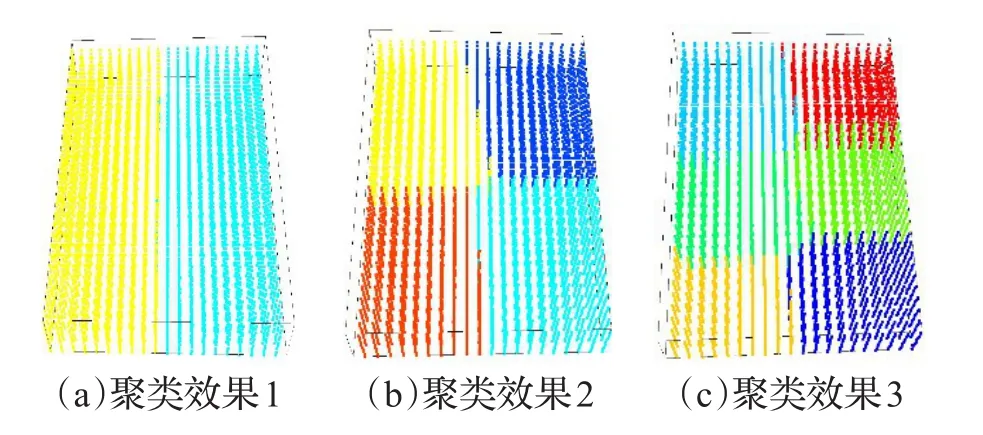
图4 聚类效果图

3 种子线生成

得到了流场的聚类与中心数据后，就可以着手种子线的生成工作，流场的聚类中心虽然能代表流场的聚类，但单凭一个点难以确定种子线，还需确定种子线生成的方向与长度。

通过观察可以得知，与速度方向平行的种子线无法生成流面，与速度方向垂直的种子线生成的流面能覆盖较大范围[15]，如图5所示，图中蓝色带箭头曲线代表流线方向，x为垂直流场方向种子线，红色曲线为不与流场垂直的种子线。二者生成同一流面，但种子线X更短。

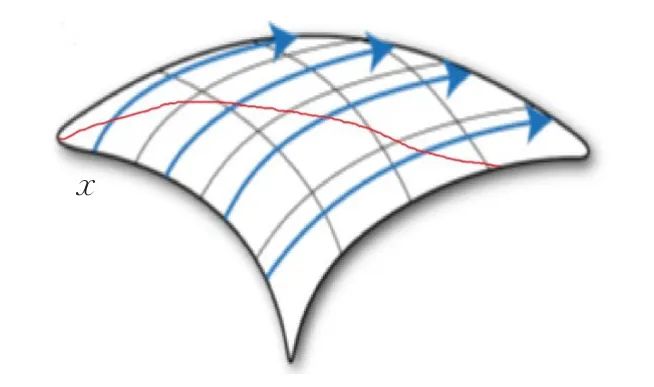
图5 种子线示意图

种子线的朝向需要考虑到流场局部位置的结构信息，否则，生成流面效果将大打折扣。如果流面处处与曲率方向相切并且平行于旋转轴，那么它可以表现出螺旋流的特性。如果该面垂直于曲率方向和旋转轴，该流面就难以传达出足够的有效信息。如图6所示，图6（a）为以垂直于速度与曲率方向生成的种子线所形成的流面，图6（b）为垂直于速度方向平行于曲率向量方向积分形成的种子线生成的流面，可以看到图6（b）中的内容包含了图6（a）的主要内容。

图6 种子线垂直曲率与平行曲率效果图

根据流线中的曲率定义，曲率向量C由流线的速度向量V与加速度向量a通过叉积得出，因此C向量的方向一定是与V垂直，即给定一个初始点P，在常流场生成曲率场中的运动轨迹必定处处与流场中该点处的速度垂直。因此，最终种子线生成方法是：以聚类中心点P为初始点，在曲率场中以生成流线的方法通过积分生成种子线。

由于每个聚类中心只能代表各自所属的聚类。因此，种子线沿着曲率场积分到达分区边界时，停止积分。

积分使用龙格库塔法（Runge_Kutta）来实现。

四阶龙格库塔法为：

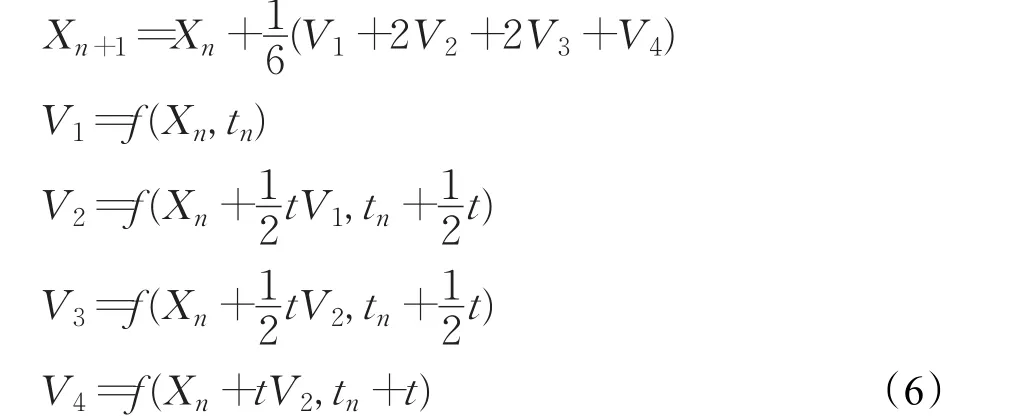
种子线效果如图7所示，其中图7（a）为α=0.5、β=0.3、k=2时生成的种子线，图7（b）为 α =0.8、β =0.8、k=4时生成的种子线，图7（c）为 α=0.5、β =0.8、k=6时生成的种子线。

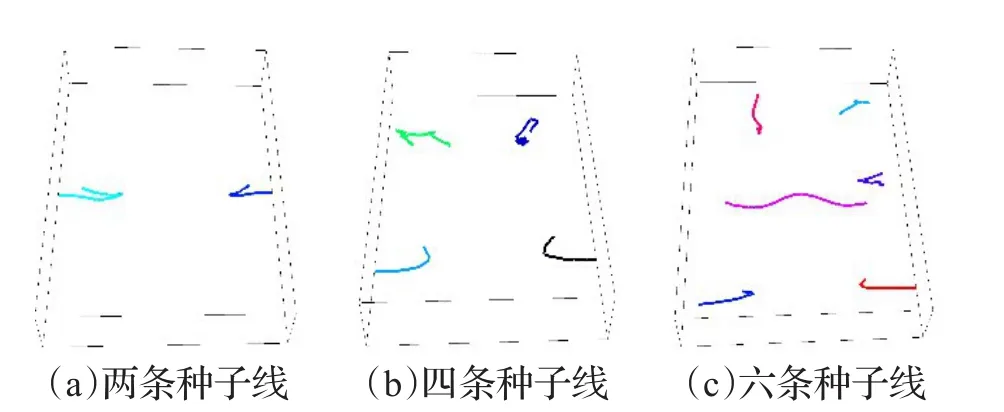
图7 种子线效果示意图

4 流面生成

得到种子线后就可以开展流面的生成工作，基本的思想采用前沿推进法，如图8（a）所示。前沿推进法将流面划分为若干流带，相邻两条流线之间构成一条流带，记每条流线当前最新采样点为前沿，每个流带对应一个追踪器记录其两个前沿。追踪器通过单链表的方式连接，如图8（b）所示，流带通过前沿在流场中推进的过程来生成。当流场中前沿处速度为0，或者前沿位置超出流场空间时，该流带结束生成。

图8 三角化法基本思想示意图

流带通过三角形面片法表示，即在相邻的两条流线的采样点上生成三角形条带来近似化表现流带，三角形的形状需要尽量规则，角度不宜过大，这可以通过局部贪心法，即每次新增对角线较短的三角形，来实现。两条流线的前沿在流场中各生成一个新的采样点后，与追踪器中记录的前沿点一起就可以构成一个四边形，选择较短对角线与两前沿连线构成三角形面片加入流带中，并更新追踪器中的前沿信息。其过程可用如下伪代码表示。

输入：以单链表形式相互连接的追踪器Tracer，流场数据V，三角形面片集合Output

输出：无

Advance_Font（Tracer）

1.Left_advanced=false；

2.while（1）

3.L0=Tracer->L0，R0=Tracer->R0；

4.在V中通过龙格库塔法以L0、R0计算L1、R1

5.L_diag=|L1R0|，R_diag=|L0R1|

6.M_diag=min（L_diag，R_diag）；

7.if（M_diag==L_diag）

8. ad_left=true；

9.else ad_left=false；

10.if（Left_advanced&&ad_left）return；

11.if（ad_left）

12.Output->push_triangle（L0，R0，L1）；

13.Tracer->L0=L0=L1；

14.Left_advanced=true；

15.else

16.Output->push_triangle（L0，R0，R1）；

17.Advance_Font（Tracer->next）；

18.Tracer->R0=R0=R1；

随着流场中流线的分散与聚拢，流带的宽度也会产生变化，当流线不断聚拢时，流带的宽度会变窄，置之不理的话会生成多余的三角形，影响到绘制的时间，此时可以考虑将其与相邻流带合并。当流线不断分散时，流带的宽度会增大，置之不理的话，会影响到生成曲面的精确度，此时可以考虑将该流带分裂。

判断合并的标准：如图9（a）所示，流带Ribbon1当前的两前沿分别为L0、M0。其相邻流带Ribbon2的两前沿为M0、R0。通过L0、M0、R0三点积分得到的采样点为L1、M1、R1。定义四边形L0L1R1R0的高H为L1与R1两点到线段L0R0所属直线的距离的较小值。当点L1与点 R1间的距离小于 H，且 L0、L1、M0、M1、R0、R1六点近似共面时，将流带Ribbon1与流带Ribbon2合并。

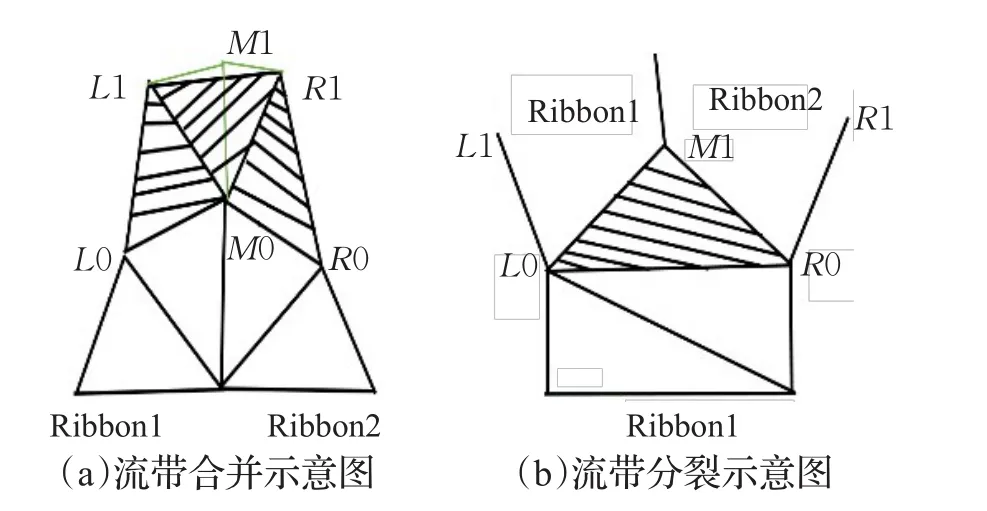
图9 流带合并分裂示意图

合并流带的方法：如图9（a）所示，在流带Ribbon2中，选择对角线M0R1，将∆M0R0R1加入到流带中，更新右前沿为 R1，在流带Ribbon1中，选择对角线L1M0，将∆L0M0L1加入到流带中，更新追踪器1左前沿为L1，将∆L1M0R1加入到流带中，将追踪器1右前沿更新为R1，并将追踪器1右边的追踪器更新为追踪器2右边的追踪器。其过程如下伪代码所示：

输入：非队尾追踪器Tracer，流场数据V，三角形面片集合Output

输出：无

Merge_Ribbon（Tracer）

1.L0=Tracer->L0，M0=Tracer->R0；

2.R0=Tracer->next->R0；

3.在V中通过龙格库塔法以L0、M0、R0计算L1，M1，R1

4.Output->push_triangle（L0，L1，M0）；

5.Output->push_triangle（M0，R0，R1）；

6.Output->push_triangle（L1，M0，R1）；

7.Tracer->L0=L1，Tracer->R0=R0；

8.Tmp=Tracer->next

9.Tracer->next=Tracer->next->next；

10.Delete tmp；

判断分裂的标准：当新采样点L1与点R1的距离|L1R1|大于四边形 L0L1R1R0的高 H的两倍，即|L1R1|≥2H时，流带需要分裂。

分裂流带的方法：如图9（b）所示，在流带中用适当的方法加入新点M1，将∆L0M1R0加入流带中，生成新流带Ribbon2，其左前沿为M1，右前沿为Ribbon1的右前沿R0，更新Ribbon1的右前沿为M1。将Ribbon2右边的流带设置为Ribbon1右边的流带，Ribbon1右边的流带设置为Ribbon2。其过程如下伪代码所示：

输入：追踪器Tracer，流场数据V，三角形面片集合Output

输出：无

Split_Ribbon（Tracer）

1.L0=Tracer->L0，R0=Tracer->R0

2.通过龙格库塔法在V中以L0、R0计算L1、R1

3.计算新加入点M1的坐标

4.Output->push_triangle（L0，M1，R0）；

5.Tracer->R0=M1；

6.New Tracer2；

7.Tracer2->L0=M1，Tracer2->R0=R0；

8.Tracer2->next=Tracer->next；

9.Tracer->next=Tracer2；

加入新点M1的坐标在取线段L1R1中点的基础上配合施密特插值法使得最后生成的流面更平滑。其基本思想如图10所示。

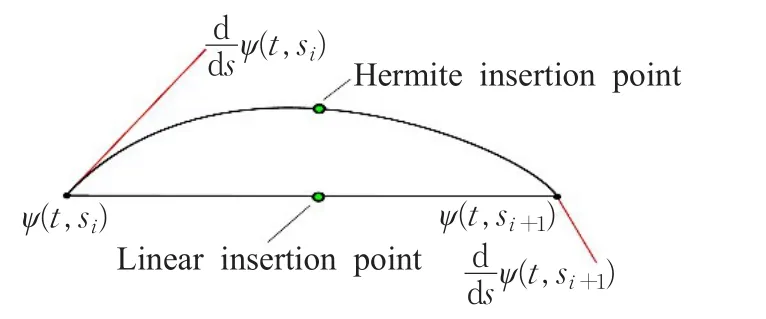
图10 施密特插值法示意图

在插入新点时考虑到流场沿着种子线方向的变化，决定点M1是位于中点偏上还是偏下，其计算方法为：

其中，，由于是基于中值法改进，通常r取0.5。

流面生成效果如图11所示，直接三角化法得出的图像由于无法适应流线变化会产生失真，如图11（a）所示。前沿推进法产生的图像不够平滑，如图11（b）所示。配合施密特插值法则能得到平滑又精确的流面，如图11（c）所示。

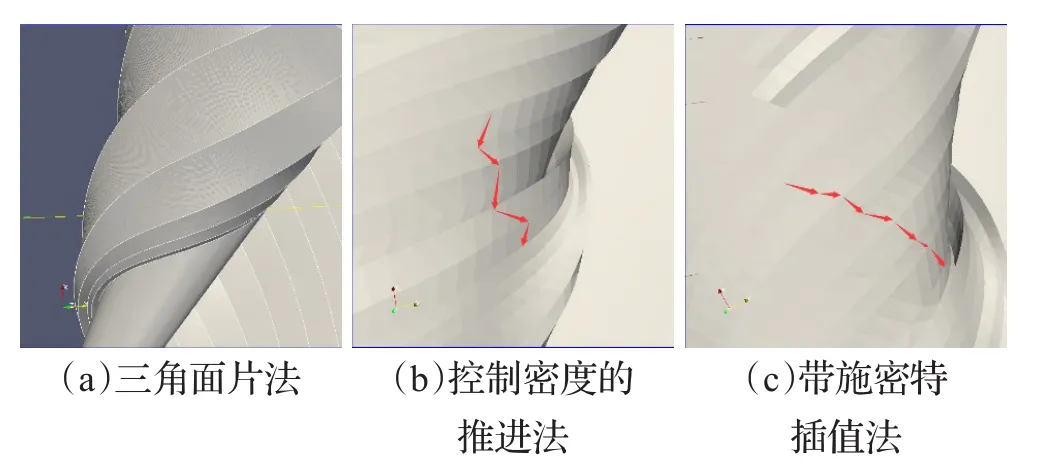
图11 流面效果图

5 实验结果分析

测试平台为Win 10操作系统，Intel CORE i7，8 GB内存，显卡为NVIDIA GEFORCE GTX 860M。

图12展现了通过自定义种子线与通过本文算法自动布线在Delta-wing流场数据中生成流面的情况：图12（a）为连接端点（0.334 5，－200，40.404）与（0.334 5，200，40.404）为种子线生成的流面，图12（b）为连接端点（201.003，－200，90.909）与（201.003，200，90.909）为种子线生成的流面。可以看到它们都属于比较稳定的流面，且值覆盖了流场中一小部分，难以对流场整体结构进行描绘。图12（c）是用本文方法以 K=2，α=0.5，β=0.3生成的流面，可以看到它画出了两块近似对称的区域。图12（d）是用本文方法以 K=4，α=0.5，β =0.8生成的流面，可以看到在两块对称区域的基础上增加了两块平滑曲面，图12（e）是用本文方法以 K=6，α=0.8，β=0.8生成的流面，可以看到相对于图12（d）中图像，新增了两块平滑曲面，它们找出了流场中变化较剧烈的部分，并生成了有代表性的图像，并且由于图12（e）中的图像相比图12（d）中的图像并无剧烈的变化，不再追加聚类个数。另外，用Esturo的方法在Telda-wing上所得图像[15]，只能生成一张流面，容易给人造成流场中只有该区域有流动的错觉，从而对流场整体的状况产生误判。

图13展示了通过自定义种子线与本文方法在5Jet流场数据中所生成流面的情况。图13（a）为连接端点（1，64，90）与端点（128，64，90）为种子线所生成的流面，图13（b）为连接端点（1，64，64）与端点（128，64，64）为种子线所生成的流面。可以看出，这两张流面都只能反映出流场局部的流动情况，无法对该流场整体的流动情况作出判断。图13（c）是本文方法以 K=2，α=0.3，β=0.3生成的流面。图13（d）是本文方法以K=4，α=0.5，β=0.8生成的流面，保持整体结构的同时增加了平滑曲面。图13（e）是以 K=6，α=0.5，β =0.3生成的流面，保持图13（d）中整体结构的同时新增了两张平滑曲面。至此，认为5JET数据的整体流动结构已得出，不再增加聚类个数。

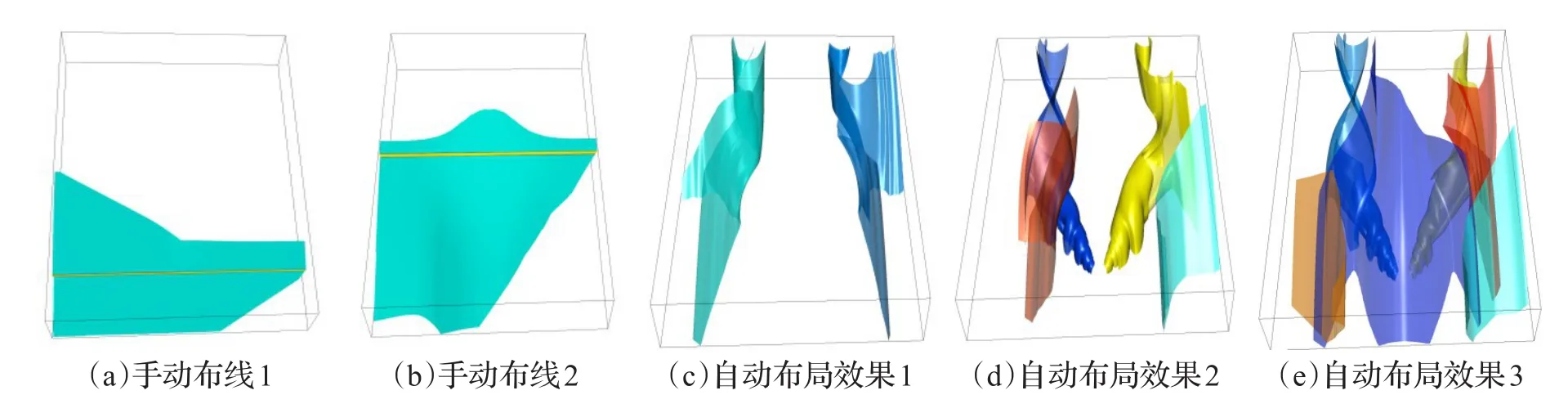
图12 Delta-Wing实验结果图

图13 5JET实验结果图

6 结论

本文设计了一个流场种子线自动布局以及流面自动生成的算法，通过坐标、曲率以及梯度参数对数据点进行聚类，得到中心点，在曲率场中通过四阶龙格库塔法得到种子线，然后基于前沿推进法得到流面，能够有效地在未知流场数据中生成表现力较强的流面，也能为人工布线位置提供较好的参考。目前，该算法还需要用户自己输入聚类个数K，希望将来能够开发出自动确定聚类个数的算法。该算法依然是串行执行的版本，未来将实现并行计算的版本，以提高程序运行的速度。此外，该算法所生成的流面依然存在流面间遮挡的问题，将来希望开发出能够根据观察者视角与流面遮挡情况自动调节局部透明度的版本。

[1]宋汉戈，刘世光.三维流场可视化综述[J].系统仿真学报，2016（9）：1929-1936.

[2]Edmunds M，Laramee R S，Chen G，et al.Surface-based flow visualization[J].Computers&Graphics，2012，36（8）：974-990.

[3]Mcloughlin T，Laramee R S，Peikert R，et al.Over two decades of integration-based，geometric flow visualization[J].Computer Graphics Forum，2010，29（6）：1807-1829.

[4]Laramee R S，Garth C，Doleisch H，et al.Visual analysis and exploration of fluid flow in a cooling jacket[C]//Proceedings IEEE Visualization 2005，2005：623-630.

[5]Hultquist J P M.Constructing stream surfaces in steady 3D vector fields[C]//IEEE Conference on Visualization（Visualization’92），1992：171-178.

[6]Garth C，Tricoche X，Salzbrunn T，et al.Surface techniques for vortex visualization[C]//Symposium on Visualization，Konstanz（Vissym 2004），Germany，May 2004：155-164.

[7]Scheuermann G，Bobach T，Hagen H，et al.A tetrahedrabased stream surface algorithm[C]//IEEE Visualization 2001，San Diego，CA，USA，2001：151-553.

[8]Wijk J J V.Implicit stream surfaces[C]//IEEE Conference on Visualization（Visualization’93），1993：245-252.

[9]Schneider D，Wiebel A，Scheuermann G.Smooth stream surfaces of fourth order precision[J].Computer Graphics Forum，2009，28（3）：871-878.

[10]Schulze M，Germer T，Rössl C，et al.Stream surface parametrization by flow-orthogonal front lines[C]//Computer Graphics Forum，2012：1725-1734.

[11]Banks D C，Singer B.Vortex tubes in turbulent flows：Identification，representation，reconstruction[C]//IEEE Conference on Visualization（Visualization’94），1994：132-139.

[12]Roth M.Automatic extraction of vortex core lines and other line type features for scientific visualization[microform][D].Swiss Federal Institute of Technology Zurich，2000.

[13]Rokach L.A survey of clustering algorithms[M]//Data Mining and Knowledge Discovery Handbook.Boston，MA：Springer，2009：269-298.

[14]Arthur D，Vassilvitskii S.k-means++：The advantages of careful seeding[C]//Eighteenth ACM-SIAM Symposium on Discrete Algorithms（SODA 2007），New Orleans，Louisiana，USA，January 2007：1027-1035.

[15]Esturo J M，Schulze M，Rössl C，et al.Global selection of stream surfaces[J].Computer Graphics Forum，2013，32（2pt1）：113-122.