基于秘密共享的组密钥协商方案
2018-06-26刘丰年苗付友
方 亮,刘丰年,苗付友
1.中国科学技术大学 计算机科学与技术学院,合肥 230027
2.三门峡职业技术学院,河南 三门峡 472000
1 引言
密钥协商是确保网络信息机密性的基础,也是无线传感器网络(WSNs)信息安全研究的热点之一[1-2]。然而,无线传感器节点具有计算能力弱、存储容量小、能量有限[1]等基本特征。进一步的,由于节点能量有限,节点自身的电能耗尽或损坏会导致节点的退出,从而需要不断补充新的节点,因此WSNs具有节点动态加入和退出的特点;由于在线第三方对计算能力和存储能力的要求,以及WSNs节点通信能力的限制,往往不适合在WSNs中部署可信在线第三方。因此,如何在节点计算、存储和能量有限,节点动态加入以及缺乏在线可信第三方的WSNs环境下,建立适合的密钥协商方案具有很大的挑战性。
Eschenauer and Gligor在2002年[3]较早提出WSNs中的密钥分发方案:每个节点携带拥有P个密钥的密钥池,需要通信的两个节点各自随机选择k个密钥,如果两个k-密钥子集包含相同的密钥,即实现了密钥的协议。不过,该方案很难应对节点被攻陷的情况。为了解决这一问题,Chan[4]提出“q-composite random key”的方案,在这个方案中,两个相邻节点至少需要Q个密钥才能建立安全信道。随后有很多方案提出在每对节点之间使用单个甚至更少的密钥建立安全信道的方法[5-7]。在一个网络中,如果每对节点之间都拥有一个私有的密钥,则n个节点一共需要n(n+1)/2个密钥。每个节点需要存储n个密钥,在大规模WSNs中,对节点的存储容量提出了非常高的要求。为此,Ruj[7]将每个节点所需的存储容量减少为O(n)级别,即使如此,在拥有大量节点的WSN中,仍然存在所需密钥存储容量过大问题。而使用组密钥的方案,使系统中需要通信的节点形成一个通信组,并共享相同的组密钥可以有效解决上述节点密钥存储容量问题。此外,一个发送节点使用组密钥进行多播、组播时仅需加密一次数据,即可实现对所有接收节点的数据发送。不仅如此,在多跳通信时,中间节点转发数据时无需再次加解密,能够减少通信的计算开销。故使用组密钥通信有利于降低数据通信过程中的计算开销。
Shamir[8]在1979年首先提出了(t,n)门限秘密共享概念,即将一个秘密分成n个share,只有t或多于t个share才能恢复秘密,而少于t个share则无法获得秘密的任何信息。门限秘密共享可以用来实现组密钥的协商。Wu等人[9]基于秘密共享提出了ad-hoc网络下的组密钥协商方案,其优点是拥有share更新机制。Harn等人[10]提出基于秘密共享的可认证组密钥方案,使用在线可信第三方广播信息进行组密钥的验证。这些基于秘密共享的组密钥协商方案优势在于每个节点只需很少的存储容量,而且即使一定数量的节点被攻破,系统仍然是安全的。随着WSNs中分层及簇类结构的研究,这些基于秘密共享的方案得到广泛应用[11-13]。然而,传统的秘密共享方案[8,10-14]要求在密钥恢复阶段的节点间通信必须是安全的,因而节点间需要事先存在安全的通信连接;否则一旦通信内容被外部攻击者截获,会造成密钥的泄露。而使用对称多项式可以有效解决节点间预先安全连接问题[15]。目前,已经有很多基于对称多项式的WSNs密钥协商方案[15-17],如Liu在2013年[15]提出了一种基于对称多项式可验证密钥分发方案。该方案使用对称多项式及组合值作为share,每对用户可以在无需协商的情况下生成相互通信的密钥,即可解决安全连接问题。但是这些基于对称多项式的方案都是用于实现每对用户之间的密钥协商,而非组密钥协商。
综上所述,本文拟针对无线传感器网络的特点,提出一种基于秘密共享的组密钥协商方案,该方案不仅支持新用户的动态加入,无需在线可信第三方支持,而且消除了对节点间的预先安全连接的依赖。
2 相关知识
2.1 对称多项式的特性
对称多项式是满足 f(x,y)=f(y,x)的二元变量多项式,可以使用对称矩阵表示。t-1阶对称多项式可以表示为 f(x,y)=a00+a10x+a11xy+…+at-1,t-1xt-1yt-1。假设每个用户都有唯一公开标识符Uk,k为正整数。对于每对用户(Ui,Uj),对称多项式 f(x,y)满足 f(Ui,Uj)=f(Uj,Ui),故可以利用这一特性建立每对用户的共享密钥。
Liu在2013年[15]提出了一种基于对称多项式的可验证密钥分发方案。通过服务器S选取t-1阶对称多项式 f(x,y)后,为每个用户计算share如下:f(U1,y),f(U2,y),…,f(Un,y),再通过安全信道将share发送给用户。用户Uk获取的share为单变量多项式 f(Uk,y)。对于每对用户(Ui,Uj),Ui将Uj代入自己的单变量多项式share中,得出结果即为 f(Ui,Uj)。Uj也将Ui代入自己的单变量多项式share中,得出结果即为 f(Uj,Ui)。由于对称多项式的特性,故双方得出的值相同且不为别的用户所知。可以使用该值作为二者通信的会话密钥,实现双方的安全通信。
2.2 基于多项式的秘密共享
Shamir在1979年[8]中提出了基于多项式的(t,n)门限秘密共享方案:将一个秘密s分割为n个share,使得任意t个或t个以上的share可以恢复秘密s,而少于t个share无法恢复该秘密。方案包含一个系统发起方Dealer和n个用户,并包含以下两个阶段:
(1)Share分发阶段:该阶段主要由Dealer向用户发送share。Dealer首先在GF(p)上秘密选择一个t-1次多项式,f(x,y)=a0+a1x+a2x2+…at-1xt-1(mod p),其中p为大素数,秘密s=f()0;然后Dealer利用每个用户公开的标识符Ui(i=1,2,…,n)计算 f(Ui)作为share秘密分发给用户Ui。
(2)秘密重构阶段:k(k≥t)个用户相互交换share,并按如下方式恢复秘密:
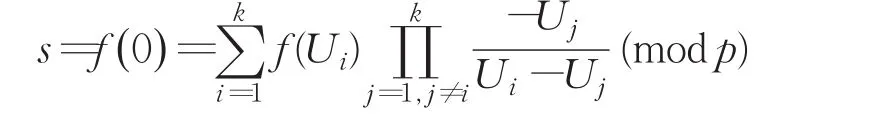
3 基于秘密共享的可更新组密钥协商方案
首先介绍组密钥协商方案的实体与安全模型;接着详细说明本文的方案,包括组内安全通信的建立,新用户的加入和组密钥更新机制。
3.1 实体与安全模型
(1)KM(Key Manager)
即密钥管理中心,在本方案中是可信安全的share分发管理实体。KM选取大素数p以及对称多项式等基本参数,同时计算并公布用于认证的单向Hash值H及哈希函数Hash(x)。本文假定用户可以在初始阶段安全获取share及H等信息。由于WSNs的特点,KM在向用户分发share后,不能保证与用户的通信。新用户加入前,最少有m个用户参与协商组密钥并建立了安全的组内通信。当新用户需要加入该组时,其与原先组内m个用户进行一次相互通信后,即可成为该组用户并更新组密钥,保证前向安全性。
(2)参与用户
即拥有有效share的用户。它们可以相互通信但部分通信信道有可能被截获。参与用户分为组内和组外两种用户:组内用户即已协商并共享组密钥的一组合法用户,组外用户指当前不属于该组的用户。所有参与用户需要通过share计算Component。本文的方案中包括两个阶段,第一个阶段是建立至少包含t个用户的初始安全组,共享一个组密钥;第二个阶段是新用户加入的阶段。新用户可以是原有持有share的组外用户,也可以是完全新加入的用户。这两个阶段都包括身份认证的功能,第一个阶段是对于所有用户的一次性认证;第二个阶段则原有组内用户会先接收新用户的Component并认证,通过后再发送自己的Component,以防止非法用户利用虚假信息获取Component相关信息。本文的方案中发送Component的过程无需同步进行。
(3)攻击者
主要考虑外部攻击者和内部攻击者两种情形。
外部攻击是指无合法share的用户截取相关信息进行破解或冒充新加入用户,最终达到获取组密钥的目的。
内部攻击主要有以下两种情况:①多个组内用户合谋获取组密钥,不向其他合法组内用户发送Component,从而将其他合法组内用户排除在组外,假定合谋者最多不超过t-1个;②多个组外合法拥有share的用户密谋获取KM选取的初始对称多项式的相关参数,通过不断加入组内获取足够多的Component,从而解出相关参数,进而伪造大量非法用户,并获取每对用户之间的私有通信密钥Sij。本文的方案限制新加入用户数最多为即最大用户数为其中m为初始的组内用户数,
3.2 组密钥协商方案
阶段1建立包含m个用户的初始组密钥
准备期:KM选取大素数 p、GF(p)上不相等的正整数c,d以及r0;在GF(p)上选取t-1次二元变量对称多项式F(x,y)和单向哈希函数Hash(x);初始参与用户数为m,满足KM为每个用户选取唯一标识符Ui。其中p,Ui,c,d都是公开的参数。
步骤1 KM为每个参与用户Ui计算share并安全发送:SHi=F(Ui,y)mod p;并将r0附在消息中。公布用于验证的单向哈希函数Hash(x)及哈希函数值:H=Hash(F(c,d ))mod p。
步骤2所有用户相互发送通信密钥加密过的Component。其中用户(Ui,Uj)之间的通信密钥Sij=F(Ui,Uj)mod p。Component记为Ci,Ci=F(Ui,c)mod p。
步骤3解密接收到的内容,获取所有人的Component后,恢复多项式F(x,c):
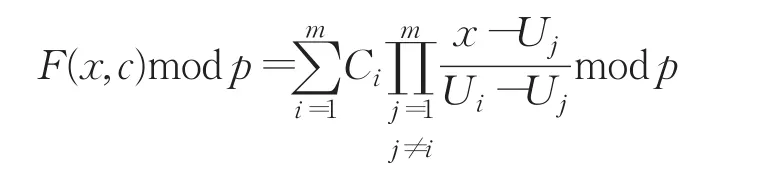
步骤4代入d值,得到F(c,d)mod p,计算其Hash值H′i。若H′i≠H 则协商失败;H′i=H 则通过验证,最终协商的组密钥S=(F(c,d)+r0)mod p。
阶段2新用户加入
准备期:新用户Uk的share为SHk=F(Uk,y)mod p。Uk并向组内所有用户发送使用通信密钥加密的Component:Ck=F(Uk,c)mod p;其中它与组内用户Uj的通信密钥Skj=F(Uk,Uj)mod p。
步骤1组内原有用户解密获取新用户的Component,结合阶段1中取得的所有原组内用户的Component再次恢复多项式F(x,c):

步骤2组内原有用户代入d值,得到F(c,d)mod p,计算其Hash值H″i。若H″i≠H 则新用户认证失败,拒绝加入;若H″i=H则身份认证成功,再将自己的Component加密后发送给新用户,并将r1=Hash(r0)附在消息中。新用户同理恢复多项式F(x,c),进而得到F(c,d)mod p。最终协商的组密钥S=(F(c,d)+r1)mod p。
阶段3组密钥更新
为了阻止新加入用户获得之前通信的内容,保证组密钥的前向安全性,方案需要组密钥更新的机制。由于本文的方案在新用户加入时先恢复F(c,d)mod p,所以更新组密钥仅需在此基础上做处理即可。
KM选取并公开单向函数Hash(x)。在阶段1初始m个成员协商组密钥时,可以在准备阶段由KM选取任意初始随机值r0,最终协商的组密钥S=(F(c,d)+r0)mod p。对于新加入的用户,将r1=Hash(r0)附在原有组内成员发给新成员的消息内。这种解决方案并没有增加额外的通信次数,当第i个用户加入时将ri附在消息中即可。其中ri=Hash(ri-1),新的组密钥为S=(F(c,d)+ri)mod p。
4 安全性,通信开销分析及方案特性总结
4.1 安全性分析
对于安全性分析,以假设攻击模型为主要方法,其中主要考虑外部攻击和内部攻击两种情形。
4.1.1 外部攻击
在方案的阶段1,用户(Ui,Uj)之间相互发送的Component通过私有密钥Sij进行加密,故即使外部攻击者截取了相关信息,仍需要破解Sij才能获取Component,而Sij本质上是由KM秘密选取的对称多项式生成的,攻击者无法获得的。
外部攻击者可能冒充新加入的用户,但是由于无法通过原有用户的身份认证,所以得不到原有用户的回应,获取不了任何相关信息。
4.1.2 内部攻击
(1)多个组内用户合谋获取组密钥,不向其他合法组内用户发送Component,从而将其他合法组内用户排除在组外,假定合谋者最多不超过t-1个。与(t,n)门限秘密共享的原理相同,本方案可以抵御t-1个用户对组密钥的合谋攻击[8]。
定理1在本文方案中,即使t-1个内部合谋也无法获得组密钥。
证明 假设有t-1个内部用户μt-1={Ui|i=1,2,…,t-1}合谋获得组密钥。则此t-1个内部用户μt-1相互发送信息共享彼此的Component,随后使用方案中的方法恢复多项式F(x,c)mod p,尝试获得F(c,d)mod p的值。要恢复多项式F(x,c)=r0+r1x+r2x2+…+rt-1xt-1(mod p),μt-1必须计算得到 ri(i=0,1,…,t-1)的值。现在 μt-1利用 t-1个Component的值F(Ui,c)(i=0,1,…,t-1)求解 F(x,c)的系数 ri(i=0,1,…,t-1)如下:

由于矩阵是t×(t-1)的,故矩阵的秩为t-1。而系数ri共有t个,故解是无穷多的。因此无法求解ri(i=0,1,…,t-1)的具体值,所以无法合谋获得组密钥。
所以,即使t-1个内部用户合谋也无法获得组密钥。
(2)多个组外拥有合法share的用户密谋获取KM的初始对称多项式。每个组外用户的Component实质上就是一个包含初始对称多项式参数的方程,如果组外用户能够构造足够多的Component,就可能解出对称多项式的所有参数。从而拥有和KM相同的能力,能够伪造大量非法用户,并能够获取每对用户间的私有通信密钥Sij。本方案假定最多加入用户数为其中m为初始的组内用户数,定理2表明,即使个用户的Component也无法恢复初始对称多项式F(x,y)mod p。
定理2在本文方案中,即使个用户的Component也无法解出F(x,y)mod p。
证明 假设有个用户共享彼此的Component,要恢复多项式 f(x,y)=a00+a10x+a11xy+…+at-1,t-1xt-1yt-1(mod p),必须求解aij(i,j=0,1,…,t-1)的值。现在这些用户利用个Component的值F(Ui,c)可以得到如下方程组:

由于对称多项式的特性,满足aij=aji。故在上式左边共有个未知系数。与(1)中证明类似,-1个Component无法解出对称多项式F(x,y)mod p的所有参数。
所以-1个用户合谋无法解出F(x,y)modp。
4.2 通信与计算开销
本文的方案及其他基于秘密共享的方案[11,14-15]都要求m个用户在秘密恢复阶段相互发送信息,故通信次数均为m(m-1)次。但是当新用户加入时,由于现有方案缺乏有效的动态加入机制,需重新协商组密钥,此时需要m(m+1)次通信;而本文的方案仅需新用户同原组内m个用户各发送和接收一次消息即可,总的通信次数仅为2m。
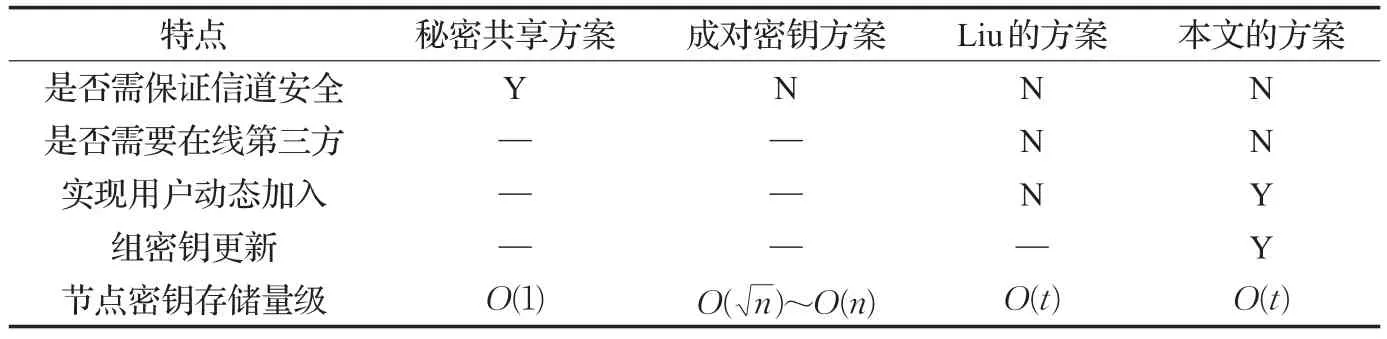
表1 方案特点对比表
在通信的计算开销上,主要考虑数据的加密和解密次数。相较于WSNs中成对密钥协商方案[5-6,15],组密钥方案在一对n的多播时,仅需使用组密钥加密一次数据即可。而成对密钥方案则需加密数据n次。此外多跳通信时(一对一),成对密钥方案要求每个接收节点解密并重新加密数据,n跳时共需分别加密和解密n次;而使用组钥方案仅需加解密一次。故本文的组密钥方案能够极大地减少多播通信以及多跳通信时的计算开销。
4.3 方案特性总结
本文方案具有以下特点:
(1)允许新用户的动态加入。本方案可以增加新的用户进入组内,并且仅需和原有用户进行一次相互通信过程即可,也可以认证新用户身份的合法性,解决了应用场景中所需要面临的问题。
(2)无需在线可信第三方。本方案能够在无在线可信第三方参与情况下完成组密钥的协商,并且可以一次性认证组内所有其他用户的合法性。KM仅需只是存在与方案的初始阶段,系统中用户从KM接收share后,无需再与KM进行任何交互。
(3)不需要提前保证通信信道安全。本方案应用对称多项式的特性,确保在组密钥协商阶段可以利用share与任何其他用户建立临时的安全连接,确保发送内容的保密性。
表1是和以前方案的对比,其中n是用户总数,t为基于秘密共享的门限,—表示不确定。
5 结束语
本文针对WSNs中节点动态加入和无在线可信第三方的需求,建立了基于秘密共享的组密钥协商方案。在本方案中,由KM选取share等基本信息,并在初始阶段安全地分发给参与用户。主要协商过程分为两个阶段,第一阶段是初始的m个用户通过share计算自己的Component并加密发送,随后通过恢复机制获取并认证组密钥,建立安全的组内通信环境。第二阶段是由新用户向组内用户发送加密后的Component,通过认证后获取组内用户的Component,并与组内用户协商建立新的组密钥。方案具有以下特点:(1)允许新用户的动态加入;(2)无需在线可信第三方;(3)不需要提前保证通信信道安全。在安全性上,由于使用了秘密共享的思想,可以抵御t-1个用户内部攻击。
[1]Shaikh F K,Zeadally S.Energy harvesting in wireless sensor networks:A comprehensive review[J].Renewable and Sustainable Energy Reviews,2016,55:1041-1054.
[2]Butun I,Morgera S D,Sankar R.A survey of intrusion detection systems in wireless sensor networks[J].IEEE Communications Surveys&Tutorials,2014,16(1):266-282.
[3]Eschenauer L,Gligor V.A key management scheme for distributed sensor networks[C]//Proc 9th ACM Conf Comp and Commun Sec,Nov 2002:41-47.
[4]Chan H,Perrig A,Song D.Random key predistribution schemesfor sensor networks[C]//Proc IEEE Sec and Privacy Symp,2003:197-213.
[5]Nirmala M B,Manjunath A S.Framework for pairwise key establishment in wireless sensor networks[C]//2014 InternationalConferenceon Contemporary Computing and Informatics(IC3I),2014:1070-1075.
[6]Rahman M,Sampalli S.An efficient pairwise and group key management protocol for wireless sensor network[J].Wireless Personal Communications,2015,84(3):2035-2053.
[7]Ruj S,Nayak A,Stojmenovic I.Pairwise and triple key distribution in wireless sensor networks with applications[J].IEEE Transactions on Computers,2013,62(11):2224-2237.
[8]Shamir A.How to share a secret[J].Communications of the ACM,1979,22(11):612-613.
[9]Wu B,Wu J,Fernandez E B,et al.Secure and efficient key management in mobile ad hoc networks[J].Journal of Network and Computer Applications,2007,30(3):937-954.
[10]Harn L,Lin Changlu.Authenticated group key transfer protocol based on secret sharing[J].IEEE Transactions on Computers,2010,59(6):842-846.
[11]Wu C,Li S,Zhang Y.Key management scheme based on secret sharing for wireless sensor networks[J].InternationalJournalofInformation and Communication Technology,2015,7(2/3):126-140.
[12]Hsu C F,Harn L,He T,et al.Efficient group key transfer protocol for WSNs[J].IEEE Sensors Journal,2016,16(11):4515-4520.
[13]Zhang Y,Wu C,Cao J,et al.A secret sharing-based key management in hierarchical wireless sensor network[J].International Journal of Distributed Sensor Networks,2013:1-7.
[14]Miao Fuyou,Xiong Yan.Randomized component and its application to(t,m,n)-group oriented secret sharing[J].IEEE Transactions on Information Forensics and Security,2015,10(5):889-899.
[15]Liu Y,Zhang Y,Harn L,et al.Verifiable symmetric polynomial-based key distribution schemes[J].Security and Communication Networks,2013,6(8):1028-1034.
[16]Haijun L,Chao W.An energy efficient dynamic key management scheme based on polynomial and cluster in wireless sensor networks[J].Journal of Convergence Information Technology,2011,6(5):321-328.
[17]Robinson Y H,Rajaram M.Establishing pairwise keys using key predistribution schemes for sensor networks[J].International Journal of Computer,Electrical,Automation,Control and Information Engineering,2015,9(2):608-612.
