单向纤维增强复合材料板I型裂纹尖端应力场的有限元分析

任 雷 盛冬发

(西南林业大学土木工程学院，云南 昆明 650224)

纤维增强复合材料是一种新兴材料，广泛地应用于航天航空、军工、汽车工业和建筑等重要领域。材料在服役期间，经常发生源于断裂或者终结于裂纹扩展的灾难性破坏事故，这些事故对人民的生命和财产造成重大损失。因此，对其断裂力学性能的研究具有重要的理论意义和应用前景，引起材料科学和力学界研究者的广泛兴趣。1965年，Shi等[1]已经给出了各向异性材料裂纹尖端应力场的解析解，应力强度因子 (K) 和裂纹与材料主方向的夹角决定了各向异性材料裂尖应力场的强度。各向异性与各向同性的不同在于裂纹不一定沿其初始方向自相似扩展。国内学者邵卓平[2]在2012年研究了木材的裂尖应力场，预测木材的裂纹将沿着顺纹方向扩展。Gregory等[3]研究了各向异性和双轴向远场载荷对单向离轴复合材料裂纹扩展方向的影响，分别采用正应力比理论、应力多项式理论和应变能密度理论分析了裂纹尖端应力场和裂纹扩展方向，理论上预测裂纹扩展方向与实验结果进行比较，得出正应力比准则能正确预测裂纹扩展方向。张少琴等[4-5]对含裂纹碳纤维增强的复合材料层合板进行了裂纹扩展方向预测理论的研究，介绍了一种新的复合材料Z断裂理论，并对含I型裂纹正交异性功能梯度材料板的应力场和位移场进行理论分析，得到了正交异性功能梯度材料板裂纹尖端应力场、位移场和梯度应力强度因子的理论计算公式。本研究在理论分析的基础上，应用ABAQUS有限元软件分析了单向纤维增强复合材料板I型裂纹尖端附近的应力场，预测了裂纹的扩展方向并对影响裂纹扩展的因素进行讨论。

1 研究方法

含一条裂纹长为2a的无限大正交各向异性板见图1，受对称荷载σ的作用。参考文献 [6]，由应变应力关系，在理论上分析裂纹尖端附近应力场。

图1正交各向异性I型裂纹板
Fig.1 Mode I crack of orthotropic plate

1.1 坐标轴平行于弹性主方向时裂尖应力场

当图1所示的坐标轴平行于弹性主方向时，板的应变应力关系为

(1)

式 (1) 中柔度矩阵 [b] 中的柔度系数为：

利用式 (1)，可得I型裂纹尖端附近应力场公式为：

(2)

式中：s1，s2为板关于弹性主方向坐标系X-Y的特征根，且满足：

b11s4+(2b12+b66)s2+b22=0

(3)

1.2 坐标轴不平行于弹性主方向时裂尖应力场

当坐标轴不平行于弹性主方向时，板的应变应力关系为

(4)

式 (1) 中的柔度矩阵 [b] 与式 (4) 中的柔度矩阵 [a] 之间满足：

(5)

式中：[T]ε为变换矩阵，且：

式中：β为X轴与材料第一弹性主方向夹角。

利用式 (4)，可得I型裂纹尖端附近应力场公式为：

(7)

式中：μ1，μ2为板关于非弹性主方向坐标系X-Y的特征根，且满足：

a11μ4-2a16μ3+(2a12+a66)μ2-2a26μ+a22=0

(8)

1.3 I型裂纹应力强度因子

根据有限大矩形平板I型裂纹应力强度因子可表示为[7-8]：

(9)

式中：C为修正系数，可取C为：

(10)

2 有限元分析

在理论分析的基础上，建立二维有限元模型，应用ABAQUS软件计算与材料纤维方向成不同夹角的裂纹裂尖应力场，并利用裂尖附近应力值对裂纹扩展方向进行预测。有限元模型选用含中心裂纹的单位厚度平板拉伸试件 (图2)，结合模型的尺寸与受力情况，可将其简化为平面应力问题，均选取裂纹上尖端进行分析。

2.1 裂纹尖端应力场

材料参数为：E1=12 GPa、E2=1.2 GPa、ν12=0.4、G12=G13=495 MPa、G23=85 MPa。纤维方向抗拉强度σ1=95.54 MPa，垂直纤维方向抗拉强度σ2=3.8 MPa。试件尺寸L=100 mm、2W=50 mm、2a=10 mm，左端固定，右端施加水平向右均布荷载为2 MPa，裂纹位于中间，纤维方向与裂纹方向夹角β分别为0°、30°、60°、90°。有限元分析所用单元类型为八节点双二次平面应力四边形单元，裂尖处采用退化的1/4奇异等参元，奇异单元半径为0.012 5 mm。

Mises应力是综合了3个主应力的一种等效应力，当受力物体内一点的Mises应力达到某一定值时，材料就进入塑性变形。应用ABAQUS有限元分析软件得出的4种裂纹试件的裂尖Mises应力场云图见图3，裂尖附近的Mises应力均在纤维方向达到最大。

图2 有限元分析模型Fig.2 Finite element analysis model

图3 4种裂纹试件裂尖附近的Mises应力云图Fig.3 The Mises stress nephogram around crack tip of 4 species

为了更直观的反映裂纹尖端附近的应力分布情况，裂纹尖端正前方与裂纹面垂直的应力σY和平行于裂纹面的应力σX的分布图见图4。

由图4可知，距离裂尖较近的范围内应力集中很明显，应力随着裂尖距离增大迅速减小。

图4裂尖正前方的σX和σY分布(θ=0°)
Fig.4 The distribution ofσXandσYfrom crack tip to up (θ=0°)

2.2 开裂方向预测

Buczek等[9]在预测复合材料裂纹扩展方向的研究中发现，裂纹将沿着裂尖附近以裂尖为心圆周上 “切向比正应力” 最大的方向扩展，被称为 “切向比正应力准则”。裂尖附近任一角度θ处沿着圆周切线方向的材料强度为：

Tθ=Asin2(β-θ)+Bcos(β-θ)

(11)

切向正应力为：

(12)

式中：A，B分别为材料1，2主方向上材料的抗拉强度；β为纤维方向与裂纹方向的夹角 (图5)。

图5 切向正应力示意图Fig.5 Illustration of tangential normal stress

“切向比正应力” 定义为：

(13)

3 影响裂纹扩展的因素

3.1 裂纹方向与纤维方向之间夹角β对裂纹扩展的影响

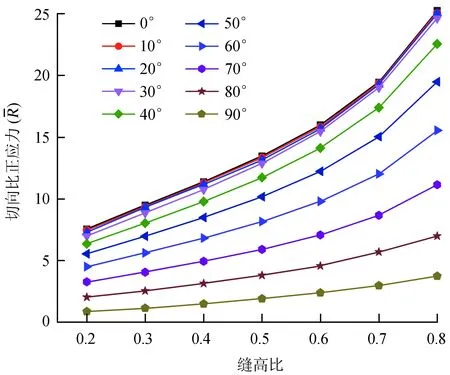
3.2 缝高比对裂纹扩展的影响

4 结 论

本研究建立二维有限元模型，分析了与材料纤维方向成不同夹角的裂纹裂尖应力场和切向比正应力，并对裂纹方向与纤维方向夹角和缝高比对裂纹扩展的影响进行了讨论。计算结果和实际情况吻合较好，得出如下结论：

1) 裂尖附近Mises应力在材料纤维方向达到最大。

2) 裂尖附近应力集中现象明显，应力随着裂尖距离增大迅速减小。

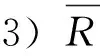
4) 纤维方向与裂纹方向夹角越小，裂纹越容易扩展。

5) 缝高比越大，裂纹容易扩展。

[1] Sih G C, Paris P C, Irwin G R. On cracks in rectilinearly anisotropic bodies[J]. International Journal of Fracture Mechanics, 1965, 1(3): 189-203.

[2] 邵卓平. 植物材料 (木、竹) 断裂力学[M]. 北京: 科学出版社, 2012.

[3] Gregory M A, Herakovich C T. Predicting crack growth direction in unidirectional composites[J]. Journal of Composite Materials, 1986, 20(1): 67-85.

[4] 张少琴, 杨维阳. 碳纤维增强复合材料板中I型裂纹扩展方向预测理论研究[J]. 应用数学和力学, 2004,25(6): 653-660.

[5] 张少琴, 杨维阳, 张克维. 功能梯度材料板I型裂纹的断裂力学研究[J]. 太原理工大学学报, 2005, 36(4): 470-473.

[6] 杨维阳, 李俊林, 张雪霞. 复合材料断裂复变方法[M]. 北京: 科学出版社, 2005.

[7] Horstman R, Peters K A, Meltzer R L, et al. A summary of fracture mechanics concepts[J]. Journal of Testing & Evaluation, 1983, 11(1): 56-65.

[8] 中国航空研究院. 应力强度因子手册[M]. 北京: 科学出版社, 1981.

[9] Buczek M B, Herakovich C T. Direction of crack growth in fibrous composites[J]. Mechanics of Composite Materials, 1983: 75-82.