全局弱式无网格方法求解消声器横向模态

赵 辉，左继强，刘成洋，方 智

（1.华中科技大学 船舶与海洋工程学院，武汉 430074；2.中国舰船研究设计中心，武汉 430064）

求解消声器横向模态常用的方法有解析方法和数值方法。解析方法[1]求解简单、快速、精确，但是仅局限于有解析方程的横截面，比如圆形截面，矩形截面以及椭圆形截面。对于任意形状的横截面横向模态的求解，只能使用数值方法[2]，现在较为成熟的常用的数值方法为二维有限元方法（FEM）和边界元方法(BEM)。该类方法均需要依赖于网格进行求解，是基于网格的求解方法。无网格方法(MFM)[3]是一种相对较新的数值方法，该方法不需要划分网格，采用基于点的近似，利用一组散布在问题域中以及域边界上的节点表示该问题域及其边界。无网格方法最先在力学领域应用较多，近十几年开始在声学领域被应用。无网格法对声学问题的求解，主要集中在对波动方程（Helmholtz方程）和线性欧拉方程的求解。1998年，Bouillar[4]应用基于移动最小二乘的无网格伽辽金法计算了二维内部声学问题，数值算例比较结果表明该方法比有限元法的计算精度高，计算速度快。2002年，Chen等应用边界配点的无网格方法计算了二维声腔的声学特征值问题，并指出该方法较有限元法简单，容易实施[5]。2010年，大连理工大学的张宏伟等应用基于点插值的配点型无网格法求解了Helmholtz方程，通过数值算例比较证明了该方法具有较高的精度和良好的收敛性[6]。2011年，湖南大学的姚凌云等将分区光滑径向点插值无网格法应用于二维声学分析中，对管道和二维轿车声学问题的数值分析结果表明，该方法比有限元法具有更高的精度[7]。2012年，海军工程大学的胡海等将边界无网格法应用到结构声辐射计算中，通过与解析结果对比表明该方法具有更高的插值和计算精度[8]。华中科技大学的黄其柏课题组将径向配点无网格法应用到气动声学和腔体结构声学的研究中，取得很好的成果[9]。2016年，曾向阳等提出一种基于声粒子分布积分的无网格数值算法计算小尺度封闭空间中低频声场的数值方法，指出该方法特别适用于飞机座舱等关注中频段声场分布的情况[10]。2017，方智等提出应用强式无网格配点方法耦合模态匹配技术计算任意横截面膨胀腔消声器的传递损失，计算结果与实验测量值吻合较好，且计算速度较三维有限元方法具有一定的优势[11]。但当导数边界条件较多时，使用强式无网格配点方法求解消声器横向模态稳定性会变差。

本文基于无网格方法本身的优势，使用径向基函数点插值法离散本征方程，应用伽辽金加权残数法进行数值积分，构成全局弱式无网格方法用来求解消声器横向本征波数以及模态形状，更方便添加导数边界条件。进而分析研究形状参数对计算精度和速度的影响。

1 全局弱式无网格方法求解横向模态

图1为任意形状等截面直通穿孔管阻性消声器示意图，将其分为三个区域：进口管A、膨胀腔C和出口管E，对应的横截面分别为S1、S3=S1+S2和S1。膨胀腔被穿孔管分为两部分：C1和C2，对应的横截面分别为S1和S2，C2内填充吸声材料。

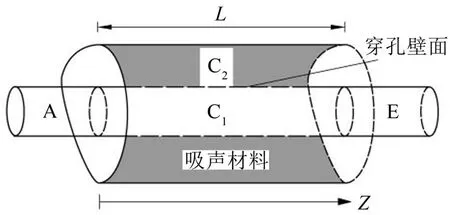
图1 任意形状等截面直通穿孔管阻性消声器

以膨胀腔C为例，介绍全局弱式无网格方法求解横向模态的基本思想。膨胀腔内横向声压控制方程满足以下形式

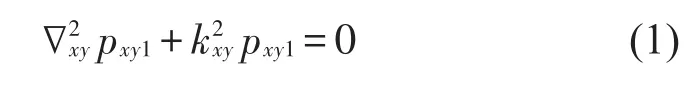
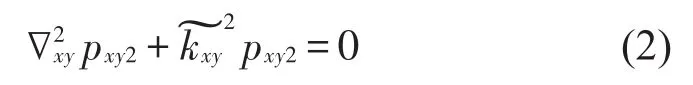
其中：为二维直角坐标系下的拉普拉斯算子，pxy1和pxy2分别为区域C1和C2内的横向声压分量，kxy和分别表示空气和吸声材料中的横向波数，并且满足以下关系

其中：kz为轴向波数k=ω/c0为空气中的波数，ω为圆频率，c0为空气中的声速，=ω为吸声材料中的复波数，为吸声材料中的复声速。

穿孔膨胀腔的边界条件可以表示为以下形式，外部环形腔刚性壁边界条件

穿孔面边界条件

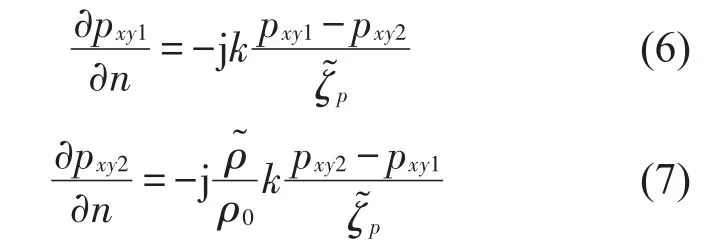
其中：ρ0为空气密度为多孔吸声材料密度为一侧有吸声材料时穿孔结构的特性声阻抗率

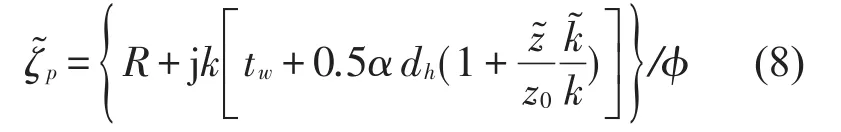
其中：ϕ为穿孔率，z=ρ0c0和分别空气和吸声材料的特性阻抗。为单个孔的特性声阻，μ为动力黏度系数，tw为穿孔管厚度，dh为穿孔孔径，α为单孔厚度修正系数，可以表示为[12

其中：各个参数的含义可参考文献[12]。

1.1 无网格径向基点插值法求解形函数

为了避免采用多项式基PIM所引起的奇异性问题，径向基函数（RBF）被采用以形成径向基点插值法（RPIM）形函数用于弱式无网格法。添加多项式的RPIM插值可以表示为

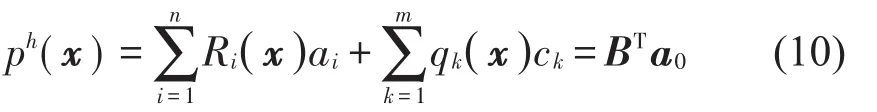
其中：Ri(x)为径向基函数，n为RBFs的个数，qk(x)为空间坐标xT=[x,y]中的单项式，m为多项式基函数的个数。

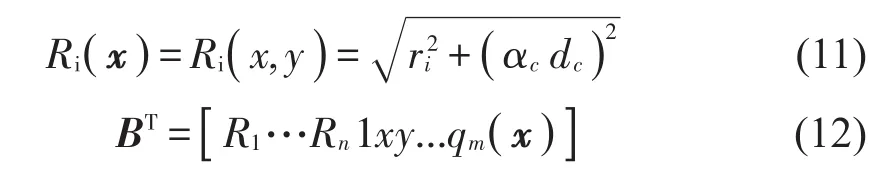
为了确定系数矩阵中的ai和ck，需要形成计算点x的支持域，其中包括n个场节点。支持域的大小由ds=αsdc确定，αs为支持域的无量纲尺寸，应该由分析者事先确定，dc为计算点x支持域内的平均节点间距。在径向基函数Ri(rk)中，αc为形状参数。第i个场节点和第k个场节点之间的距离rk为

使方程满足计算点x周围的n个节点值，一个节点对应一个方程，将产生n个线性方程。求解以下方程即可得到系数矩阵a0。

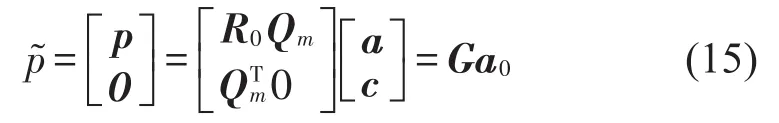
其中，各个矩阵表达式如下

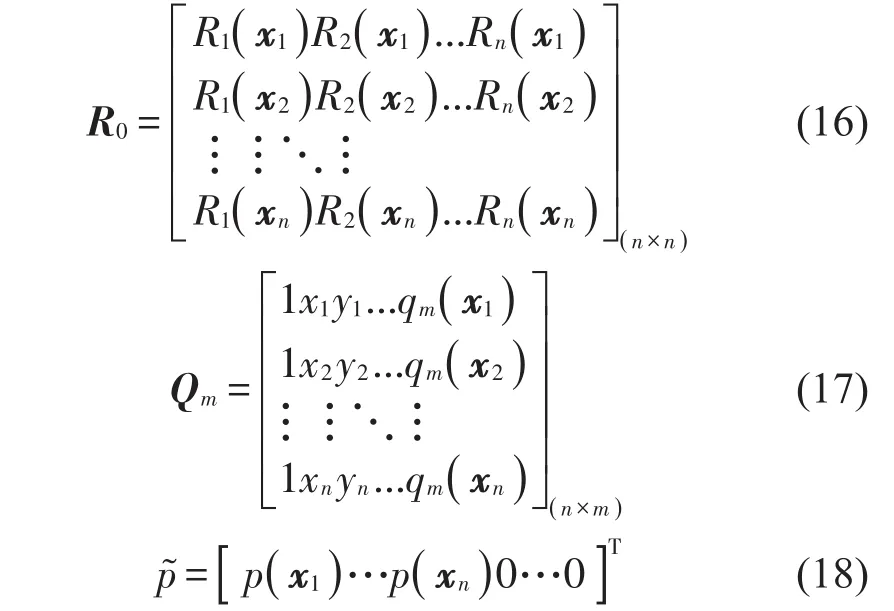
很明显，矩阵G是对称矩阵，所以其可逆，因此系数矩阵a0可以由方程求得

将系数矩阵代入到方程，可以得到

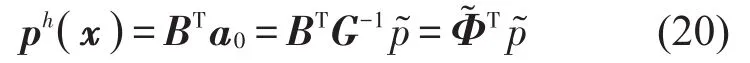
对应节点声压向量的RPIM形函数Φ表达式为

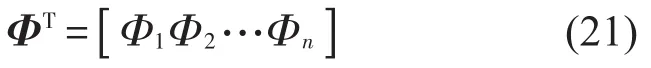
最终，横向声压ph()x可以表示为

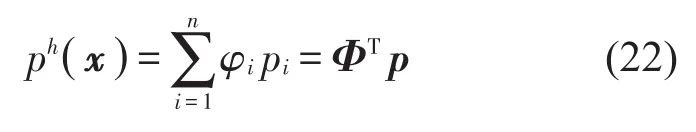
1.2 基于Galerkin弱式离散系统方程

应用加权残数法构造横向本征方程和边界条件的弱式无网格形式。采用伽辽金加权残数方法，权函数和形函数选取一致，如同式(21)所示。本征方程和边界条件的残数乘以权函数并且在各自域内积分，可以得到加权形式

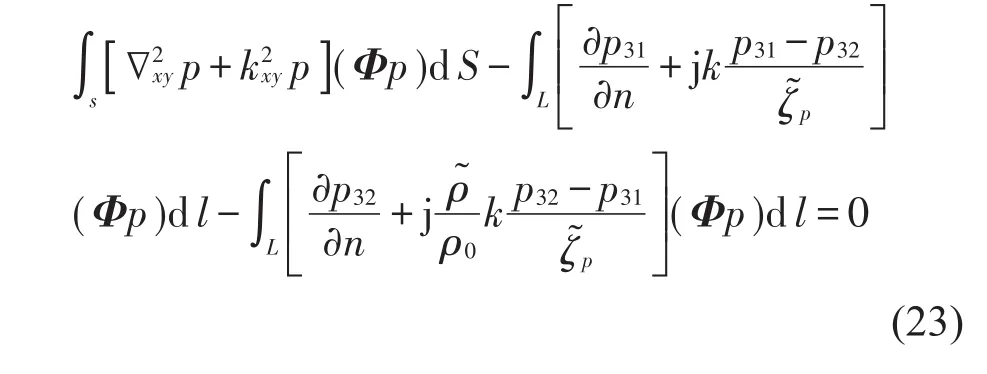
应用格林公式，方程简化为以下线性方程

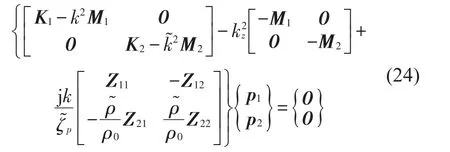
其中：K1,M1,Z1，K2,M2,Z2分别为横截面S1和S2内的广义刚度矩阵、质量矩阵和穿孔阻抗矩阵。为了求解这些系统矩阵，需要求解域内和边界上的积分。因此在弱式无网格方法中需要构造背景网格。背景网格与场节点是相互独立的，并且对网格质量没有太高要求。

在每一个背景网格单元中配置高斯点，对于每一个高斯节点形成支持域，求解每一个高斯点的形函数Φ，进而计算背景网格单元的刚度矩阵，质量矩阵以及阻抗矩阵。

其中：nQ为单元e内的高斯点个数，wQ为相应的高斯加权系数，Je为单元的雅克比矩阵。

在弱式无网格方法中，背景网格单元一般选取规则形状，四边形或者三角形。在本文中，采用四边形单元，每个单元中高斯点取4个。

对于不含有穿孔的横截面，穿孔阻抗等于零，化简方程可以求得横向本征方程为

求解式(24)和式(28)可以求得穿孔横截面和非穿孔横截面的横向模态。

1.3 求解本征方程

假设横截面上的节点数为n，通过式和可以分别求得膨胀腔和进出口管道轴向波数向量kz和特征向量矩阵Xxy，其中kz的维数为n，Xxy的阶数为n×n。横向节点声压分量组成的向量可以表示为，其中φ代表模态幅值系数组成向量，其维数为n，i为模态阶数。

横向声压分量可以表示为

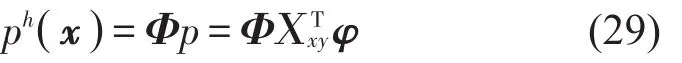
最终，可以得到本征函数的表达式为

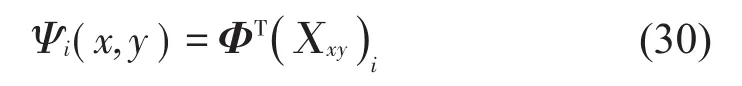
2 计算精度与效率验证

为了验证本文方法的计算精度和效率，本文计算了圆形截面，不规则截面和穿孔截面的本征横向波数。计算结果分别与有限元结果和解析结果进行对比，本征值的相对误差被定义为如下形式

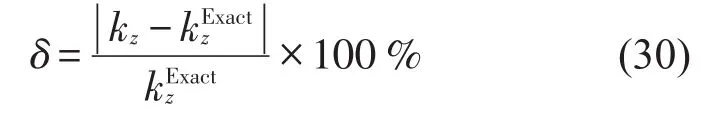
2.1 圆形截面

因为规则横截面有横向本征波数的解析解，所以如图2所示的圆形截面最先被分析，圆形截面半径为r=0.0245 m。截面内的场节点的分布是通过简单的MATLAB程序构造的，背景网格由商业软件ANSYS得到。由图2可以看出，场节点是任意分布的，与背景网格是相互独立的。

图2圆形横截面内任意分布的场节点和背景网格

图3 给出了分别使用全局弱式无网格方法和有限元方法计算的前5阶本征波数的相对误差值。

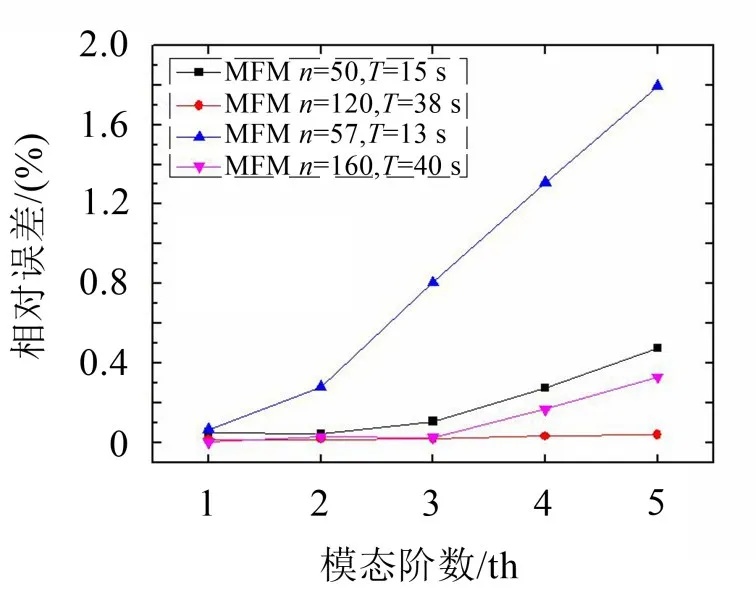
图3 圆形截面本征值计算结果比较

由图可以看出，随着横截面内节点数的增加，仿真结果与解析结果的误差逐渐减小。在无网格方法中，节点数为50时，相对误差可以控制在0.5%以内，需要的计算时间为15 s，而在有限元方法中，节点数为57时，第5阶模态的本征值相对误差为1.8%。为了将前5阶模态本征值的相对误差控制在0.5%以内，在有限元方法中需要160个节点，计算时间为60 s。

2.2 非规则截面

为了证明本文方法的适用性和准确性，本小节计算了如图4所示的非规则截面的本征值。四边形的具体尺寸如图上所标，长度单位为m。

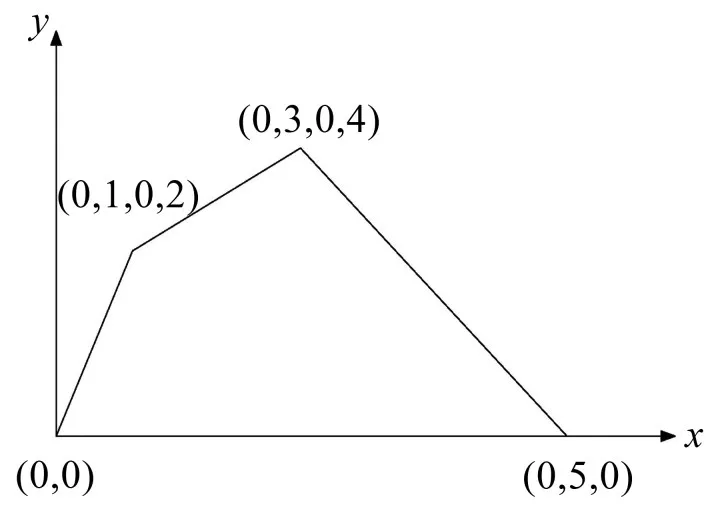
图4 非规则四边形横截面

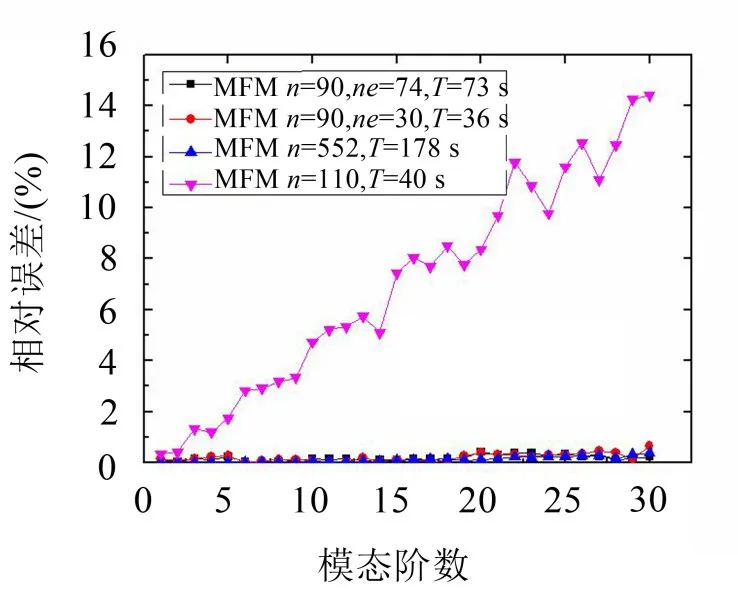
图5 不规则四边形截面本征值计算结果比较

由于该截面为非规则截面，其本征频率没有解析解。本文采用二维有限元方法和无网格方法计算其前30阶本征频率。在有限元方法中，随着划分节点数的增多，计算精度增高，经计算得知，当节点数取522时，再增加节点数，精度增大不大，图线中给出了节点数取1000和522时，前30阶本征频率仿真值的相对误差均在0.5%以内，说明有限元方法中节点数取522，可以得到较高的计算精度，需要耗时178 s。为得到相同精度的本征值，无网格方法中需要节点数为90。若背景网格单元采用有限元方法形成，即每一个节点都被包含在单元中，背景网格单元数为74，计算本征值所需时间为73 s。由于无网格方法对单元的依赖性较小，背景网格单元可以任意生成，本文中针对本算例采用30个单元作为背景网格，可以得到相同精度的本征值计算结果，所需时间为36 s，时间减少一半。为了对比，图中给出了有限元方法中节点数取110时的本征值的相对误差，相对误差随着节点数的增加基本呈增大趋势，在第10阶本征值以后，相对误差超过5%，计算结果不再精确。

2.3 圆形穿孔截面

为了进一步验证本文全局弱式无网格方法的适用性和准确性，本小节研究了如图6所示的圆形穿孔截面。横截面的具体尺寸为：穿孔管直径d=0.0249 m，膨胀腔直径D=0.1644 m。

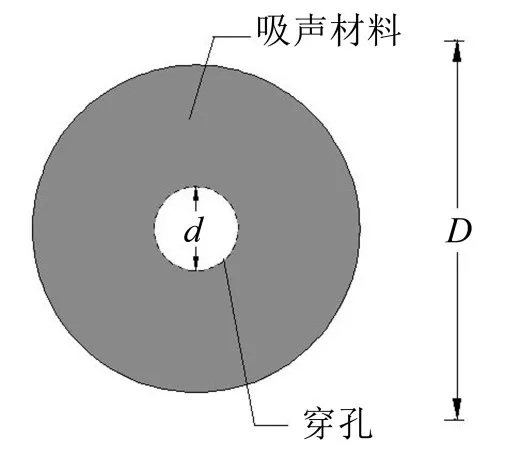
图6 圆形穿孔阻性消声器横截面

在本文中所用吸声材料为玻璃丝绵，密度为100 g/L。其特性声阻抗和复波数的表达式为[14]

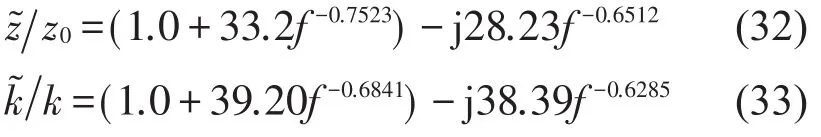
由公式可知，每一个激发频率都有相应的本征值，即轴向本征波数。本文计算了激发频率为3000 Hz时前5阶径向模态的轴向本征波数，表1中给出了分别使用解析方法，二维有限元方法和本文无网格方法计算的本征值，可以看出达到一定的精度，有限元方法需要1600节点构成八节点四边形单元，需要时间为445 s，而无网格方法只需140个节点，需要耗时75 s即可达到相同的精度。

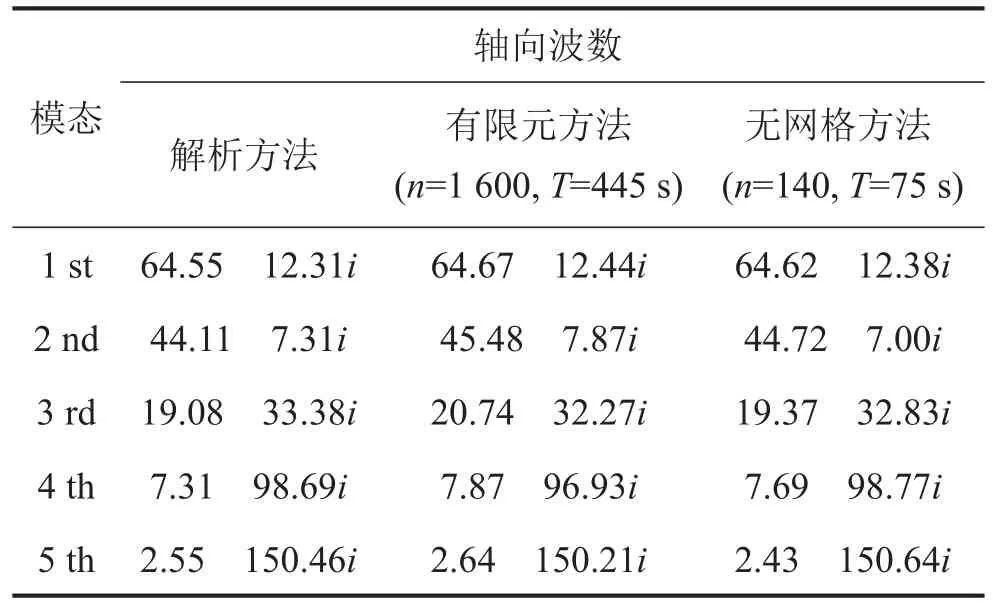
表1 圆形穿孔阻性消声器横截面的轴向本征波数

通过以上3个算例可以看出，相对于有限元方法，无网格方法求解横截面本征模态，不依赖于网格，需要的节点更少，耗时更少。横截面面积越大，边界条件越复杂，无网格方法的优势就越突出。

3 计算结果与分析

由前面分析可以知道，每个计算节点支持域的尺寸由形状参数αs决定，图7分析了支持域尺寸对本征值计算精度的影响。

由图7可以看出，在低频段内计算本征值，支持域大小对计算结果影响不大，随着计算频率的增高，支持域的影响越来越明显。随着支持域逐渐增大，相对误差整体趋势逐渐变小，当支持域的大小达到一定尺寸，相对误差变化不大。针对本文中所有算例，支持域的大小取2.5倍dc时，计算前30阶本征值误差控制在0.5%。但是计算时间会随着支持域尺寸的增大而增多，所以支持域尺寸的确定需要考虑计算精度和计算速度之间的平衡。

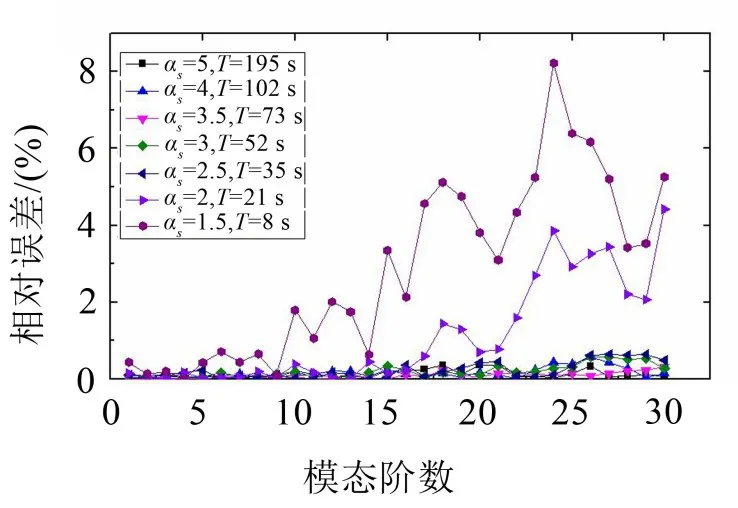
图7 支持域尺寸对计算精度的影响

径向基函数中另外一个形状参数为αc。图8给出了αc取7种不同数值时，非规则四边形截面前30阶本征频率的相对误差。

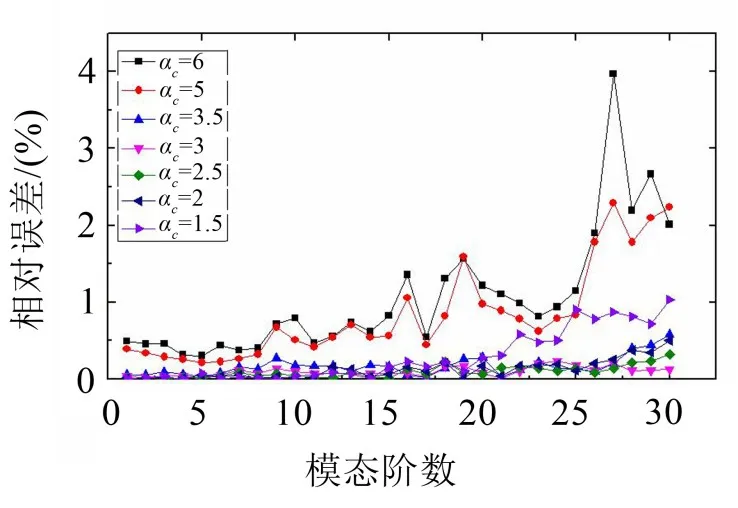
图8 形状参数αc对计算精度的影响

从图中可以看出，在低频段内形参αc对本征值计算精度影响不大，随着计算频率增大，影响逐渐明显。在整体频率范围内，αc值取太小或太大都会使得相对误差增大，这是因为矩阵条件数变大使得计算结果不稳定的原因。针对本文所有算例，αc取值2～3.5之间计算本征值可以取得较高的精度。

4 结语

采用全局弱式无网格方法提取消声器横向本征值（横向波数）和本征向量（声压模态），使用径向基函数点插值方法用来离散本征方程，使用伽辽金加权残数法用来数值积分，最终求得消声器横向本征函数。通过计算圆形截面，非规则四边形截面和穿孔阻性消声器横截面的本征波数，分别与解析方法和有限元方法计算结果进行对比，验证了全局弱式无网格方法求解消声器横向本征模态具有较高的精度，并且需要更少的节点和计算时间。当支持域尺寸大于2.5倍dc时，形状参数αc在2～3.5之间取值时，计算得到的本征值精度较高。

与有限元方法相比，无网格方法中背景网格不依赖于节点，在计算过程中可以随意添加会删除某些节点，这也是其优势所在。

[1]SELAMET A,XU M.B,LEE I-J.Analytical approach for sound attenuation in perforated dissipative silencers with inlet/outlet extension[J].J.Acoust.Soc.Am.,2005,117(4):2078-2089.

[2]ZHAO S.On the spurious solutions in the high-order finite element methods for eigenvalue problems[J].Comput MthodAppl.M.,2007,196(49-52):5031-5036.

[3]LIU G R,GU Y T.An introduction to meshfree methods and their programming[M].New York:Springer,2005.

[4]BOUILLARD P,SULEAUB S.Element-free Galerkin solutions for helmholtz problems:formulation and numerical assessment of the pollution effect[J].Comput MthodAppl.M.,1998,162:317-335.

[5]CHEN J T,CHANG M H,CHEN K H,at al.Boundary collocation method for acoustic eigen analysis of threedimensionalcavities using radialbasis function[J].Comput Mech.,2002,29(4):392-408.

[6]李美香，张宏伟，李卫国.基于点插值的配点型无网格方法解 Helmholtz问题[J].计算力学学报，2010，27（3）：533-536.

[7]姚凌云，于德介，臧献国.声学数值计算的分区光滑径向点插值无网格法[J].振动与冲击，2011，30(10)：188-192.

[8]胡海，郭文勇，马龙.结构声辐射计算的边界无网格法[J].噪声与振动控制，2012，32(5)：37-41.

[9]LI K,HUANG Q B,WANG J L,LIN L G.An improved localized radialbasisfunction meshlessmethod for computational aeroacoustics[J].Eng.Anal.Bound Elem.,2011(35):47-55.

[10]曾向阳，王海涛，杜博凯.基于声粒子分布积分的无网格声场计算方法[J].应用声学，2016，5（1）：84-89.

[11]FANG Z,LIU C Y.Combined mesh free method and mode matching approach for transmission loss predictions of expansion chamber silencers[J].Eng.Anal.Bound Elem.,2017(84):168-177.

[12]I Z L,FANG Z.On the acoustic impedance of perforates and its application to acoustic attenuation predictions for perforated tube silencers[C].Inter-noise 2011,Osaka,Japan,September,2011.

[13]方智，季振林.穿孔管阻性消声器横截面模态及消声特性计算与分析[J].振动与冲击，2014，33(7)：138-146.