基于传声器阵列的汽车鸣笛声定位算法及实现
2018-06-25张焕强黄时春蒋伟康
张焕强,黄时春,蒋伟康
(上海交通大学 振动、冲击、噪声研究所 机械系统与振动国家重点实验室,上海 200240)
近年来,随着中国经济的快速发展,汽车逐渐成为人们生活与工作中不可或缺的重要组成部分,各大城市的机动车数量逐年增加。汽车保有量的增多也带来了日益严重的交通噪声污染问题,尤其是汽车鸣笛声对市民的日常生活影响较大。公安部门颁布了相应的法规来限制或禁止某些路段的汽车鸣笛声,交警部门常采取巡逻纠违等方式对汽车鸣笛声加以监管,但人工执法的方式存在执法效率低,可靠性不高的缺点。而基于传声器阵列的声源定位技术可以帮助交通执法部门快速准确地锁定违章鸣笛车辆的方位。
基于传声器阵列的声源定位技术可分为3类[1]:基于最大输出功率的可控波束形成法、高分辨率谱估计法和基于到达时间差(TDOA)的声源定位法。基于最大输出功率的可控波束形成方法是对传声器接收到的信号进行加权求和,直接控制传声器指向具有最大输出功率的方向,该方法可以用于多声源的定位,但是存在对初值敏感以及需要背景噪声等先验知识的问题;基于高分辨率谱估计的方法利用传声器信号之间的相关矩阵来确定方向角,可以对声源方向进行有效的估计,但计算量比较大;基于到达时间差的声源定位方法先求出声信号在不同传声器的时间差,将时间差转化为声程差后用几何法或搜索法确定声源位置。该方法原理简单,计算量小,易于保证声源定位的实时性,故本文研究基于到达时间差的声源定位方法对汽车鸣笛声进行定位。
基于到达时间差的声源定位算法主要由两部分组成。第一部分是时间延迟估计(TDE),确定传声器阵列中不同的传声器对同源声信号的到达时间差(TDOA);第二部分是根据第一步估计出的时间延迟,转化为对应的声程差,结合传声器阵列中的传声器位置,通过特定的声源定位算法计算得到声源的位置。时延估计技术又有很多方法,包括广义互相关(GCC)方法[2],自适应最小均方(LMS)方法[3–4],基于空间的特征值分解(EVD)方法[5]以及基于传递函数比(ATF-s ratio)的方法[6]等。其中,广义互相关方法原理简单,具有一定的抗噪声及混响性能,能够保证估计的实时性,本文中采用此方法进行时延估计。
1 鸣笛声检测
本文研究的声源目标为汽车鸣笛声,汽车鸣笛喇叭主要分为电喇叭及气喇叭两类,城市道路上大多数车辆安装的喇叭为电喇叭。电喇叭又分为单音喇叭、双音喇叭、三音喇叭等几类,汽车喇叭发出的鸣笛声是基频范围在240 Hz~650 Hz的短时且指向性不明确的平稳信号[7]。
鸣笛声的检测与识别模块可以由信号滤波、分帧加窗、端点检测以及鸣笛声识别等四部分组成[8],本文仅研究已有信号的鸣笛声检测及定位问题。对于一段含有鸣笛声声的信号,要对其进行定位,首先要确定喇叭信号的位置,即端点检测。目前有很多成熟准确的端点检测算法,如双门限法、短时能量法、短时过零率法以及自相关法等方法。本文研究的定位算法中,端点检测部分采用的是短时能量法,见式(1)。

式中:x(m)为传声器测量信号,w(n-m)为所加的窗函数,En为第n帧的短时能量。根据测量信号中噪声信号与鸣笛声信号能量的不同,设定一定的门限,即可获得鸣笛声的开始及结束端点,而环境噪声的能量则需要根据路段的不同进行实验获得。
2 鸣笛声定位算法
2.1 时延估计算法
传声器阵列中任意两个传声器i和j接收到的信号可用以下模型来表示
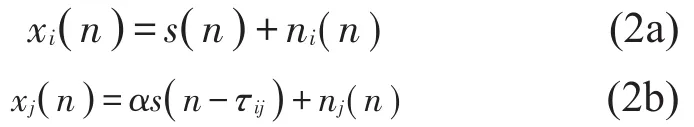
式(2)中:s(n)为传声器i处接收到的声源信号ni(n)与nj(n)分别为传声器i和j接收到的噪声信号,τij为传声器i和j之间的时间延迟,α为两个传声器检测声信号的幅值比。设xi(n)和xj(n)的傅里叶变换分别为Xi(ω)和Xj(ω),两传声器接受信号的广义互相关函数Rij(τ)可表示为

式(4)中:φij(ω)为广义互相关加权函数,用广义互相关方法进行时延估计的框图如图1所示。

图1 广义互相关时延估计框图
针对不同的噪声和反射情况,可选择不同的加权函数φij(ω) 。当广义互相关的加权函数φij(ω) =1 |Gij(ω) |时 ,此时为互功率谱相位(CSP)时延估计方法。其中互功率谱密度函数为信号互相关函数的傅里叶变换

由式(4)可知,互功率谱相位法对功率谱函数进行了白化处理,仅保留信号的相位信息,使得广义互相关函数的峰值更加尖锐,具有抑制噪声和混响的能力,因此本算法中采用互功率谱相位(CSP)时延估计算法。
2.2 定位算法
自由场中单极子声源的传播方式为球面波
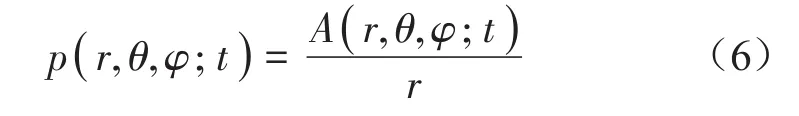
式(6)中:p(r,θ,φ;t)为在球坐标系位于(r,θ,φ) 点t时刻的声压。考虑在三维空间中布置传声器阵列定位汽车喇叭的鸣笛声,则声源与传声器阵列的不同传声器之间存在声程差,即声信号到达各传声器存在时间差。对汽车喇叭做点声源假设,设其笛卡尔坐标为(x,y,z),则理论上至少需要3个声程差才能求得空间中声源的位置。取传声器阵列的1号传声器为参考点,其余传声器与1号传声器之间存在如下几何关系

式(7)中:(xi,yi,zi)(i=1,2,3,4)代表第i个传声器的三维笛卡尔坐标,Δt1i代表第i个传声器与1号传声器之间的时间差。将上式的3个方程求平方并消去相同项可得

式(8)中:

重新整理式(8)可得[9]

式(9)中:

R为实际声源到1号传声器之间的距离,ai、bi、ci(i=1,2,3)为已知量,时延估计完成后,ei也为已知量。对于任意给定的R值,均可得出一组对应的假设声源坐标(x,y,z),结合传声器与假设声源坐标的位置关系可以得到麦克风阵列的任意2个传声器之间的时延计算结果,则构造目标函数:

式(10)中:Δt*ij为假定声源坐标与1号传声器距离为R时的时延计算结果,Δtij为通过时延估计算法得到的实际时延估计结果,N为阵列的传声器个数,当假定声源位置与1号传声器的距离与实际声源位置与1号传声器的距离最接近时,J取最小值,由此条件确定的R值,代入式(9)即可求得实际声源坐标(x,y,z)。给定不同的R值进行搜索属于一维搜索问题,实际在取值是可先给定较大的搜索间隔,得到声源的粗略估计结果,初步缩小搜索区域,再减小搜索间隔进行精细搜索,以减小搜索的计算量。
3 定位算法仿真
上述基于空间搜索的声源定位方法需要的传声器个数至少为4个,如果增加传声器的个数,则定位精度会有一定的提高,但考虑到实际鸣笛声定位系统的实际应用及实时性要求,不能无限制地增加传声器个数,因此需要在保证定位精度的同时使用较少传声器。

图2 传声器阵列布置图
下面以正4面体阵列为基本原型阵列,分别在该原型阵列上添加1至2个传声器,通过MATLAB分别仿真4传声器、5传声器和6传声器阵列的定位效果。仿真所用信号为基频为510 Hz的正弦倍频信号,采样频率102.4 kHz,同时加入30 dB的白噪声干扰。声源位置为随机产生的100个点,距离坐标原点距离范围5 m~20 m,每隔0.15 m产生一个声源距离值,仰角和方位角均为-60°~60°之间随机产生。传声器的布置如图2所示,6个传声器的坐标(单位:m)设置分别为S1(0.866,0,0)、S2(0,0.5,0)、S3(0,-0.5,0)、S4(0.2887,0,0.8165)、S5(0.2887,0,0)、S6(0.2887,0,0.4082)。其中1-4号为边长为1 m的正4面体的4个顶点,5号与6号传声器均布置在正4面体空间内。
图3、图4、图5分别表示当传声器个数分别为4、5、6个时的仿真误差结果图。图中各项误差指标的定义如下:
方位角估计误差为

仰角估计误差为

距离相对误差为

式(11)、式(12)、式(13)中的φ0、θ0及R0分别为已知声源理论位置时计算出的方位角、仰角及距离原点的距离。
由图3、图4及图5的仿真结果分析可得,4传感器阵列的方位角估计误差在1.5°之内,除个别点外,仰角误差均在2°之内,然而距离相对误差很大;5传感器阵列不论是从方位角、仰角还是相对距离方面均较4传感器阵列有较大提高;然而在5传感器基础上再增加一个传感器进行分析,各角度及相对距离没有较为明显的提升。在实际汽车鸣笛声定位系统的设计中,定位的主要目的是通过定位返回的结果控制安装在监控路段的摄像头,使其能够对准违章车辆。因此,我们更加关注方位角及仰角的估计精度,所以本算法中阵列采用在正4面体传声器阵列的基础上改进获得的5传声器阵列。
4 声源定位实验
为验证上述算法对汽车鸣笛声源定位的有效性,构建一个以正四面体阵列为原型,另添加一个传声器的5传声器阵列三维声源定位系统,选择一段马路上进行实车鸣笛声定位验证,实验中采用的车辆为五菱宏光S,旁边平行放置一辆五菱荣光车作为干扰,验证定位算法能否定位准确。实验现场如图6所示。

图3 4传声器阵列仿真误差图

图4 5传声器阵列仿真误差图

图5 6传声器阵列仿真误差图

图6 汽车鸣笛声源定位实验设置图
图6 中规定坐标系的X轴与汽车纵向轴线平行,且与汽车宽度方向中心线重合。Z轴竖直向上,Y轴则根据右手定则确定,图6中1-5标号为采用的5个传声器的布置位置,各传声器的三维坐标(单位:m)分别为 :S1(0 ,0,1.750) 、S2(0.341,0,1.335) 、S3(- 0.170,-0.295,1.312)、S4(- 0.170,-0.295,1.312)、S5(0.050,0.020,1.505)。鸣笛声信号经BBM数据采集仪进行记录,采样频率102.4 kHz,图7为鸣笛声实测信号。
在马路上标记6个测点,相对于规定原点的方向(仰角和方位角)如表1所示,即实际声源的方向范围。因为汽车上有两个喇叭,两个喇叭关于X轴对称,表1中显示的为两个喇叭相对于规定原点的方位角范围。而表1中仰角范围为地面和汽车最高点相对于规定原点的仰角值。其中汽车的高度为1.7 m。实际验证时,只要算法估计出的方向在给出的范围内即可认为声源准确定位到汽车上。

图7 实测鸣笛声信号

表1 5传声器阵列定位实验结果
在汽车鸣笛声定位算法的研究中,我们更加关注方位角及仰角的估计精度,而对距离的精度要求较低。分析比较表1展示的定位计算结果可知,基于空间搜索法的5传声器阵列三维声源定位算法在实验时能够将声源位置准确地定位在汽车上,能够有效的定位汽车鸣笛声。
5 结语
本文针对汽车鸣笛声的声源定位问题,提出了一种基于空间搜索法的五传声器阵列三维空间声源定位算法。采用短时能量法检测确定信号中的鸣笛声的端点位置,通过互功率谱相位时延估计算法估计任意传声器之间的时间延迟,运用空间搜索法来确定声源位置,实际定位的计算量不大且能够满足定位的实时性要求,能够快速且准确地锁定鸣笛车辆。
[1]BRANDSTEIN M S,SILVERMAN H F.A practical methodology for speech source localization with microphone arrays[J].Comput.Speech Lang,1997,11(2):91-126.
[2]KNAPP C,CARTER G.The generalized correlation method for estimation of time delay[J].IEEE Trans.Acoust.Speech Signal Process,2003,24(4):320-327.
[3]REED F A,FEINTUCH P L,BERSHAD N J.Time delay estimation using the LMS adaptive filter-Static behavior[J].IEEE Trans.Acoust.Speech Signal Process,1981,29(3):561-571.
[4]YOUN D,AHMED N,CARTER G.On using the LMS algorithm for time delay estimation[J].IEEE Trans.Acoust.Speech Signal Process,1982,30(5):798-801.
[5]BENESTY J.Adaptive eigenvalue decomposition algorithm for passive acoustic source localization[J].J.Acoust.Soc.Am,2000,107(107):384-391.
[6]GREENFIELD S,Clift M.Speaker localization in a reverberant environment[C].In Electrical and Electronics Engineers in Israel,2002.the Convention.2003:7-9.
[7]张志飞,袁琼,徐中明,等.汽车喇叭声特性试验分析[J]. 汽车工程学报,2013(6):400-404.
[8]孙懋珩,俞莹婷.汽车鸣笛声定位系统仿真[J].声学技术,2009(5):640-644.
[9]WU S F,ZHU N.Locating arbitrarily time-dependent sound sources in three dimensional space in real time[J].J.Acoust.Soc.Am.,2010,128(2):728.
[10]ABEL J,SMITH J.The spherical interpolation method for closed-form passive source localization using range difference measurements[C].In Acoustics,Speech,and Signal Processing,IEEE International Conference on ICASSP.1987:471-474.
