一种基于梯度下降的次级通道在线建模有源噪声控制算法
2018-06-25陈卫松崔婷玉仝喜峰
张 丽,陈卫松,崔婷玉,仝喜峰
(安徽师范大学 物理与电子信息学院,安徽 芜湖 241003)
有源噪声控制在治理低频噪声方面具有明显的优势,已经较成功地应用于封闭空间、管道、结构声辐射和声传输等方面的噪声控制[1]。有源噪声控制系统的关键技术除了噪声控制环节,还包括次级通道建模环节。次级通道依据系统建模的状态分为离线建模和在线建模两大类。离线建模是先对次级通道进行辨识然后进入主动噪声控制环节。该方法结构简单,易于硬件实现,但是不能及时地跟踪由于环境变化造成的次级通道参数的改变[2]。为了保证降噪算法的实时性、稳定性,通常对次级通道采用在线建模的方法。它能够对次级通路参数进行实时更新,当次级通道发生突变时能让系统快速恢复到稳定状态。基于在线建模的有源噪声控制系统中,次级通道建模精度直接影响到系统稳定性及收敛效果[3]。主动控制信号会严重影响次级通道建模精度,同样次级通道建模的建模信号也对主动控制有一定影响。提高次级通道建模精度、解决建模信号与主动控制信号的相互干扰是有源噪声控制需要考虑的关键问题。
Eriksson[4]首先用附加的随机白噪声作为建模信号,对次级通道进行在线建模,但建模信号与控制信号会相互干扰,严重时会导致系统不稳定、算法发散。Bao为了减少主动控制环节对建模环节的影响,在Eriksson算法中加入一个辅助自适应滤波器。Kuo采用一个误差预测滤波器,通过信号延迟将建模误差信号从期望信号中分离。Bao和Kuo的方法都是从期望信号着手来减少主动控制环节对建模环节的影响,但没有解决建模信号对主动控制信号的影响。张明等[5]在此基础上引入了第三个滤波器,通过抵消建模误差信号中的控制信号,有效解决了建模信号与主动控制信号间的相互影响。杨铁军等[6]在文献[5]的基础上增加了一个误差通道滤波器,在调整建模滤波器和第三个滤波器的误差信号中减去控制信号经过建模滤波器的滤波。这些算法思路都是通过增加自适应滤波器来改进算法控制性能,存在主动控制结构设计难度大、算法的计算量大和算法复杂度高的问题[7]。
Akhtar[8]提出的对次级通道采用变步长算法(VSS-LMS)受到较多关注,这种方法在不增加结构复杂度的情况下,改善了Eriksson算法中主动控制信号对建模环节的影响。但是Akhtar算法没有考虑建模信号对主动控制信号的影响。Davari[9]提出了一种对建模信号进行开关控制的策略,当系统达到稳定状态时停止次级通道建模,当检测到次级通道发生变化时,注入建模信号重新建模,但是环境变化门限值需要再次调节[3]。Shakeel Ahmed[10]提出了调节建模信号功率的方案,第1阶段,建模信号功率随着次级通道建模滤波器的误差信号的功率而变化,第二阶段,建模信号功率随着两个相邻次级通道建模滤波器误差信号的相关估计而变化,该算法提高了系统性能。但是该算法引入了MFXNLMS算法,不仅结构复杂,计算量也远高于Akhtar算法。
1 基于梯度下降的在线建模算法
本文在Akhtar算法的基础上提出一种基于梯度下降的次级通道在线建模有源噪声控制算法,改进算法结构如图1所示。
其中:P(n)、S(n)分别为初级通道和次级通道,d(n)是期望信号,e(n)为降噪系统的残余误差信号,噪声源X(n)经过建模滤波器(n)得到(n),作为主动控制环节的输入信号,白噪声信号v(n)是建模环节的输入信号。

图1 改进算法结构图
Akhtar提出的方法中,f(n)是更新主滤波器和建模滤波器的误差信号。在次级通道建模中,收敛因子随着e(n)和f(n)能量比的变化进行调整。初始阶段,系统处于最不稳定状态,μs(n)采用最小值μsmin,随着系统收敛,μs(n)值逐渐增加,调节公式为[8]
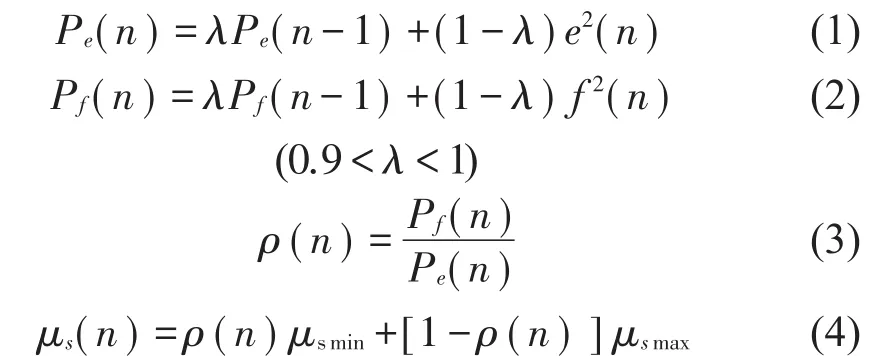
为改善Akhtar算法中建模信号对主动控制信号的影响,本文提出将μs(n)的调节方式与主动控制模块的收敛因子μw(n)的调节方式相结合,其中对建模收敛因子μs(n)进行梯度下降调整。
1.1 基于能量比ρ(n)的收敛因子调控
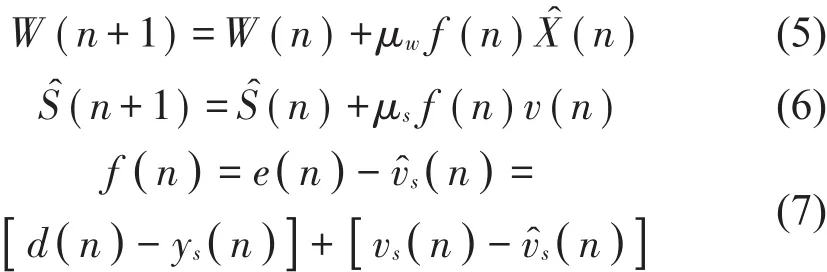
W(n)、(n)分别为主动控制环节和次级通道建模环节的自适应滤波器,根据各自环节的输入信号和误差信号及步长因子来自适应更新滤波器权值。式(5),式(6)[11]分别为自适应滤波器权系数的更新方式。式(7)[12]为更新建模滤波器(n)的误差信号,也是更新主滤波器W(n)的误差信号。白噪声信号v(n)和控制信号y(n)经过次级通道,输出[ys(n)-vs(n)]。在建模环节v(n)经过(n)输出s(n),如式(7)所示,误差信号f(n)中既包括建模环节的信号也包括降噪环节的信号,其中主动控制环节的理论误差[d(n)-ys(n)]会干扰(n)的更新,次级通道建模环节的理论误差[vs(n)-s(n)]也会干扰W(n)的更新,为了最大程度地减弱两个环节的相互影响,在线建模和主控制模块均采用变化步长值。
初始阶段控制模块的信号能量较高(此时ys(n),s(n)值 很 小 ,P[d(n)]>>P[vs(n)],即ρ(n)≈1),对建模系统影响较大,所以建模收敛因子μs采用小步长,而主动控制模块的μw采用较大步长值,随着系统逐渐收敛,[d(n)-ys(n)]逐渐变小,控制模块的信号能量逐渐降低(当迭代无数次(n→∞),[d(n)-ys(n)]→0),此时建模信号对主动控制模块的影响逐渐增大,所以μs逐渐变大,μw逐渐减小。主动控制模块μw更新方式为
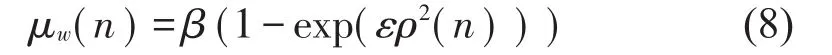
β,ε为固定参数,ρ(n)为本次运算所得能量值。在线建模模块μs更新方式为
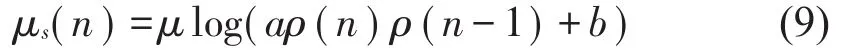
a,b,μ为固定参数,ρ(n)为本次运算所得能量值,ρ(n-1)为上次运算所得的能量值。从降噪速度和降噪量上与其他算法进行比较,得出其改进优势。
1.2 基于梯度下降方法的次级通道建模方法
上述收敛过程中,在线建模的步长值μs(n)由小到大变化,但是较大步长值会影响建模精度,并且干扰系统稳定性,严重时会导致系统发散。为了获得更好的建模精度和稳定性,后期对步长值采用梯度下降方法,本文利用建模精度的变化检测步长值是否进行下降。
函数C(n)为在线建模精度实时值,本文将C(n)作为μs是否进行下降的检测函数,同时设置T1、T2两个下降阈值。其中T1为步长仅采用μs(n)的建模中,ΔS刚开始收敛时刻C(n)的值;T2为第一次下降条件下,ΔS刚开始收敛时刻C(n)的值。
基于梯度下降的建模方法具体步骤:
(1)初始阶段,即检测函数C(n)大于T1时,建模收敛因子μs采用步长值μs(n);
(2)步骤(1)虽然提高了建模收敛速度,但是建模精度低,为保持原收敛速度的同时获得较好稳态误差,对μs进行第一次下降,即当T2<C(n)<T1时采用定步长μ1,为得到较好收敛效果,二者关系应满足max[μs(n)]-μ1<0.015;
(3)当C(n)<T2时,对μs进行第二次下降,μs采用定步长μ2()0.015< μ1-μ2<0.02 。所述C(n)的表达式为

M是建模滤波器长度,S(n)为次级通道脉冲响应(横向FIR滤波器),(n)为建模滤波器。从收敛性能和建模精度跟其他算法进行比较,得出其改进优势。
2 仿真结果分析
为验证本文改进算法的性能,在MATLAB中将张明的算法、Akhtar算法和本文改进算法进行仿真实验。为了精确衡量在线建模的收敛性及精度,定义次级通道建模误差为
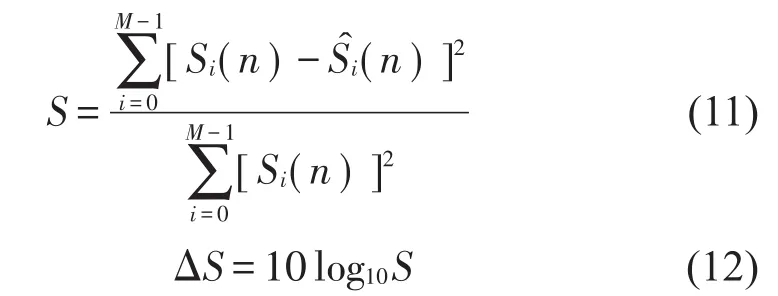
定义系统降噪量为
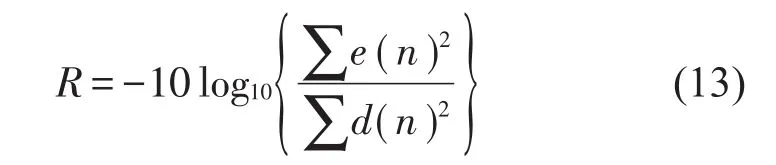
设置初级通道和次级通道的传递函数,主控制滤波器长度和建模滤波器长度分别为32和16,张明算法中第三个滤波器长度为16,仿真图均是在相同实验下取10次平均所得的结果。参数设置如表1所示。
初级通道P(n)的传递函数为
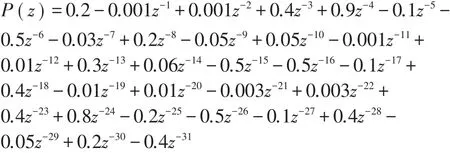
次级通道S(n)的传递函数为
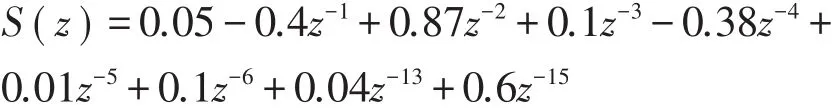

表1 算法参数设置[9]
2.1 混频信号降噪算法仿真分析
初级声源为50 Hz,150 Hz,300 Hz的单频信号组合后叠加白噪声信号,信噪比(SNR)为30 dB。取均值为零、方差为0.05的高斯白噪声作为次级通道辨识的建模信号。Akhtar算法与张明算法仿真参数分别按照文献[9]设置,经过多次实验分析,下降阈值 及 定 步 长 值 为 :T1=1×10-4,T2=2×10-5,μ1=2.5×10-2,μ2=5×10-3,λ=0.99,采 样 频 率为Fs=2 000Hz。
仿真结果如图2所示,图2(a)是控制模块收敛因子的变化,图2(b)是建模收敛因子的变化,初始阶段控制信号能量较高,控制模块选取较大步长值,因控制信号对建模环节影响较大,所以建模滤波器选择小步长值。
随着系统迭代,控制信号逐渐减小,主滤波器步长值从大到小变化,建模滤波器步长值则从小到大变化。系统迭代2000次后,建模滤波器步长进行第1次下降,迭代2500次后其进行第2次下降,可以获得较低的建模稳态误差。从图2(b)中可以看出,本文算法中建模滤波器步长值逐渐增大,后期步长逐级下降,初始阶段大于Akhtar算法的步长值,较大的步长可以有效提高建模误差的收敛速度,后期较小的步长可以获得较低的建模误差稳态值。图2(a)、图2(b)中收敛因子的调节方式能减小两个环节的相互影响,二者步长未同时出现较大值,系统能一直处于稳定状态。次级通道建模精度和系统降噪性能分别如图2(c)和图2(d)所示,由图2(c)可见,本文提出的算法较张明和Akhtar算法获得了较低的次级通道建模误差值,同时(n)快速收敛至S(n)。图2(d)中迭代5000次时本文提出算法已收敛,Akhtar算法与张明算法还未收敛,由图可见,本文算法在降噪量和降噪速度上都有所改进。本文算法增加了检测函数C(n)的计算同时μw由定步长换为变步长,与Akhtar算法相比,增加了计算量,因未加入第3个滤波器,计算量小于张明算法。
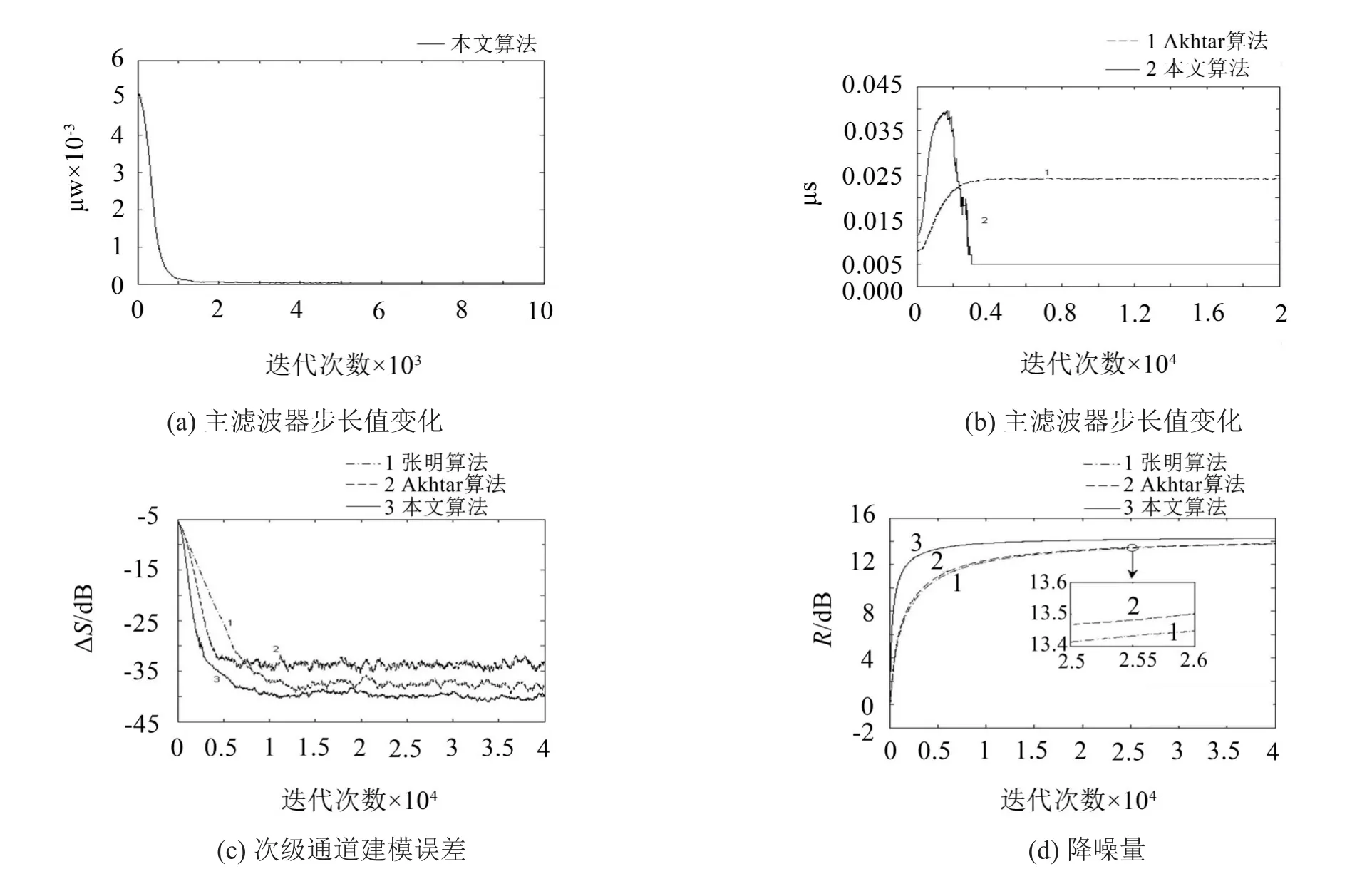
图2 混频噪声信号算法性能比较
2.2 次级通道时变的降噪算法仿真分析
实际情况下次级通道是随时间不断变化的,这就需要控制算法能够快速跟踪这种变化。假设系统迭代30000时通道发生突变,其他仿真条件和2.1节相同。
次级通道的传递函数为
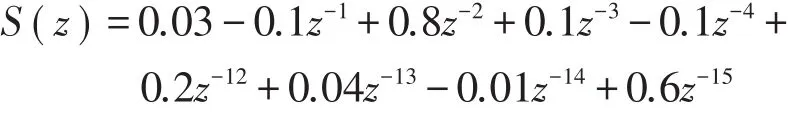
仿真结果如图3所示。图3(a)是控制模块收敛因子的变化,图3(b)是建模收敛因子的变化,图3(c)是次级通道建模误差的变化,图3(d)是系统降噪性能的变化。
可以看出,当次级通道在迭代30000次后发生突变条件时,本文改进算法通过自适应调整收敛因子使系统快速恢复到稳定状态。相较于其他两种算法,该算法在次级通道建模上依然保持高收敛率和低稳态误差值,从图3(d)可以看出,本文算法仍然保持较快收敛速度和较好的降噪量。
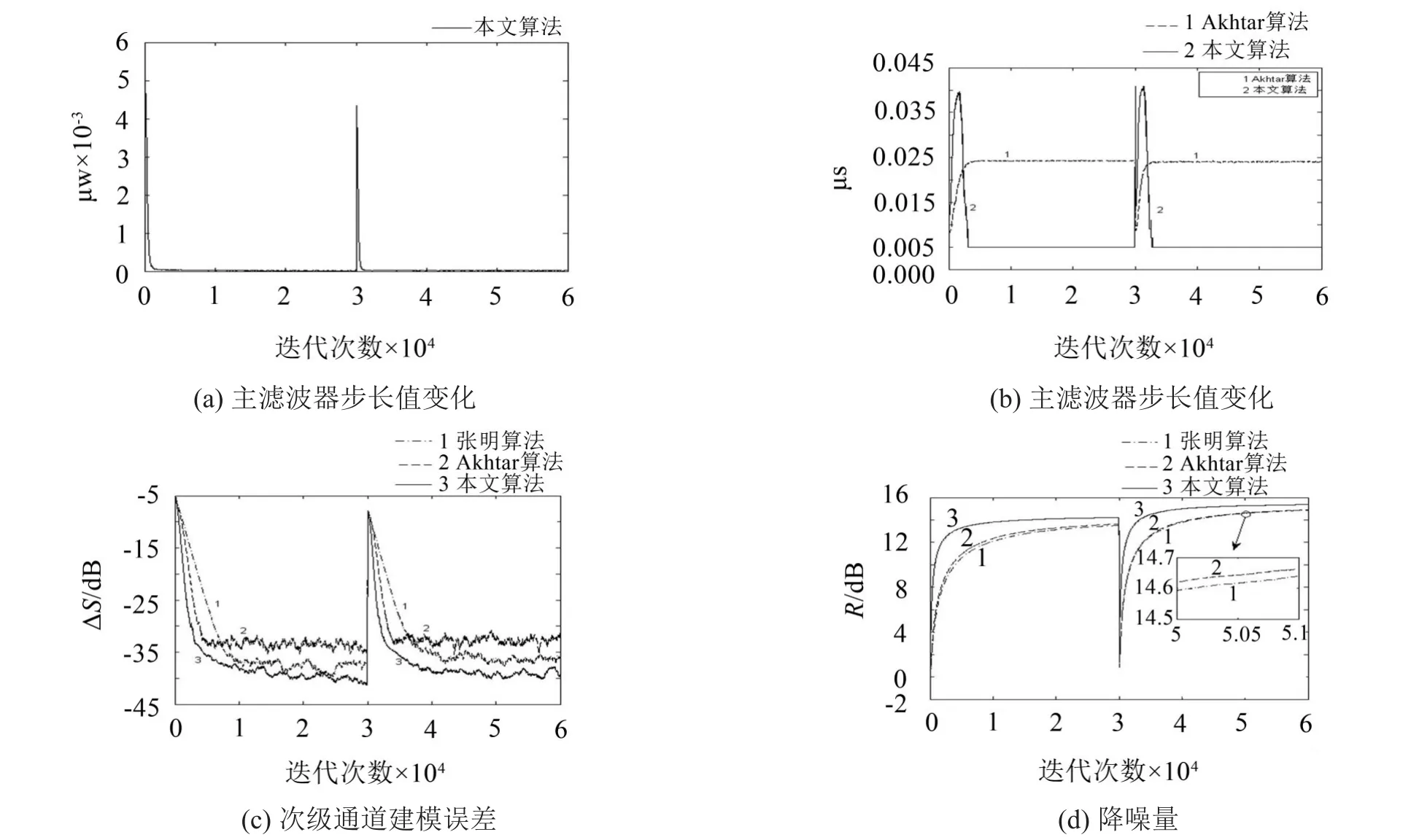
图3 次级通道时变的控制算法性能比较
3 结语
本文基于梯度下降方法,提出一种次级通道在线建模的有源噪声控制算法。针对在线建模有源噪声控制算法中建模信号对主动控制信号的影响及参数调整工作量大的问题,该算法将主动控制收敛因子调节方式与建模收敛因子调节方式相结合,并将梯度下降方法应用于在线建模中收敛因子的控制,仿真结果表明该算法具有收敛速度快,稳态误差低的特点,在次级通道发生时变的条件下仍然保持高收敛速度和低稳态误差值。本文算法涉及下降阈值参数较多,噪声源发生较大变化时阈值参数需要重新设定,后期需要在该方面进行进一步研究改进。因硬件调试结果不理想,下一步仍需在该方面进行研究。
[1]朱明刚,靳国永,肖友洪,等.声振主动控制系统中误差通道的在线辨识问题[J].噪声与振动控制,2005,25(4):18-22.
[2]孙金玮,孙琳,等.一种含次级通道在线辨识的窄带主动噪声控制系统[J].仪器仪表学报,2011,32(2):252-257.
[3]杨茜,吴超,付强,等.ANC次级通道在线建模的辅助噪声控制方法[J].网络新媒体技术,2014,3(5):43-46.
[4]ERIKSSON L J,ALLIE M A.Use of random noise for online transducer estimate in an adaptive attenuation system[J].Journal of the Acoustical Society of America,1989,85(2):797-802.
[5]ZHANG M,LAN H,SER W.Cross-updated active noise control system with online secondary path modeling[J].IEEE Transactions on Speech and Audio Processing.2001,9(5):598-602.
[6]杨铁军,顾仲权,鲁明月,等.基于次级通道在线辨识的结构振动主动控制系统[J].振动与冲击,2004,23(3):55-59.
[7]浦玉学,张方,姜金辉,等.基于次级通道在线辨识新算法的振动主动控制[J].振动、测试与诊断,2016,36(1):28-35.
[8]AKHTAR M T,ABE M,KAWAMAT M.Noise power scheduling in active noise control systems with online secondary path modeling[J].IEICE Electronics Express,2007,4(2):66-71.
[9]DAVARI P,HASSANPOUR H.Designing a new robust on-line secondary path modeling technique for feedforward active noise controlsystems[J].Signal Process,2009,89:1195-1204.
[10]AHMED S,AKHTAR M T,ZHANG XI.Robust auxiliarynoise-power scheduling in active noise control systems with online secondary path modeling[J].IEEE Trans on Audio,Speech,and Language Processing,2013,214(4):749-761.
[11]陈克安,马远良.自适应有源噪声控制—原理、算法及实现[M].西安:西北工业大学出版社,1993:133-138.
[12]ERIKSSON L J,ALLIE M A.Use of random noise for online transducer estimate in an adaptive attenuation system[J].Journal of the Acoustical Society of America,1989,85(2):797-802.
