防空导弹尾追拦截目标的遭遇点预测方法
2018-06-25朱梦杰
王 磊,朱梦杰
(上海机电工程研究所,上海 201109)
0 引言
防空导弹通常拦截迎击状态的目标,但随着防空任务需求的多样化,当导弹发射前后目标穿越发射点上空或发射期间目标远离发射点时,会形成导弹尾追拦截目标的情况。预测遭遇点参数在导弹发射条件判断、弹道设计及弹上飞控逻辑的实现中具有重要意义。快速、准确的预测遭遇点参数对充分发挥武器系统作战性能有着重要影响。影响遭遇点预测的因素很多,包括导引方法、目标运动特性、拦截态势等诸多方面。相比于迎击目标,尾追态势下目标初始参数装订值域扩大,导弹拦截过程存在迎击转尾追或全程尾追的情况,在此基础上的弹目运动几何关系和预测方法也会产生新的变化。根据目标初始装订信息,在兼顾迎击与尾追拦截态势的前提下,快速准确的预测弹目遭遇点成为一个值得研究的问题。
现有关遭遇点预测问题所提出的方法依据采用算法的不同可大致分为以下几类:一类是解析法,此类方法通常依据弹目相对运动关系或轨道特征参数,推导形成遭遇点预测的解析模型,能直接计算或通过迭代计算预测命中点[1-5],也可将遭遇点预测转化为一元高次方程的求解,从而简化问题的复杂度[6];一类是数值积分法,根据导引指令及弹体、目标运动学模型以及初始发射条件,解算运动学弹道至弹目遭遇,从而获得理论遭遇点位置[7];还有一类常用于弹道式飞行器的遭遇点预测修正方法,将弹目的动力学方程进行泰勒展开并舍去高阶项,以便形成离散形式的预测滤波模型,通过对目标数据序列滤波得到目标轨迹,从而计算得到预测遭遇点[8-9]。对比可知,解析算法求解过程一般采用对模型进行简化和近似处理的方法,多应用于目标弹道易于解析化表达的情况,因此不太适用于寻的制导方式的弹道,简化得到的近似解与真实遭遇点间存在偏差。数值积分法需要对气动、指令形成、弹目运动学等进行建模,计算过程即弹目运动方程的求解过程。该算法通常面临计算精度与计算效率之间的矛盾。预测修正方法基于对目标参数的预测滤波,滤波计算复杂,资源开销大,工程应用受到较大限制。
目前涉及遭遇点预测的研究中通常结合导引规律设计给出迎击条件下的预测算法,尚未涉及尾追目标态势下的遭遇点预测方法,同时解析法和数值积分法工程应用受限。因此本文考虑尾追拦截的弹目相对运动关系及工程应用对计算效率的需求,针对性解决了尾追态势的模型适用性和收敛性问题,采用数值方法建立了便于递推求解的遭遇点预测模型。首先根据弹目相对运动关系建立遭遇点预测模型,针对尾追态势分析了模型收敛性及适用性。然后结合尾追拦截态势及预测模型收敛条件,优化运动关系描述并设计了兼顾迎击、尾追目标的迭代算法。最后通过典型遭遇点对预测算法的收敛性和预测精度进行了仿真研究,验证了其有效性。
1 尾追拦截与遭遇点预测
在射击坐标系中,目标由初始位置以一定速度运动至遭遇点,导弹由发射点按照既定导引规律运动至遭遇点。发射、遭遇斜距及目标轨迹构成了拦截过程的弹目运动轨迹。导弹与目标的相对运动关系如图1所示。
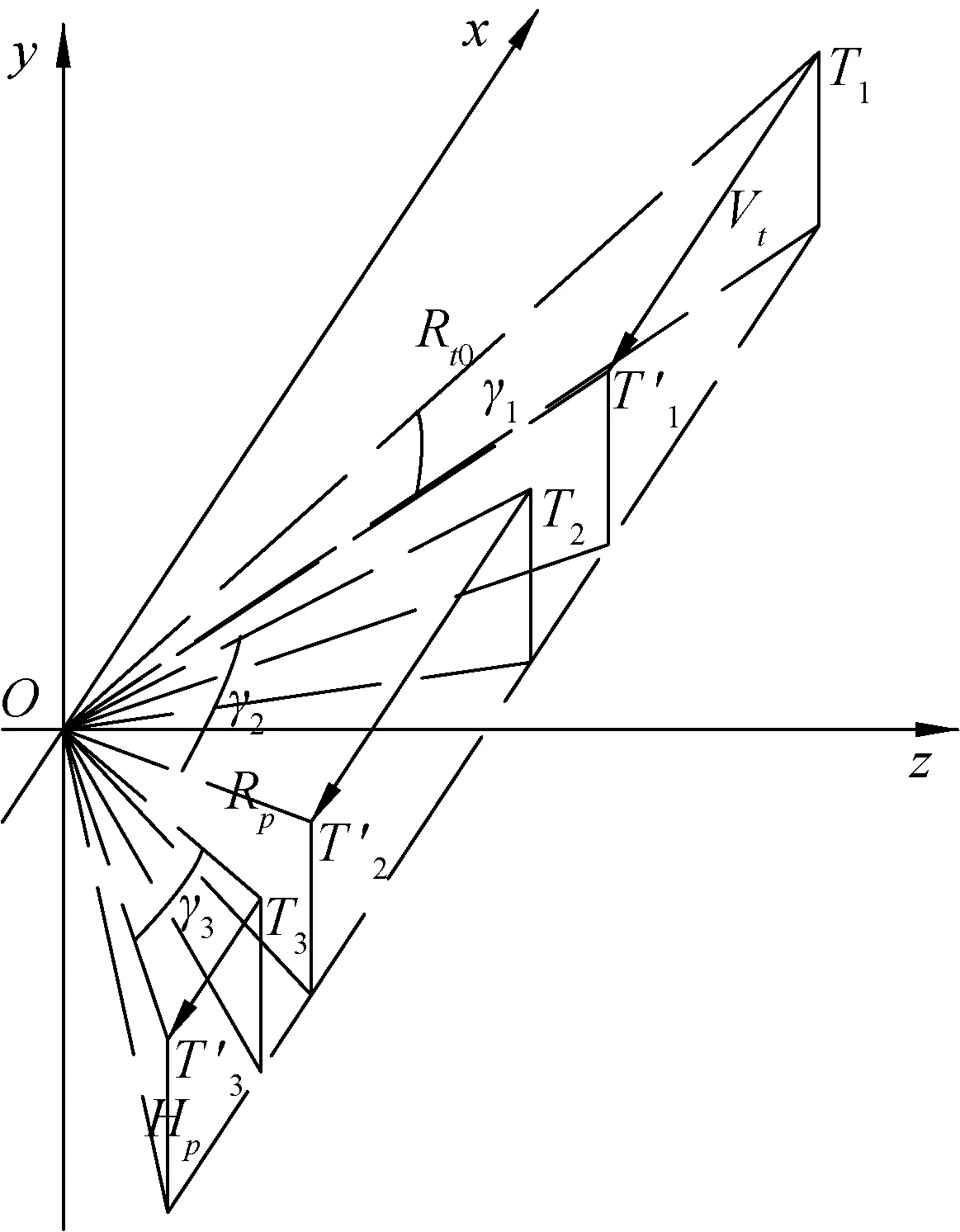
图1 弹目遭遇态势Fig.1 Missile-target encounter situation
导弹拦截目标时,武器系统决定目标是否具备拦截条件,并在满足发射条件时控制导弹发射,遭遇点参数Hp和Rp是决策、控制导弹发射过程的关键数据[10]。为判定发射窗口,遭遇参数需要在导弹发射前确定[11-12]。导弹发射后,Rp,Tp用于导弹初始转弯入射角计算,中、末制导参数调参以及武器系统的照射资源切换。遭遇点预测需要解决的问题,即发射前根据武器系统装订给导弹的目标初始参数,结合导弹速度特性及飞行情况,计算理论遭遇点高度Hp、斜距Rp及遭遇时间Tp。
2 遭遇点预测模型
2.1 模型建立
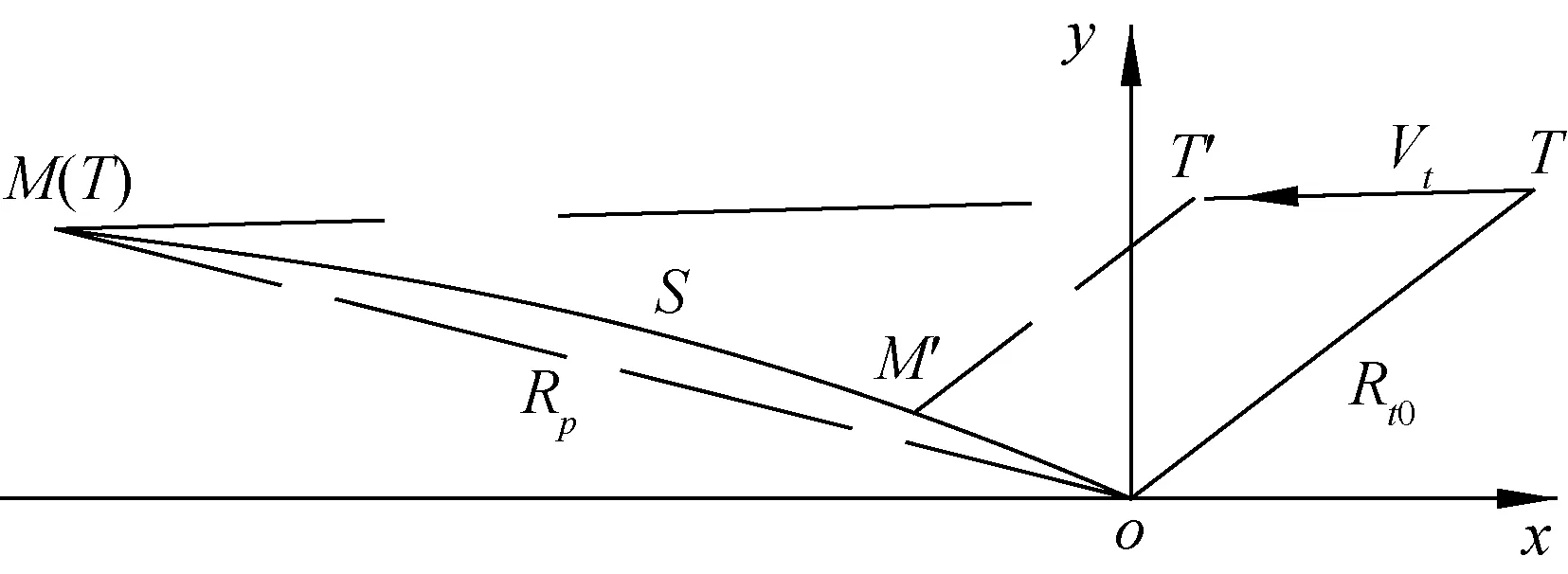
图2 弹目相对运动和预测遭遇点Fig.2 Missile-target relative movement and predicted impact point
根据图2,假定初始装订给导弹的目标位置信息为(xt,yt,zt),速度信息为(vxt,vyt,vzt),则目标初始斜距及其变化率计算如下
(1)
设导弹发射到遭遇时间Tp内发射点与目标连线扫过的角度为γ,目标初始斜距与目标轨迹之间的夹角为θ,几何关系为
(2)
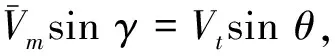
(3)
式中:Ω为初始视线旋转角速度,Ω=|Rt0×Vt|/Rt0。根据平行接近关系遭遇时间
(4)
(5)
由Tp计算Rp,得
(6)
将式(3)~(6)整理得到
(7)
(8)
2.2 预测算法分析
分析可知式(7)方程系数仅与目标初始装订值有关,若对式(7)采用迭代法进行求解,形如方程x=φ(x)的迭代收敛性有如下结论[14]。
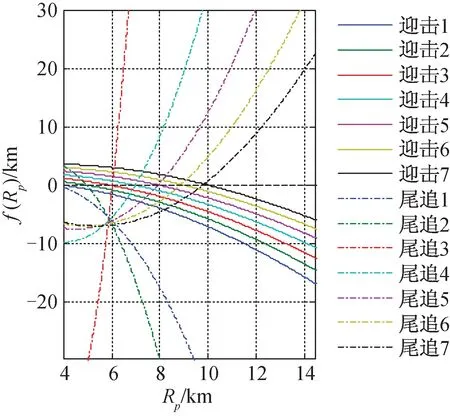
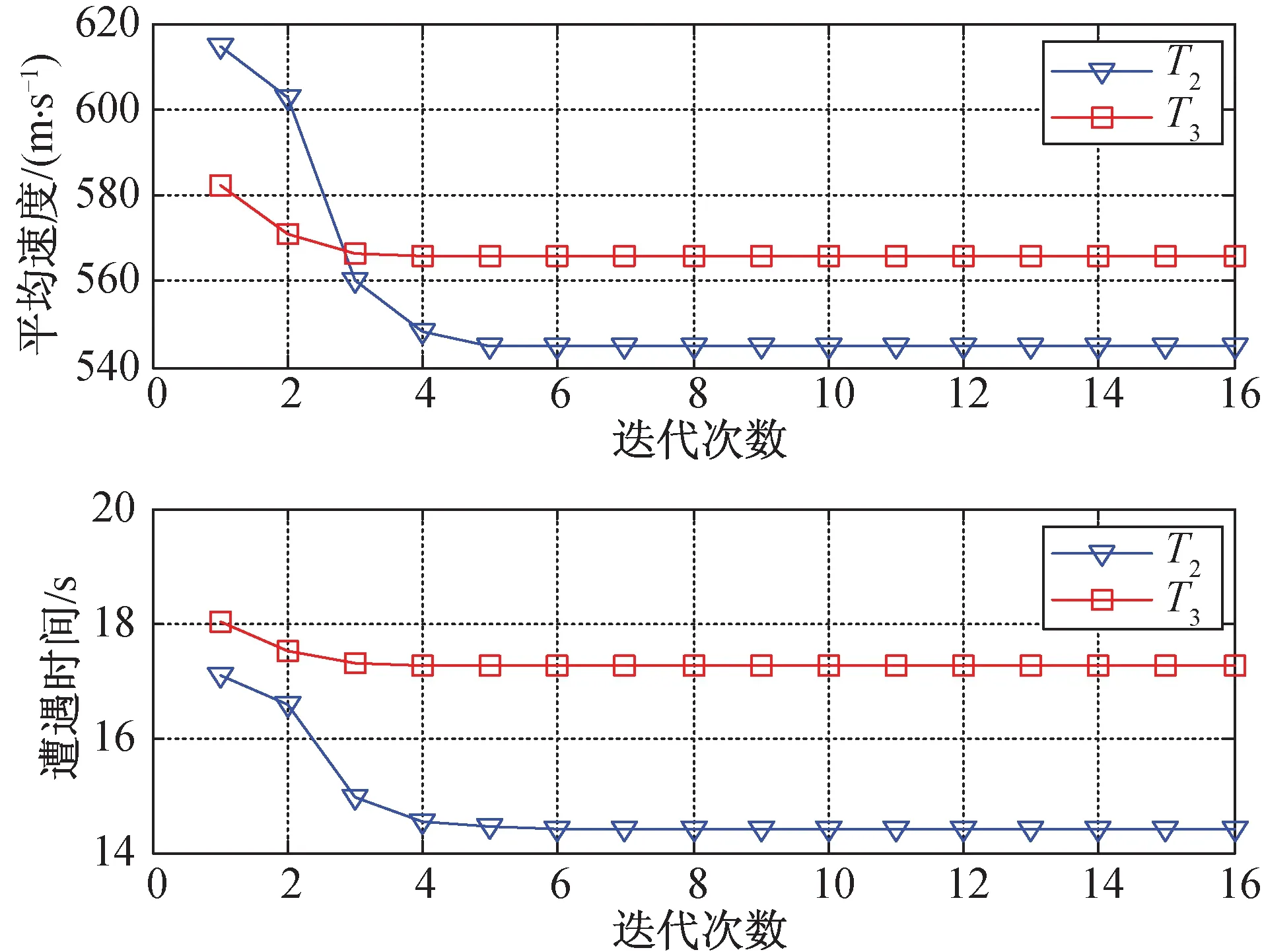
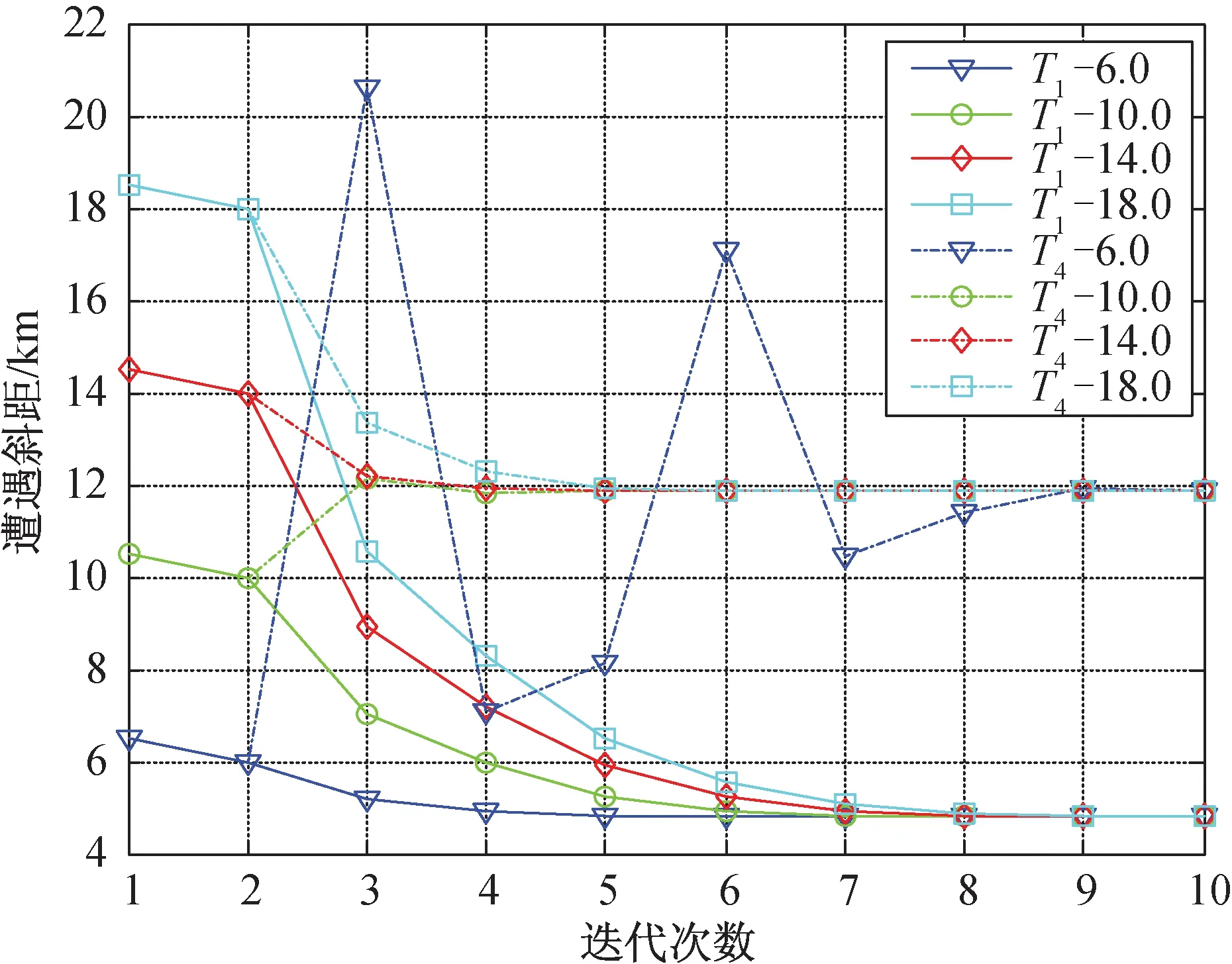
若迭代函数φ(x)在区间[a,b]上满足:1)x∈[a,b]⟹φ(x)∈[a,b];2)φ(x)满足∀x1,x2∈[a,b],有|φ(x1)-φ(x2)|≤L|x1-x2|,且0 在给定(xt,yt,zt)及(vxt,vyt,vzt)的条件下,式(7)的收敛性是确定的。迎击与背离目标的区别在于目标初始参数的差异,不同目标初始位置条件下迭代方程特性如图3所示。 图3 迭代方程特性Fig.3 Iterative function characteristic (9) (10) 针对式(7)模型收敛性与适用性所存在的问题,对预估模型进行优化。当γ>90°时,根据图2几何关系对模型修正为 (11) 将式(5)、式(6)代入式(11)并整理得 (12) 联立式(6)并代入式(4)可得 (13) 式(11)对应的γ值域为(0°,180°),故式(13)考虑了目标在低空尾追拦截时的适用性,能够描述T1,T2,T3各种拦截情况下的弹目运动。分析可知式(13)是关于Rp的一元高次方程,记式(13)右端为g1(Rp),对g1(Rp)求导可得 (14) 不同拦截态势下目标初值形成的函数g1(Rp)特性有较为明显的差异,将尾追近界点参数代入g1(Rp)出现g1(Rpmin) 将式(13)进行整理可得f(Rp)=0,函数f(Rp)表达式为 (15) 图4 尾追态势初值条件下的f(Rp)特性Fig.4 Characteristic of f(Rp) for tail- chase situation initialization 典型目标初值对应的f(Rp)曲线如图4所示。结合图4可知f(Rp)在导弹拦截范围内存在过零点,且该特性与目标的迎击或尾追态势无关,因此必定存在符合弹目运动关系的遭遇点。而f(Rp)=0求解算法应满足收敛条件宽松,收敛速度快两方面要求。根据数值计算相关方法,形如f(x)=0的方程,Newton迭代法求解的局部收敛性定理要求满足[15]: 1)f(x)=0存在单一根x*; 2)x*的邻域内f′(x)连续。 根据f(Rp)单调性及过零点的情况,宜采用Newton迭代法求解。为避免计算f(Rp)导数,离散化的递推形式为 (Rp(k)-Rp(k-1))(k=0,1,…) (16) 确定迭代初值需要考虑的因素包括收敛性和迭代次数。初值选择需要在可能的遭遇点附近,一方面满足局部收敛性条件,另一方面减少迭代次数。在导弹典型拦截范围内考虑全空域收敛速度,确定迭代初值 (17) 式中:Rpmax,Rpmin分别为杀伤斜距远,近界。ε为遭遇斜距迭代要求的收敛精度,ε<Δ。满足以下任一条件结束迭代:迭代次数大于n次; |Rp(k+1)-Rp(k)|<ε。其中迭代次数n和收敛精度ε根据计算效率及使用需求确定。 按式(17)确定Rp的迭代初值,根据目标装订位置(xt,yt,zt)和装订速度(vxt,vyt,vzt)计算迭代参数形成迭代公式。迭代过程按如下步骤进行: 2) 由式(15)计算f(Rp); 3) 由式(16)根据k与k-1步的Rp和f(Rp)计算Rp(k+1); 4) 由式(6)计算Tp; 5) 由式(8)更新Hp,Rp; 6) 判断终止条件,满足则结束,否则转步骤1)。 遭遇点预测模型解算流程如图5所示。 图5 预测模型解算流程Fig.5 Calculation process of forecast model 预测得到的遭遇点参数可用于发射条件判断、弹道设计及弹上飞控逻辑的实现。 以典型目标遭遇参数对应的发射点作为算例,分析预测模型设计的有效性。T1~T4均为速度500 m/s的超低空平飞目标,目标飞行高度0.1 km,理论遭遇斜距5.0~12.0 km,设置不同的航路捷径,射击坐标系下理论装订参数及遭遇参数见表1,迭代初值Rp(0)=10,Δ=0.5。 表1 典型目标态势 表2、表3为迭代计算结果,将优化前后的计算情况进行了对比。根据表中数据可知,优化前模型虽然较好地预测了迎击态势的遭遇点,但对尾追情况不适用,会出现迭代发散或预测至限幅值的情况。优化后模型则能同时适应迎击、尾追的拦截情况。 表2 迎击拦截斜距预测结果 表 3 尾追拦截斜距预测结果 从迭代次数可以看出,优化后的迎击平均迭代次数增加0.5步,尾追迭代次数平均增加1.25步,优化后迭代计算量与优化前相当,满足实际应用。图6中给出了优化后尾追迭代中平均速度与遭遇时间的收敛情况。 图6 迭代次数及收敛过程Fig.6 Iteration number and convergence process 通过预测值与实际仿真遭遇斜距的比较可知,对迎击目标遭遇斜距的预测误差不足1%,对尾追目标遭遇斜距预测相对误差约3%,预测精度完全满足发射条件及弹上逻辑的使用要求。 以T1,T4目标为例,不同迭代初值条件下尾追预测的收敛过程如图7所示。结果表明:在合理范围内的初值都能够较好的收敛,以式(17)确定的初值能快速收敛至理论遭遇斜距。优化模型并未限定目标的遭遇态势,该模型对各种目标态势均有较好的适应性。仿真计算表明:优化模型适用于全空域迎击、尾追目标的遭遇点预测。 图7 遭遇斜距收敛过程Fig.7 Encounter slant-range convergence process 遭遇点预测精度受目标测量及机动的影响,目标参数的装订误差会影响迭代精度,工程应用中需考虑雷达测量误差引起的参数摄动,统计可能出现的最大误差量级。应用中多数情况下可将目标视为非机动目标,但目标在突防、规避等特殊运动状态下,其机动的不确定性使遭遇点的预测变复杂。针对性分析目标可能的机动形式及时机,预测其机动规律以改善模型精度是需要进一步研究的工作。 对于防空导弹遭遇点预测问题,本文通过对目标拦截态势的分析,给出一种兼顾迎击的尾追态势下遭遇点参数预测方法。该方法通过分析弹目相对运动,在合理假设的基础上给出优化的弹目运动描述,以此为基础设计遭遇点预测迭代模型,使算法在预测遭遇参数时不受拦截态势的影响。仿真结果表明:预测算法对运动关系的优化改进是有效的。在可行域内,预测算法对迭代初值的选择无特殊要求;对不同点的验证表明,预测计算量小,算法平均迭代收敛次数少;相比常规遭遇点预测方法,给出了适用于尾追拦截态势的预测模型;考虑了不同遭遇点导弹速度特性的变化,预测精度高,便于工程应用。此外,目标信息的精度和运动特性会影响遭遇点预测准确度,后续可考虑机动情况下的目标速度预估完善迭代模型。同时,应进一步研究分析引入目标机动后的迭代收敛性。 [1] 张友安,马国欣,万宇. 一种弹目遭遇点预测方法[J]. 海军航空工程学院学报, 2011, 26(5): 513-516. [2] 李荣宁,刘敏. 中远程战术导弹预测命中点的计算[J]. 现代防御技术, 2001, 29(3): 23-26. [3] AHN J, ROH W R. Noniterative instantaneous impact point prediction algorithm for launch operations[J].Journal of Guidance, Control, and Dynamics, 2012, 35(2): 645-648. [4] 王君,周林,雷虎民. 地空导弹与空中目标遭遇点预测模型和算法. 系统仿真学报, 2009, 21(1): 80-83. [5] 李辕,赵继广,白国玉,等. 基于预测碰撞点的剩余飞行时间估计方法[J].北京航空航天大学学报, 2016, 42(8): 1667-1674. [6] 余名哲,张友安,钱进. 基于遭遇点预测的比例导引与多平台接力制导交接律设计[J]. 海军航空工程学院学报, 2010, 25(3): 255-259. [7] 张华伟,董茜,王文灿,等. 基于预测命中点的反弹道导弹拦截方法研究[J]. 弹箭与制导学报, 2007, 27(2): 196-199. [8] YUAN T, BAR-SHALOM Y, WILLETT P, et al. Impact point prediction for thrusting projectiles in the presence of wind [J]. Signal Processing, Sensor Fusion, and Target Recognition XXI, 2012. [9] ZHANG X, LEI H M, LI J, et al.Ballistic missile trajectory prediction and the solution algorithms for impact point prediction[C]// Navigation and Control Conference. Yantai, China: Proceedings of 2014 IEEE Chinese Guidance, 2014: 8-10. [10] 高方君. 空袭目标威胁评估模型研究[J]. 上海航天, 2005, 22(2): 11-14. [11] 陈怀瑾,吴北生,梁晋才. 防空导弹武器系统总体设计和试验[M]. 北京:宇航出版社, 2002: 117-119. [12] 于本水,杨存富,张百忍. 防空导弹总体设计[M]. 北京:中国宇航出版社, 1995. [13] 李 翼,钟生新,陆永红. 防空导弹平均速度分析[J]. 火力与指挥控制, 2004, 29(6): 88-93. [14] 李信真. 计算方法[M]. 西安:西北工业大学出版社, 2000: 18-23. [15] 韩旭里. 数值分析[M]. 北京:高等教育出版社, 2011: 36-40.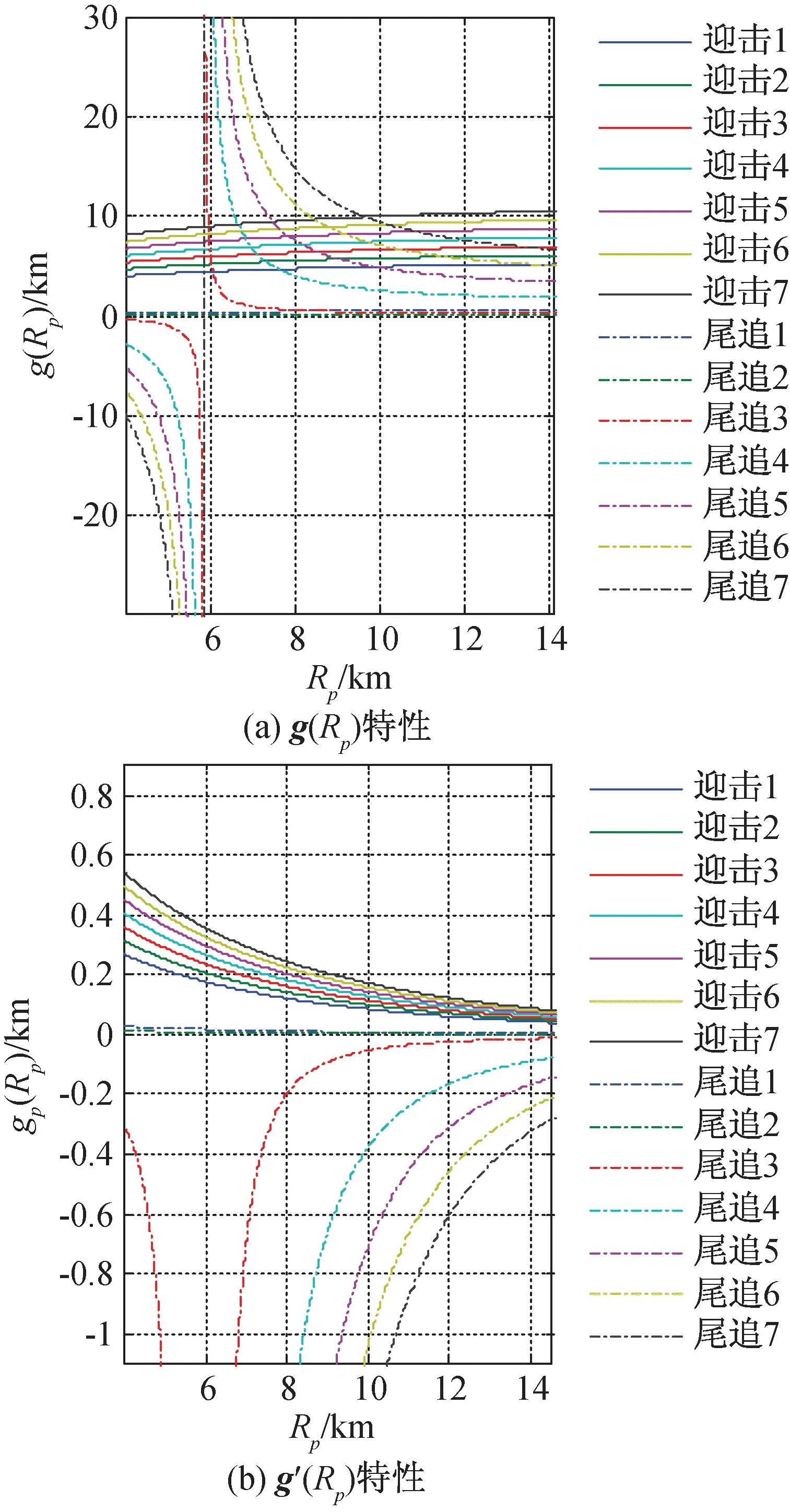
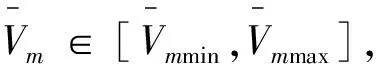
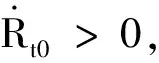
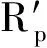
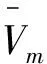
2.3 尾追拦截模型优化
3 遭遇点预测模型解算
3.1 迭代算法
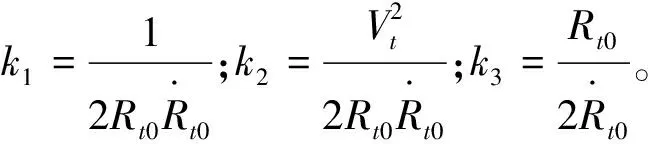
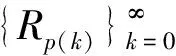
3.2 初值及终止条件
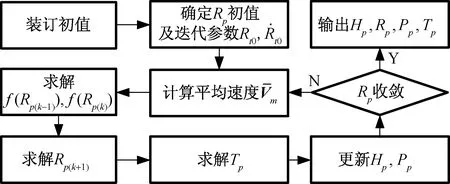
3.3 预测模型解算流程
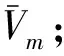
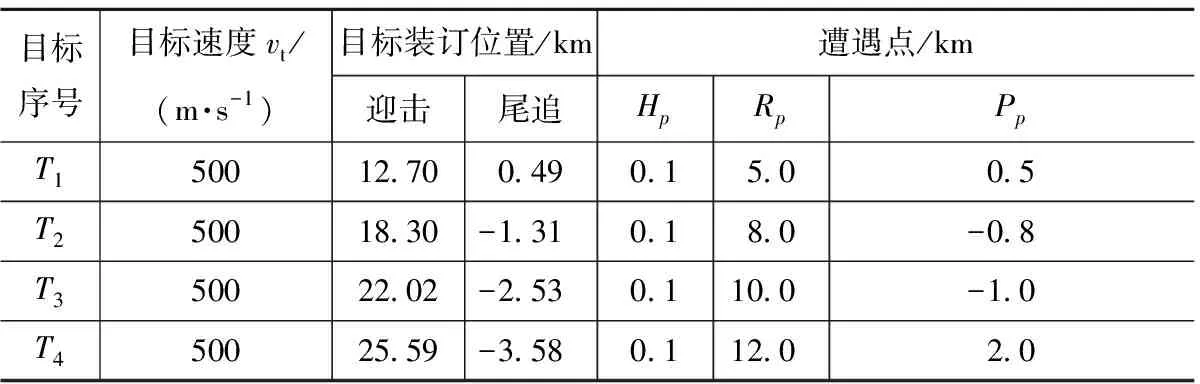
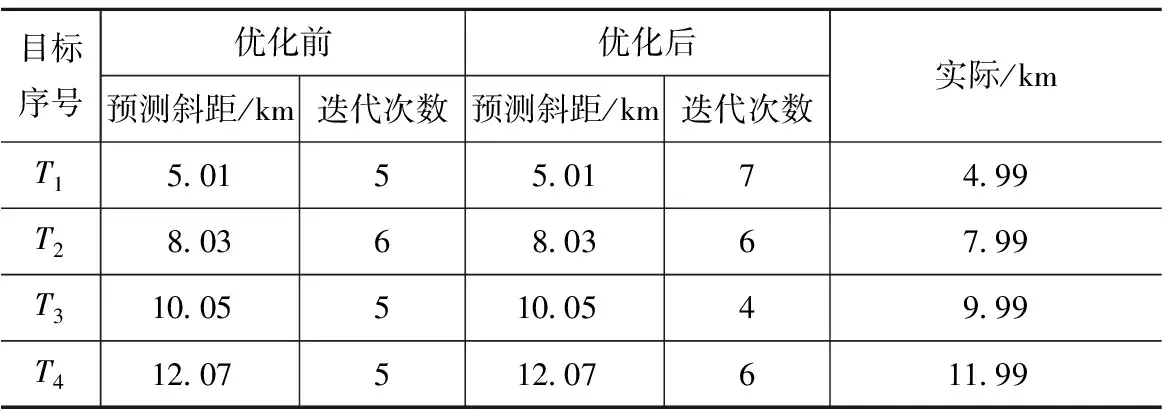
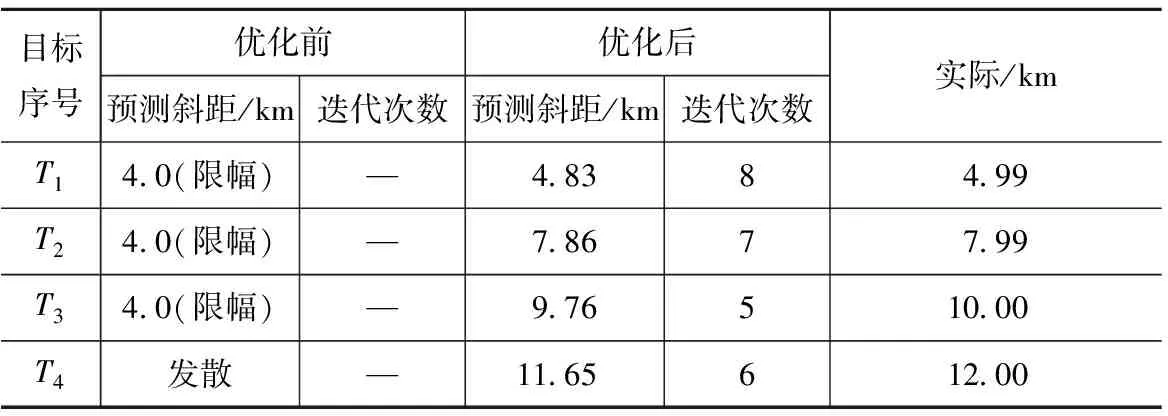
4 仿真结果
5 结束语
