开放世界下的雷达辐射源融合识别算法研究

2018-06-25谢春禾郑翰清

上海航天 2018年3期

谢春禾，蒋雯，刘翔，郑翰清

(1. 西北工业大学电子信息学院，陕西西安 710072； 2. 上海航天控制技术研究所，上海 200233；3. 中国航天科技集团公司红外探测技术研发中心，上海 200233)

0 引言

雷达辐射源识别是一种重要的电子对抗技术，它通过将侦察到的雷达信号特征参数和雷达库中已知雷达的特征参数进行对比，以确定待测雷达的类型，并进一步分析该雷达的用途、载体、威胁等级等。雷达辐射源识别的工作原理为：如果待测雷达的各特征参数与数据库中某雷达相应的特征出现高度一致时，则认为待测信号的雷达属于该类别。

虽然雷达辐射源的工作原理很简单，但在实际应用中，准确识别雷达型号是一件艰难的任务，原因主要为以下三点：一是雷达对抗系统探测的各参数可能存在误差；二是雷达特性参数不是固定值，会在一定范围内波动；三是不同雷达的特征参数时常相同或相近，而现代战场电磁环境复杂多变，敌对双方通常会采用各种反侦查的措施，从而增加了雷达辐射源信号的复杂性、欺骗性、模糊性，使侦察设备难以对雷达特征参数进行真实、可靠的探测。以上原因催生了许多关于雷达辐射源识别算法的研究。如：关欣等[1]提出了一种基于模糊综合评判的雷达辐射源识别新算法，该算法通过构造模糊评判矩阵表示辐射源相关程度的模糊集，然后按最大隶属度原则进行判决；刘凯等[2]研究了一种脉间特征参数和脉内特征参数隶属度的计算方法，提出了一种综合特征权值的算法，对雷达辐射源进行加权识别；黄高明等[3]提出了一种基于高速DSP(数字信号处理器)芯片的神经网络硬件实现方法；何隆玲等[4]提出了基于自适应时变权重和局部搜索算子的改进PSO(粒子群优化算法)，并结合RBF(径向基函数神经网络)进行了雷达目标识别；张政超等[5]研究了一种基于粗糙集数据处理的雷达辐射源识别模型；王虹等[6]研究了一种基于面积计算灰关联度的改进方法，并将其成功应用于辐射源识别。

近年来，基于信息融合技术的方法受到越来越多的关注，该方法能缩短侦查系统的探测时间，扩大系统的探测范围，具有很强的势态感知和威胁评估能力，被广泛应用于目标识别等领域。其中，D-S证据理论是一种有效的不确定推理工具，能对目标的不确定信息进行有效建模和分析，并通过融合目标的多属性信息进行有效的推理和决策。目前，D-S证据理论在雷达辐射源识别上有许多研究，并取得了一定成效。如：俞至富等[7]提出了基于灰关联分析与D-S证据理论的多传感器雷达辐射源识别方法，提高了辐射源识别率；黄小毛等[8]提出了基于D-S证据理论与模糊理论组合应用的方法，充分利用了雷达信号在时间上的冗余信息，提高了信号的识别率。D-S证据理论是建立在闭合世界下的，即假设研究范围内不存在未知目标。实际上，随着雷达反侦察技术的发展，想要充分获取敌方雷达信息并非易事，因此难以建立一个完备的雷达库。在这种情况下，当侦测到新型雷达信号时，传感器数据可能无法与现有雷达匹配，导致误判。因此，D-S证据理论在雷达辐射源识别中的作用具有一定的局限性。

针对上述问题，本文基于广义证据理论[9-11]研究了一种在开放世界下的雷达辐射源融合识别方法。对未知类型雷达的识别进行了研究和建模，将雷达参数模糊化处理，引入广义证据理论，构建广义的概率指派函数，在开放世界下进行证据组合和决策，并验证该方法的有效性。

1 理论基础

D-S证据理论[12-13]是由Dempster提出并由Shafer改进的一种信息处理方法，被广泛应用于不确定信息的表达和处理。该理论首先构建了一个辨识框架Θ={θ1,θ2,…,θN}，Θ由N个互斥的元素组成的集合，其中每个元素对应1个判别的命题，因此辨识框架为所有判别命题的集合；然后，在辨识框架下建立了BPA(基本概率指派函数)，该函数为1种信任程度，用来表示辨识框架中任意子集命题的信度大小；最后，提供了Dempster组合规则，即

(1)

式中：集合A，B，C为辨识框架中除空集外的任意子集，且A为B，C的交集；k为冲突因子。该规则可在没有先验信息的情况下实现证据融合。

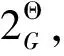
(2)

则m为框架Θ上的广义基本概率指派。与BPA相比，GBPA没有m(∅)=0的限制，即m(∅)不必强制为0。空集表示不属于辨识框架中的命题，因此，可将空集的信度用于判别新目标。广义证据组合规则(GCR)为

(3)

式中：m为GBPA；K为2组GBPA之间的冲突程度；m(∅)为空集的信度赋值。

式(3)中，空集的信度不要求为0，且参与和其他焦元(focal element，信度大于0的命题)的融合运算。通过融合后空集的信度大小判断待测目标是否为未知目标。但在研究中发现，当证据数目较多时，式(3)中的空集信度随乘积运算进程愈来愈小，最终向0收敛。为解决该问题，JIANG和ZHAN在广义D-S证据理论[10]基础上提出了1种修正的广义证据组合规则(MGCR)[14]，公式为

(4)

式中：集合A，B，C为辨识框架中除空集外的任意子集，且A为B，C的交集。

与GCR[10]相比，MGCR优化了空集信度的融合方式，将空集作为1个正常焦元进行归一化处理，避免了空集信度越融合越小的问题。因此，后文将采用式(4)进行证据融合。

2 雷达辐射源融合识别模型

2.1 设计思路

雷达信号包含工作频率、脉冲重复频率、脉冲宽度、频率捷联方式、重频参差方式、信号调制方式、使用高度等参数信息。这些参数隐藏着雷达辐射源的信息，对空中目标识别具有重要价值。当待测雷达信号完成变换、滤波、特征提取等处理后，可得到针对不同参数的特征值，利用这些特征值可产生相应的BPA，从而通过信息融合技术实现目标的综合判别。特征提取为生成BPA的重要环节，若信息特征提取不准确，则可能导致生成的BPA不可靠，最终使融合结果不可信。

由于雷达信号可能受环境噪声及敌方人为干扰的影响，探测的信号具有一定的模糊性和不确定性，最终提取到的特征值具有一定偏差。因此，雷达参数库中样本的特征参数也具有一定模糊性，有必要将不同类型(单值型、多值型、区间型)的雷达参数进行模糊化处理，建立雷达样本的模糊隶属度模型。在实际环境中，捕捉到目标平台雷达信号的时间可能有限，在短时间内可能无法充分获取完整的测量参数，因此对于多值型或区间型的雷达参数，可先采用实时的单值型数据匹配样本模糊隶属度产生GBPA，利用修正的广义D-S证据理论组合规则融合多组特征参数的信息，得到综合的识别结果。若有参数更新，则进行后续的融合识别。为识别雷达辐射源，本文按照这种思路，提出了1种基于广义D-S证据理论的信息融合模型，如图1所示。

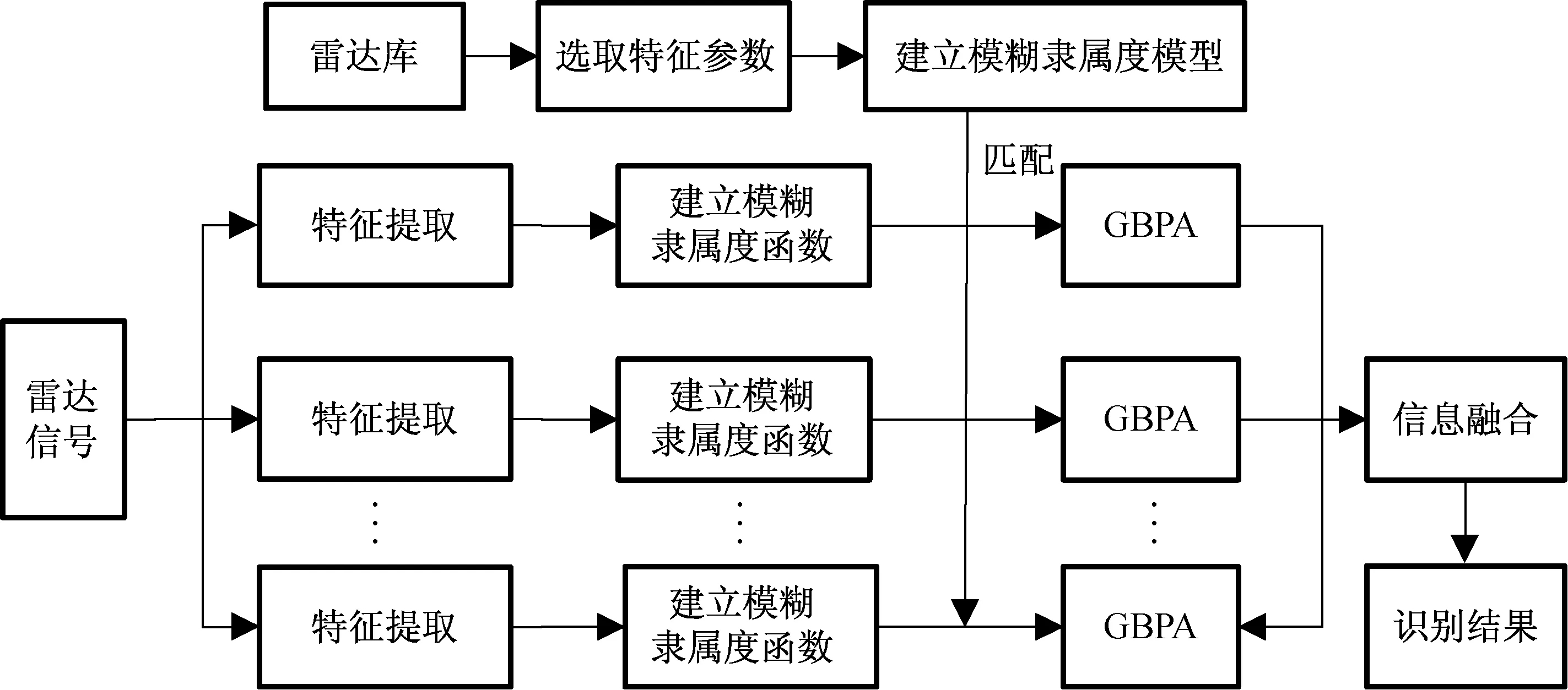
图1 开放世界下雷达辐射源融合识别模型Fig.1 Fusion model of radar emitter recognition in open world

2.2 建立雷达库雷达参数的模糊隶属度函数

雷达的参数变量类型有差异，实际侦查的雷达信号提取的特征参数有单值型、多值型和区间型。如KOHTYP雷达的工作频率为9 435 MHz，该频率为单值型雷达参数；P6∏-4雷达的脉冲宽度为0.4，1，2 μs，该脉冲宽度为多值型的雷达参数；Buran-D雷达的脉冲重复频率为250～1 500 Hz，该脉冲重复频率为区间型雷达参数。因此，在模糊化雷达参数变量时，需根据不同的参数类型定义不同的模糊隶属度函数，特别是针对多值型、区间型参数需定义完整的隶属度函数，有些学者在模糊化多值型参数时仅考虑其中的某一个值(如最大值)的做法缺乏合理性，容易导致信息的缺失。下面以3种不同类型的雷达参数为例，说明本文采用的特征参数模糊化方法。

假设雷达库有t种雷达，Θ={U1,U2,…,Ut}，每种雷达Ui(i=1，2，…，t)具有n种特征参数用于待测雷达的辐射源识别，则某样本雷达Ui(i=1，2，…，t)的第j种特征参数εj的模糊隶属度函数为μij(x)。针对不同参数类型定义不同的隶属度函数。

1) 单值型。对于单值型雷达参数，采用正态型模糊隶属度函数进行模糊化，如图2所示。隶属度函数表达式为

(5)

式中：Xij，δij分别为接收机雷达对参数j测量的均值和标准差。

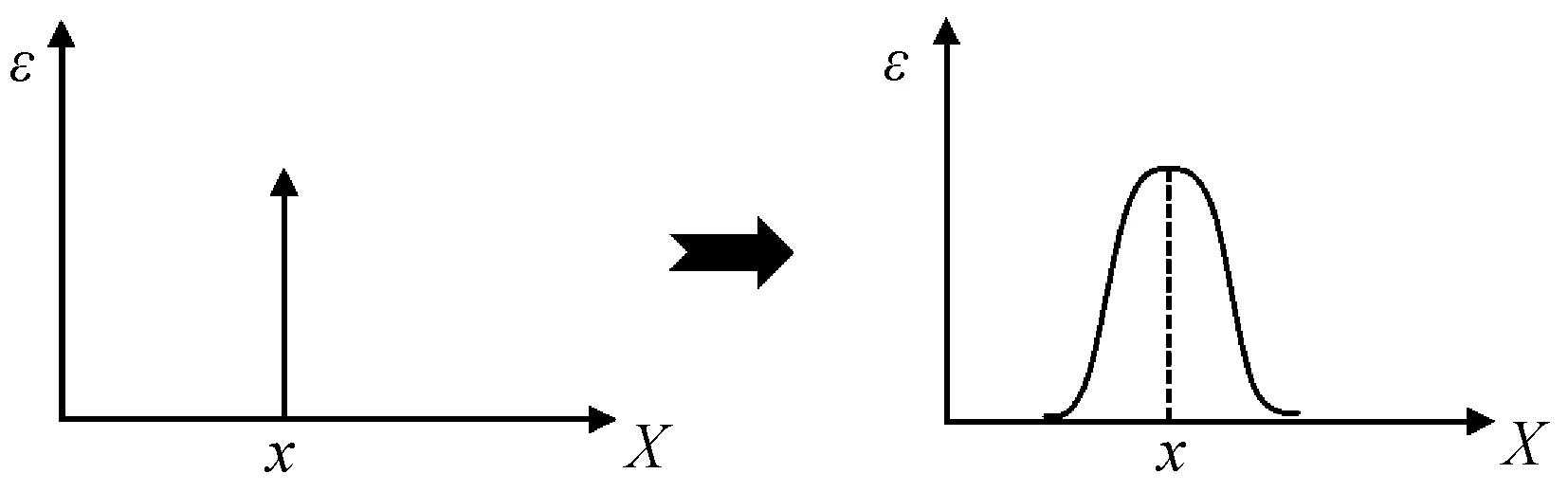
图2 单值型雷达参数的模糊化Fig.2 Fuzzification of radar parameters with single value

2) 多值型。对于多值型雷达参数，要对每个参数进行模糊化处理。由于雷达某参数可能是其中的一个值，也可能在几个值之间切换，所以只模糊化参数的一个值或部分值都会造成信息损失，导致目标识别的效果不佳。因此，在对多值型参数进行模糊化时，要构造每一种可能取值的隶属度函数，如图3所示。

图3 多值型雷达参数的模糊化Fig.3 Fuzzification of radar parameters with multiple values

假设某雷达的某参数有N个可能取值，则根据式(5)可得该参数第n个取值的模糊隶属度模型，为

(6)

式中，n为1，2，…，N。

多值型参数的隶属度函数为

(7)

式(7)表示将N个参数都进行模糊化处理。

3) 区间型。区间型雷达参数的模糊化过程如图4所示。

图4 区间型雷达参数的模糊化Fig.4 Fuzzification of radar parameters with interval value

假设某区间型雷达参数的取值为Xmin～Xmax，则定义的模糊隶属度函数为

μij(x)=

(8)

2.3 目标命题的GBPA的生成方法

假设待测雷达T在特征参数εj下的模糊隶属度函数为μTj(x)，则其λ截集的定义为

(9)

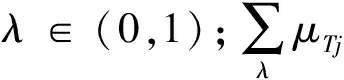
在λ截集函数下，通过分析待测雷达各参数隶属度函数与样本雷达模板的似然度来确定目标命题的GBPA，具体方法如下。

定义待测模糊隶属度函数μTj(x)与样本雷达μij(x)的似然度为2个模糊隶属度函数的最大交点，公式为

(10)

测试参数与单值型或区间型样本匹配的似然度可直接利用式(10)求得。对于多值型样本参数，将待测样本在某参数下的λ截集函数分别与多值型参数的每一个可能取值的模糊数相匹配，并取最大值，匹配的似然度定义为测试参数与模型的匹配值，是一种可能性大小，公式为

(11)

(12)

即当似然度之和不超过1时，将剩余值赋给空集。

(13)

即当似然度之和超过1时，将似然度归一化后作为GBPA，空集的信度为0。在多属性信息融合中，雷达的每个特征参数相当于一类多源信息。对于n种特征参数，通过式(9)～(13)可相应产生n组GBPA。

2.4 GBPA的融合方法及决策准则

经典的D-S证据理论存在冲突悖论问题，即Dempster组合规则在融合高冲突的证据时可能会产生不合理结果。同类问题也存在于广义D-S证据理论中。为防止在证据组合时发生这类问题，本文采用加权平均算法[15-16]实现冲突管理，公式为

(14)

式中:wj为第j个特征参数的权重。

由于不同特征参数对于目标识别的重要性不同，每种特征参数会有1个相对权重。通过加权平均，可得到一组平均证据，将式(4)融合n-1次，从而得到最终决策的GBPA。

基于以上融合结果，定义以下决策准则：如果m(∅)>ρ1，则判别目标为未知目标；如果max(m(Ui))>ρ2，则判别目标为Ui。

由以上判别条件可知：当融合结果的GBPA中空集的信度超过阈值ρ1时，则将待识别目标判定为未知；当融合结果的GBPA中Ui的信度最大且大于阈值ρ2时，则判定待识别目标为Ui。

3 仿真及结果分析

采用工作频率、脉冲重复频率、脉冲宽度这3个雷达特征参数来识别雷达辐射源类型。从雷达库中选取3组已知型号的雷达(U1～U3)作为识别样本，其特征参数见表1。

表1 待测雷达与模板雷达的参数值

假设地面侦测设备检测6组待测雷达的信号为T1～T6，且由统计得知，该侦测雷达统计以上参数的均方误差分别为1%，1.5%和2%，则实验中，待测型号T1～T3为已知型号雷达，T4～T6为新型雷达。本文基于融合算法的待测雷达的识别步骤如下。

利用表1中的已知雷达参数建立模糊隶属度函数，将测试雷达的参数模糊化处理，同模型进行匹配产生似然度。图5为根据3个雷达特征参数下的测试雷达(T1)和目标库雷达的匹配模型。根据式(9)～(13)产生用于3个特征参数的3条GBPA。最后，通过式(4)的MGCR融合GBPA，并利用定义的判别规则对6个待测雷达进行判别。

为检验本文提出的雷达辐射源识别方法对新目标判别的有效性，分别将该方法与经典的D-S证据理论和广义D-S证据理论下的GCR方法进行比较，待测雷达的匹配结果见表2～5。表中加粗部分为1条BPA的最大信度值。在闭合世界下，BPA可采用式(12)、(13)生成，不同的是将公式中的空集替换为全集。融合后的决策方法与本文中的决策准则相同。

在闭合世界下，使用经典的D-S证据理论对雷达辐射源进行判别，结果见表2。由表2可知：T1～T3中仅有T2可判别；在T1和T3中，BPA的最大信度都没有超过阈值，因此产生的BPA无法对目标进行判别；在T4～T6中，T4和T5的BPA将最大信度分配给了全集，表示识别结果可能是目标库中的某一种，因此并不能将目标识别为未知；T6被错误识别为已知目标U3。

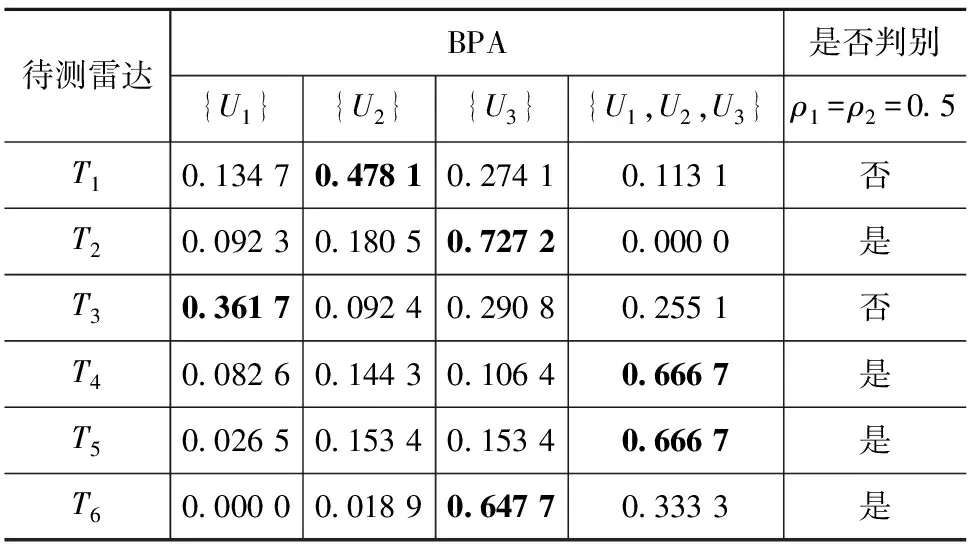
表2 闭合世界下的待测雷达的仿真结果

表3 在开放世界下基于GCR的待测雷达的仿真结果

在开放世界下使用GCR对雷达辐射源进行判别，结果见表3。融合后的T1的GBPA对未知型号的支持度仅为0.001 4，远低于门限值ρ1，所以认为待测雷达不是新目标。由于对目标库中雷达U2的支持度最高，且大于门限值ρ2，因此认为待测雷达T1为已知雷达型号U2。同样，目标T2和T3分别识别为U3和U1。对于新目标T4～T6，判别结果不容乐观，从T4和T5的融合结果可见，最大信度均不超过判决门限，因此无法判决。即使降低门限值，使最大信度可用于决策，由于空集的信度在融合时越来越小，最终也会将目标T4和T5判别为已知目标。因为空集的信度在融合时越来越小，所以T6最终被错误判别为已知目标U3。

图5 待测雷达T1与目标库雷达的匹配模型Fig.5 Matching model of radar T1 to be tested and radar in database

使用MGCR算法的雷达辐射源判别结果见表4，表中加粗部分为错误判别。由表4可知：T1～T3的判别结果和基于GCR的方法完全相同；按照决策准则，T4和T5判别为未知目标，与先验信息符合；T6被误判为已知型号U3。

表4 开放世界下基于MGCR的待测雷达的仿真结果

使用以上3种方法后的雷达辐射源识别结果见表5。由表可见：D-S证据理论的融合算法对于已知目标的判别具有较大的不确定性；在未知目标判定上，经典D-S证据理论失效，甚至得出了错误的判别结果；GCR方法对未知目标的判别也存在很大的不确定性。而整体上，基于MGCR的融合模型使目标的判别能力都有了较大的提升。因此，本文提出的辐射源识别模型具有更高的可靠性和更强的未知目标判别能力。此外，3种方法对T6均识别错误。经分析发现，该结果是由于T6的脉冲重复频率、脉冲宽度和已知型号U3对应的参数相同或相似导致的。即使工作频率这一特性和U3完全不匹配，融合后的证据依然有很大的信度支持目标U3。因此，本文提出的方法仅适用于不同雷达的特征参数存在一定区分度的场景中，即不同雷达的同类特征参数具有一定的差异性。如果不同雷达之间的特征参数相同或高度相似，则需建立更精准的雷达目标库，减少不确定性；增加信号峰值功率、辐射源使用高度等可用的雷达特征参数。

表5 开放世界和闭合世界下的目标识别结果比较

4 结束语

在开放世界下辨识框架并不完备，存在着未知目标，因此，在开放世界下研究目标识别具有重大意义。本文提出了1种基于广义D-S证据理论的雷达辐射源识别模型，将目标识别引入开放世界进行讨论，用空集的信度作为目标未知的证据。若目标已知，则空集的信度始终比较低。在辨识框架不完备时，若有新目标出现，则融合后的证据中空集的信度较大。通过对雷达辐射源的识别进行实验验证，验证了该方法具有较好的对已知目标识别和未知目标判别的能力。本文提出的GBPA生成模型还存在以下不足：一是雷达库中模板雷达的参数可能具有较大的重叠性，这就会对目标识别造成一定干扰；二是不同属性在信息融合中的权重可能不同，对于雷达辐射源识别，不同雷达类型在某一属性下重叠程度不同，属性交叉区域越大，则对目标区分的能力越弱，因而该属性的重要性就越小。因此，在后续工作中可基于属性间的交叉程度研究不同属性在融合中的权重系数。

[1] 关欣, 何友, 衣晓. 一种新的雷达辐射源识别算法[J]. 宇航学报, 2005, 26(5): 612-615.

[2] 刘凯, 白京路, 王春波，等. 一种基于模糊隶属度的雷达辐射源识别新方法[J]. 航天电子对抗, 2014, 30(5): 31-35.

[3] 黄高明, 苏国庆, 张琪,等. 基于神经网络的雷达辐射源智能识别系统[J]. 雷达科学与技术, 2005, 3(2): 86-90.

[4] 何隆玲, 胡桂明, 李维维,等. 基于PSO-RBF神经网络的雷达目标识别[J]. 现代防御技术, 2014, 42(5): 115-120.

[5] 张政超, 关欣, 何友. 粗糙集在雷达辐射源识别中的应用[J]. 中国电子科学研究院学报, 2009, 4(4): 412-416.

[6] 王虹, 关欣, 逯程. 基于面积灰关联算法的机载平台雷达辐射源识别方法[J]. 中国电子科学研究院学报, 2015, 10(5): 523-526.

[7] 俞志富, 罗景青. 基于灰关联分析与D-S证据理论的多传感器雷达辐射源识别方法[J]. 电讯技术, 2004, 44(1): 52-56.

[8] 黄小毛, 郑孝勇, 章新华. 基于D-S推理的雷达信号模糊识别方法[J]. 现代雷达, 2002, 24(4): 7-9.

[9] DENG Y. Generalized evidence theory[J]. Applied Intelligence, 2015, 43(3): 530-543.

[10] 邓勇,蒋雯,韩德强. 广义证据理论的基本框架[J]. 西安交通大学学报, 2010, 12: 119-124.

[11] 邓勇,韩德强. 广义证据理论中的基本概率指派生成方法[J]. 西安交通大学学报, 2011, 45(2): 34-38.

[12] DEMPSTERA P. Upper and lower probabilities induced by a multi-valued mapping[J]. Annals of Mathematical Statistics, 1967, 38(2): 325-339.