同类跟进：“较难题”教学的有效方式

☉江苏省张家港市港区初级中学 朱菊萍

每次期中考试、期末考试或模考之后，一线教师常常有这样的感慨：某道题碰到过多次，我们也讲过多次，但是能顺利解答的学生还是不多，至少没有达到我们理解的人数.原因固然是很复杂的，比如，学生听讲时感觉听懂，并一定会做，当时会做了但没有深刻理解问题的深层结构，过了一段时间，又忘了.为了提高学生对一些“较难题”（往往是一份试卷上承载着区分功能的把关题）的掌握，老师们有很多积极的教学举措.比如，我们注意到，如果能在一些较难习题讲评前，做好同类题的搜集，并在讲评一道较难题之后，再做同类跟进讲评或训练，往往就能收到较好的教学效果.这方面的经验在《中学数学》（初中版）近年也有多篇文章中提到（如文1～4），受到启发，本文也梳理近期教学过程中收集到的一些同类跟进式的习题讲评素材，整理出来提供分享，并跟进教学思考，提供研讨.

一、同类跟进讲评的题组案例

题组1：动点轨迹在一直线上

例1如图1，在等边△ABC中，D是线段AB上任意一点（不与A、B重合），将线段CD绕点C逆时针旋转60°得到线段CE，连接DE、BE.记BC中点为G，若AB＝2，补全图形并分析GE长度的最小值.

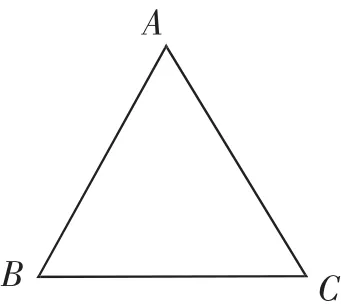
图1

思路简述：解题关键是发现点E在一条线段上运动（证△ACD≌△BCE，可得∠CBE=60°），于是过点G作GH⊥BE，垂线段GH的长即为GE的最小值.

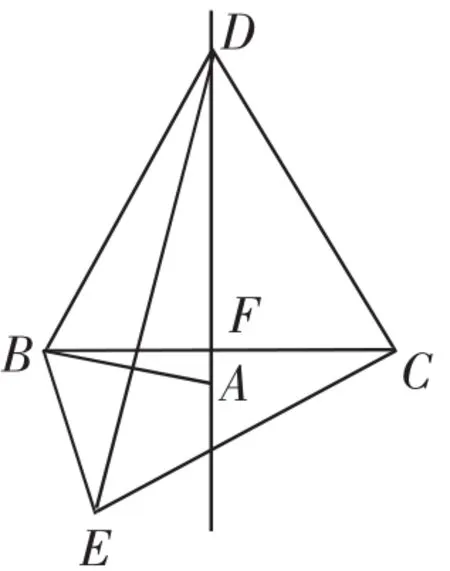
例2如图2，在等边△BCD中，DF⊥BC于点F，A为直线DF上一动点，以点B为旋转中心，把BA顺时针方向旋转60°至BE，连接EC.判断EC与DC的位置关系，并说明理由.

思路简述：先证△BCE≌△BDA，可得∠BCE=30°，于是∠ECD=30°+60°=90°，即CE⊥DC.将点A变换到FD延长线上时，仍然有上述性质：可确认E点运动轨迹是过C点垂直于CD的直线.认识到上述结构之后，还可提出如下问题：当∠DEC＝45°时，连接AC，求∠BAC的度数.（这里就需要考虑两种可能的情况，∠BAC的度数分别为30°或150°）

例3如图3，已知直线l：y＝kx＋b经过点A（0，4）和B（4，－4），C是x轴上的一个动点.将点B绕着点C顺时针旋转90°得到点D.小杰经过探究发现：点D在直线y=x上.请判断小杰的发现是否正确，并说明理由.

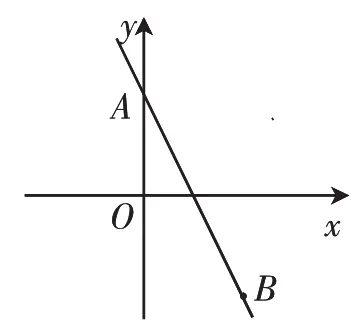
图3

图4

思路简述：由于点C作为旋转中心位置不定，可设点C的坐标为（m，0），如图4，过点B，D分别作BM⊥x轴，DN⊥x轴，垂足为M，N.先证出△MBC≌△NCD.ON＝m－4，DN＝m－4.点D的坐标为（m－4，m－4）.即动点D所形成的函数图像为直线y＝x.故小杰的发现是正确的.

题组2：“光线反射”最小值的变式问题

例4如图5，已知点A（3，4），B（－1，1），在x轴上另取两点E，F，且EF=1.线段EF在x轴上平移，当四边形ABEF的周长最小时，求点E的坐标.

思路简述：当四边形ABEF的周长最小，也就是AF+BE最小时，这时需要将其中一个点A或B左右平移EF的距离，比如将点A向左平移1个单位（EF的长）到点A′，再作点B关于x轴的对称点B′，连接A′B′交x轴于点E，于是点E即为所求.

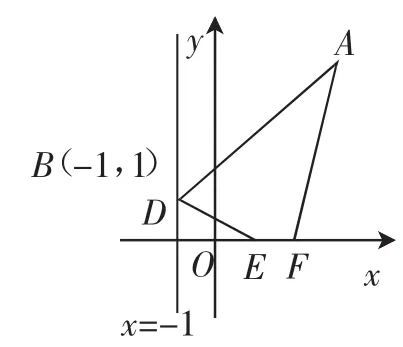
图5

图6

例4同类变式：如图6，在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，OA=3，OB=4，D为边OB的中点.若E、F为边OA上的两个动点，且EF=2，当四边形CDEF的周长最小时，求点E、F的坐标.

例5如图7，在平面直角坐标系xOy中，A是直线上一动点，将点A向右平移1个单位得到点B，已知点C（1，0），分析OB+CB的最小值.

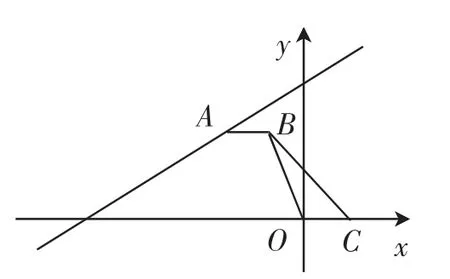
图7

思路简述：与例4及变式不同，这里虽然也是平移，但却是所谓的“镜面”平移，就是过点B作直线BD//直线，交x轴于点D.这里可过点C作直线BD的对称点C′，连接OC′，交直线BD于B点，则此时的B点为所求.接下来利用特殊直角三角形边角关系求出OC′的长为

二、进一步的思考

1.教师需要关注新题好题，及时归类并收藏相同结构问题

作为新时期教师专业成长的现实需要，我们应该重视一些优秀试卷、试题的收集与研习，除关注本地区的经典好题以外，我们还要进一步关注其他地区的各类好题，比如，值得关注的一些地区（如北京、上海、南通、南京等地）的期中、期末、中考考卷都应该在第一时间从网上获取，然后独立深处，归类收藏相同结构的问题，这样在习题讲评遇到同类问题时，就可以从自己的“资料库”中及时提取相关问题.这样来看，一个教师在短时间内能找出同类问题绝不是一朝一夕的功夫，而是长期的日积月累的归类收藏的苦功夫.

2.习题讲评课要聚集主题，较难习题讲评后跟进同类再练

我们看到很多的习题讲评课就题讲题现象比较普遍，往往一些较难题讲评之后学生貌似听懂，实则多数学生是伪懂，他们只是得到了答案，对问题的结构并不一定具有深刻的理解.我们常常发现一些学生听懂后并不一定会做，而会做了不一定能讲.所以作为较难习题的讲评建议，安排学生把思路再讲解一遍是较为有效的检查方式.另外，还需要在讲评后，及时跟进同类再练，以便加深学生对这类问题深层结构的理解.

3.较难习题讲评后易遗忘，两周内进行变式改编巩固效果

针对较难习题讲评之后容易遗忘的现象，我们可以在两周内对所讲较难习题在不改变原题深层结构的基础上，对试题的数据、字母、图形位置进行一些变式改编，安排时间检查学生对这些试题的巩固效果.比如，针对题组1，两周后可以挑选如下一道同类问题进行变式再练，巩固效果.

变式改编巩固题：如图8，已知点A（0，1），B是x轴正半轴上的一动点，以AB为边作等腰Rt△ABC，使点C在第一象限，∠BAC=90°.设点B的横坐标为x，点C的纵坐标为y，分析y与x的函数关系式.

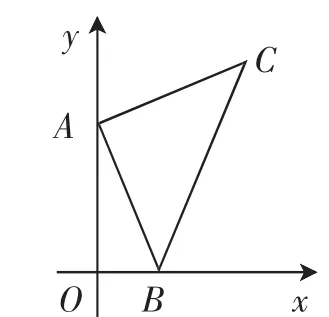
图8

三、写在后面

习题讲评是数学教师一项重要的专业能力，就题讲题是最低层次，追求一题多解可拓宽学生对问题解法的认识，是不少老师善于开展的解题教学追求；而由一题链接到其他同类问题则需要教师课前深入备课，而且要有长期的同类问题的归类收藏与积累，非一日之功，也可看成是成熟教师与初任教师或经验教师的一个区别所在，希望我们都能在“同类跟进”这一专业能力上不断精进.因此，我们要将习题讲评由就题讲题延伸到一题多解、一题多变、一题多法上来，真正达成举一反三的效果，以此发散学生的思维、提升学生的能力.又将习题讲评的课堂总结还给学生，启发学生在总结提升的过程中学会化整归一，真正以不变的方法与思想应对千变万化的题目和应用.

1.沈丽婧.聚焦微专题：中考二轮复习的实践与思考——以一组“关联试题”复习为例［J］.中学数学（下），2017（3）.

2.储秀梅.同类跟进：试卷讲评课的一种策略——以一道反比例函数把关题讲评为例［J］.中学数学（下），2017（5）.

3.俞丁立.解题教学，在难点处请勿“一带而过”［J］.中学数学（下），2017（9）.

4.朱建民，陈雷.关联同类微专题，铺垫设问助突破——以中考微专题复习为例［J］.中学数学（下），2018（2）.H