探寻问题本质，变式学习探究——以一道函数综合题为例

☉苏州高新区实验初级中学 杨 颖

中考函数压轴题以综合题居多，图像涉及众多函数，求解时需要深入探寻问题本质，采用适当的方法，对问题的条件进行转化，然后利用基本性质来求解.本文将详细讲解一道中考函数综合题的解题思路，并对其进行解读变式，开展教学思考，以供读者交流学习.

一、考题呈现及思路突破

1.考题呈现

题目（2016年江苏泰州中考数学卷第24题）如图1所示，反比例函数上存在A、B两点，坐标分别为A（m，4），B（－4，n），现经过点A、B作一直线，与x轴相交于点C，与y轴相交于点D，试求下列问题：

（1）如果m=2，求n的具体值；

（2）试求m+n的值；

（3）现连接OA、OB，如果tan∠AOD+tan∠BOC=1，求直线AB的函数解析式.

2.思路突破

分析：（1）m=2，则点A（2，4），反比例函数只有一个未知数k，只需一个点即可确定具体的函数解析式，点B位于反比例函数上，则其坐标必然满足反比例函数解析式，可以将其点坐标代入求解；（2）求m+n的值，需要先确定m和n的具体关系，又知m和n分别是点A和B的横坐标和纵坐标，则可以将点的坐标代入反比例函数解析式，从而分别获得m和n与反比例函数k的关系式，即4m=k，－4n=k，消去k，恒等变形后即可得到m+n的值；（3）tan∠AOD+tan∠BOC=1，求直线AB的解析式，对于角的正切关系，需要将其放在具体的直角三角形中，先作AE⊥y轴，垂足为点E，再作BF⊥x轴，垂足为点F，如图2，则则条件转化为，其中，则，结合第（2）问m+n的值，解方程即可分别确定m和n，则A和B的坐标均可求得，利用两点即可求直线AB的函数解析式.

图1

图2

解：（1）当m=2时，得A（2，4），代入，可得k=8，则反比例函数解析式为，把点B（－4，n）代入，解得n=－2.

（2）点A和B均位于反比例函数曲线上，将其坐标A（m，4）和B（－4，n）分别代入解析式（k＞0），可得4m=k，－4n=k，即4m=－4n，整理得m+n=0.

（3）作AE⊥y轴，垂足为点E，再作BF⊥x轴，垂足为点F，在Rt△AEO中，tan，在Rt△BFO中，.因为tan∠AOD+tan∠BOC=1，则.又知m+n=0，解得m=2，n=－2，则点A和B的坐标分别为A（2，4）、B（－4，－2），则直线AB的斜率为1，利用点斜式，可得y－4=x－2，整理可得直线AB的函数解析式为y=x+2.

二、考题解读及变式训练

1.考题解读

（1）考题的本质探索.

上述考题考查了两种函数图像，即反比例函数y=k x和一次函数y=kABx+b，以及三角函数，只不过将一次函数以两点连线的形式给出，另外，问题中涉及了三角函数tanθ（θ代表不同的角）.分析反比例函数解析式及曲线上的点，需要认识其本质，对反比例函数解析式进行变形xy=k，由于k为常数，则曲线上的点必然满足横、纵坐标的乘积为一恒定的常数，即对于点A（x1，y1）、B（x2，y2）、C（x3，y3）、…，必然有x1y1=x2y2=x3y3=…=k，因此对于求反比例函数解析式或其上点的坐标，可以采用“（x1，y1）→确定解析式点（x2，y2）”的模式.而分析一次函数解析式离不开对点坐标的求解，由于解析式y=k′x+b中最多含有两个未知数，因此其解析式的确定最多需要求得图像上的两个点.初中阶段的三角函数都是放在直角三角形中来研究的，因此对于问题中的三角函数，需要在图像中构建直角三角形，将其转化为相关线段的比值，利用线段的长度比值来建立方程求解.对于含有多种曲线的函数题，其实质上就是对图像的点、线、面之间关系的分析，最终还是需要结合函数解析式将其转化为研究点坐标的问题.

（2）考题的难点分析.

上述题目涉及了三个问题，第（1）问是相对基础的问题，只需借助“点坐标1→解析式→点坐标2”的模式即可完成.第（2）问求m+n的值，学生很容易陷入求解m和n的误区，由于反比例函数的解析式不能确定，因此含有m和n的点坐标无法求得，解题的难点就在于建立关于m和n的参数关系，通过消去参数的方式来直接获得m+n的值.本题目的一个特殊点在于点A的纵坐标与点B的横坐标互为相反数，基于反比例函数k的几何意义可得x1y1=x2y2=k，则必然有A的横坐标与点B的纵坐标互为相反数，即m+n=0，该特点既体现在具体的数值上，也体现在图像上，即A、B两点关于原点O呈现中心对称分布，这是该小问认识的难点所在.对于第（3）小问，其难点在于对含有三角函数条件的转化，初中阶段需要将其放在直角三角形中来研究，如何构建较为简洁的直角三角形成为解题的关键.如上述解题过程分别作了点A和点B到y轴、x轴的垂线，构建了Rt△AEO和Rt△BFO，则很容易将其线段的比值与点的横、纵坐标联系起来，如若构建的直角三角形不合理，则相关线段长度就难以表示，会导致解题的失败.因此在解题时不仅需要理解相关概念，还需要掌握相应的解题技巧，尤其是对于几何题的辅助线添加需要细致斟酌，确保解题思维的顺畅.

2.变式训练

对于考题的第（2）问和第（3）问，可以进行相应的变式，在不改变问题主旨的前提下加深学生对知识的理解，进一步拓展学生的解题思维，现对问题进行如下变式：

变式：如图3所示，反比例函数上存在A（m，4），B（－2，n）两点，现经过点A、B作一直线，与x轴相交于点C，与y轴相交于点D，试再次分析相似问题：

（1）如果m=2，求n的具体值；

（2）试求2m+n的值；

（3）现连接OA、OB，设直线AB的解析式为y=k′x+b，如果tan∠AOD+tan∠BOC=1，请直接写出不等式k′x+b≥的解集.

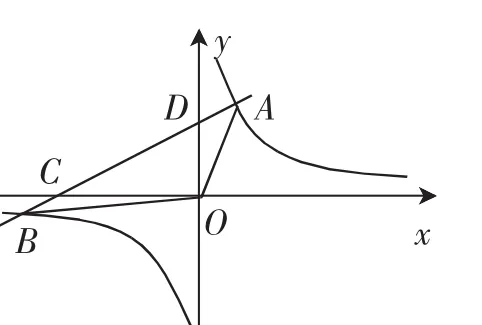
图3

变式思考：第（1）问的解题模式依然不变，解得n=－4；第（2）问发生了变化，但基于反比例函数k的几何意义获得的关系式x1y1=x2y2=k，依然可以建立m和n的关系，4m=－2n，整理变形可得2m+n=0；第（3）问求不等式k′x+的解集，分析不等号两边，左边为直线AB上点的纵坐标值yAB，右边为反比例函数上点的纵坐标值y1，则问题转化为x取何值时，yAB≥y1，图像上的直观体现则是直线AB的图像位于反比例函数图像的上方的x范围.初步观察可知为xB≤x＜0或x≥xA，则问题转化为求点A和点B的横坐标，衔接原考题求点A、B的坐标即可.

三、解后反思及教学思考

1.归类图像曲线，探寻考题本质

中考曲线压轴题的考查类型是多样的，涉及的函数图像也较为众多，如果仅仅将其看作多条曲线的简单集合是不利于分析的，也无法获得较好的解题策略.学习时需要对函数图像进行系统归类，对图像本质进行深入探究，明晰曲线结构，理解函数解析式，掌握函数相关问题的求解方向，然后将多函数图像进行归类整合，从函数图像的点、线、面之间的联系入手，总结相应的解题方向和解题策略.教学中有必要将函数图像设计成教学专题，引导学生对不同类型的图像问题进行解法归纳，加深学生对图像本质的理解，从而形成较为系统的解题策略.

2.注重分析方法，掌握解题思路

初中函数内容不仅需要掌握函数的解析式和图像性质，还需要将两者结合起来进行对应理解，这是函数内容的重难点，可以说函数是数学的代数知识和几何知识的综合.函数知识的综合性同样体现在函数问题的解题策略上，一般函数综合题有图像法、解析法，以及两者结合使用的综合法，如本题第（3）问的求解，从三角函数的性质来获得解题的突破口，以及变式问题中求不等式的解集采用先分析图像，后分析解析式的方式，均是对上述方法的充分使用，因此充分掌握函数综合题的解法是十分必要的.在实际教学中需要结合考题向学生传达该类题型的解法技巧，使学生深刻体会图像法和解析法在解题中的应用思路.

3.透析表象问题，开展变式学习

函数图像的综合题虽然涉及的知识点多、问题形式多样、图像变化灵活，但实质上就是由基本的函数图像进行的结合，其背后隐含的知识本质是不变的.初中阶段常见的函数有一次函数、反比例函数和二次函数，因此只需要充分掌握上述函数的核心知识即可.另外，在教学中适时地对考题开展变式学习，对考题的问题进行适当改编，利用“形变质不变”的变式问题往往可以加深学生对考题本质的理解，如上述对考题的变式学习，揭露了函数综合问题的核心就是点、线段之间联系性的互化，问题的求解也需要基于此来完成.变式学习不仅是一种学习方式，还可以在求解变式问题中拓展学生的思维，使学生灵活思考，变通解题.

四、写在最后

函数综合题是初中阶段的重、难点题型，虽然其综合性强、复杂度高，对学生的解题思维有着较高的要求，但探寻其本质，同样是众多函数采用一定方式的结合，其中点的坐标是联系各函数图像的纽带.求解时需要充分利用函数解析式，结合函数的相关性质，对问题和条件进行逐步转化，必要时采用适当的解题模式来分析问题，探究解题的突破口.在对函数综合题教学时，首先需要引导学生掌握函数的基本内容，理解函数的知识本质；然后在解题时向学生传达科学的分析方法，使学生形成系统的解题策略，同时适时地开展变式学习，通过考题变式使学生透析问题实质，拓展学生的解题思维，真正掌握函数的知识精髓.

1.沈奕.深入研究揭示结构，归类复习变式再练——以“曲线压轴题”为例［J］.中学数学（下），2017（08）.

2.周红梅.在教学中发展思维，在变式中提升能力——以2016年江苏省泰州市中考第24题为例［J］.中学数学（下），2017（10）.

3.刘志波.活跃在反比例函数中的几何图形［J］.中学数学教学参考，2017（36）.

4.孙海锋，赵韬.反比例函数、一次函数与二次函数综合问题［J］.中学数学教学参考，2018（Z2）.H