巧用几何性质，多解深剖释疑<br/>——以一道平面几何题为例

巧用几何性质，多解深剖释疑
——以一道平面几何题为例

2018-06-23江苏省常熟市海虞中学顾雅玉

中学数学杂志 2018年12期

☉江苏省常熟市海虞中学顾雅玉

对几何考题开展一题多解不仅可以多角度认识问题，挖掘图形性质，还可以拓展解题思路，提升对数学问题的剖析能力.以一道平面几何题为例进行多解剖析，并从挖掘性质条件、夯实知识基础、渗透思想方法等方面开展教学反思，从而引导学生在反思的过程中提升解题素养.

一、问题呈现

1.考题呈现

题目如图1，AB是⊙O的直径，且AB与弦CD垂直于点E，连接CO，并将其延长，交弦AD于点F，已知CF⊥AD，AB=2，试求弦长CD的长.

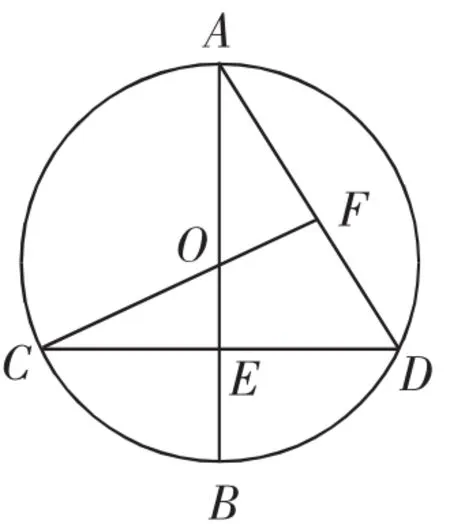
图1

2.思路突破

本题目为初中常见的涉及圆的几何题，主要考查学生三角形、圆等图形的基本知识，整理题干信息可得以下关键条件：有一条直径（AB）；两个垂直关系（AB⊥CD、CF⊥AD）；一条线段长（AB=2）.需要建立条件与待求量CD之间的关系，观察图形可知点A、C、D均位于⊙O上，则连接AC后，△ACD的外接圆是⊙O，利用不同的几何性质即可建立已知与未知之间的关系.

二、解法剖析

圆和三角形存在诸多的性质，利用不同的性质，从不同的角度分析问题，往往可以获得不同的解题方法，以下将具体剖析本题目不同视角下的不同解法.

视角一：利用等腰三角形的“三线合一”

由于题目中存在等腰三角形，可以利用等腰三角形“三线合一”的性质来求解，即等腰三角形中顶角的角平分线、底边上的中线和底边上的高三条线是相互重合的，只需确定其中的一条线即可推得等腰三角形的其他性质.

分析1：在△ACD中，AE⊥CD，由于AB过圆心O，可以推断出AB是CD的垂直平分线，利用垂直平分线的性质可进一步推得AC=AD，则△ABC是等腰三角形，利用CF⊥AD，同理可得AC=CD，则△ACD就是等边三角形，其每个内角都为60°.AB为直径，则半径CO=1，结合“三线合一”性质可推得△COE的内角，进而可得CD的长.

解法1：连接AC，如图2，因为AB⊥CD，且AB过圆心O，则CE=DE，所以AB是CD的垂直平分线，则AC=AD；同理由CF⊥AD可得AC=CD，所以△ACD是等边三角形.由于CF是△ACD底边AD上的中线和高，由“三线合一”可知CF必为∠ACD的平分线，则∠FCD=30°，因为，所以

图2

点评：等腰三角形的“三线合一”既是对三角形特征的一种简单概述，也是一种几何性质，由于涉及角平分线、中线和高，则可以通过确定线段具有其中的一种性质来推得其他几何性质，上述解题思路就是通过确定中线和高来推得等边三角形角平分线的性质，从而打开解题思路的，需要注意的是“三线合一”只适用于等腰三角形，这是使用的基本条件.

视角二：利用三角形“重心”的性质

根据题目的相关条件可以预判图中出现了△ACD的多条中线，则可以利用三角形的重心（三角形三条中线的交点为重心）性质来求解，即重心分别到三角形顶点和对边中点的距离之比为2：1，则可以建立三角形中相关线段的长度关系.

分析2：根据条件可得出AE、CF分别为△ACD的边CD和AD的中线，进而可确定O为三角形的重心，利用重心的性质可得AO、OE的长度，然后在Rt△OCE中，利用勾股定理可得CE的长，从而求得CD.

解法2：因为AB⊥CD、CF⊥AD，且AB、CF均过圆心O，则CE=DE，AF=DF，即AE是△ACD的边CD上的中线，CF是△ACD的边AD上的中线，所以点O为三角形的重心，则AO=2OE.已知在Rt△OCE中

点评：三角形的重心是其三条中线的交点，利用其性质可以实现几何特征向几何元素边长之间的条件转化，由于两条线即可确定一个交点，因此在实际应用中只需要确定三角形任意的两条中线即可，中线的确定方式有很多，可以通过线段的垂直平分线、全等三角形对应边相等，以及圆心对直径的分割等条件来确定，上述解题过程就是利用圆内弦长及相关线段的垂直关系来确定中线的，具体解题时需灵活运用.

视角三：利用菱形的相关性质

题目中存在线段垂直和相等等相关信息，则可以在图形中构造一个菱形，利用菱形的相关性质，如对角线相互垂直且平分、四条边均相等来尝试构建已知条件与待求量之间的关系.构建菱形时需要注意一定的方式，力求利用最少的条件来完成，如先确定四边形是平行四边形，再确定其为菱形.

分析3：连接OD、CB、DB后可以通过三角形全等来证明四边形CBDO为平行四边形，再通过一条邻边相等即可证明其为菱形，利用菱形的性质可以得到线段OE的长，在Rt△OCE中利用勾股定理即可求出CE的长，进而求得CD.

解法3：连接OD、CB、DB，如图3，由已知条件可得△CEO≌△DEB，则OC=BD，∠OCE=∠BDE，可得OC∥BD.因为OC=BD且OC∥BD，可得四边形CBDO为平行四边形.又因为CO=DO，可知四边形CBDO为菱形，可得

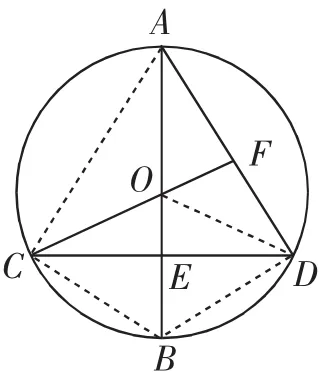
图3

.在Rt△OCE中，CO=

点评：菱形是一种较为特殊的平行四边形，因此其除具有平行四边形的有关性质以外还有一些自身特有的性质，这些性质除可以证明其为菱形以外，也可以用于几何相关问题的证明.一般菱形的证明需要先确定四边形是平行四边形，再通过确定一条邻边相等或对角线相互垂直来完成.

视角四：利用代数方程求解

初中数学最为常见的方法是数形结合的方法，其解题思路是利用直观图形来分析几何关系，然后利用代数的精准性来建立反映几何关系的方程，这种方程就是研究几何问题的一种数学模型，本题目求几何线段，可以设出未知数，利用相关性质来建立关于线段的方程，通过求方程的解来完成.

分析4：可证明△COE和△ADE相似，利用相似性质可建立对应边之间的关系，然后设出未知数CE=x，由勾股定理可得OE，结合相似建立的边长关系可建立一个关于线段长度的方程，解方程后即可求解.

解法4：因为AB⊥CD,CF⊥AD，则∠OCE+∠COE=90°.∠AOF+∠OAF=90°. 又因为∠AOF=∠COE，所以∠OCE=∠OAF，则△COE∽△ADE，则.设CE=x，则，解得，所以

点评：利用代数方程求解实质上是建立了研究几何问题的一种数学模型，其依然是基于对几何图形的关系分析，如上述求解时利用到了三角形相似及勾股定理等性质.代数方程的建立使得问题变得更为简单直接，仅通过方程求解就可以求出线段的长，因此可以有效提高解题效率.

三、反思与启示

1.挖掘性质条件，强化知识理解

初中数学的几何题有着其自身独有的特点，从不同的角度分析问题往往可以得到不同的性质条件，从而获得不同的解题思路，而不同的解题方法往往可以得到同一个答案，实现问题的殊途同归.上述分析线段长分别从三角形的“三线合一”、重心性质、菱形性质和代数方程等角度来求解，均是从不同的角度对问题的分析，其思路是建立在几何性质的充分挖掘上.在实际教学中开展一题多解，不仅是要使学生掌握多种解法，还是为了引导学生多角度的挖掘几何性质，能够灵活运用几何知识来求解，从而强化学生对于知识的理解.

2.夯实基础知识，掌握知识综合

上述的几何问题涉及了三角形、圆等基本的图形，是多图形的交叉组合，求解过程也是对相关性质的综合运用，看似复杂实质解法有迹可循，即充分挖掘问题的基本图形，将复合图形分解为单一的基本图形，然后分别利用图形的基本性质来求解，若图形较为抽象，可以通过添加辅助线的方式，使其变为简单图形.如上述问题的解法均是利用三角形、圆或菱形的性质来求解，均是对基本性质、基本定理和基本方法的综合运用，因此在实际教学中需要引导学生掌握几何提炼的相关方法，夯实基本的单体知识，然后从知识综合性角度出发对单体知识进行综合运用，从而掌握复杂几何问题的解题策略.

3.渗透思想方法，提升解题能力

上述问题的求解涉及了多种方法，解法中同样渗透着多种解题思想，如辅助线的添加涉及了构造思想、图形问题的求解涉及了数形结合思想、代数方程法涉及了方程思想，整个解题过程不仅是方法技巧的运用，同样贯穿着多种思想的活动，是解题的思想方法在指引着问题的转化变形.可以这么说，一题多解不仅是一种方法的多解，也是思想的多解.因此，在实际教学中，要结合具体问题向学生渗透解题的思想方法，使学生在掌握解题策略的同时获得思想上的提升，从而从本质上提升学生解决问题的素养和能力.