知三得所有，聚散解自来——一道初三四月调考题的一题多解得到的启示

☉湖北省武汉市四美塘中学 张 燕

有关圆的相关问题是不少学生的拦路虎，没有思路，无法下笔，对于已知条件不能进行有机整合转换，成为学生的突出问题.事实上，与圆相关的问题大都可以转化为四边形和三角形问题，只需要把圆的背景条件转换入三角形里，进而求三角形的边和角即可迎刃而解.以下就借助对四月调考的一道几何题的分析来揭示出其本质方法.

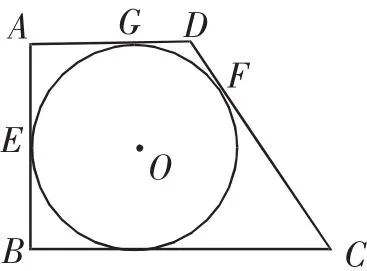
图1

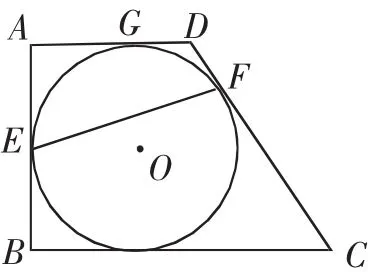
图2

一、原题呈现

（武汉市2018年四月调考第21题）如图1，在四边形ABCD中，AD∥BC，AB⊥BC，⊙O分别与边AB、AD、DC相切，切点分别为E、G、F，其中E为边AB的中点.

（1）求证：BC与⊙O相切，

（2）如图2，若AD＝3，BC＝6，求EF的长.

这里主要研究第（2）问的多种解法，这一问对学生的要求比较高，很多学生拿到题目后犯蒙，笔者结合“知三得所有，聚散解自来”给出具体的方法分析及解法分析.

二、方法分析

求线段的长度，可以归结为两步：第一步，把线段放入三角形中；第二步，在三角形中根据三个已知条件求出线段的长度.我们常用“知三得所有，聚散解自来”这句话来概括这类问题的求解！

知三得所有：对于三角形的三条边和三个内角这六个量，任意给定其中三个量（一般至少含一边），必定可以求出其他三个量（内角的给定和求出，一般指明确其度数或其某个三角函数值）.以下面一个三角形为例：

（1）知三边：AB＝5，AC＝6，BC＝7，根据三边可以通过作垂线，求出三个角的三角函数值，如图3.

图3

图4

（2）知两边及夹角：AB＝4，BC＝5，∠B＝60°，通过作垂线，可以分别求出另外一条边的长度和另外两个角的三角函数值，如图4.

（3）知两边及一边所对的角：AB=5，AC=7，∠B=60°，通过作垂线，可以求出第三条边的长度和另外两个角的三角函数值，如图5.

图5

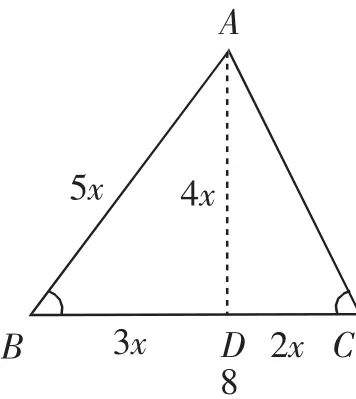
图6

（4）知一边及两角，tanC＝2，通过作垂线，可以求出其他两条边的长度和第三个角的三角函数值，如图6.

“聚散解自来”：一般来讲，根据条件确定“知三”三角形，解“知三”三角形，将得到的边长和角的三角函数值“汇聚”到需求解的三角形中，化“知一、知二”三角形为可解的“知三”三角形.对于复杂问题，往往需要多次求解，多次“汇聚”.求解问题的一般步骤为：

（1）确定“知三”三角形和需求解的三角形（一般是“知一、知二”）；

（2）分析“知三”三角形和需求解的三角形的边角关系（特别是角度的“等、余、补”等关系）；

（3）根据（2）中得到的关系，求解“知三”三角形；

（4）将得到的边长和角的三角函数值“集中”到需求解的三角形中继续求解.

三、具体解题分析

本题的解法有很多种，以下精选了几种不同的构造三角形的方法，以供参考.

解法1：如图7，过C向AD作垂线，垂足为I，过F作FN⊥AI于N，过F作FM⊥AB于M.

可设GD=DF=x，则AG=AE=EB=BH=3－x，进而HC=6－（3－x）=3+x=FC.

DC=DF+FC=x+3+x=3+2x，IC=AB=2AE=6－2x，DI=BC－AD=6－3=3.

在Rt△DIC中，IC2+DI2=DC2，则（6－2x）2+32=（3+2x）2，解得x=1，则DF=1，FC=4.

由NF∥IC，得

则

则

在Rt△MEF中，进而求出EF的值.

点评：解法1将EF放进了△MEF中，并且利用圆的切线长定理及勾股定理，和平行线分对应线段成比例定理求出这个三角形的三个条件：MF、ME和∠EMF，知三求EF的长度.利用了切线里面垂直的特性，构造了直角三角形求解，学生也比较容易想到这些辅助线的作法.

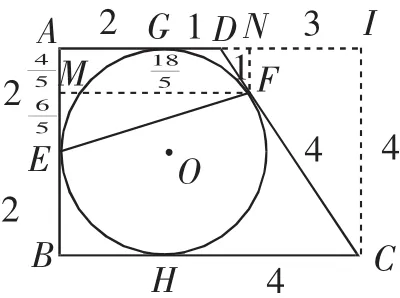
图7

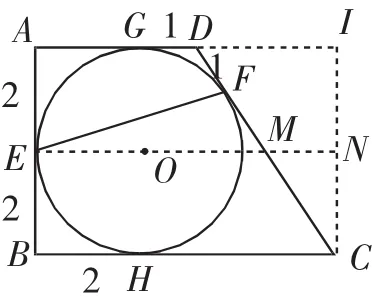
图8

解法2：如图8，连接EO并延长分别与DC、IC交于M、N两点.

则NC=2.

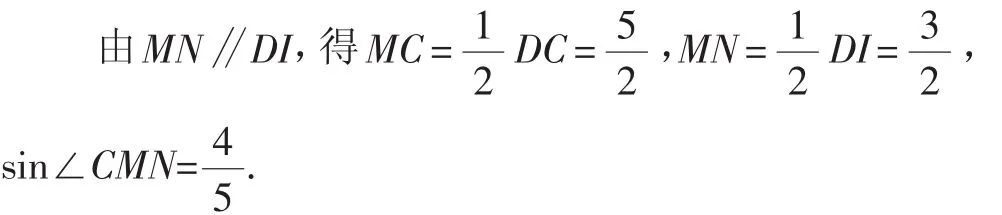
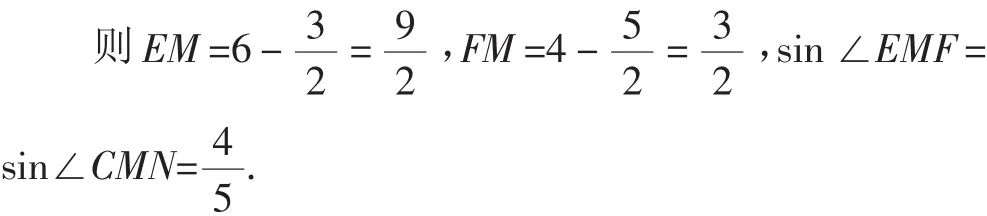
在△EMF中，求出了两条边EM和FM的长度和，便可以利用知三求所有求出线段EF的长度.

点评：解法2将EF构造进△EMF中，虽然不是直角三角形，但根据平行线分对应线段成比例的性质非常容易求得EM、MN的长度，再根据对顶角的转换，得到第三个条件，把条件转换成知三，进而可求出EF的长.将圆的图形转换成矩形、直角梯形，再进一步转换到三角形中求解线段.

上述两种解法是将图形往右边扩展成为一个矩形，利用右边三角形不同边的比例关系转换条件，下面解法3是将图形的重心向下边转换.

解法3：如图9，连接EN、FN、ON、OC、EO.

则，∠EON=90°，则∠EFN=45°.

在Rt△ONC中，利用勾股定理可以求出

利用等面积法可以求得，NF=2MN=

在△EFN中，知道了EN、NF、∠EFN，利用知三求所有，即可解得EF的长.

点评：解法3是将EF构造进△EFN中，通过圆周角等于圆心角的一半可求得∠EFN的值，这是知一；再通过Rt△EON求得EN的长度，完成了知二；又根据切线长定理，在Rt△ONC中求得MN，NF的长度是MN的2倍，可求得三角形的第三个条件，完成知三，即可求得EF的长度.这种解法需要对圆的性质的运用非常熟练，如果能将这个三角形找出，解决这个问题就不难了.

下面两种解法是将图形向上扩展，看起来是同一种解法，实质上不尽相同.

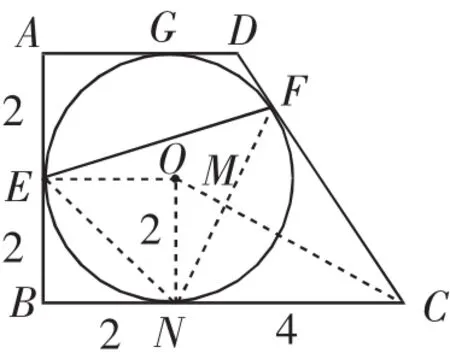
图9

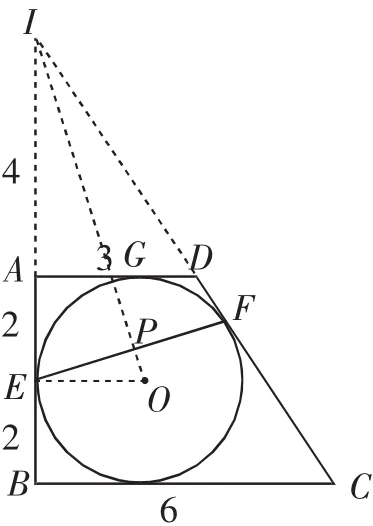
图10

解法4：如图10，延长BA、CD交于点I，连接EO、IO.则IE=IF，IO垂直平分EF.

tanC=

在Rt△IBC中，IB=8，IC=10.

则IE=8－2=6，E0=2.

在Rt△IEO中，由勾股定理可求出IO，再利用等面积法可求出EP的长度，进而EF=2EP，即可解得.

点评：解法4通过平行线分对应线段成比例和切线长定理构造出的直角三角形，先将EF的一半EP的长度求出，再根据EF=2EP，进而求出EF的长度.主要运用直角三角形的等面积法求解EP，学生比较容易想到这种解法.

那么通过解法4的启发，能不能直接通过EF所在的三角形运用知三求所有呢？经过探索，得到了解法5.

解法5：如图11，延长BA、CD交于点I，连接EO、IO，则IE=IF.

tanC=

在Rt△IBC中，IB=8，IC=10，∠I的三角函数值可求出.

在△EIF中，IE=IF=8－2=6，∠I的三角函数值也知道，即可求出EF的值.

点评：解法5相对于解法4来说，就是直接运用知三求所有的思路，把EF构造进△EIF中，根据切线长定理得到它是一个等腰三角形，在大的Rt△IBC中，可以求得∠I的三角函数值和IE、IF的值，把三个条件都求出后，即可解得其他边的长度.

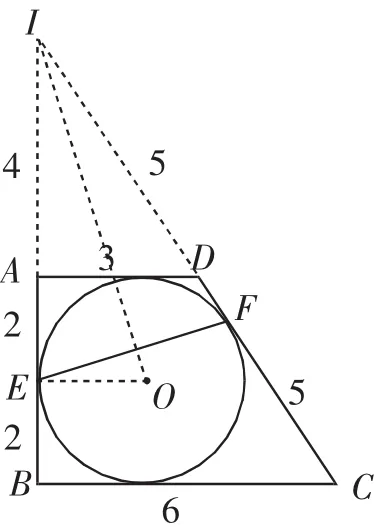
图11

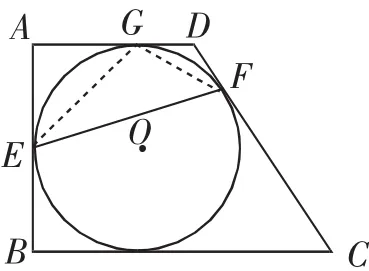
图12

解法6：如图12，连接EG、GF.

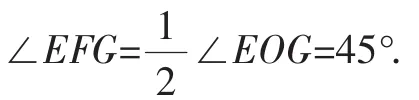
在Rt△AEG中

在△OGF中，GF=OG=OF=2.

在△EGF中，已知三个条件：EG、GF、∠EFG，进而可求出EF的长度.

点评：解法6这种构造三角形的方法很简洁，但是很少有学生想到，因为这不是一个直角三角形，看上去很不好知三，不过两条边EG、GF都非常容易求出，而第三个条件∠EFG，又可以通过圆周角是圆心角的一半得到是45°，那么这个三角形从一无所知到知三求其他，就水到渠成了.

四、总结

以上解法都是通过把EF放入一个三角形，构造出三角形，再把三角形的三个元素求出来（至少要知道一个边），进而求得题目所要求解的问题.知三得所有，聚散解自来.也许构造出的三角形可能一开始一个条件都不知道，通过圆的性质和平行线的性质都能把其他的边或角转化出来，进而达到解决问题的目的.

通过这种方法基本可以解决和圆有关的问题，把圆的有关问题转换成四边形问题，进而继续转换成三角形问题，很好地解决了学生找不到思路、无从下笔的困惑.通过对构造三角形和解三角形的思维过程和解题方法的指导和训练，有助于学生融会贯通，万题归一，灵活应用.F