基于一道例题的设计及教学的思考

☉江苏省张家港市梁丰初级中学 笪艳红

分类讨论，是初中阶段着力渗透的一种数学思想，而培养学生应用分类讨论思想分析和解决问题，则成为了教学的关键.在初中阶段，需要进行分类的数学问题确实不少，尤其在动点问题中，常会因为点的位置不同而带来多种不同的线段长度，这时就需要根据不同的位置关系作图讨论.笔者近期就遇到了这样一道考题，为了培养学生进行分类讨论的意识，通过改编调整呈现了可从数形两个角度形成分类路经达成问题解决的目标，现结合本题的改编及教学历程，谈谈笔者的具体做法，不当之处，敬请批评指正.

一、例题及设计

1.原题及分析

原题如图1，已知抛物线y＝ax2＋bx＋c过点A（－1，0），B（3，0），C（0，3），M、N为抛物线上的动点，过点M作MD∥y轴，交直线BC于点D，交x轴于点E.

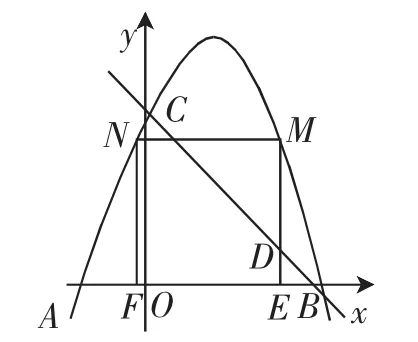
图1

（1）求二次函数y＝ax2＋bx＋c的表达式；

（2）过点N作NF⊥x轴，垂足为点F，若四边形MNFE为正方形（此处限定点M在对称轴的右侧），求该正方形的面积；

（3）若∠DMN=90°，MD=MN，求点M的横坐标.

分析：（1）用待定系数法即可顺利求解.（过程略）

（2） 设M（m，－m2＋2m＋3），则ME=|－m2＋2m＋3|，MN=2m－2.根据“四边形MNFE为正方形”可得ME=MN，即|－m2＋2m＋3|=2m－2，分类求解可得结果.

（3）先求出直线BC的解析式，设点M的坐标为（a，－a2＋2a＋3），则点N（2－a，－a2＋2a＋3），点D（a，－a＋3），类似于第（2）问，可以将线段MD、MN用含有字母a的式子表示出来，再利用MD=MN列出方程，根据点M的位置分类讨论求解可得.

2.例题及分析

例题如图1，抛物线y=－x2＋2x＋3与x轴交于A、B两点（A在B左侧），与y轴交于点C.点M、N为抛物线上的动点，过点D作MN∥y轴，交直线BC于点D.若∠DMN=90°，MD＝MN，求点M的横坐标.

分析：因为需要所以改编，例题设计应紧扣教学需求进行.本例题只选取了原题中的第（3）问作为探讨话题，改编过程中，笔者删去原来的第（2）问，把第（1）问的结果直接告知学生，这样的设计，突出了分类讨论思想的应用，淡化了那些与教学内容关联不大的考点，让核心知识的地位与价值凸显出来，为学生充分体会分类讨论的不同路径及其应用价值留出充足的时间和空间.

二、教学简录及简析

1.教学简录

师投影例题，请学生自主解答，然后在小组中交流答案和解题思路.15分钟后，小组交流结束，教师组织学生全班交流.

师：说说你们的求解思路吧！

生1：我先设M（m，－m2＋m＋3），再根据M、N、D的位置关系分别表示出N点和D点的坐标为N（2－m，－m2＋m＋3），D（m，－m＋3）.

师：接下来，你是怎么做的呢？

生2：由于题目给出了MD=MN，所以我想用含有m的式子把这里的MD=MN表示出来，从而列方程求解.

师：太棒了！看来你已经很好地掌握了方程思想，那我们该如何表示这里的MD和MN呢？

生3：因为不知道M、D的具体位置，所以MD的长度有可能是（－m2＋2m＋3）－（－m＋3），也可能是（－m＋3）－（－m2＋2m＋3）.

师：看来是要分类讨论哦！

生4：对的. 当M在D的上方时，MD＝（－m2＋2m＋3）－（m＋3）＝－m2＋3m；当D在M的上方时，MN＝（－m＋3）－（－m2＋2m＋3）＝m2＋3m.

师：什么时M会“跑到”D的下方呢？

生5：当M过了图中的C点和D点时，就到了D点下方了.

师：给个具体范围！

生6：当0＜m＜3时，M在D上方；当m＜0或m＞3时，M在D的下方.

师：看来是要分三段喽！

生7：对的！分两类三段：当0＜m＜3时，M在D的上方，MD＝－m2＋3m；当m＜0或m＞3时，MD＝m2－3m.

师：完全正确！那MN的位置确定了吗？需不需要也进行讨论呢？

（学生小声议论片刻，一生起立发表见解）

生8：我觉得也要讨论，M可能像图上这样在N的右边，也可能M在左边，N在右边.

师：是吗？（稍作停顿，你说说理由）

生9：题目没有明确告诉我点M的位置，（老师窃喜，原以为删去第（2）问后，学生会不讨论）所以M可以在整条抛物线上滑动.当M在对称轴左侧时，N就在对称轴右侧，当M在对称轴右侧时，N就在对称轴左侧.

师：有没有道理？

生（齐）：有！

师：那怎么来表示MN呢？

生10：当M在抛物线对称轴左侧，即m＞1时，MN＝2－m=2－2m；当M在抛物线对称轴右侧，即m＞3时，MN＝m－（2－m）＝2m－2.

师：好的！接下来该如何列方程呢？

生11：我觉得，根据m的范围应该分为四段.

师：哪四段？

生12：m＜0，0＜m＜1，1＜m＜3，m＞3.

师：你能再说一遍吗？

学生12重复四段取值，教师利用动画同步演示，在M与D重合，M与N重合的关键位置下，停留了较长时间，让学生感知这些位置的特别之处.

师：怎么样，看清楚了吗？

生（齐）：清楚了！

师：那对应的方程呢？

生13：当m＜0时，m2－3m＝2－2m；当0＜m＜1时，－m2－3m＝2－2m；当1＜m＜3时，－m2－3m＝2m－2；当m＞3时，m2－3m＝2m－2.

师：接下来，会做了吧！

生14：解出所列方程，取范围内的m的值就行了！

师：不错！还有其他思路吗？

生15：我觉得，既然不知道M、N的位置，干脆直接把MN的长度表示为MN=|2－2m|，同样地，MD=|－m2＋3m|，直接列出方程|－m2＋3m|＝|2－2m|，再分类讨论就是了！

师：这个方程（指着板书的方程）有道理吗？

学生安静了片刻，稍作思考后，有学生举手作答：

生16：有道理的！添上绝对值后，不管位置如何，大小如何，长度一定是个非负数，这样列出的方程是符合实际意义的.

师：那怎么解呢？

生17：还是要分类讨论.

师：分几类？

生18：四类.－m2＋3m为非负数，2－2m为非负数；－m2＋3m为负数，2－2m为非负数；－m2＋3m为非负数，2－2m为负数；－m2＋3m，2－2m均为负数.

生19：我觉得分四类烦了，直接分两类就可以了！

师：哪两类？

生20：－m2＋3m与2－2m同号，所以－m2＋3m＝2－2m；－m2＋3m与2－2m异号，所以－m2＋3m＝－（2－2m）.

师：很好！求出解后，要注意什么？

生21：要验证一下，m的值是否能让－m2＋3m与2－2m同号或异号.

师：真棒，接下来，请大家根据刚才的思路订正一下.

……

师：这样的思路分析，给你什么启示？

生22：分类讨论可以从形的角度进行，依据不同的位置关系，通过线段的长度或相关量的不同表示，列出方程求解；分类讨论还可以从数的角度展开，不同的取值，可能会生成不同的方程.总之，分类讨论，想到哪种就用哪种，哪种简单就用哪种.

生23：分类要抓住关键的节点，比如位置变化中的交点或“交线”等，数与式中字母的取值发生变化的时刻等，分类的标准可以不同，但对结果是否在分得范围内进行验证却是一样的，无论从形分类还是从数分类，两种情况下都必须进行.

2.简析

利用分类讨论解决问题，有时会因为分类的标准不同，而带来解题模型和解题路径上的差异.正是这样的差异，才给学生的分析与解决问题提供了多种选择的机会.例题的分类标准原来可以唯一，也就是生3和生4描述的两种MD的可能引出的MN的两种可能，进而生成了基于不同点的位置的四种组合，这是从形的角度展开的分类，标准很清晰，也很直观，对于有一定的空间想象能力的学生来说，看出这四种情形还是大有可能的.所以，当学生给出这四种情形后，教师立即引导他们进行了十分详细的分析，在形、数的每一个拐点处驻足观察与交流，这样的分析交流，对学生理解分类标准，把握分类实质，建构与解答数学解题模型是十分有利的.只不过，作为这样一道例题，每个人都能分得如此精致到位，笔者以为还是不易的，所以，当生15给出“添加绝对值再分类”的方法后，无疑让所有人眼前一亮，这是基于数的不同取值下的分类，最终的两个方程，既有数的绝对值含义的深度应用，又有对方程这一等式所存在的性质的强化体验，这种“数”的维度上产生的分类，强化了形的作用，对那些直观想象能力偏弱的学生是很有用的.教师最后组织的小结交流，无疑是“锦上添花”的壮举，因为有了两个不同的分类标准，对学生来说还是蛮新鲜的，所以他们都有话可说.说得如他们的分类那么“自然得体”，而其积淀下的分类经验，无论是形还是数，不同角度，自有不同的风采，无所谓对错、烦简，只要适用，一切皆好.

三、三点感悟

1.精心选择原题，改编凸显价值

命题是教学的核心工具，现成的例题是很少的，必要的改编是为了突出课时核心所需，笔者认为，在改编上花点时间，耗点精力是值得的.以本文中的这道例题为例，为了凸显课时教学核心——分类讨论思想，笔者在2017年的众多中考压轴题中找出了山东威海市中考卷的压轴题作为原型，将原题第（1）问中的求二次函数的解析式删去直接给出二次函数的解析式，虽然原题第（2）问也有分类讨论，而且其设计应是为原题第（3）问的解答服务铺垫的，但作为教学例题，有了原题第（3）问，第（2）问存在的意义并不大，在反复斟酌后，笔者删去了这里的第（2）问直接将第（3）问作为本题的唯一求解要求并入题目，这样一来，题目简洁了，干扰因素少了，自然探索的重点也就凸显出来了，这在教学中也得到了很好的验证，学生的交流完全围绕着“为什么要分类”，“如何分类”等话题展开，例题设计的成效就此突显出来.这样的教学效果，无疑也为我们的例题设计指引了一个方向，在课时核心上多花工夫.

2.强化解题交流，感悟数学思想

数学思想是隐形的数学知识，它们一般都默默地储存于学生的知识结构之中，是静态的.我们的数学教学不仅要帮助学生获得显性数学知识，诸如数学的基础知识和基本技能，还要帮助学生充分感悟数学的“终极财富”——数学思想，那么，对数学思想的感悟依托何在？解题与交流，解题是学生自主唤醒数学思想和应用数学思想的过程，同样也是学生将数学思想自主建构与完善的过程，要知道，没有个体的主动建构，再有价值的思想也是无力的，我们要加强与数学思想相关的解题训练，通过适量的同类型试题的解答，提升学生数学思想建构应用的能力和水平.此外，我们还应让学生交流.通过师生、生生反复互动交流对话，以唤醒和矫正解题中用到的数学思想，毕竟学生的思维力、想象力、应用力都是有限的.在问题解决中，难免会出现疏漏或不足，所以交流的价值在此就凸显出来了.尤其是在我们学生解题后立即展开的交流活动，对学生数学思想的感悟是十分有效的.

3.适度适量训练，培养应用意识

数学思想的应用意识养成非朝夕之功，需要长期坚持，应有适量的训练、适时的交流和反思.任何一个数学思想的萌芽、成长、成熟、知识网络的融入，都是要经历一个长期的、渐进的养成过程.因而，伴随此过程的必然是丰富的数学思想的提取与应用，经历，只有反复锤炼后，这些数学思想检查真正融入到学生的“数学血液”中去.以本文中重点交流的分类讨论思想为例，小学阶段学生接触并不多，进入初中后，由数轴认知开始，数与形均出现了“两面性”，而绝对值的“单面性”则真正让分类讨论进入到学生视野，此后，数与形的不断发展壮大，到初三时，学生已经经历了近三年的分类磨炼，对这一思想的感悟与应用均已有了一定的深度，要知道，在此过程中，学生经历了大量的与之相关联的数学问题的解答与交流，长期的积淀之下，才形成了本文案例中的娓娓道来，甚至是别样的分类，当然，训练是必需的，但这个量和度还是要各位一线教师根据学情把握，总之，一切应以适宜为前提，不可为了思想而让学生深陷题海，好的初衷，却害苦了学生，得不偿失之事，不做也罢.H