对一道统考题的探究
2018-06-23山东省烟台市莱州市柴棚中学陈风波
☉山东省烟台市莱州市柴棚中学 陈风波
最近,浏览微信朋友圈时,看到一位老同学求助一道初中数学统考题的解法,感觉蛮有意思,写出来与读者分享.
一、感受真题
题目如图1,已知圆O的半径为3,OA=8,P为圆O上的一动点,以PA为边向上作等边△PAM,求线段OM长的最大值.
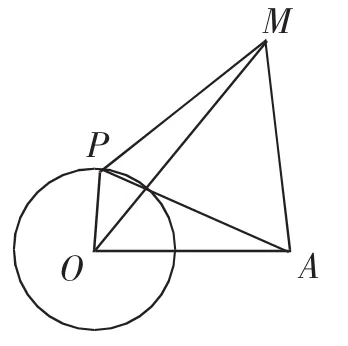
图1
思路分析:由于此题中有“以PA为边向上作等边△PAM”这个条件,可尝试将△MPO绕着点M逆时针旋转,使得MP与MA重合,这样将所求线段OM和已知长度的两条线段OP,OA转化到同一个三角形中或一条直线上去解.
解析:将△MPO绕着点M逆时针旋转,使得MP与MA重合,如图2所示,连接ON.由旋转性质可知,AN=OP=3,OM=MN,∠PMO=∠AMN.因为△PAM是等边三角形,所以∠PMO+∠OMA=60°,所以∠OMA+∠AMN=60°,所以△OMN也为正三角形,所以OM=ON,所以ON≤OA+AN=11.当O,A,N三点在一条直线上且A在O,N之间时,如图3所示,ON有最大值11,即线段OM长的最大值为11.
点评:解答本题的关键是对条件“以PA为边向上作等边△PAM”的处理,由于等边三角形的特殊性,联想到利用旋转变换,将三条线段OM,OP,OA转化到同一三角形中或一条直线上,问题就解决了.

图2

图3
二、追问拓展
拓展1:将题目中“求线段OM长的最大值”改为“求线段OM长的最小值”.
解析:如图2,仍旧将△MPO绕着点M逆时针旋转,使得MP与MA重合,此时在△OAN中,ON≥|OA-AN|=5,当O,A,N三点在一条直线上且N在O,A之间时,ON有最小值5,如图4所示,所以OM长的最小值是5.
拓展2:将题目中“求线段OM长的最大值”改为“求线段OM长的取值范围”.
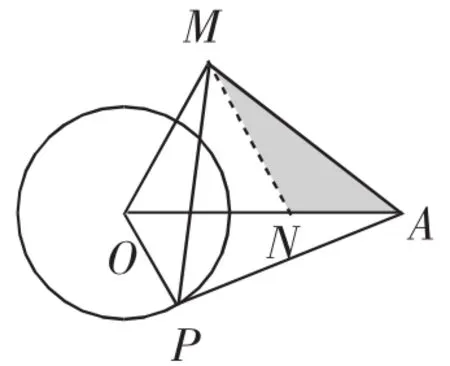
图4
解析:根据真题和拓展1中的解析可知,线段OM长的取值范围为5≤OM≤11,当且仅当O,A,N三点在一条直线上时,线段OM长取到最大值和最小值.
拓展3:若将题目中“以PA为边向上作等边△PAM”改成“以PA为边向下作等边△PAM”,求线段OM长的取值范围.
解析:与真题解法类似,将△MPO绕着点M顺时针旋转,使得MP与MA重合,如图5,连接ON.由旋转性质可知,AN=OP=3,OM=MN,∠PMO=∠AMN.因为△PAM是等边三角形,所以∠PMN+∠NMA=60°,所以∠OMP+∠PMN=60°,所以△OMN也为正三角形,所以OM=ON,所以5=|OA-AN|≤ON≤OA+AN=11,所以5≤ON≤11.当O,A,N三点在一条直线上且A在O,N之间时,如图6所示,ON有最大值11,即线段OM长的最大值为11;当O,A,N三点在一条直线上且N在O,A之间时,如图7所示,ON有最小值5,即线段OM长的取值范围是[5,11].
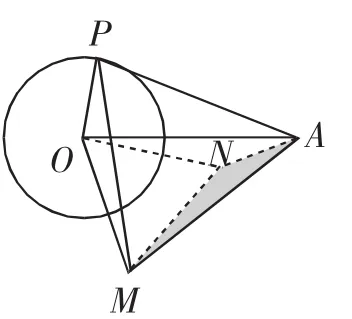
图5
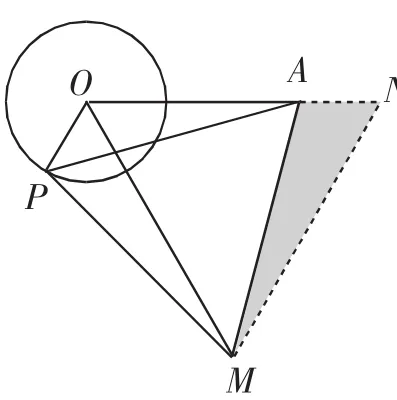
图6

图7
拓展4:若将题目中条件“以PA为边向上作等边△PAM”改成“以PA为底边向上作等腰直角△PAM”,求线段OM长的取值范围.
思路分析:由于等腰直角三角形的两腰相等,对比真题中的等边三角形有类似之处,试想是不是也可仿照以上解法,利用旋转去解呢?
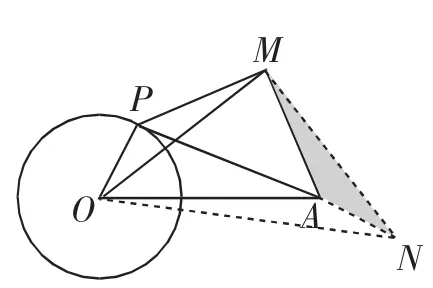
图8
解析:将△MPO绕着点M逆时针旋转,使得MP与MA重合,如图8所示,连接ON.由旋转性质可知,AN=OP=3,OM=MN,∠PMO=∠AMN.因为△PAM是等腰直角三角形,所以∠PMO+∠OMA=90°,所以∠OMA+∠AMN=90°,所以△OMN也为等腰直角三角形,且OM.因为5=|OA-AN|≤ON≤OA+AN=11,所以,所以,当O,A,N三点在一条直线上时,取到等号,如图9,10所示.
图9
图10
三、深入探究
在统考题中,由于所作的是等边三角形,所以通过旋转即可解决所求线段OM的长度,现在,我们再回到问题情境中来,题中点P是定圆O上的动点,过定点A作出的又是特殊的图形——等边三角形,故点M的位置的变化仅依赖于动点P的位置变化,而点P的轨迹是圆O,那么,动点M的轨迹又是什么图形呢?下面就来探究这个问题.
探究1:点P可以看作是由点M绕着点A逆时针旋转60°得到,也就是绕点A逆时针旋转60°得到,以O点为圆心,OA所在直线为x轴建立平面直角坐标系,则A(8,0),可设y0),根据旋转矩阵可得],即由 于 x02+y02=9, 所 以整理有,所以点M的轨迹是以N(4,4为圆心,3为半径的圆.如此,可以作出点M的轨迹,如图11所示,所以OM的最大值为OM1=ON+3=8+3=11,最小值为OM2=ON-3=8-3=5.
我们亦可借助极坐标系来处理:
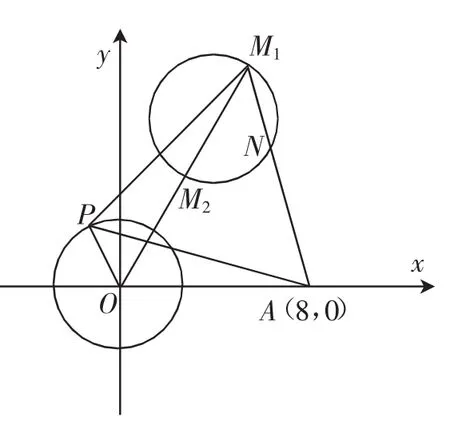
图11
探究2:以A为极点,OA为极轴建立极坐标系,如图12所示,设M(ρ,θ),则∠OAP=120°-θ,OP=3,OA=8,AP=AM=ρ,在△OPA中,由余弦定理可得,OP2=OA2+AP2-2OA·APcos∠OAP,即9=64+ρ2-2×8ρcos(120°-θ),整理有化成普通方程为(x+4)2+,同样得出点M的轨迹是以为圆心,3为半径的圆.如此,可以作出点M的轨迹,如图13所示,所以OM的最大值为OM1=ON+3=8+3=11,最小值为OM2=ON-3=8-3=5.
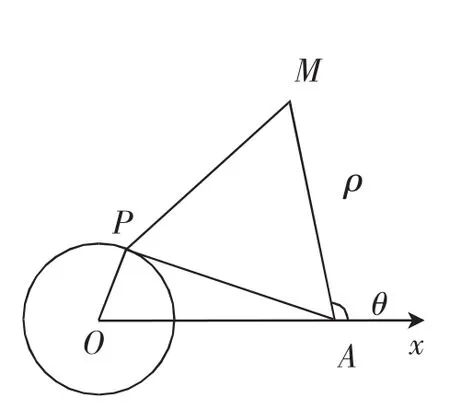
图12
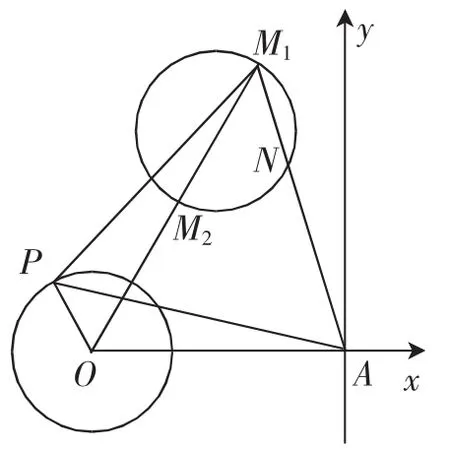
图13
通过以上这道统考题,我们发现,在动点问题中先作特殊多边形,而后求线段长度的问题类型,可以利用旋转的相关性质来解决,也可以先求出动点的轨迹再去解.H
