对“非数学本质伪情境”的商榷——以一节勾股定理应用“青优课”为例

☉江苏省宜兴市洋溪中学 王梨洁

我们知道由中国教育学会中学数学专业委员会主办的全国青年教师初中数学优课展评活动（以下简称“青优课”）是专业领域级别很高的优秀课展评活动，参赛选手和课例一般都是经过层层选拔（县区→地级市→省级）优选产生，拿到全国“青优课”展评时，不仅代表了选手本人、本校的教研实力，更是县区、地市、省级教研团队实力的集中展示．很多高质量的课例及说课稿确实证实了以上分析，然而也有个别课例的教学理念、教学目标的认识、教学情境的“泛化”让人心生疑惑，这样的课例是如何经过层层选拔、打磨，而来到全国赛课平台上的呢？本文以其中一节“勾股定理应用举例”的课例为例，先概述该课，并本着教学研究的兴趣给出商榷意见，提供批评．

一、“勾股定理应用举例”课例概述

1.教学目标

知识与技能目标：了解将实际问题抽象成数学问题，理解利用数学中的建模思想构造直角三角形，探究用勾股定理解决实际问题；掌握已知直角三角形一条边的长和另外两条边的关系，能用勾股定理列出方程．

能力与情感目标：体验学习过程中自身的观察能力、动手能力自学能力、计算能力、逻辑思维能力的发展；经历运用勾股定理知识解决具体问题，提高分析能力和观察能力．

2.说课前准备

教具：教材、电脑、多媒体课件．

学具：用矩形泡沫纸片做成的拱门、小汽车、男孩女孩PK台、笑脸．

3.教学过程

教学环节（一） 巧设问题，引入课题

“大家喜欢旅游吗？”与学生的对话激发学生对勾股定理的应用探知的需求！本节课带领学生到烟台的一座小城去游玩，由第一站护城河引出芦苇题，第二站到博物馆引出旗杆练习题，第三站到美食一条街引出汽车过单行道拱门的题．小热身砸金蛋游戏环节复习常见的勾股数：10以内数字打头的勾股数你知道有谁吗？夯实基础，为应用题的计算快捷提供依据．

教学环节（二） 新知学习

第一站：河边上有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根新生的芦苇，它高出水面1尺.如果把这根芦苇拉向岸边，它的顶端恰好到达岸边的水面，请问这个水池的深度和这根芦苇的长度各是多少？

第二站：学生自做，计时5分钟竞赛.

你想知道博物馆旗杆的高度，而又不能把旗杆放倒测量，当地工作人员发现旗杆顶端的绳子垂到地面还多2米，当他们把绳子下端拉开8米后，绳子刚好斜着拉直下端接触地面，你能算算旗杆的高度吗？

第三站：美食街是个单行车道，你乘坐的车要通过一个拱门，此拱门的截面是一个半径为3.9m的半圆形，你乘坐的车高3.5m、宽3m，你能顺利通过该拱门吗？

教学组织：（1）通过让三组同学开车演示拱门和汽车模型进行分析，通过演示，让学生明白汽车过拱门单行道走中间．（2）学生会根据立体图形画出几何图形，进行合理探究，利用不同方法进行探究．

教学环节（三） 巩固练习，反馈矫正——我就是最棒的

当堂小测验（※为选作题）

（1）一根旗杆在离地面6米处折裂，旗杆顶部落在离旗杆底部8米处.旗杆原来有（ ）米？（A类）

（2）一根16米高的旗杆在某处折裂，旗杆顶部落在离旗杆底部8米处.求断裂处距离地面的高度？（B类）

※（3）想用一条36cm长的绳子围成一个直角三角形，其中一条边长度为12cm，求另外两边的长度．（C类）

教学环节（四） 感悟与反思

通过这节课的学习活动你有哪些收获？师生相互交流总结．

教学环节（五） 布置异步作业（作业略）

本环节分A，B，C类作业．其中A类必做题是基础题，整理错题集是为了提高学生的纠错能力，B类拓展延伸性作业考查学生编题的能力和技巧．

二、课例商榷

应该说，这节课教师的出发点是积极的，试图从有趣情景出发，通过学生探究，运用勾股定理及其逆定理解决实际问题．练习设计时重视变式有梯度，通过一些模仿、表演等活动激发学生参与数学问题解决的兴趣，并注意用分层教学和分层作业，这些都是值得肯定的．然而，从“三个理解”（章建跃博士语，即理解数学、理解教学、理解学生）的角度来看，可提出如下商榷意见．

1.教学目标设定不当，对学段、年级、章节、课时教学目标的辨析不清

章建跃博士在几年前就曾关于教学目标的设定有相关建议，指出了本世纪之初的课程标准中关于三维目标的描述不妥，引发一线教学中对学段、年级、章节、课时目标的设定混乱．从本课例的教学目标来看，也属于典型的目标设定不当，混淆了课时目标与章节目标等阶段性目标，就一节课教学目标来看，提出一些所谓的情感态度价值观的空、泛的目标要求是不适切的，值得商榷．在大会结束阶段的总结报告中，章建跃博士对这类目标设定不当的问题再次提出了批评意见．让人惊讶的是，笔者在查阅这份课例word原稿时，在文本中竟然发现了一个缩小后的图片版某学科资源网LOGO，这让人疑虑的是：这份层层打磨、选拔走上全国“青优课”展台的课例稿难道是从网上直接下载的吗？

2.教学情境设置不当，过分低龄化、缺乏趣味性冲淡了八年级应有的数学味

“数学课要教数学”，是很多专家学者、一线教师的共识、常识．然而作为本课例的主要“特色”，非数学内容本质属性的教学情境选用过多，冲淡和干扰了本课教学主题，比如把一些应用问题通过虚拟学生到某城市旅游，依次进入第一站，第二站，……，再如，教师准备了一些学具：用矩形泡沫纸片做成的拱门、小汽车、男孩女孩PK台、笑脸，这些学具与本课学习的勾股定理的应用并无本质上的联系，属于枝蔓，且对学生理解本课内容会产生干扰作用．这种过分偏重趣味化的情境创设过分低龄化，学生到了八年级的阶段已不需要像小学低学段那样创造这种幼稚的情境，数学的趣味应该更多的来自学科本身，引导学生通过解题、反思、感悟出罗素所指出的“数学冷峻的美”．

3.精心选择数学现实，通过变式改编、拓展生长后串联起不同教学环节

数学现实包括好的数学习题，作为本课训练的是勾股定理与逆定理来看，教材上有很多经典问题都是值得深入挖掘的好题，这里不妨摘选几例进行一些变式改编，提供分享：

题1 如图1，在网格中每个小正方形的边长为1.

（1）计算并找出四边形ABCD的哪一条边最长？

（2）四边形ABCD的4个内角中，有哪个角为直角吗？请找出来，并说明理由.

（3）能求出点A到BC的距离吗？

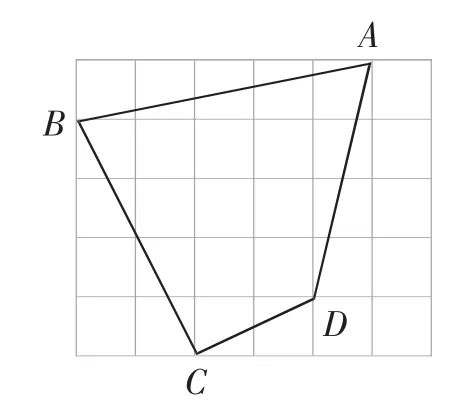
图1

图2

题2如图2，在正方形ABCD中，M是BC的中点，N是CD上一点，且CN＝CD．

（1）若正方形ABCD的边长为4，求AN、MN的长.

（2）有人发现△AMN也是直角三角形．你觉得这种发现有道理吗？

（3）定义：若直角三角形的两条直角边之比为1∶2，称该直角三角形为“半切三角形”．请指出图2中有几个“半切三角形”，并说出依据．

设计意图：题1、题2都是以教材上的经典问题为例，通过“正反设问”把勾股定理与逆定理融入“题”中，指向教学目标，同时又在一个题干背景之下进行系列的设问，帮助学生解一题、会一类．

三、写在最后

数学习题课是一种十分常见和重要的课型，也需要认真研究，习题课并不是拿着练习册、习题单一题接一题的讲评，或是教师仅凭经验即兴变式与链接或拓展（这是章建跃博士批评的“踩着西瓜皮，滑到哪里是哪里”），而需要教师精选习题，深度变式改编拓展，并预设好各个习题与小问呈现的顺序，层层递进、渐入佳境．当然，知易行难，有待我们共同努力，研发有品质、有数学味的习题课教学课例．

1.章建跃．理解数学是教好数学的前提［J］．数学通报，2015（1）.

2.刘东升．我们需要怎样的“问题”驱动课堂——由美国莎维女士执教的函数图像课说起 ［J］．教育研究与评论（课堂观察版），2016（11）.

3.明知白．解题教学重在解题策略和思路的引导与探究［J］．数学通报，2018（1）.

4.汤义佳．内容效度：课时例、习题选编的重要指标——以九年级新授课学案的研制为例［J］．中学数学（下），2017（9）.H