基于能力谱的桥墩冗余度评估

2018-06-22沈利来缪卫清常军

常州工学院学报 2018年2期

沈利来，缪卫清，常军

(1.苏州科技大学土木工程学院，江苏苏州 215011；2.苏交科集团股份有限公司，江苏南京 210019)

早期结构抗震设计大多以承载能力来控制结构性能，而且只要满足承载能力，便可认为能够保证结构在地震作用下的安全性能[1]。随着对弹塑性反应结构的深入研究，设计人员认识到，承载能力不能全面反映结构损坏程度的变化，也很难评估结构的抗震安全性，而结构的变形能力和损坏的程度密切相关，变形能力缺乏往往是结构倒塌的主要原因[2]。

基于性能的抗震设计出现在20世纪90年代，美国加州大学伯克利分校的J.P.Moehle建议改进基于承载力的设计方法，提出基于位移的抗震设计理论，要求考虑结构的塑性变形能力，以满足预定的地震作用下的变形[3]。由建筑物的重要性和用途确定其性能目标，提出不同的抗震设防标准，使设计的建筑物在未来地震中具备预期的功能。这一理论思想影响了美国、日本和欧洲土木工程界，并应用于桥梁的抗震分析中。随着该设计理论的发展，建立了基于结构性能评估的结构设计体系[4]。

桥梁抗震设计，其主旨是保证“能力”适度大于“需求”。在特定设防水准下，桥梁构件的地震响应可以认为是结构要求,而结构本身所具备的抗力和容许延性组成结构自身的“能力”[5]。因此，弹塑性阶段结构的延性是评价桥梁抗震性能的一个重要指标。Freeman等人在1975年提出基于弹塑性分析的能力需求谱方法，通过比较结构的能力谱和地震响应谱，对地震作用下结构的非线性响应特征进行定量分析。该方法在ATC-40正式报告中被重点推荐用于结构抗震性能的评估和设计[6]。为了更加有效地评估结构安全性，本文在上述研究的基础上，结合冗余度的概念分析结构的抗震性能。文中采用数值模拟和试验相结合的方法进行桥墩抗震性能的冗余度评估研究。

1 能力谱方法的原理

能力谱方法主要是通过谱曲线图形，将结构本身的能力和地震响应对结构的要求进行比较。将由Pushover分析得到的结构基底剪力与顶部位移曲线转化为能力谱曲线，并根据相同图形上的加速度响应谱通过A-D转换获得需求谱，能力谱上性能点随即确定，可通过数值计算或者图解法算出。能力谱和需求谱曲线的交点即为性能点也称为目标位移点，表明地震激发下的结构、位移峰值和相应的加速度响应[7]。

设A为反应谱加速度，D为需求谱位移。底部剪力Vb和弹塑性分析的顶部位移uN之间的关系是根据下列方程转换的：

(1)

其中，

(2)

式中：mj表示第j层的质量；φj1表示第1振型在第j层的振幅；φn1表示第1振型向量中对应于第n个质点的元素，第1振型向量按顶点向量位移为1正则化；Γ1表示第1振型参与系数。如图1所示。

图1 能力谱转换

所谓A-D转换，即将标准的加速度反应谱按下式转换为地震需求谱：

(3)

式中Tn为结构的周期。以D为横坐标，A为纵坐标绘出曲线，称为地震需求谱[8]。如图2所示。

图2 地震需求谱转换

将能力谱和地震需求谱绘制在同一图中，然后将结构振动周期和等效黏滞阻尼逐步校正，执行一系列等效线性系统的迭代分析，以确定结构的性能点。找到了结构的性能点，即可评估结构的抗震安全性[9]，如图3所示。

图3 确定结构的目标位移

2 桥梁冗余度

2.1 桥梁冗余度概念

桥梁冗余度，是指一个桥梁的上部结构在其构件损伤或者失效后，不发生倒塌性破坏，继续发挥其功能的能力[10]。每个桥梁结构都是一个结构系统，不能单纯考虑构件的作用，要从桥梁结构整体角度对不同功能构件进行连接，构成结构受力体系，确保桥梁整体承载能力。一座缺少冗余度的桥梁，其安全系数较低，某一构件破坏或者是连接失效，整体稳定性必将受到影响。而一个冗余度较高的桥梁在整体失效前，必定有两种以上的构件(或连接)失效，单一构件遭到破坏不会影响整体稳定性。因此，很有必要在桥梁设计中引入冗余度的概念[11]，以保证整体结构的多重传力途径，增加桥梁结构承载能力的储备率。

2.2 冗余度的定量指标

基于冗余评估确定结构性能，学者们提出了一些指标，如承载力、位移、能量、结构反应灵敏度。本文旨在研究地震作用下桥墩构件的冗余度定量指标，因此选取其中承载力和位移两个指标来进行冗余度的定量分析评估[12]。

2.2.1 基于承载力的冗余度指标[13-14]

20世纪80年代，Frangopol、Moses和冯元生等先后提出将表征结构损伤前后整体承载力变化的各种指标作为结构冗余度的测度。其中，储备强度比定义为完好结构的承载力Vu与设计承载力Vd的比值，用RSR表示。

(4)

2.2.2 基于位移的冗余度指标

类似于位移延性系数的概念(位移延性系数[15]是墩顶最大位移与上屈服位移之比，该系数越大，强震下的结构就越能承受大的塑性变形而不破坏塌陷)，位移冗余度ηu定义为

(5)

式中，um为最大位移，ud为目标位移。

本文将NCHRP报告406中推荐的Rd冗余度量化指标作为理论基础[16]，结合相关学者的研究成果，对冗余度量化指标进行改进。结合桥梁的抗震性能特点，将公式(4)、(5)中的Vu和um用结构的极限能力值φm替代，Vd和ud用结构在地震作用下不发生倒塌性破坏的目标需求值φd替代，冗余度需求值公式为

(6)

3 算例分析

本文采用有限元软件建立桥墩非线性FEM模型，采用Pushover分析得出结构的能力谱和地震需求谱，从而分析桥墩上沿不同墩高各构件的冗余度需求，其中包括横桥向和纵桥向的冗余度需求，具体的定量冗余度指标包括位移和承载力。

3.1 建立模型

本文将实际结构做了简化，模型中只建立了桥墩和盖梁的模型，墩底固结，盖梁与桥墩之间的连接为弹性连接。桥墩和盖梁的材料均为C50混凝土。盖梁和桥墩的截面形状和尺寸见表1。上部结构的恒载用集中荷载模拟(图4)。

表1 截面数据 m×m

图4 结构模型

配筋及相关材料参数详见图5和表2—4。

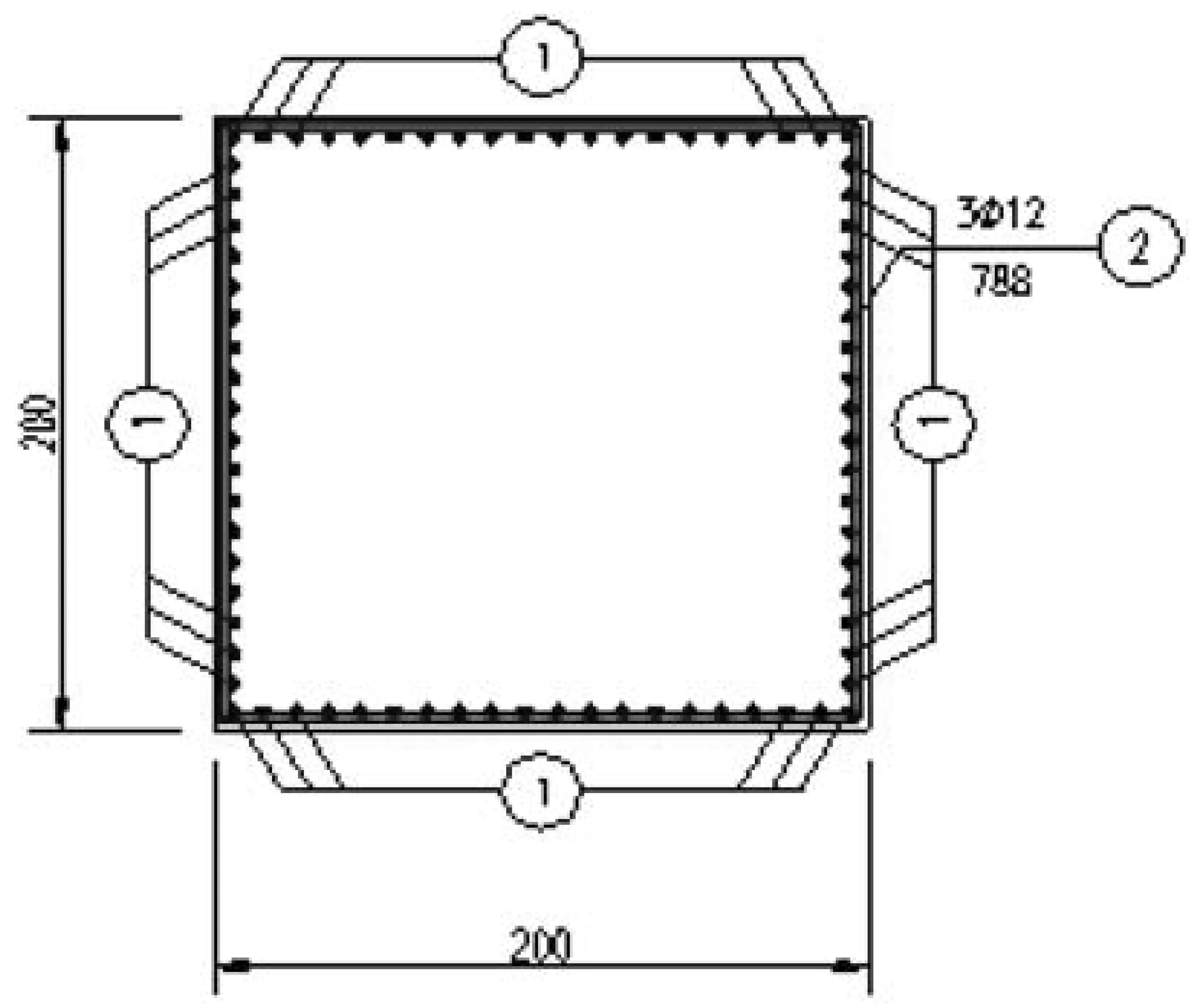
图5 墩柱钢筋图(单位：cm)

表2 墩柱钢筋明细表

表3 混凝土的特性值

表4 钢筋的特性值

3.2 Pushover分析

确定初始荷载，比例系数均为1，在应用Pushover荷载前，初始荷载就已经作用于结构。荷载详细信息见图6和表5。即，当恒荷载被定义为初始荷载，且同时进行一种横向荷载工况的Pushover分析时，我们能够评价在恒载和横向荷载组合效果下结构的反应能力、非线性分析选项参数的设置等。

本例采用“位移控制”，按照不同桥墩高度依次选取4个主节点，分别进行分析。主节点分别为2、5、9、15号节点，详见图4中节点位置编号。主节点在X和Y方向的最大位移为节点结构高度的2%。X方向为纵桥向，Y方向为横桥向。初始的目标位移一般可假定为结构总高度的2%～4%，荷载模式分为模态、静力荷载工况和加速度常量。本例选择加速度常量作为荷载模式。

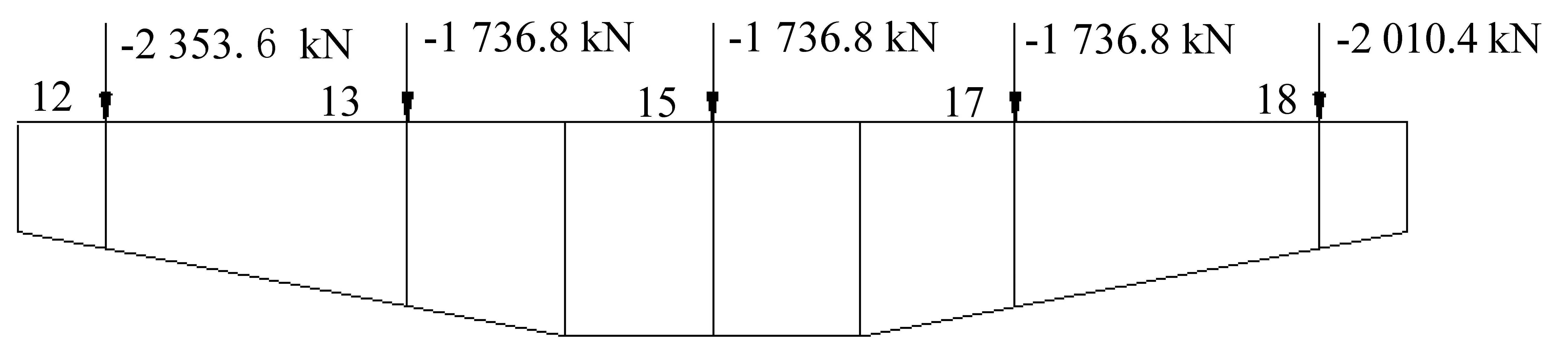
图6 上部结构恒载作用在盖梁上的位置

表5 荷载数据 kN

4 桥墩结构冗余度需求评估

通过以上Pushover分析可得出结构的能力谱曲线，再定义设计生成反应谱，设计时选用《铁路工程抗震设计规范》(GB 50111—2006)，设计地震分组为1，场地类别为Ⅱ，设计特征周期为0.35 s，地震设防烈度为8度，设计基本地震加速度为0.20g，地震影响选择罕遇地震，基本水平地震加速度为0.38g，桥梁的重要性选项为重要桥梁。

根据能力需求谱，找到性能点，确定目标位移以及该位移下的基底剪力值等参数。图7、8为主节点15号节点位移控制下的能力需求谱。

图7 主节点15号X方向能力需求谱

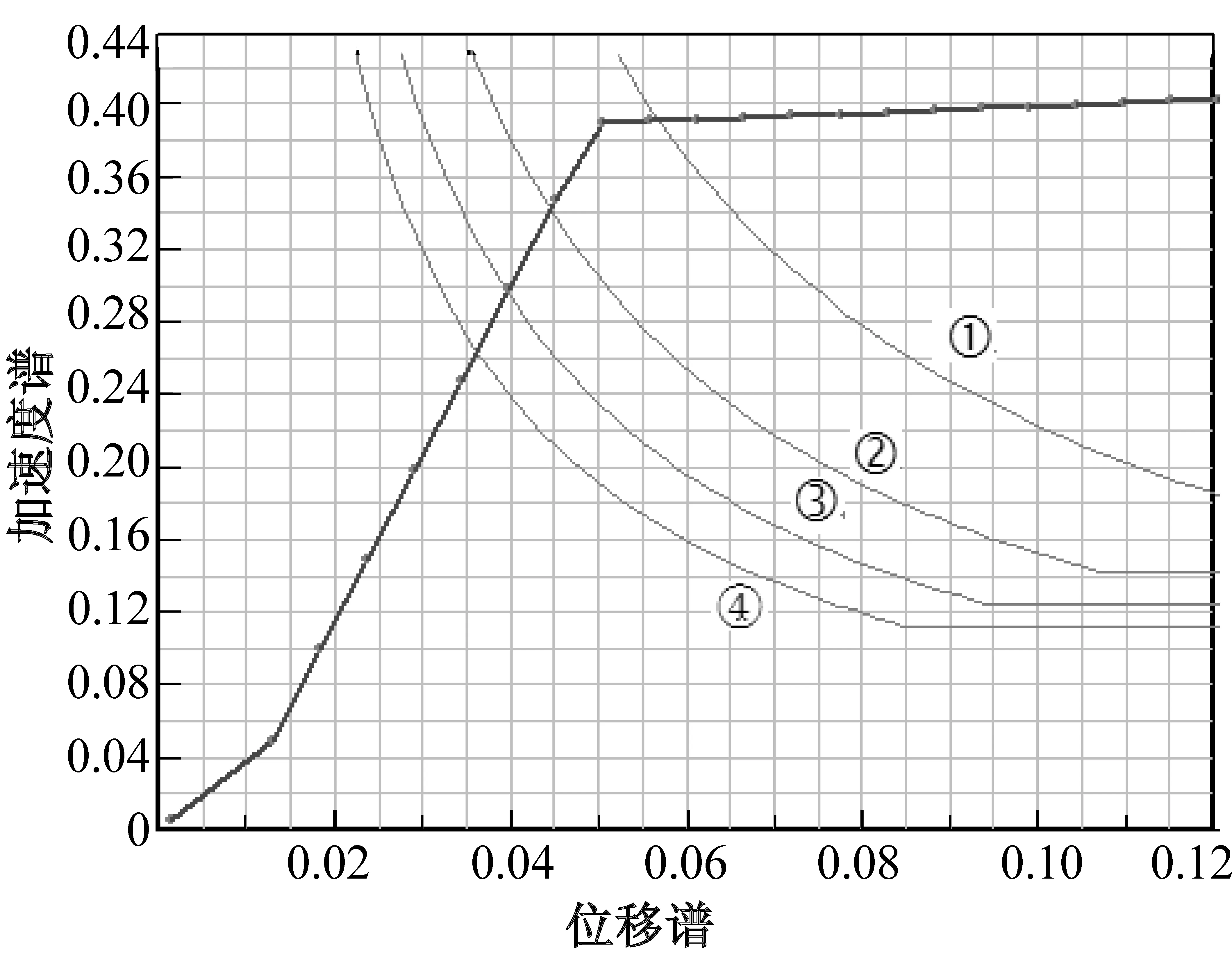
图8 主节点15号Y方向能力需求谱

如图7、8所示，从原点出发的曲线代表结构的能力谱曲线；标有数字①、②、③、④的曲线则代表在不同阻尼比下的地震需求谱曲线，①—④的需求谱曲线依次为5%、10%、15%、20%的阻尼比需求谱。本例中选择罕遇地震作用下5%阻尼比的需求谱与结构的能力谱的交点为结构的性能点。4个主节点的性能点数据见表6。

表6 主节点的性能点数据

根据表6中的性能点的具体数据，结合冗余度的定量计算指标，参照公式(6)即可计算在地震荷载作用下，保证结构不倒塌时的冗余度需求值。详见表7。可以看出，桥墩上不同高度处，冗余度的需求值是不同的，且随着高度的增加，桥墩的冗余度需求值逐渐减小，表明桥墩结构越往下，其重要性越大，墩底需要更多的强度储备。由表6可见，墩顶的位移值远大于墩底的位移值，这表明墩顶需要更多的刚度储备。由表7可见，纵桥向相对于横桥向的位移冗余度需求值更大，表明纵桥向在地震作用下易发生过大位移导致落梁等灾害。承载力方面则相反，横桥向的冗余度需求值更大，表明横桥向需要更多的强度储备以防止侧翻等灾害。

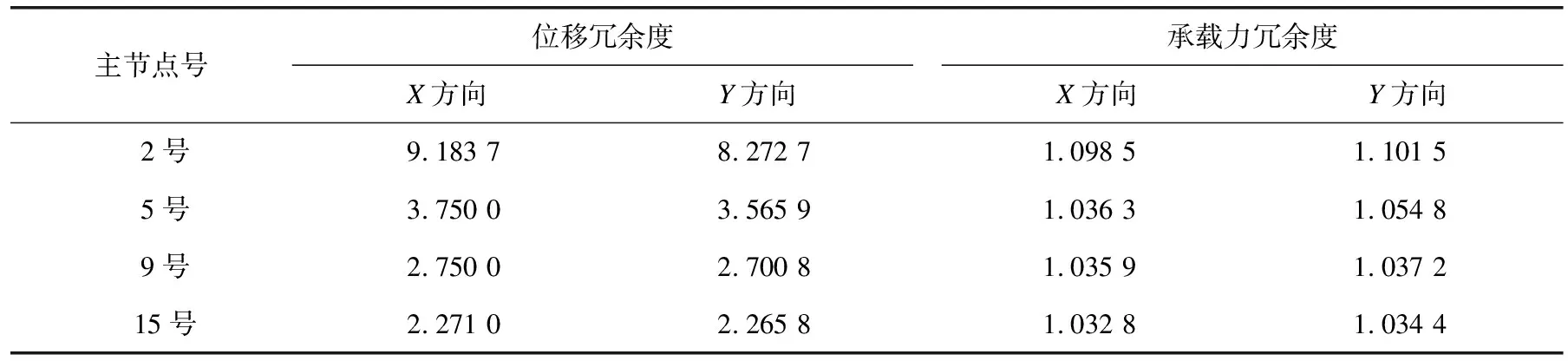
表7 节点构件冗余度需求值

5 试验分析

5.1 试验系统介绍

试验采用的墩柱为1∶10的缩尺模型。墩柱的配筋图见图5，钢筋信息见表2，考虑缩尺效应，参照《混凝土结构设计规范》(GB 50010—2010)将3.1中的节点动力荷载乘以1.35的系数。

本试验采用DSPACE-FTS试验系统，如图9所示，该系统结合了DSPACE控制台和FTS液压伺服驱动器，可以自主编程和进行有限元计算。

图9 DSPACE-FTS混合试验系统

高压油从液压源的油泵输出，经过分油器进入电液伺服阀，然后输入到双向作动器的前后油缸内，通过液压差驱动作动器运动到指定位移处或者对试件施加所需荷载。桥墩运动方程数值计算中的参数、作动器控制参数的调节均采用Simulink模块的形式编写程序，利用RTW/RTI进行控制并下载至DSPACE组件中，通过A/D转换器将作动器上的传感器传来的电信号转换为数字信号。根据观测的位移和力数据，修正桥墩的刚度，然后将修正的结构刚度带入运动方程求解得到的结构位移，再由D/A转换器转变为电压信号，通过驱动作动器来实现位移加载，以此循环往复。

采用变幅等幅混合的位移控制加载制度，详见图10，纵坐标表示屈服位移的倍数，横坐标表示加载周次。