基于弹性中心的客车动力总成悬置系统布置

2018-06-22李智强张攀登黄美婷

常州工学院学报 2018年2期

李智强，张攀登，黄美婷

(1.福建船政交通职业学院，福建福州 350007；2.同济大学机械与能源学院，上海 200092)

汽车动力总成是车内主要振动来源之一，汽车动力总成悬置系统隔振性能的好坏对汽车的乘坐舒适性非常重要。动力总成通过橡胶软垫安装在车架上，构成一个六自由度的振动系统。悬置系统需要有好的隔振性能，系统的自然频率要避开激励频率，同时要减小各阶模态之间的耦合。目前，广泛采用的方法是建立优化模型对各阶模态解耦进行数值计算[1]。不同于轿车，客车采用订单式的销售模式，设计周期短，给不同配置的同款车型匹配悬置系统时采用数值优化有一定的盲目性，工作量大，效果差。本文根据客车动力总成悬置系统一般相对于曲轴左右对称的特点，应用弹性中心理论，对悬置系统进行解耦布置，方便快捷，为同车型不同配置的客车悬置系统设计提供参考。

1 悬置系统的解耦设计

将动力总成和车架假设为刚体，不计悬置元件本身的重量，动力总成悬置系统简化为一个六自由度振动模型[2]，如图1所示。建立发动机质心坐标系O-xyz，原点O在质心，x轴平行曲轴指向发动机前端，z轴与气缸平行竖直向上，y轴由右手定则确定。定义系统振动的广义坐标系为x=[x，y，z，θx，θy，θz]T，系统的自由振动方程为

(1)

式中,M为系统质量矩阵，K为系统刚度矩阵。

求解式(1)特征方程K-ω2M=0的根即为系统的固有频率。

图1 动力总成悬置系统模型

系统的解耦率从能量的角度进行求解，系统在第i阶模态振动时，沿着主振动方向(第k个广义坐标轴方向)的解耦率为该方向的振动能量与外力(力矩)做功的比值，其表达式[2]为

(2)

式中，Φi为第i阶振型向量，mkl为质量矩阵第k行第l列元素，Φik、Φil分别为第i阶振型第k个和第l个元素。i、k、l均为1，2，3，…，6。

2 客车悬置系统弹性中心解耦

2.1 扭矩轴的计算

刚体无约束状态时，向刚体施加扭矩，刚体将围绕扭矩轴转动，扭矩轴由动力总成的惯性参数和扭矩的施加方向决定[3]。在汽车上，动力总成受到悬置的约束，当发动机运转时，动力总成受到绕曲轴中心的扭矩作用，这时动力总成近似绕着扭矩轴振动，扭矩轴通常不与惯性主轴和曲轴中心线重合，如图2所示。

图2 动力总成悬置布置图

扭矩轴在发动机质心坐标系的方向可以通过计算得到[4]，构造质心坐标系下惯性矩的二阶张量

(3)

假设

(4)

k为矩阵ST-1第1列的规则化常数。扭矩轴在质心坐标系下的方向余弦向量[4]可以表示为

qTRA=[αxT，βxT，γxT]T

(5)

2.2 弹性中心的解耦布置

弹性支撑的刚体，沿着某轴线受到力或力矩作用时，如果只发生该方向的平动或转动，那么这条轴线被称作弹性轴，弹性轴由弹性体的刚度和位置参数决定，与刚体的参数无关[5]。客车大部分采用发动机后置纵置的布置方式，悬置一般相对于发动机曲轴中心线对称布置，两个前悬置在发动机前端，两个后悬置在飞轮壳或者变速器上。前后悬置通常按照一定角度布置，并且左右悬置表面的法线平面垂直于曲轴中心线时，前后悬置的弹性中心连线就是弹性轴，如图3所示。

图3 前悬置截面

对称安装的悬置系统，弹性中心位于曲轴中心线上方，在高度方向距离悬置安装平面的距离[5]为

(6)

式中：E为悬置距离曲轴中心在y方向的距离；θ为悬置的安装角；λ为橡胶悬置剪切比，λ=kw/kv。

对于三维空间非对称的动力总成，悬置系统要实现完全解耦是不可能的，因此动力总成悬置系统的设计主要考虑提升解耦的程度。通过调整悬置元件的刚度和角度，使得前后悬置的弹性中心在扭矩轴或其附近实现主要振动方向(垂向z和绕曲轴的转动方向θx)的解耦[6]。另外，如图4所示，前后悬置满足式(7)时，前后悬置的振动互不影响，可以提高θy方向的解耦率。

图4 前后悬置布置示意图

kzfLf=kzrlr

(7)

式中，Lf为前悬置到质心的距离，Lr为后悬置到质心的距离，kzf为前悬置在垂向的等效刚度，kzr为后悬置在垂向的等效刚度。等效刚度的计算公式为

kz=kvsin2θ+kwcos2θ

(8)

式中，kv为v方向的刚度，kw为w方向的刚度。

根据上述对弹性中心的解耦分析，调整弹性中心解耦方式可以通过如下方式实现：1)悬置元件向上移；2)减小悬置软垫安装夹角；3)悬置元件向外(两侧)移；4)改变悬置元件刚度；5)综合上述几种方式。可以根据悬置的布置空间选择调整方式，在编写好的程序上进行参数调整时可以即时得到调整结果，方便快捷。

3 设计实例

3.1 原系统的解耦率计算

根据上述设计理论分析，选某款中巴车动力总成悬置系统为设计对象。订单车的动力总成与标配车不同，经测试，订单车的动力总成惯性参数为：质量m=823 kg；转动惯量Ixx=46.2 kg·m2，Iyy=158.7 kg·m2，Izz=141.9 kg·m2；惯性积Ixy=-1.2 kg·m2，Iyz=0.69 kg·m2，Izx=27.42 kg·m2。

经计算，扭矩轴在动力总成质心坐标系的方向角见表1。

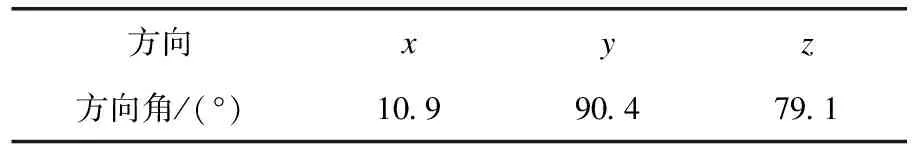
表1 扭矩轴方向角

扭矩轴和前后悬置所在的切面分别交于M和N点，如图5所示。M点到前悬置水平面的高度为HfTRA=220.5 mm，N点到后悬置水平面的高度为HrTRA=323 mm。

图5 扭矩轴的位置

在标准配置的悬置系统中，悬置元件按45°安装，在质心坐标系的位置见表2。

表2 悬置元件坐标 mm

前后悬置的三向刚度见表3。

表3 悬置元件的刚度

标配的悬置系统优化前固有频率和解耦率见表4。各阶振动的频率满足要求，但是各阶振动的耦合较为严重。

表4 优化前悬置系统的固有频率和解耦率

经计算，前悬置弹性中心到前悬置水平面的距离为Af=161 mm

3.2 弹性中心优化及解耦计算

根据3.1的分析，订单车动力总成变更后采用标配悬置系统的解耦性能较差，需要在原来的基础上进行调整优化。按式(6)和式(7)分别编写程序，根据设计的范围逐个调整参数，直到满足要求。

优化结果为：前悬置(x，y，z)方向刚度为(110,138,553)；左右悬置向外(两侧)移动34 mm；安装角度调整为30°；调整后弹性中心高度Af=220.6 mm，近似与HfTRA相等；后悬置垂直向上移动100 mm；调整后弹性中心近似在扭矩轴上。同时，前后悬置的刚度满足式(7)的关系。优化后得到系统的固有频率和解耦率见表5。