IGSA-LSSVM软测量模型预测燃煤锅炉NOx排放量
2018-06-22丁知平牛培峰清远职业技术学院信息技术与创意设计学院广东清远550贵州航天电器股份有限公司贵州贵阳550009燕山大学工业计算机控制工程河北省重点实验室河北秦皇岛066004
丁知平, 刘 超, 牛培峰(. 清远职业技术学院 信息技术与创意设计学院, 广东 清远 550; . 贵州航天电器股份有限公司, 贵州 贵阳 550009; . 燕山大学 工业计算机控制工程河北省重点实验室, 河北 秦皇岛 066004)
1 引 言
近年来,随着我国对环境污染治理的重视,降低NOx排放量是火力发电厂生存的客观需要,因此要建立计算模型预测NOx排放量[1~3]。
神经网络和支持向量机[4]等人工智能技术因其良好的处理非线性的能力,可较好地解决NOx建模问题,但神经网络往往出现过拟合和泛化能力弱等不足,支持向量机在NOx排放建模方面受到越来越多的关注。NOx排放预测问题由于具有复杂非线性、多维多模、数据样本少等特征,且需要解决结构风险最小化问题。最小二乘支持向量机(least squares support vector machine,LSSVM)[5]是一种优秀的学习方法,LSSVM训练过程中需要确定模型的“超参数”以建立有效的预测模型,如何获得最优的超参数是NOx排放量模型精度的关键。事实上,LSSVM超参数的调整过程也是参数优化的过程,基于LSSVM与寻优技术结合的燃烧优化是降低锅炉NOx排放的一种有效途径[6,7]。
引力搜索算法(gravitational search algorithm,GSA)[8]是由Esmat Rashedi等人提出的一种源于对万有引力定律进行模拟的智能优化技术,因其具有概念简单、易实现等特征而得到广泛应用[9,10]。然而,GSA在高维多模函数优化中存在优化能力弱的问题,为进一步改善算法的优化性能,本文提出了一种改进的GSA算法(improved GSA, IGSA),在IGSA算法基础上,建立了基于IGSA-LSSVM的NOx排放量软测量模型。
2 GSA算法基本原理
(1)
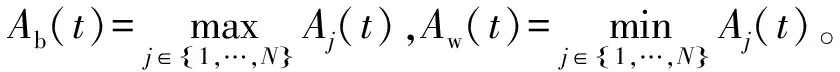
在特定的时间t,作用在质点j和质点i之间的引力定义为:
(2)
式中:Mi和Mj为质点的质量;ε为一较小的常数;Rij(t)为质点间的距离;G(t)为引力系数。则作用在第i个质点的第d维上的合力为:
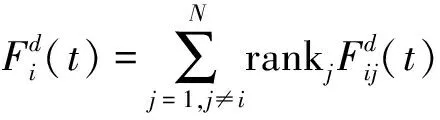
(3)
式中:rankj为[0,1]中的一个随机数。
根据运动定律, 在时间t质点i的d维加速度为:
(4)
在GSA算法中,按式(5)更新质点的速度和位置:
(5)
3 改进的GSA算法
GSA算法虽然有较优异的优化性能,但在处理部分复杂优化问题时,GSA仍然存在早熟收敛、易陷入局部最优解的缺点。因此,其寻优能力仍需进一步改善。
3.1 基于网格算法的初始化种群
GSA算法的第一步就是初始化种群,一个较好的能够覆盖整个解空间的初始种群有助于改善进化速度和提高解的质量。如果包含全局最优解的局部解空间不在初始群空间,同时质点的位置更新算法又不能在有限次数的进化过程内将覆盖空间扩延到全局最优解所在的区域,那么过早收敛就不可避免,可以看出,初始种群个体的分布状况直接影响算法的全局收敛性能。针对原始GSA算法的初始种群是随机分布的,其覆盖空间具有很大的不确定性,本文采用网格算法初始化质点的位置群,使初始个体在海域中均匀分布,其表达式如式(6)所示:
(6)

利用网格初始化种群,可以在保证初始变量随机性的前提下,提高种群的遍历性,使算法遍历所有可能的状态,有利于克服一般随机初始化种群给优化算法搜索带来的局限性。
3.2 基于适应度值的自适应权值
为进一步提高GSA算法的优化性能,避免在复杂高维多模函数优化中出现的早熟现象,提出了线性递减权值策略。虽然它在一定程度上有利于改善优化性能,但算法没有考虑到优化问题的适应度值,在处理部分复杂非线性优化问题时将有可能降低优化性能。因此,本文在线性递减惯性权值的基础上结合适应度提出自适应递减的惯性权值位置更新策略:
(7)
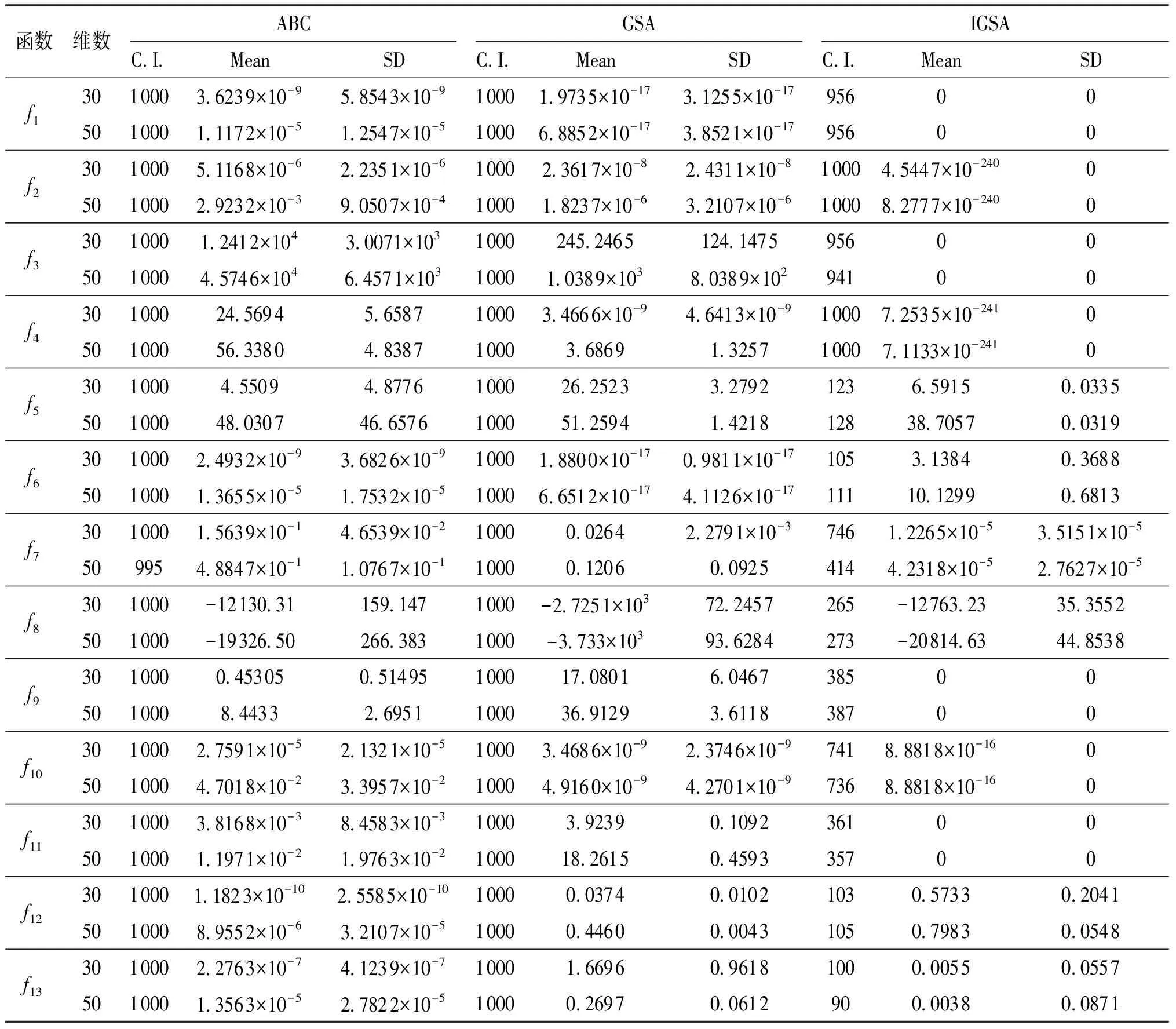
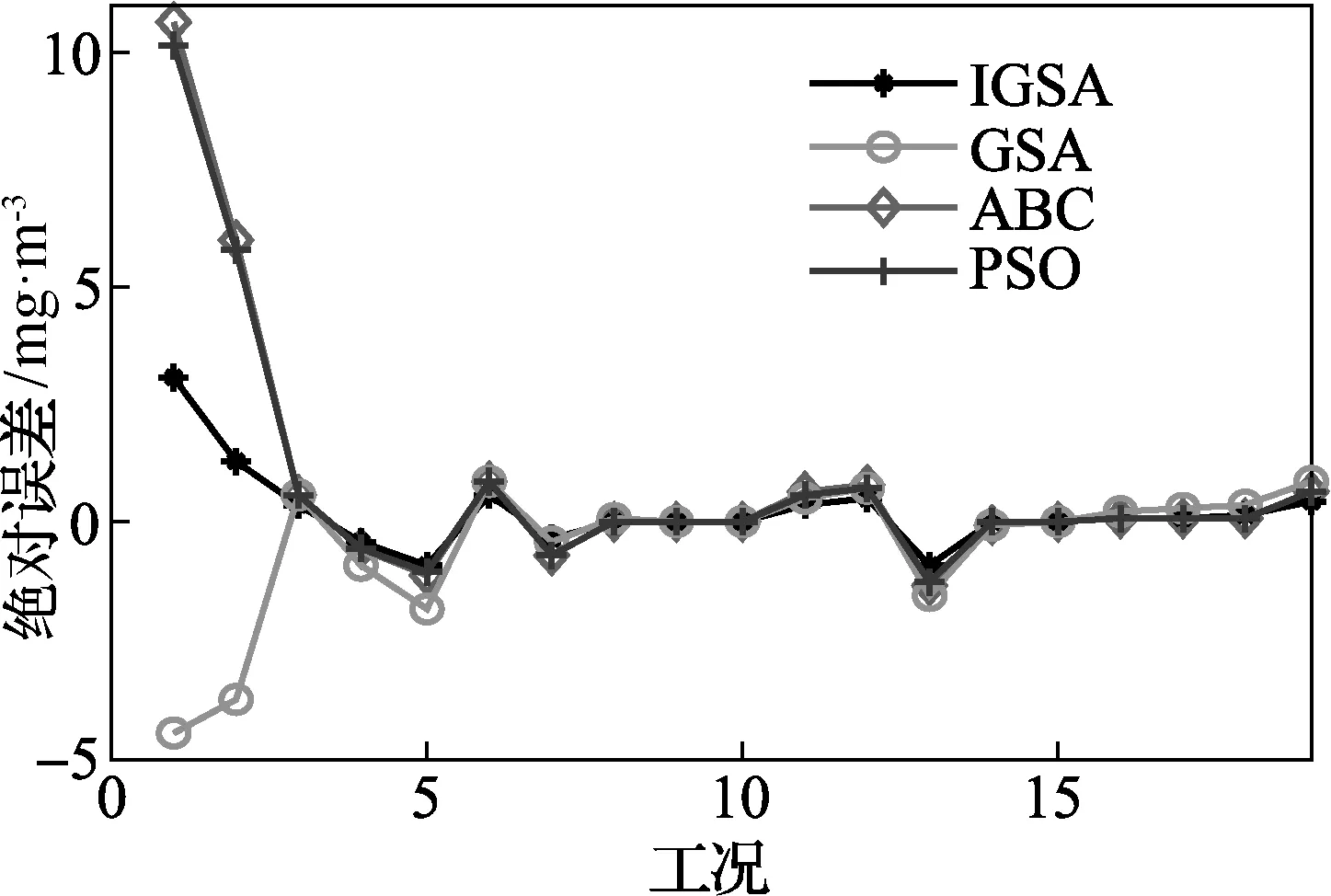
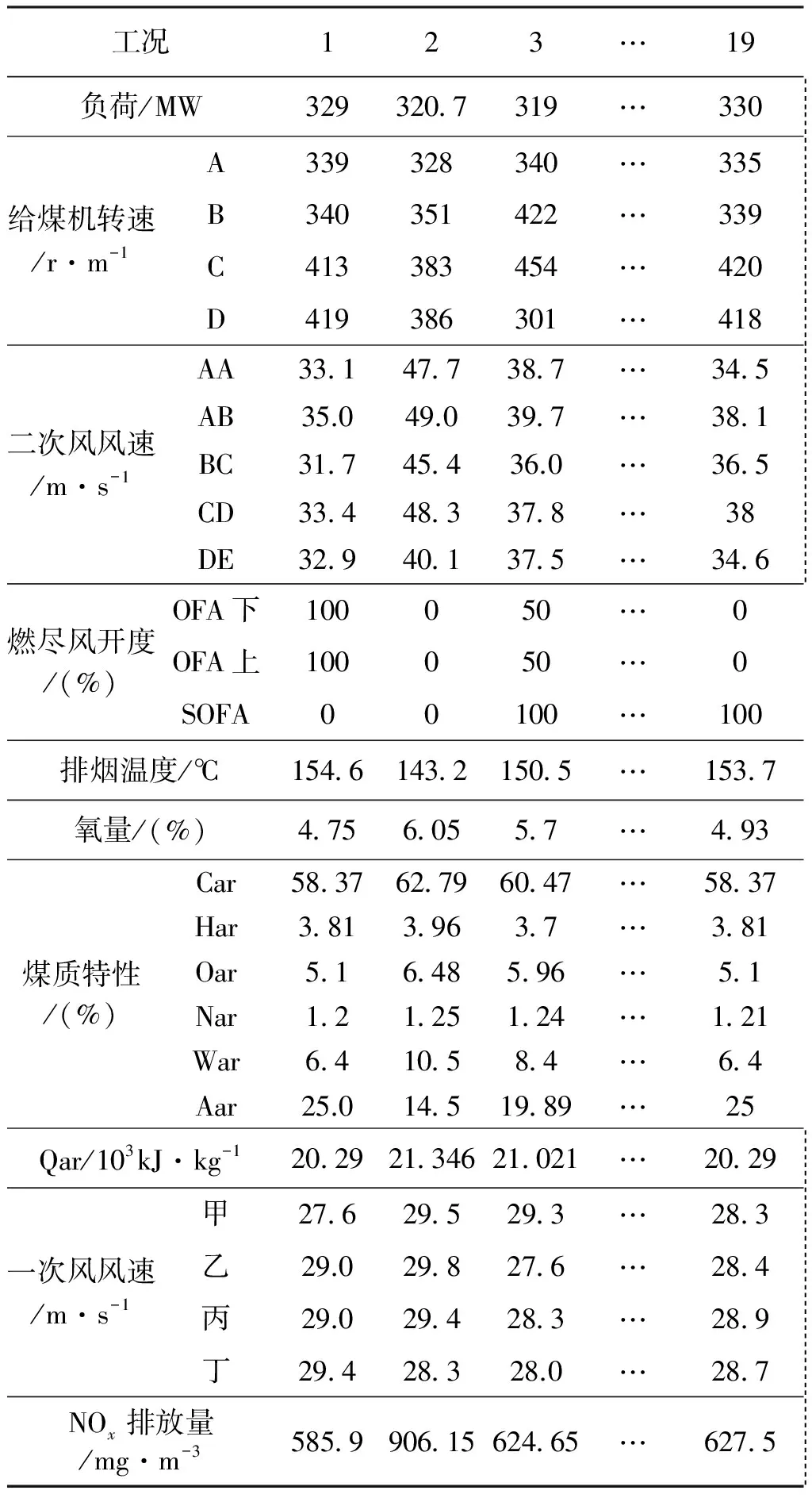
式中:ts和te分别为初始值和最终值,且0 将式(7)代入式(5),得到质点的位置更新: (8) (1)初始化参数:最大迭代次数imax=1 000,种群数N=50; (2)网格算法初始化种群; (3)计算种群质点的适应度值; (4)更新数据G(t),Ab(t),Aw(t)和Mi,i=1,2,…,N; (5)按式(3)更新质点在各个方向上的合力; (6)按式(5)计算质点的速度; (7)按式(7)、式(8)更新质点的位置,ts和te分别设为1和0; (8)重复步骤(3)~(7),直到停止条件满足。 选取13个标准函数用来评价IGSA的优化性能,f1~f7为单模态函数,只有一个极值点,主要用来考察算法的执行能力并测试算法的寻优精度;f8~f13为多模态函数,具有大量的局部最优点,是优化领域中公认的较难优化的函数,大部分优化算法在对其进行寻优的过程中往往会陷入局部最优点,主要用来检验算法是否具备避免早熟并搜索全局最优解的能力。除f8的最小值为-418.982 9×n(n为解的维数)外,其它12个函数的最小值均为零。文献[11]描述了标准函数解的取值范围,指出原始GSA优于PSO、RGA和CFO。本文进行了蜂群算法(ABC)与原GSA以及IGSA的对比,结果见表1。 为有效减少随机干扰的影响,每个算法均独立运行30次。表中,C.I.为平均收敛迭代次数,Mean为平均最优适应度值,SD为标准差。 分析表1给出的13个标准测试函数的优化结果发现:对于单模态函数,除f6外,在3种算法中,无论函数为30维是50维,IGSA的优化效果均为最好的,且优势明显;对于多模态函数,除f12外,IGSA的优化效果均为最好的。因而相对于ABC和GSA,IGSA的优解的精度最高。同时还发现:当n=50,IGSA的优化精度基本上接近n=30的精度,这在某种程度上说明,随着问题复杂程度的增加,IGSA的优化效果并没有得到减弱;相比较而言,ABC和GSA随着维数的增加,绝大部分的优化效果都呈现下降趋势,尤其是ABC算法,随着问题复杂程度的增加,其优化能力下降明显。 标准差反映了算法的稳健性,平均函数收敛次数C.I.反映算法的计算收敛速度。由表1可知,ABC和GSA对13个标准函数不能一直精确地求解,相对来说,GSA优化性能较ABC稳定,同时可明显观察到IGSA的优化性能较ABC和GSA更精确,其跳出局部极值的能力也较强;在优化速度方面,IGSA的C.I.指标比另外2种算法要少;从标准差可看出ABC和GSA在求解单峰和多峰连续函数时数值计算不稳定,相比之下,IGSA是最稳定的。 最小二乘支持向量机(LSSVM)是SVM的改进且优势明显:(1)用等式约束代替SVM算法中的不等式约束;(2)将求解二次规划问题转化为直接求解线性方程组。两优点使LSSVM方法的优化问题的求解变为通过Kuhn-Tucker条件下得到的一组线性方程组的求解,在一定程度上降低了求解难度、提高了求解速度、改善了模型的泛化能力和预测精度,使之更能适应于现场实际应用。LSSVM目标函数定义为下: (9) s.t.yi-(wφ(xi)+b)=ξi,i=1,2,…,N (10) y(x) =wT·φ(x)+b (11) 表1 3种优化算法性能比较 基于RBF核的LSSVM建立煤粉锅炉NOx排放预测模型,模型性能主要由正则化参数C和核宽度δ决定[12]。由LSSVM的基本理论及算法推导过程可知,正则化参数和核参数对于建立有效的LSSVM预测模型至关重要。正则化参数在于调节置信范围和经验风险的比例,若选择的正则化参数值越大,意味着对LSSVM训练的误差惩罚也越大,此时训练数据的样本点和真实值的拟合会越好,但容易使模型陷入“过拟合”;若减小其值则会降低模型的复杂性。核参数主要影响样本数据在高维特征空间中的分布复杂程度,其值选择的越大,则模型的复杂度越小,也容易出现“过拟合”现象;核参数值越小,则模型拟合出的曲线越光滑。事实上,最小二乘支持向量机的超参数调整过程也是参数优化的过程,采用群智能优化算法优化选择超参数是LSSVM模型目前常用的参数选择方法。本文采用IGSA算法优化选择LSSVM参数对(C,δ2)。 在模型参数优化过程中,定义适应度函数: (12) 式中:Hr为实际值;Hp为模型的预测值。 图1为采用IGSA算法优化LSSVM参数、建立NOx排放模型的流程图。主要思路:采用IGSA算法对LSSVM模型的超参数进行优化,以目标函数适应度值最小为原则,通过判断是否满足终止条件,将优化得到的参数代入LSSVM模型,即完成IGSA-LSSVM模型的建立;利用得到的NOx排放模型分析、处理未来数据,从而有效地得到研究对象的估计或预测结论以便做出有价值的决策。 图1 IGSA-LSSVM预测模型流程图Fig.1 Flowchart for IGSA-LSSVM prediction model 采用IGSA算法优化LSSVM模型参数,预测某330 MW煤粉汽包锅炉NOx浓度排放量,预测结果与标准GSA、蜂群算法(ABC)和粒子群算法(PSO)优化方法进行比较。在NOx排放量多工况测试中,包含影响锅炉燃烧特性的各种运行参数,如发电负荷、给煤机转速、一次风、二次风等特性参数,具体数据见表2。 采用IGSA优化LSSVM中的惩罚系数C和核函数参数δ2,利用优化后的LSSVM模型预测NOx排放量。利用IGSA优化LSSVR模型参数,设定IGSA种群规模为50,在表2中的19组工况中,选取3~17组数据进行训练优化建模,1组、2组作为预测数据,以此验证IGSA的优化性能。 图2 4种算法预测值与实测值之间的误差曲线Fig.2 Error curve between prediction values and true values of 4 algorithms IGSA获得的最优模型参数(C,δ2)的值为(650, 175),利用此组参数对1组、 2组预测数据和另17组训练数据进行回归预测,同时与另外3种方法的综合建模进行实验对比,预测误差见图2。表3为4种预测方法预测NOx排放量的相对误差RE。由图2和表3可以看出:利用IGSA优化LSSVM模型参数,然后基于优化参数建立模型的预测精度较ABC、PSO、GSA优化模型的预测精度更高,即IGSA能够比ABC、PSO和GSA找到更好的模型参数。 表2 锅炉运行试验数据 表3 4种算法预测结果精度分析 燃煤锅炉NOx排放量特性受到多种因素的影响,且其影响关系复杂,NOx排放量的预测和控制均很困难,本文采用最小二乘支持向量机方法建立NOx排放量软测量模型。为改善LSSVM的预测精度和泛化能力,采用改进的引力搜索算法优化选择LSSVM的模型参数。以某电厂330 MW煤粉锅炉为测试对象,采用IGSA算法优化最小二乘支持向量机的超参数并建立NOx排放的预测模型,通过将DCS采集到的相关数据作为训练样本、测试样本,对模型进行训练和检验,仿真实验表明,基于IGSA-LSSVM的NOx排放预测模型有较好的准确性和较强的泛化能力。 [参考文献] [1] Tan P, Xia J. Modeling and optimization of NOxemission in a coal-fired power plant using advanced machine learning methods [J].EnergyProcedia,2014,61:377-380. [2] 牛培峰, 马云鹏, 张京.基于相关向量机的电站锅炉NOx燃烧优化[J].计量学报, 2016, 37(2): 191-196. Niu P F, Ma Y P, Zhang J. Utility boilers NOxcombustion optimization based on relevance vector machine[J].ActaMetrologicaSinica, 2016, 37(2): 191-196. [3] 牛培峰, 王丘亚, 马云鹏,等. 基于量子自适应鸟群算法的锅炉NOx排放特性研究[J]. 计量学报, 2017, 38(6): 770-775. Niu P F, Wang Q Y, Ma Y P,etal. Study on NOxemission from boiler based on quantum adaptation bird swarm algorithm[J].ActaMetrologicaSinica, 2017, 38(6): 770-775. [4] 张维平, 赵文蕾, 牛培峰.基于粗糙集与最小二乘支持向量回归的汽轮机主蒸汽流量预测[J].计量学报, 2015, 36(1): 43-47. Zhang W P, Zhao W L, Niu P F. Forecasting of turbine main steam flow based on rough sets and least squars support vector machine regression [J].ActaMetrologicaSinica, 2015, 36(1): 43-47. [5] Liu C, Niu P F. A hybrid heat rate forecasting model using optimized LSSVM based on improved GSA[J].NeuralProcessingLetters,2017,45:299-318. [6] Li Q, Niu P F, Zhang W P. Model NOxemissions by least squares support vector machine with tuning based on ameliorated teaching-learning-based optimization [J].ChemometricsandIntelligentLaboratorySystems,2013,126:11-20. [7] 牛培峰, 王培坤, 李国强.基于自由搜索算法和支持向量机的燃煤锅炉NOx建模与优化[J].计量学报, 2014, 35(6): 626-630. Niu P F, Wang P K, Li G Q. Modeling and optimization of NOxfor coal-fired boilers by free search algorithm and support vector machine [J].ActaMetrologicaSinica, 2014, 35(6): 626-630. [8] Esmat Rashedi, Hossein Nezanudmdi-pour, Saryazdi Saryazdi. GSA: A Gravitational Search Algorithm[J].InformationSciences,2009,179(13):2232-2248. [9] Gouthamkumar N, Sharma Veena, Naresh R. Disruption based gravitational search algorithm for short term hydrothermal scheduling[J].ExpertSystemswithApplications,2015,42(20):7000-7011. [10] Sajjad Yazdani, Hossein Nezamabadi-pour, Shima Kamyab. A gravitational search algorithm for multimodal optimization[J].SwarmandEvolutionaryComputation,2014,14:1-14. [11] Li G Q, Niu P F, Xiao X J. Development and investigation of efficient artificial bee colony algorithm for numerical function optimization[J].AppliedSoftComputing, 2012, 12(1): 320-332. [12] 牛培峰, 刘超, 李国强.汽轮机热耗率多模型建模方法研究[J].计量学报, 2015, 36(3): 251-255. Niu P F, Liu C, Li G Q. Investigation on multi-model modeling method of steam turbine heat rate[J].ActaMetrologicaSinica, 2015, 36(3): 251-255.
3.3 IGSA优化步骤
3.4 IGSA性能验证
4 NOx排放预测模型
4.1 最小二乘支持向量机

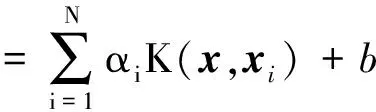
4.2 IGSA优化的LSSVM模型
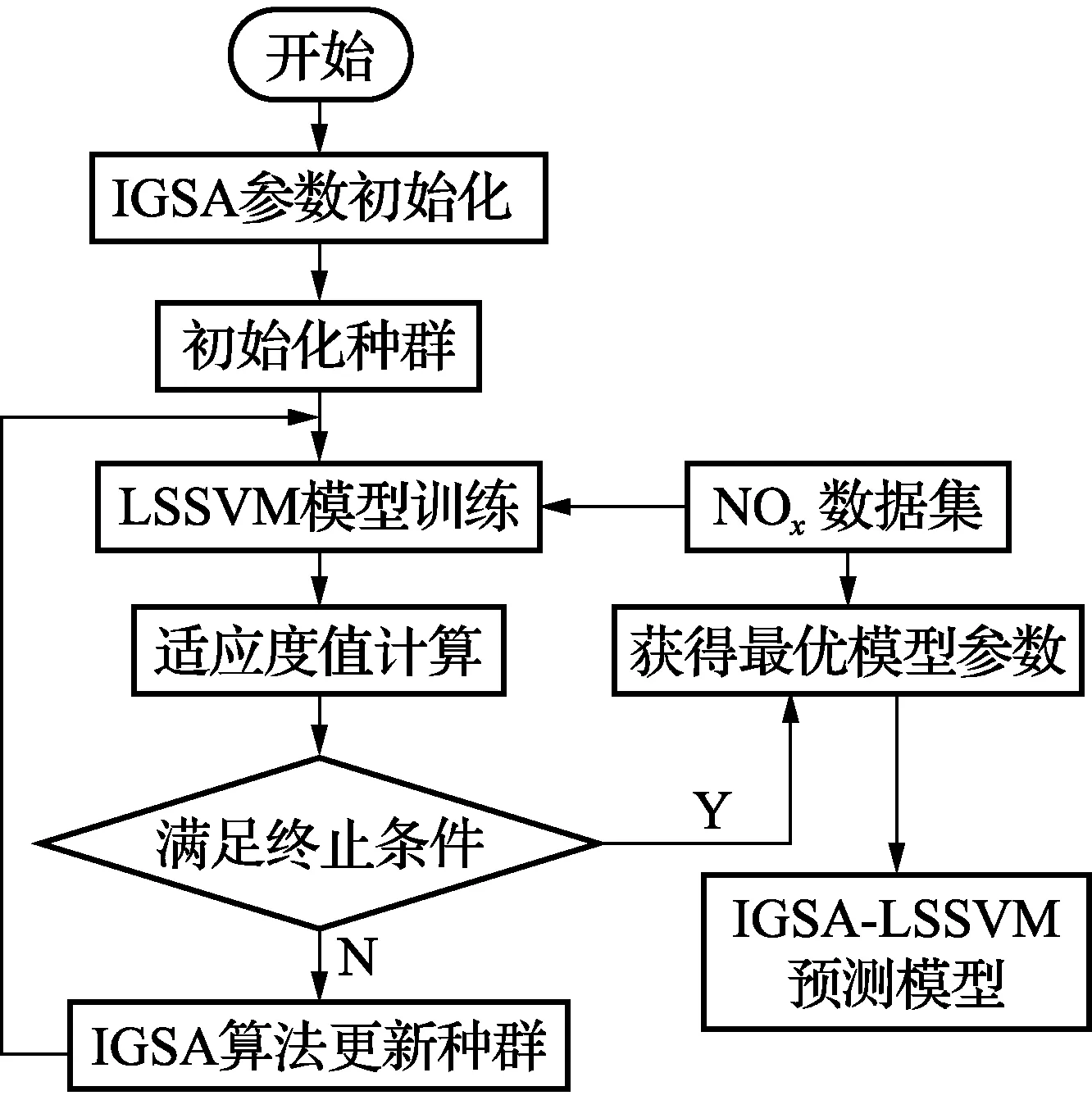
4.3 IGSA-LSSVM预测NOx排放量

5 结 论
