游标类量具检定装置的驱动系统误差补偿
2018-06-22陈旺达徐志玲厉志飞中国计量大学浙江杭州3008杭州市质量技术监督检测院浙江杭州3009
陈旺达, 徐志玲, 厉志飞(. 中国计量大学, 浙江 杭州 3008; . 杭州市质量技术监督检测院, 浙江 杭州 3009)
1 引 言
游标类量具是制造业最常用的高精度量具之一,在工程测量中普遍使用,比如游标卡尺。然而,目前对于高精度的游标类量具的检定仍然还停留在实验室人工检定阶段,检定效率低、检定结果易受检定人员情况的影响。
游标类量具检定时,需要将量具上的游标移动到指定的待检点位置。游标的移动主要是利用滚珠丝杠直线导轨和动态工作台,移动过程中速度从加速到匀速到最后减速,当接近指定的待检点时,动态工作台减速。由于游标卡尺各检定点相距较近,移动的平均速度为5 mm/s,属于低速运动[1]。当处于低速运动时,动态工作台与导轨表面存在摩擦力,驱动系统会受到非线性摩擦的影响[2]。如果采用复杂的摩擦模型消除此非线性影响[3~5],需要十分精确的摩擦参数。常用的高精度摩擦模型有LuGre和Maxwell模型等。向红标等人[6]利用LuGre摩擦模型,设计了开放式的伺服系统的动力学模型,最后采用Backstepping方法设计自适应摩擦补偿控制器,在实验中输入正弦信号,验证了该补偿方案能有效减小由摩擦所带来的影响,降低了其跟踪误差;周金柱等人参考LuGre模型,构造非线性观测器来估计摩擦力矩[7],采用积分反步自适应控制算法[5],实现摩擦补偿和负载扰动估计,其仿真结果也表明LuGre摩擦会对低速运动产生影响,而提出的补偿方法能够降低摩擦所带来的影响,并提高系统的跟踪精度和鲁棒性。
检定装置驱动系统中的螺杆与螺母间的齿隙非线性会导致控制系统的时滞、振荡等问题的产生[2]。对于齿隙补偿,已经开发了几种控制方案[8~10],但在滚珠丝杠驱动的线性运动阶段,如果没有配备一个特殊的力传感器[11],很难预测螺母驱动力及建立齿隙输入和输出非线性的数学关系。
由于在任何精度条件下,神经网络均可以建立相应非线性动力学模型[3],本文采用LuGre摩擦模型和自适应律周期性的递归小波神经网络(recurrent wavelet neural networks,RWNNS),以补偿滚珠丝杠驱动的摩擦和齿隙非线性误差。LuGre摩擦模型可以全方位描述摩擦力现象[12],消除由动态工作台与导轨间摩擦所引起的各种误差;RWNNS利用母小波层的时间反馈完成复杂的非线性动力学模型的研究[13,14]。图1为RWNNS示意图。
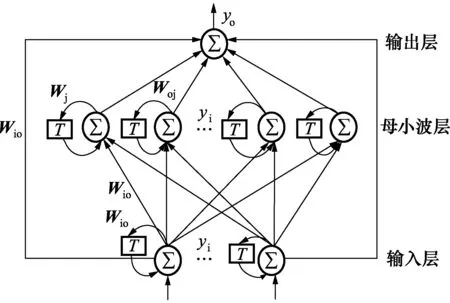
图1 RWNNS 示意图Fig.1 Diagram of RWNNS
2 驱动系统结构设计与分析
游标类量具的自动检定装置是基于机器视觉的检定装置,由机械模块、机电控制模块和视觉检测模块构成的机电一体化结构。标准光栅尺作为检定装置的标准值,放置于游标类量具的运动延长线上,消除了阿贝误差。在检定过程中,检定装置带动游标卡尺移动,到达检定规程中所要求的检测点,高精度光栅尺可以实时测量当前移动的距离。光栅尺测得的距离作为标准值,代替了传统量块的功能;装置的视觉检测系统完成刻度面的读数任务,并与标准数值进行比较,判断游标类量具示值面的准确性。因此,游标卡尺定位的准确性影响装置的检测结果的准确性。
游标的移动是依靠机电控制模块中的驱动系统实现。驱动系统包括滚珠丝杠直线导轨和动态工作台。游标固定在动态工作台上,动态工作台在滚珠丝杠上运动,当动态工作台带动游标移动,将要达到指定点时,工作台处于低速运动阶段,此时由于工作台与导轨表面间受到摩擦力的影响,会产生粘滑、稳态不平稳等一系列误差[2,15],而这些低速运动阶段的非线性摩擦往往会影响装置的定位精度及后续的检定工作[16]。图2为游标类量具检定装置。

图2 游标类量具检定装置图Fig.2 Calibration device for vernier measuring tools
3 低速状态下驱动系统的误差分析
当驱动系统中的动态工作台处于低速运动阶段,会受到非线性误差的影响,非线性误差包括摩擦和齿隙误差。图3为检定装置驱动系统的结构示意图。驱动系统由步进电机提供动力,将电机的旋转运动等效为同步化的线性运动[17]。等效动力学方程式[6]为
(1)
式中:m为总质量;x为动态工作台位移量;σ2为粘滞摩擦系数;Ff为一个等效非线性摩擦力;Fu为模型误差、静态负载及外部干扰因素的总和;w(v)为非线性齿隙输入函数,v为输入控制。
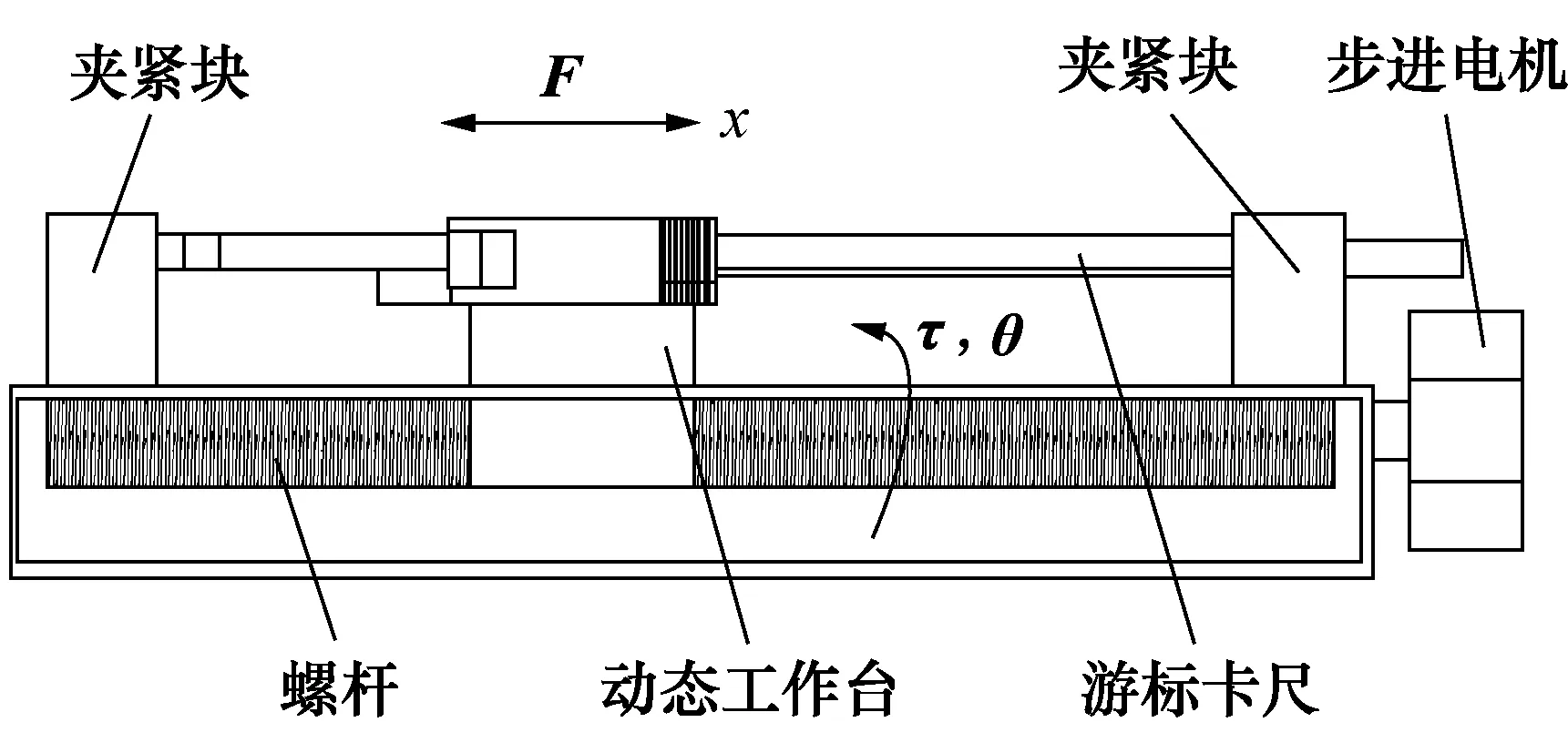
图3 检定装置驱动系统的结构示意图Fig.3 Structure diagram of driving system of calibration device
图4为正弦波输入的位置响应实验结果,由图4的响应结果可以看出,实验结果呈非线性关系,非线性齿隙函数难以用固定的数学模型来求解;但从图中可以发现,非线性输入控制函数依然能够用公式(2)[7]来表示
w(v)=cv+fb(v)
(2)
式中:c>0为该直线的斜率;fb(v)表示未知齿隙非线性函数。
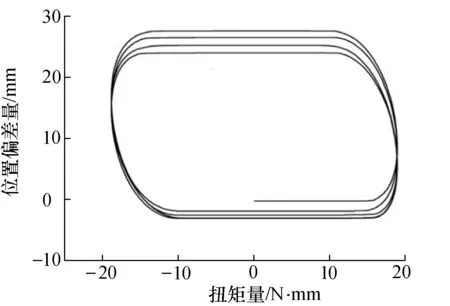
图4 正弦波输入的位置响应实验结果Fig.4 Experimental results of position response of sinusoidal wave input
利用LuGre摩擦模型[7],可以得到
(3)


(4)
记变量x1=x,x2=x1,c=1,则
(5)
式中:gp=1/m;db=gpfb;Fd=gpFu。
4 齿隙及摩擦补偿

(6)
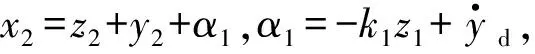
(7)
根据Yough的不平衡性定律[18],得
(8)
记过滤模拟控制器参数λ2,α1通过一阶滤波器后得到的时间常数为τ2,设τ2λ2+λ2=α1,λ2(0)=α1(0),y2=λ2-α1,可得
(9)
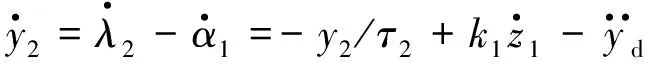
(10)

(11)

(12)
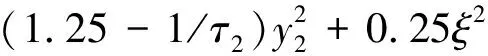
(13)
同理[15],可得

(14)
式中:z2=x2-λ2。
综上所述,在新课程改革不断深入的背景下,新时期我国在积极加强小学生人才培养的过程中,要求小学语文教师充分发挥学科优势,在积极进行教材挖掘的基础上,从传统文化素养以及综合素质等角度出发,采取有效措施不断促进小学生身心健康发展。因此,新时期,小学语文教师应对学生传统文化素养培养的重要性产生深刻认知,并从注重培养学生对传统文化的情感基础、通过传统文化传承培养小学生语文核心素养、结合教学内容深入挖掘传统文化精华等角度出发,为促进小学生传统文化素养的提升奠定基础。
为保证db的最优化,记RWNNS[13,14]公式为
(15)
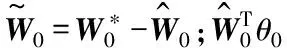
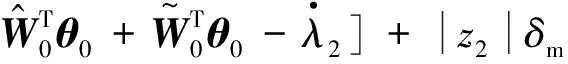
(16)
若满足|δ|≤δm,δm为正数,引入z2=x2-λ2,滑动面的误差变量为
(17)
滑动面定义的简单化有利于较容易地应用到控制器中,选择一个控制输入量[14]
(18)
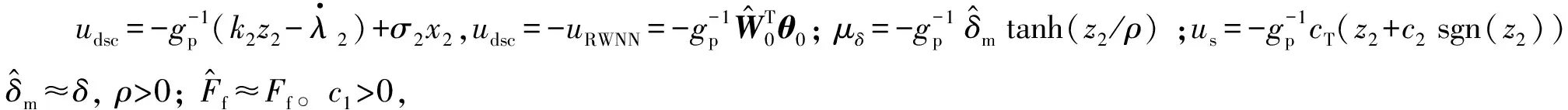
0≤|z2|-z2tanh(z2/ρ)≤0.2785ρ
(19)
将式(18)和式(19)代入式(16),得齿隙非线性的补偿估计值为
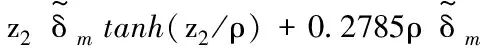
(20)
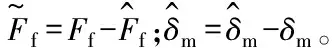
由于LuGre摩擦模型预滑动区域的局限性[12],故通过摩擦状态观测器的值来对z进行估计
(21)
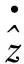
(22)

(23)
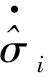
(24)

(25)
5 模型的建立与仿真分析
为探究自适应律的递归小波神经网络(RWNNS)和LuGre摩擦模型对摩擦与齿隙的非线性误差的补偿效果,设计了4个控制器来评价控制系统的性能:动态表面控制器(DSC系统)、滑模控制动态表面控制器(DSC_S系统)、滑模控制和摩擦估计动态表面控制器(DSC_SF系统)以及滑模控制、摩擦估计和动态表面控制器(DSC_SFWN系统)。选择正弦信号作为位置输入指令,对仿真结果进行分析。
为保证仿真结果的准确性和直观性,建立了如图5所示的DSC_SFWN控制系统,通过输入正弦位置指令来确定输出的模拟结果,见图6,其中图6(a)为位置跟踪性能,图6(b)为跟踪误差。
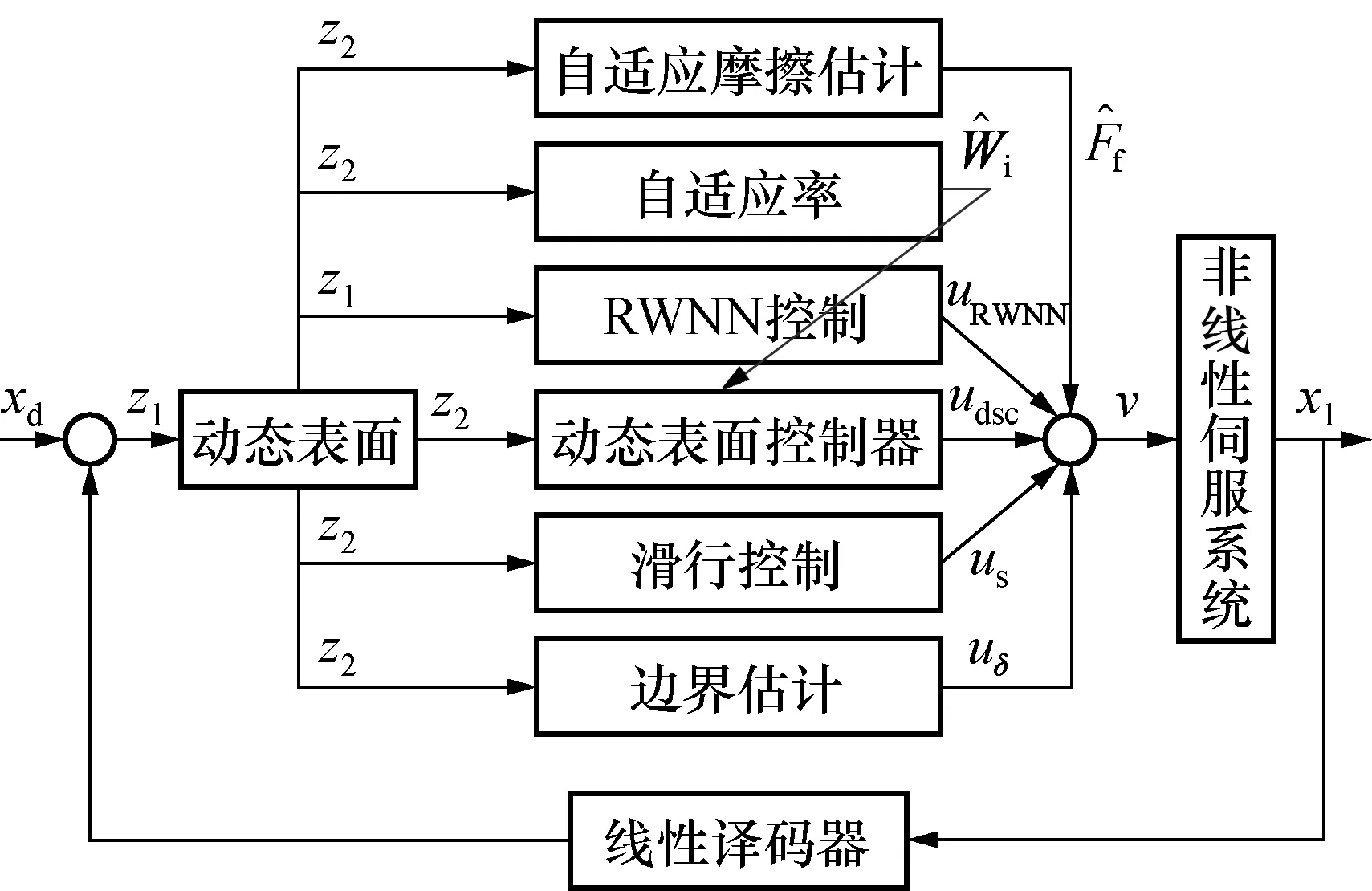
图5 DSC_SFWN控制系统框架Fig.5 Block diagram of DSC_SFWN control system

图6 正弦波位置指令输入的模拟结果Fig.6 Simulation results of sinusoidal position instruction input
仿真结果见表1。驱动系统的均方根误差包括绝对值和相对值,其中相对值计算是通过其他3个控制器的值分别除以动态表面控制器(DSC系统)对应的数值而得。

表1 仿真中各控制系统的均方根误差Table 1 Root mean square error of control system in simulation
由于摩擦和齿隙非线性误差的存在,在未进行误差补偿前,驱动系统位置跟踪性能差,但由表1中的均方根误差数值可以得出,在经过摩擦和齿隙非线性误差的补偿后,位置跟踪性能得到了极大的改进。因此,通过仿真结果的验证,所提出的控制方案在性能方面比传统方案要更加优越,适用于补偿驱动控制系统在驱动时因受摩擦和齿隙非线性影响而产生的误差,同时从数据结果中可以发现该控制方法具有高效性、适用性和实用性的特点,值得推广。
6 补偿模型驱动系统中的验证
非线性补偿模型在仿真中得到了验证,其控制方案比传统控制方案更加优越,对摩擦和齿隙非线性的补偿更显著。现将该控制补偿方案应用到装置的驱动系统中,驱动系统控制游标类量具(以游标卡尺为例)移动到检定规程中必检点。高精度光栅尺测量游标卡尺的实际移动距离,作为装置的标准数值,其测量精度高于待检游标卡尺的精度。由于游标卡尺的精度为0.02 mm,因此高精度光栅尺的精度需达到0.001 mm。记录正反行程中实际点数值,并与指定点数值进行对比,来判断补偿方案的合理性。表2、表3为游标卡尺在移动中正反行程中实际点与指定点的偏差。
从表中可以发现:在补偿前,正行程中最大的偏差值为0.035 mm,最小的偏差值为0.013 mm,平均偏差为0.021 mm;在反行程中最大的偏差值为0.035 mm,最小的偏差值为0.011 mm,平均偏差为0.023 mm;在补偿后游标卡尺在正反行程的移动中,尽管依然存在着一定的偏差值,但正行程中最大的偏差值为0.014 mm,最小的偏差值为0.008 mm,平均偏差为0.011 mm;在反行程中最大的偏差值为0.016 mm,最小的偏差值为0.008 mm,平均偏差为0.012 mm。从数值中可以看出,利用非线性补偿模型进行补偿后,存在的偏差数值依然没有达到理想的状态,准确度较低。但是这些偏差均在 0.013 mm 左右,精密度较高,可以在后续再次进行数值补偿后达到接受的范围之内。由此可以表明,经过装置的实验验证,驱动系统非线性补偿模型能够有效地补偿由摩擦和齿隙非线性所带来的误差。
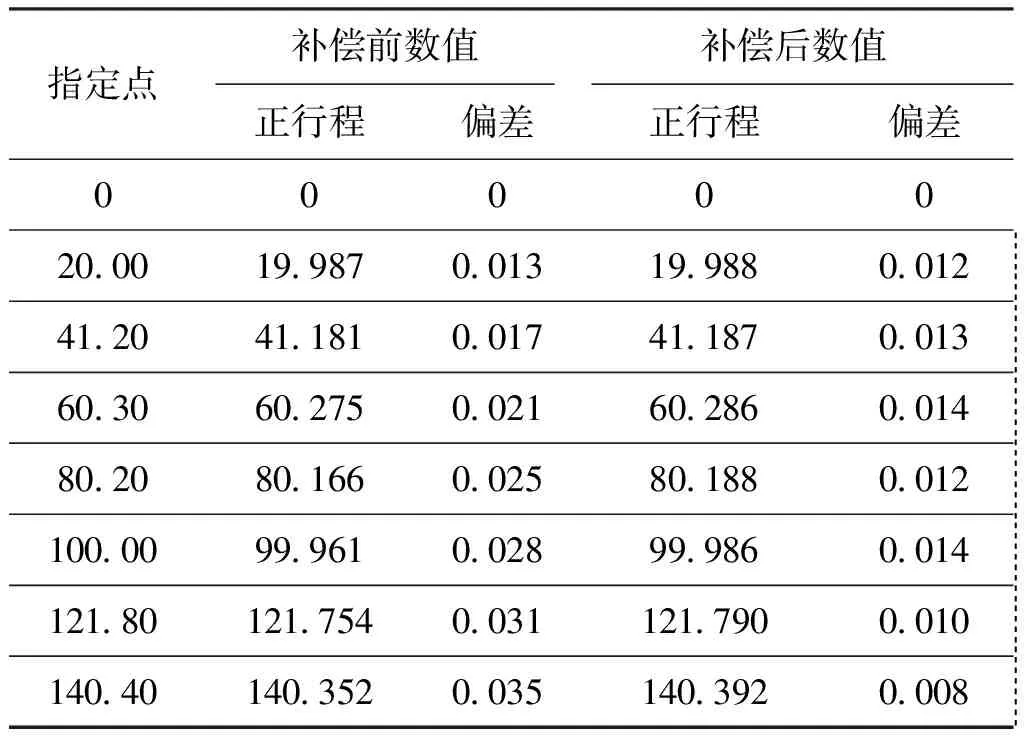
表2 正行程中实际点与指定点的偏差Table 2 Deviation between the actual point and the specified point in the positive movement mm
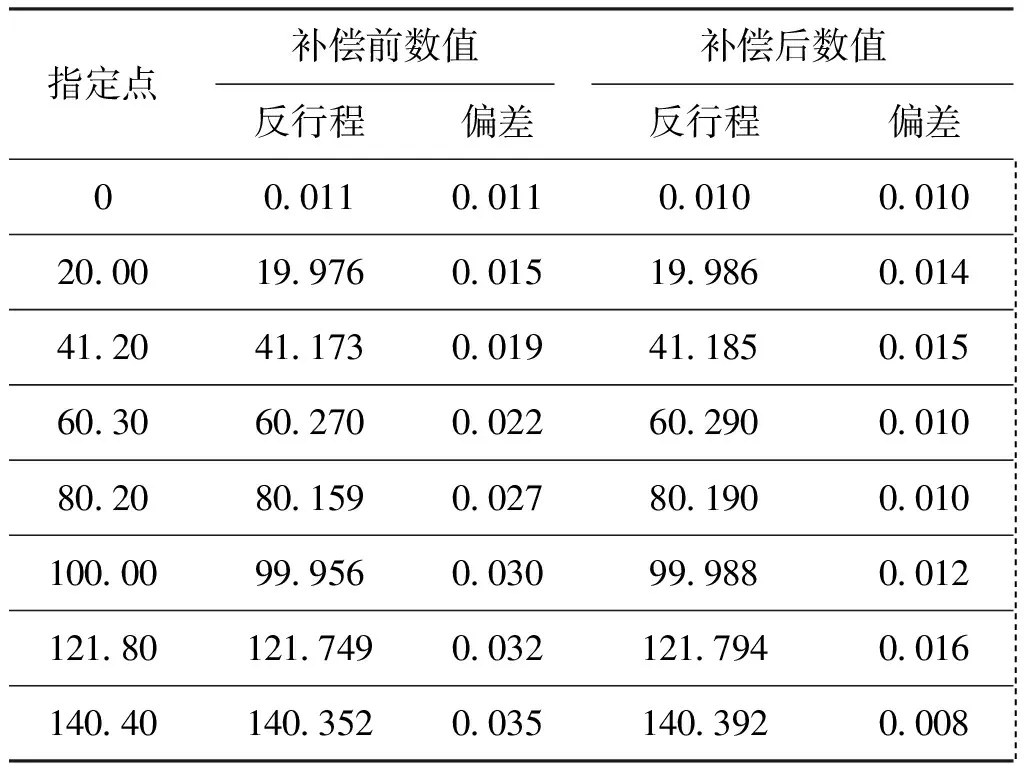
表3 反行程中实际点与指定点的偏差Table 3 Deviation between the actual point and the specified point in the negative movement mm
7 结 论
本文采用LuGre摩擦模型和周期性递归小波神经网络(RWNNS)方法补偿了摩擦与齿隙的非线性误差。结合仿真实验结果,证明该控制方法的有效性:不仅提高位置跟踪性能,增强位置跟踪动态面控制,而且有利于滚珠丝杆驱动系统的改进,减小系统运行误差,提高定位精度。将补偿方案应用到游标类量具检定装置的驱动系统中,装置的定位精度在正行程运动上平均提高了47.6%,反行程运动上平均提高了49.7%。
[参考文献]
[1] 刘丽兰,刘宏昭,吴子英.进给系统中速度爬行响应特征分析[J].机械设计,2017,34(6):17-22.
Liu L L,Liu H Z,Wu Z Y.Response characteristic analysis of stick-slip velocity in feed system[J].JournalofMachineDesign,2017,34(6):17-22.
[2] 赵国峰.一类齿隙非线性控制系统的研究[D].南京:南京理工大学,2005.
[3] 张鹏,李颖晖,肖蕾.基于递归神经网络的伺服系统自适应反步控制[J].系统仿真学报,2008,20(6):1475-1478.
Zhang P, Li Y H, Xiao L.Adaptive-backstepping control for servo system based on recurrent-neural-network[J].JournalofSystemSimulation,2008,20(6):1475-1478.
[4] 许颖,于化东,于占江,等.微小摩擦测试系统设计[J].计量学报,2013,34(5):452-456.
Xu Y, Yu H D, Yu Z J,etal.Design of the micro-friction testing system[J].ActaMetrologicaSinica,2013,34(5):452-456.
[5] 孙艳玲,常素萍.接触式表面轮廓测量的非线性误差分析与补偿[J].计量学报,2016,37(6): 563-566.
Sun Y L, Chan S P.Analysis and compensation of the nonlinear error based on contact surface profil measurement [J].ActaMetrologicaSinica,2016,37(6): 563-566.
[6] 向红标,谭文斌,李醒飞,等.基于LuGre模型的自适应摩擦补偿[J].机械工程学报,2012,48(17):70-74.
Xiang H B, Tan W B, Li X F,etal.Adaptive friction compensation based on LuGre model[J].JournalofMechanicalEngineering, 2012, 48(17): 70-74.
[7] 周金柱,段宝岩,黄进.LuGre摩擦模型对伺服系统的影响与补偿[J].控制理论与应用,2008,25(6):990-994.
Zhou J Z, Duan B Y, Huang J.Effect and compensation for servo systems using Lu Gre friction model[J].ControlTheory&Applications, 2008, 25(6):990-994.
[8] 王洪斌,周振,王跃灵,等.非线性系统的有限时间扩张状态观测器的设计[J].计量学报,2017,38(6): 725-729.
Wang H B, Zhou Z, Wang Y L,etal.Finite time extended state observer designed for nonlinear systems[J].ActaMetrologicaSinica, 2017,38(6): 725-729.
[9] 于占东,王庆超.一类不确定非线性系统反步自适应神经网络控制研究[J].控制与决策,2004,19(5):561-564,569.
Yu Z D, Wang Q C.Adaptive backstepping neural control for a class of uncertain nonlinear systems[J].ControlandDecision,2004,19(5): 561-564, 569.
[10] 黄俊朋.提高含齿隙伺服系统运动精度的控制研究[D].哈尔滨:哈尔滨工业大学,2010.
[11] 赵浩.一种自补偿差动式扭矩传感器的研究[J].计量学报,2016,37(4): 394-397.
Zhao H.Study on self compensating differential torque sensor[J].ActaMetrologicaSinica,2016,37(4): 394-397.
[12] 杨帆.基于LuGre摩擦模型的伺服系统自适应鲁棒控制研究[D].南京:南京理工大学,2012.
[13] Fang Y, Chow T W S, Li X D.Use of a recurrent neural network in discrete sliding-mode control[J].IEEProceedings-ControlTheoryandApplications,1999,146(1):84-99.
[14] Lin F J, Wai R J, Hong C M.Recurrent neural network control for LCC-resonant ultrasonic motor drive[J].IEEETransUltrasonFerroelectrFreqControl, 2000, 47(3): 737-49.
[15] 包达飞,汤文成,董亮.带摩擦补偿的滚珠丝杠副进给系统自适应滑模控制[J].东南大学学报(自然科学版),2015,45(3):455-460.
Bao D F, Tang W C, Dong L.Adaptive sliding mode control of ball screw drives with friction compensation[J].JournalofSoutheastUniversity(NaturalScienceEdition),2015,45(3):455-460.
[16] 马艳玲,黄进,张丹.伺服系统中齿隙非线性的自适应补偿[J].系统仿真学报,2009,21(5):1498-1504.
Ma Y L, Huang J, Zhang D.Adaptive Compensation of Backlash Nonlinearity for Servo Systems[J].JournalofSystemSimulation,2009,21(5):1498-1504.
[17] 周艳秋.步进电机定位控制技术的研究[D].大连:大连交通大学,2009.
[18] Yough K D.A variable structure control approach to friction force compensation[C]//American Control Conferenee, USA,Philadelphia ,1998:3138-3142.
