混合教与学算法在空间直线度评定中的应用
2018-06-22顾京君韦庆玥
杨 洋, 李 明, 顾京君, 王 宸, 韦庆玥
(上海大学 机电工程与自动化学院 智能制造及机器人重点实验室, 上海 200072)
1 引 言
根据相关几何误差评定标准[1,2],空间直线度的评定方法主要有两端点连线法,最小二乘法(least square method,LSM)和最小区域法,其中,前两种方法主要多应用于工程领域和三坐标测量机中,虽然算法相对简单易懂,但其评定结果并不精确,当所需精度较高时需要由最小区域法进行仲裁检验。而对于最小区域法,在相关标准中并没有规定具体的判定方法,只是给出了几何定义,因此,学者们对最小区域评定算法进行了深入的研究。
在最小区域算法的研究过程中,最小六面体包络法[3]、线性搜索算法[4]、线性规划[5]、计算几何[6]、凸壳理论[7]、半定规划[8,9]、网格搜索算法[10]和数据包络[11]等方法应用到空间直线度评定中。以上方法虽然都在一定程度上提高了空间直线度的评定精度,但存在求解过程复杂且容易陷入局部最优的问题,仍然难以满足最小区域原则。智能优化算法的不断发展,为解决此类高维复杂非线性问题的求解提供了很好的方法。其中,遗传算法(genetic algorithm,GA)[12]、粒子群算法(particle swarm optimization,PSO)[13]、人工免疫算法[14]和改进人工鱼群算法(least squares and artificial fish swarm algorithm,LA-AFSA)[15]等被应用到直线度误差评定过程,但是这些算法的计算结果与算法参数选择关系很大,算法的精度和鲁棒性仍可以继续提高。
本文将教与学优化算法[16](teaching learning based optimization,TLBO)应用到空间直线度误差评定中,该算法是一种新型的不依赖于参数选择的群体智能优化算法,其算法流程相对简单,控制参数少,而且收敛速度快,精度较高,已被广泛应用于工程优化领域[17,18]。同其他群智能优化算法的缺点一样,教与学算法在迭代后期收敛速度慢,容易陷入局部最优,因此为了进一步提高TLBO的后期求解能力,提出将混合蛙跳算法(shuffled frog leaping algorithm,SFLA)与教与学算法进行融合,设计了一种混合教与学算法(hybrid teaching-learning-based optimization,HTLBO),用以进一步提高空间直线度的求解精度。
2 HTLBO算法
TLBO算法是Rao R V在2012年提出的一种群体性智能优化算法,该算法控制参数很少,仅需设置种群规模、迭代次数、变量维度和控制变量上下限,通过模拟教师的教学与学生间的相互学习两个阶段从而达到寻优的目的,基本TLBO算法流程如文献[16]所述。对于基本TLBO算法,在教学过程中,班级中的所有学生向教师学习,学生成绩快速向教师靠拢,当迭代计算进行到后期时,导致种群多样性较低,使算法陷入局部最优[19],因此,借鉴SFLA的洗牌分组策略和局部更新策略[20,21],将其引入TLBO算法中,设计了一种HTLBO算法用以进一步提高教与学算法全局和局部搜索能力。
2.1 种群分组和洗牌策略
采用种群分组和洗牌策略的目的是增强学生间的信息交流能力,通过建立新的小组和各组的老师,从而增加算法的全局搜索能力,避免算法早熟。首先定义种群分组策略:确定班级里小组数目m,每组的学生人数n,从而确定产生初始学生数目为F(F=m×n),计算每个学生的适应度,将学生根据适应度按优劣进行排序,并记录下整个种群的适应度值最优的学生xt。按小组数目m将学生进行分组,划分准则是将排名第1的学生放入第1个小组,排名第2的学生放入第2个小组,第m的学生放入第m个小组,然后再将第m+1的学生放入第1个小组,以此类推,第2m的学生放入第m个小组,其中,第q个小组的学生Yq表达式为:Yq=x(q+m(p-1)),p=1,…,n;q=1,…,m)。同时记录全局最优学生xt和组内最优学生xt,m。
洗牌策略则是当每次迭代之后,将所有学生个体进行重新混合,按照上述方式进行重新排序、分组,进一步迭代计算,直到满足最大迭代次数或者达到计算精度为止。
2.2 局部更新策略
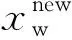
(1)
(2)
(3)
2.3 HTLBO算法步骤
HTLBO流程如下:
(1)参数初始化。设置初始化班级小组数目为m,小组学生数目为n,因此得到学生数量为F(F=m×n),问题的维度D,迭代次数W,变量上下限u、l,同时根据问题的不同建立目标函数的数学模型,输入实验数据,进入步骤(2)。
(2)教学阶段。按照2.1节所述的分组规则进行分组,通过教学公式进行教学更新,其中,教师为各组成绩最优者xt,m,并同时记录班级最优学员xt,组内成绩最差学员xw,进入步骤(3)。
(3)局部更新阶段。按照2.2节所述局部更新策略将最差学员xw再次进行更新,进入步骤(4)。
(4)学习阶段。按TLBO算法学习阶段进行计算,并更新每个学生的成绩,从而更新班级最优生xt的成绩和位置,进入步骤(5)。
(5)判断迭代过程或者计算精度是否满足要求,如果满足要求,则完成计算,此时,老师成绩的适应度值为所测数据点的空间直线度误差;如果没有,则通过洗牌策略重新进行分组,返回步骤(2)。
3 空间直线度的数学模型
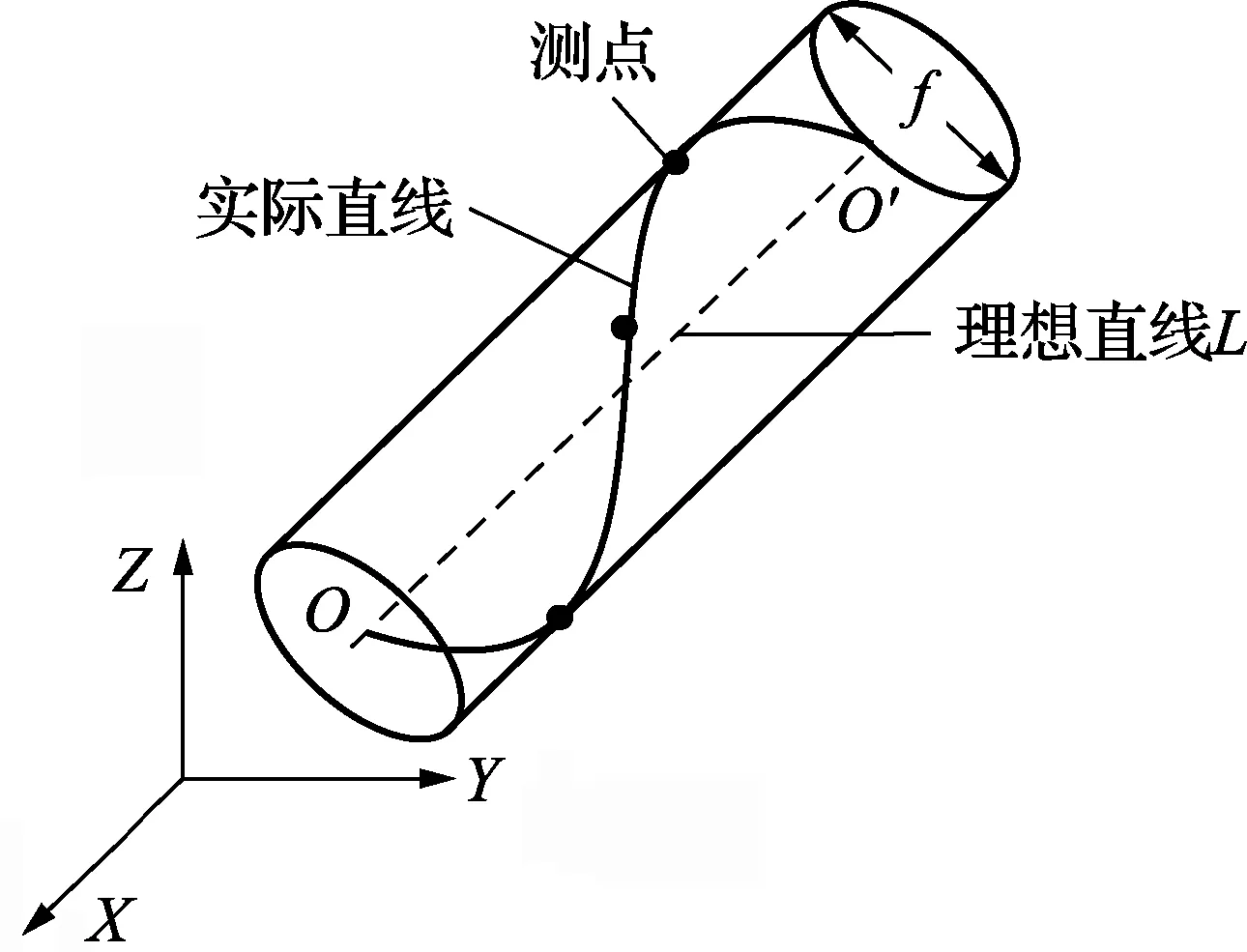
图1 空间直线度示意图
空间直线度误差本质上是实际直线相对理想直线的偏差量,体现的是包容所有测点的最小理想圆柱,如图1所示。因此,为了能够准确地计算出被测直线的空间直线度,首先通过空间直线的点向参数方程确立理想直线模型L,然后根据空间点到直线的距离公式,得到包容测点圆柱面里的最小圆柱半径,该半径的2倍(即圆柱直径)就是所求空间直线度误差,表达式如公式(4)所示[13]:
(4)
式中:(x0,y0,z0)为直线L上的某一定点;a,b,c分别为直线L在空间中X,Y,Z上的方向向量参数;i,j,k分别为三个坐标轴方向的单位向量;(xi,yi,zi)为测点集合;d为被测直线的空间直线度误差。
由直线度误差定义结合优化算法相关概念可知,实质上是求解未知参数(x0,y0,z0,a,b,c) 的问题,并且要满足最小区域条件(f最小),因此目标函数可以定义为公式(5)所示,即转化为极大值极小化问题。
f=F(x0,y0,z0,a,b,c)=min(maxd)
(5)
4 实验验证
4.1 空间直线度算例1
为了验证HTLBO算法的计算优越性,本次实验使用电脑操作系统为win7,处理器为I5- 4200ucpu@1.60 GHz 2.30 GHz,安装内存为4.00 GB,系统类型为64位,采用蔡司三坐标测量机UMC550S进行数据的获取,每6 mm选择一个截面,每个截面选取6个测点,采集试验零件的空间点坐标,进行空间直线度的分析,表1为被测要素圆心拟合坐标。
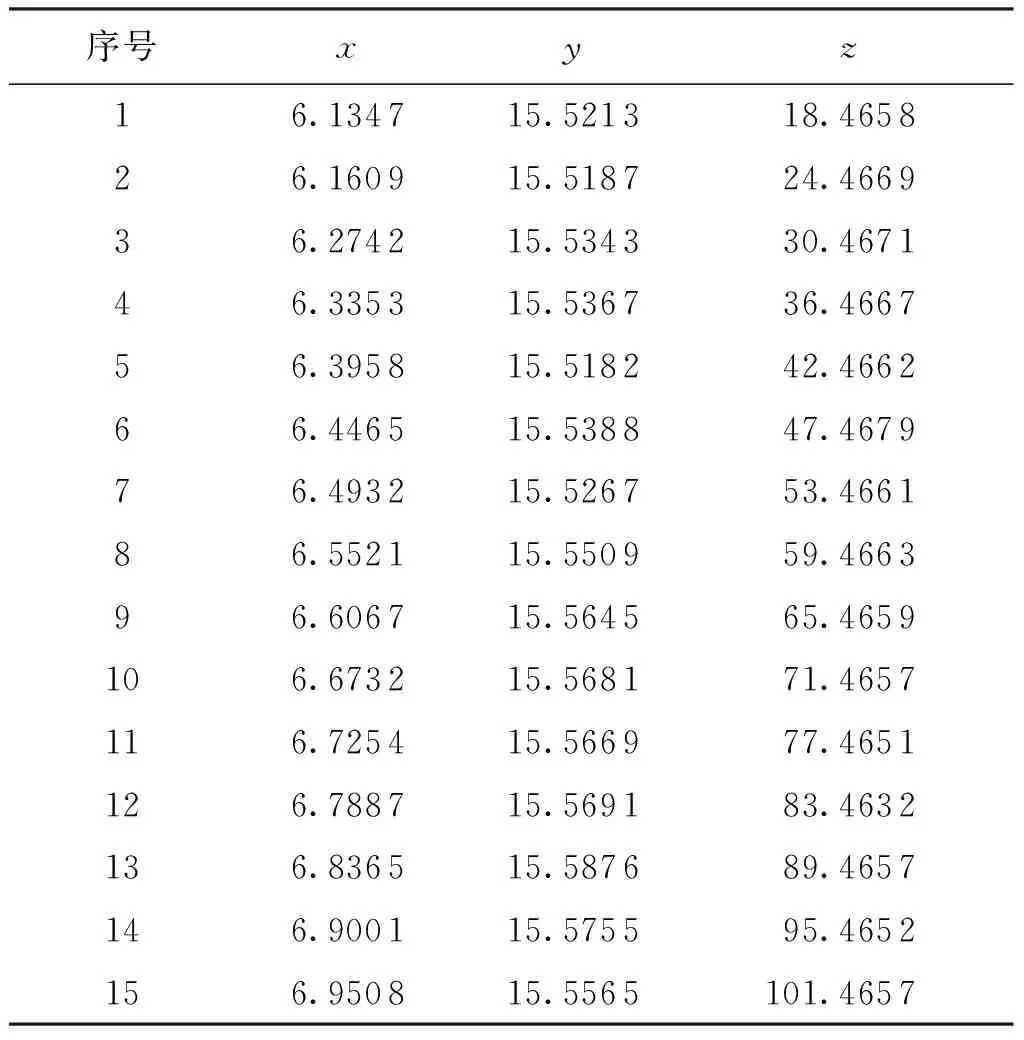
表1 被测要素圆心拟合坐标 mm
在程序参数上,设置小组数目为5,每组学生为10个,种群数目为50,维度为6,算法迭代次数为500次,运行次数为50次,求得平均误差。表2为不同的评定方法对应的直线度误差计算结果,对比计算结果可知, LSM计算的直线度误差为0.084 mm,其数值明显偏大,评定结果精度最低。在智能优化算法的评定结果中,HTLBO的计算结果与GA、PSO和TLBO算法相比,HTLBO算法求得的直线度误差最小,仅为0.063 2 mm。式(5)中各个参数的计算结果从表3可以得到,HTLBO求得的最小包容圆柱参数的中心轴线参数方程为F(x0,y0,z0,a,b,c)=F(5.730 6,15.498 2,-19.216 4,0.310 4,0.017 6,30.001 0) ,能够满足最小区域法对空间直线度的误差评定。图2为HTLBO、TLBO、GA、PSO等算法对表1数据进行直线度误差计算的迭代曲线,由于数据跨度较大且分布不均,因此采用对数刻度进行显示。从图2可以看到,在迭代计算过程中,HTLBO算法在迭代到96代时收敛,相对于其他3种智能优化算法收敛更快,收敛精度更高,体现了HTLBO算法在空间直线度的计算性能上的优势。
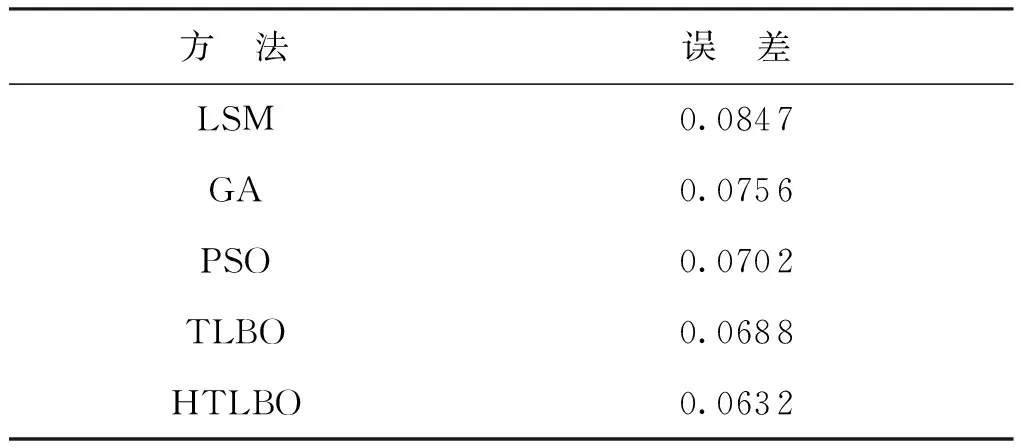
表2 直线度误差计算结果 mm
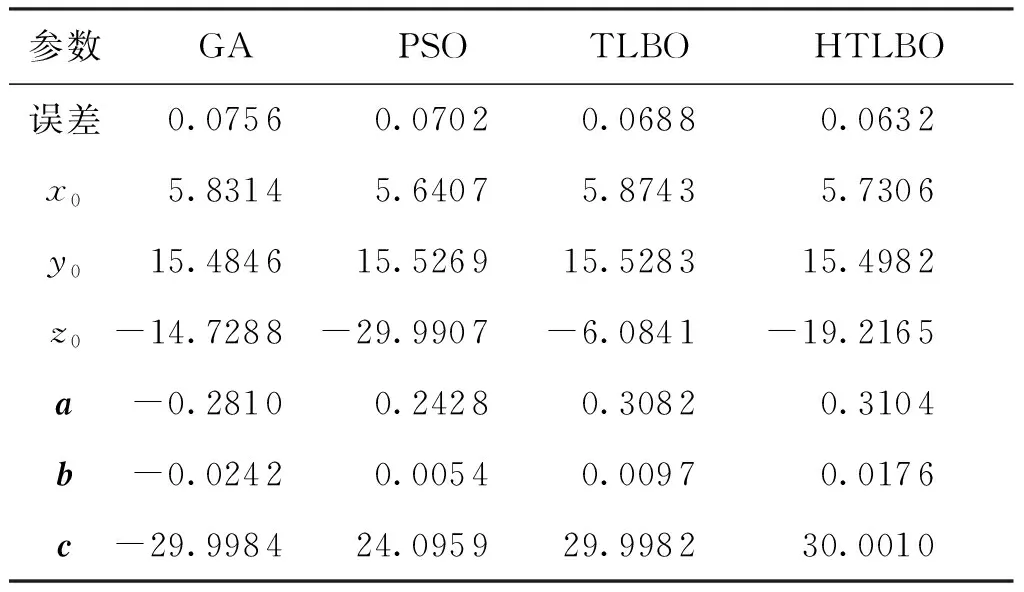
表3 4种算法参数的计算结果 mm
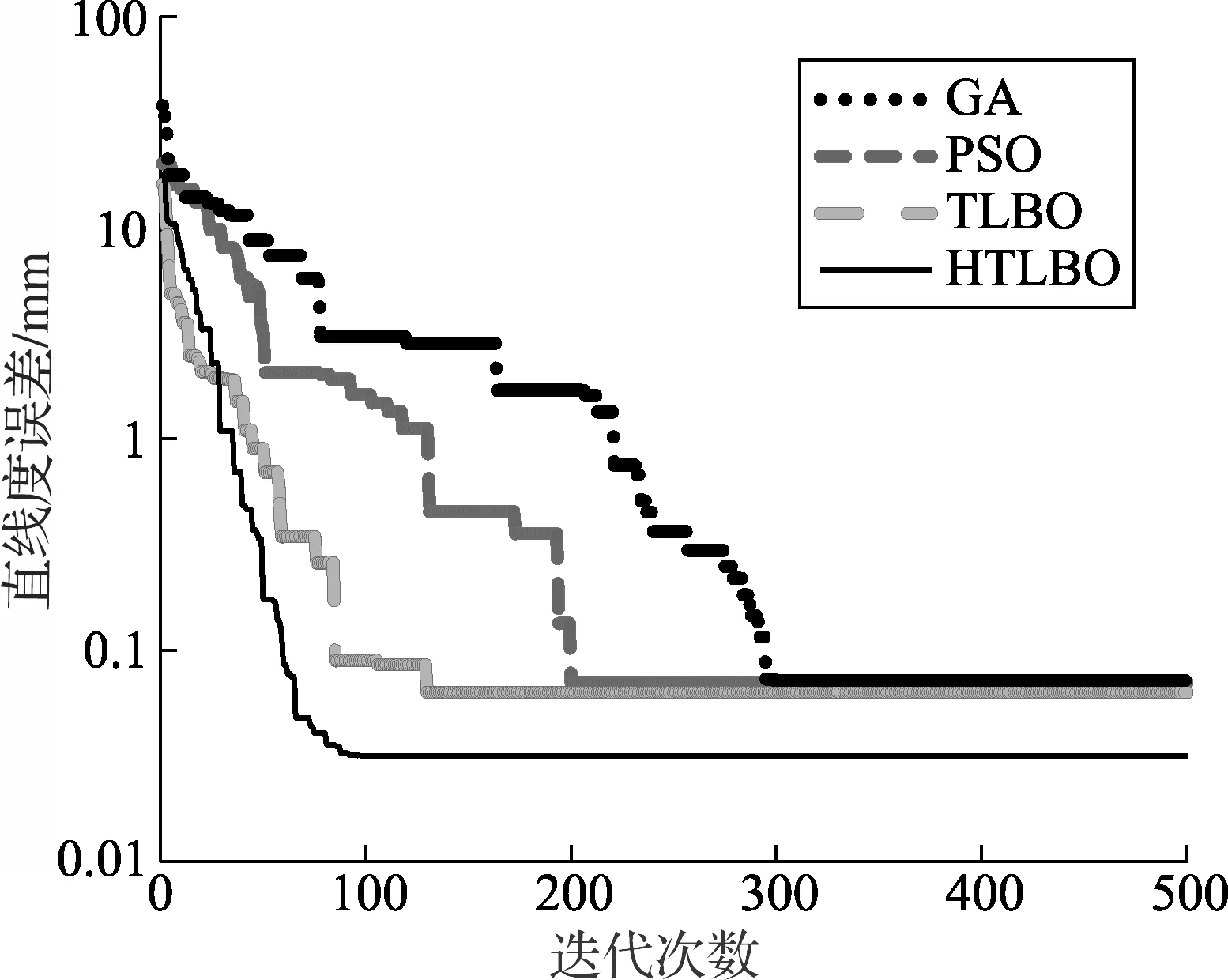
图2 直线度误差曲线
4.2 空间直线度算例2
为了进一步验证HTLBO算法对于评定空间直线度误差的有效性,选取文献[12]中算例的数据和文献[13,15]计算结果对算法进行实验验证。HTLBO程序参数设置与算例1相同,测点数据如表4所示,数据来源于文献[12]。
表4数据的HTLBO算法和文献[13,15]的PSO、LA-AFSA计算结果如表5所示。
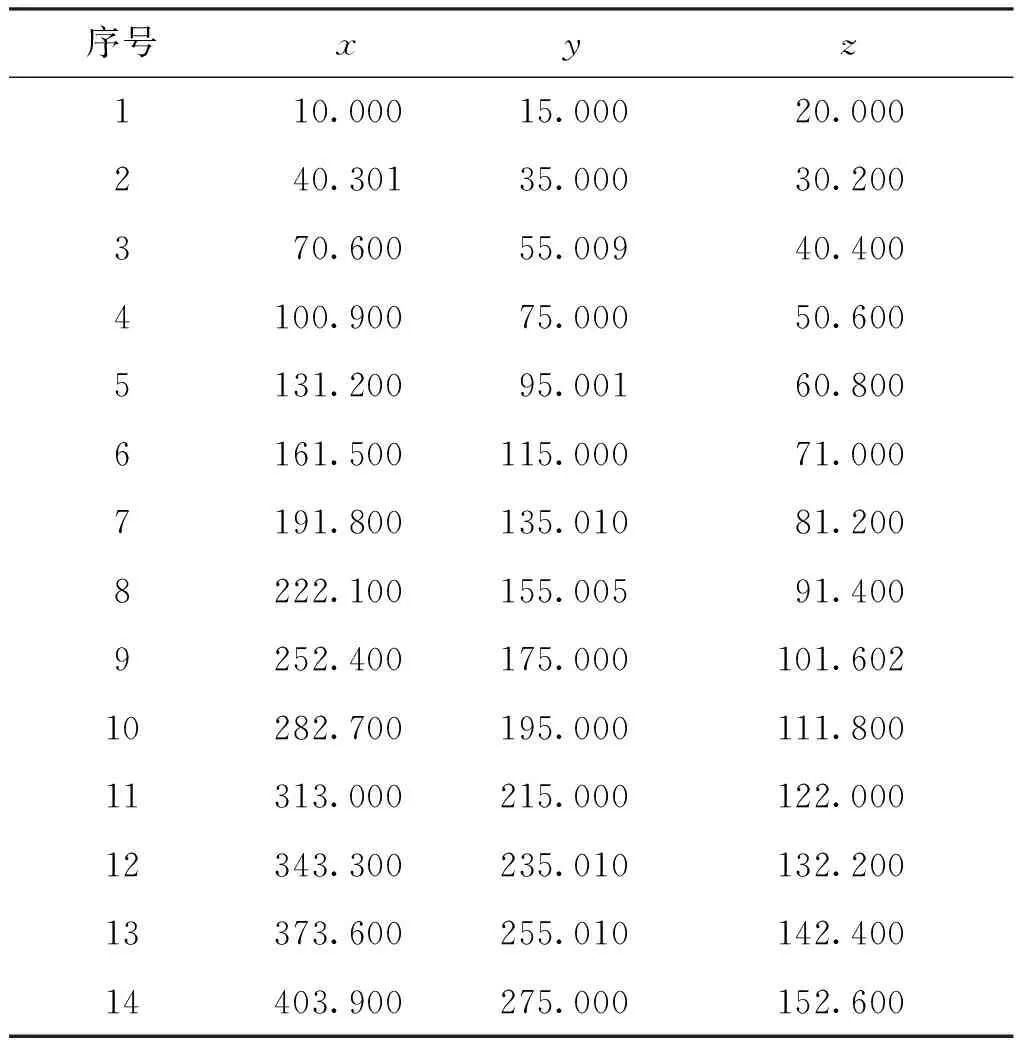
表4 算例2测点数据[12] mm
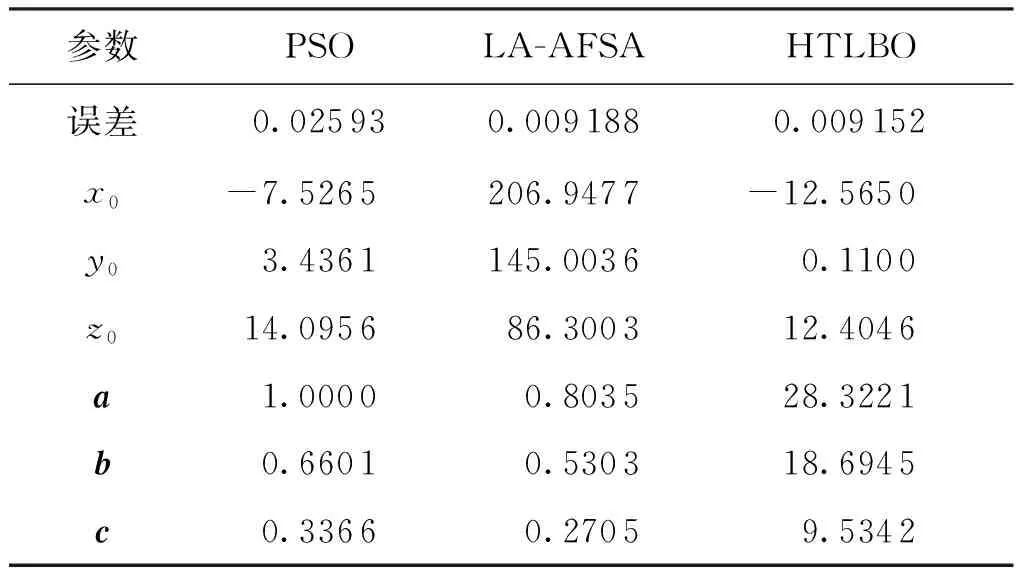
表5 3种算法参数的计算结果 mm
文献[15]中详细列出了其他相关文献的计算结果,结合起来可以看到,相对于传统的非线性求解方法,智能优化算法不仅能够得到测点数据的空间直线度误差值,还可以获得测点最小包容圆柱的方程参数,计算结果更加全面。在智能优化算法的计算结果中,HTLBO算法的计算精度更高,求得的空间直线度误差为0.009 152 mm,最小包容圆柱参数的中心轴线参数方程为F(x0,y0,z0,a,b,c)=F(-12.565 0,0.110 0,12.404 6,28.322 1,18.694 5,9.534 2)。图3为HTLBO算法的迭代曲线,当迭代到102次时,算法达到收敛状态,相对于PSO的344次,收敛速度得到了提高。
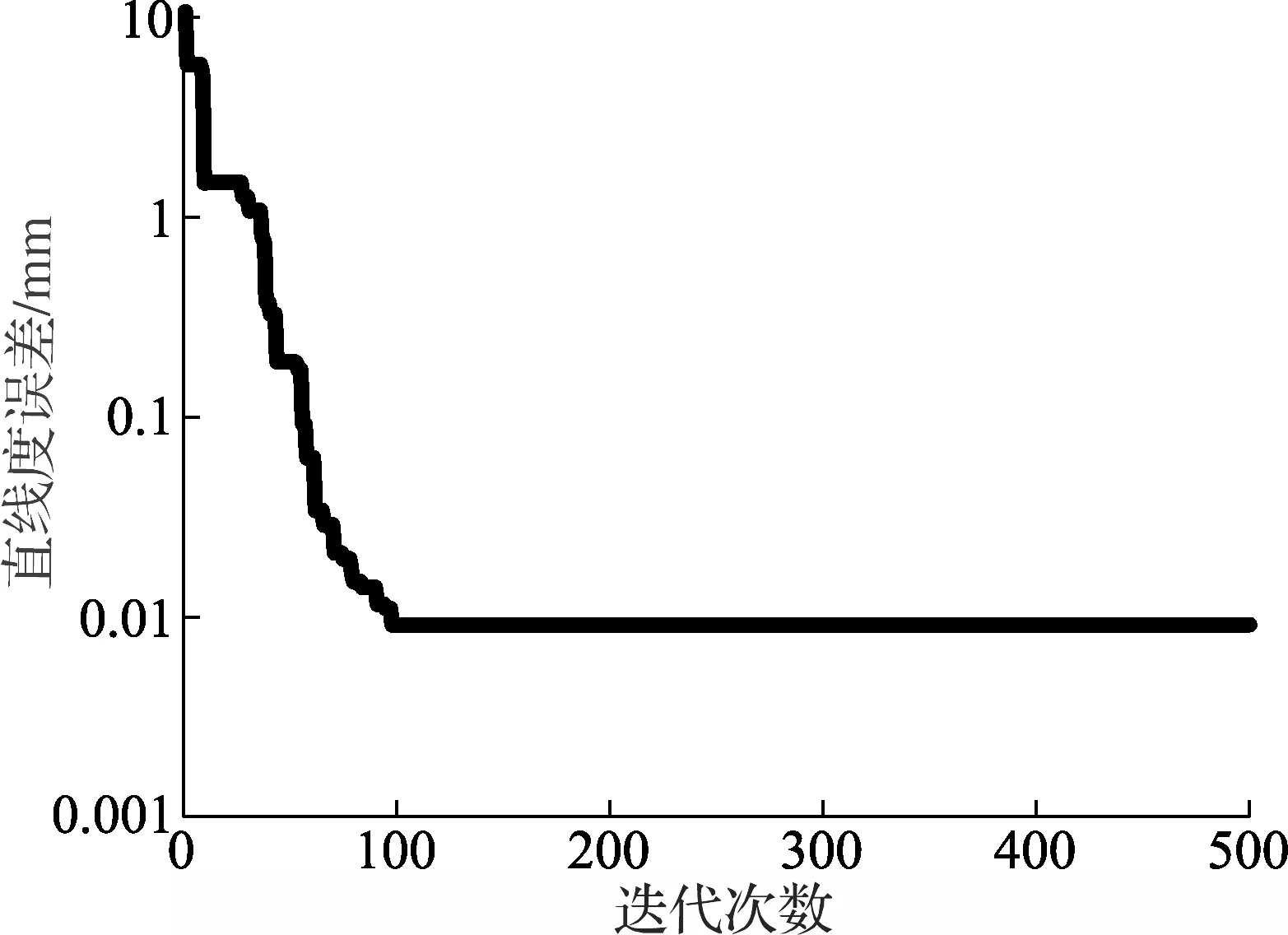
图3 HTLBO迭代曲线
5 结 论
应用TLBO对空间直线度误差进行误差评定,通过引入SFLA的算法优点,设计了一种HTLBO算法,从而进一步增强了算法的全局和局部搜索能力。通过两组算例,得到以下结论:
(1)在满足最小区域准则的条件下,将空间直线度的数学模型和获取的测量数据代入智能优化算法求解,不仅可以得到比最小二乘法等传统非线性求解方法精度更高的空间直线度误差结果,而且同样可以获得包容所有测点的最小圆柱轴线的方程参数,计算结果全面、准确。
(2)从智能优化算法的计算结果可以看出,相对于GA、PSO、TLBO等算法,HTLBO算法搜索能力更强,收敛速度更快,计算精度较高,同样适用于空间直线度的高精度评定领域。
[参考文献]
[1] ANSI/ASME Y14.5 National standard on dimensioning and tolerancing[S]. 2009.
[2] ISO/TS 12780-1:2012 Geometrical product specifications(GPS)-Straightness—Part 1:Vocabulary and parameters of straightness[S], 2012.
[3] Huang S T, Fan K C, Wu J H. A new minimum zone method for evaluating straightness errors[J].PrecisionEngineering, 1993, 15(3):158-165.
[4] Kanada T, Suzuki S. Application of several computing techniques for minimum zone straightness[J].PrecisionEngineering, 1993, 15(4):274-280.
[5] Carr K, Ferreira P. Verification of form tolerances part I: Basic issues, flatness, and straightness[J].PrecisionEngineering, 1995, 17(2):131-143.
[6] Samuel G L, Shunmugam M S. Evaluation of straightness and flatness error using computational geometric techniques[J].Computer-AidedDesign, 1999, 31(13):829-843.
[7] Huang J. An exact minimum zone solution for three-dimensional straightness evaluation problems[J].PrecisionEngineering, 1999, 23(3):204-208.
[8] Ding Y, Zhu L M, Ding H. A unified approach for circularity and spatial straightness evaluation using semi-definite programming[J].InternationalJournalofMachineTools&Manufacture, 2007, 47(10):1646-1650.
[9] Ding Y, Zhu L M, Ding H. Semidefinite programming for Chebyshev fitting of spatial straight line with applications to cutter location planning and tolerance evaluation[J].PrecisionEngineering, 2007, 31(4):364-368.
[10] 雷贤卿, 薛玉君, 李济顺,等. 基于网格搜索算法的空间直线度误差评定方法[J]. 计量学报, 2009, 30(2):115-119.
[11] Cho S, Kim J Y. Straightness and flatness evaluation using data envelopment analysis[J].TheInternationalJournalofAdvancedManufacturingTechnology, 2012, 63(5):731-740.
[12] 廖平, 喻寿益. 基于遗传算法的空间直线度误差的求解[J]. 中南大学学报(自然科学版), 1998, 29(6):586-588.
[13] 茅健, 曹衍龙. 基于粒子群算法的空间直线度误差评定[J]. 工程设计学报, 2006, 13(5):291-294.
[14] 张玉梅, 左春柽, 刘岩,等. 基于人工免疫算法的轴线直线度误差评定[J]. 计量学报, 2010, 31(6):490-493.
[15] 叶明, 唐敦兵. 最小二乘与鱼群混合优化方法评定直线度误差的研究[J]. 机械科学与技术, 2014, 33(7):1013-1017.
[16] Rao R V, Savsani V J, Vakharia D P. Teaching-learning-based optimization: A novel method for constrained mechanical design optimization problems[J].Computer-AidedDesign, 2011, 43(3):303-315.
[17] Rao R V, Savsani V J, Balic.J. Teaching-learning-based optimization algorithm for unconstrained and constrained real-parameter optimization problems[J].EngineeringOptimization, 2012, 44(12):1-16.
[18] Rao R V, Savsani V J, Vakharia D P. Teaching-Learning-Based Optimization: An optimization method for continuous non-linear large scale problems[J].InformationSciences, 2012, 183(1):1-15.
[19] 拓守恒, 雍龙泉, 邓方安. “教与学”优化算法研究综述[J]. 计算机应用研究, 2013, 30(7):1933-1938.
[20] Eusuff M M, Lansey K E. Optimization of water distribution network design using the shuffled frog leaping algorithm[J].JournalofWaterResourcesPlanning&Management, 2003, 129(3):210-225.
[21] Rahimi-Vahed A, Mirzaei A H. Solving a bi-criteria permutation flow-shop problem using shuffled frog-leaping algorithm[J].SoftComputing, 2008, 12(5):435-452.
