一种基于多步法的高精密主轴回转误差分离算法

乔凌霄， 陈江宁， 陈文会， 张 丽， 田景志

(1. 西北工业大学 电子信息学院， 陕西 西安 710072； 2. 西安轻工业钟表研究所有限公司， 陕西 西安 710061； 3.中航动力股份有限公司 计量中心， 陕西 西安 710021)

1 引 言

随着现代科学技术的发展，精密机械、空间技术和军事科学等许多领域对超精密圆形工件提出了越来越高的要求。采用误差分离技术，即从测量数据中分离出圆度误差，可以很好地应用于高精密回转轴系的检测。目前误差分离技术比较成熟，主要分离方法包括多步法、多点法和反向法。多点法需要多个机械特性相似的测头，很难保证测量数据的一致性；反向法只能反映一个方向的敏感误差；而多步法存在谐波抑制的问题[1～3]。在多步法的基础上，本文提出了频域混合补偿法。将多步法中的谐波进行频域补偿，更精确地分离出圆度误差。通过实验对多步法和频域混合补偿法进行了比较，验证了该方法的可行性，运用最小二乘法对分离结果进行评定并做出分析比较。

2 频域混合补偿法基本原理

2.1 测量方案

在高精密主轴系统的回转误差测量中，由于主轴横截面的圆度误差通常远远大于主轴回转误差，如果用传感器测头直接对主轴的横截面外轮廓进行测量，由于截面的圆度误差比主轴回转误差大出一个数量级，将无法进行误差分离。因此，在对高精密主轴系统进行测量时，一般需要借助标准球进行测量,测量系统示意图如图1所示。

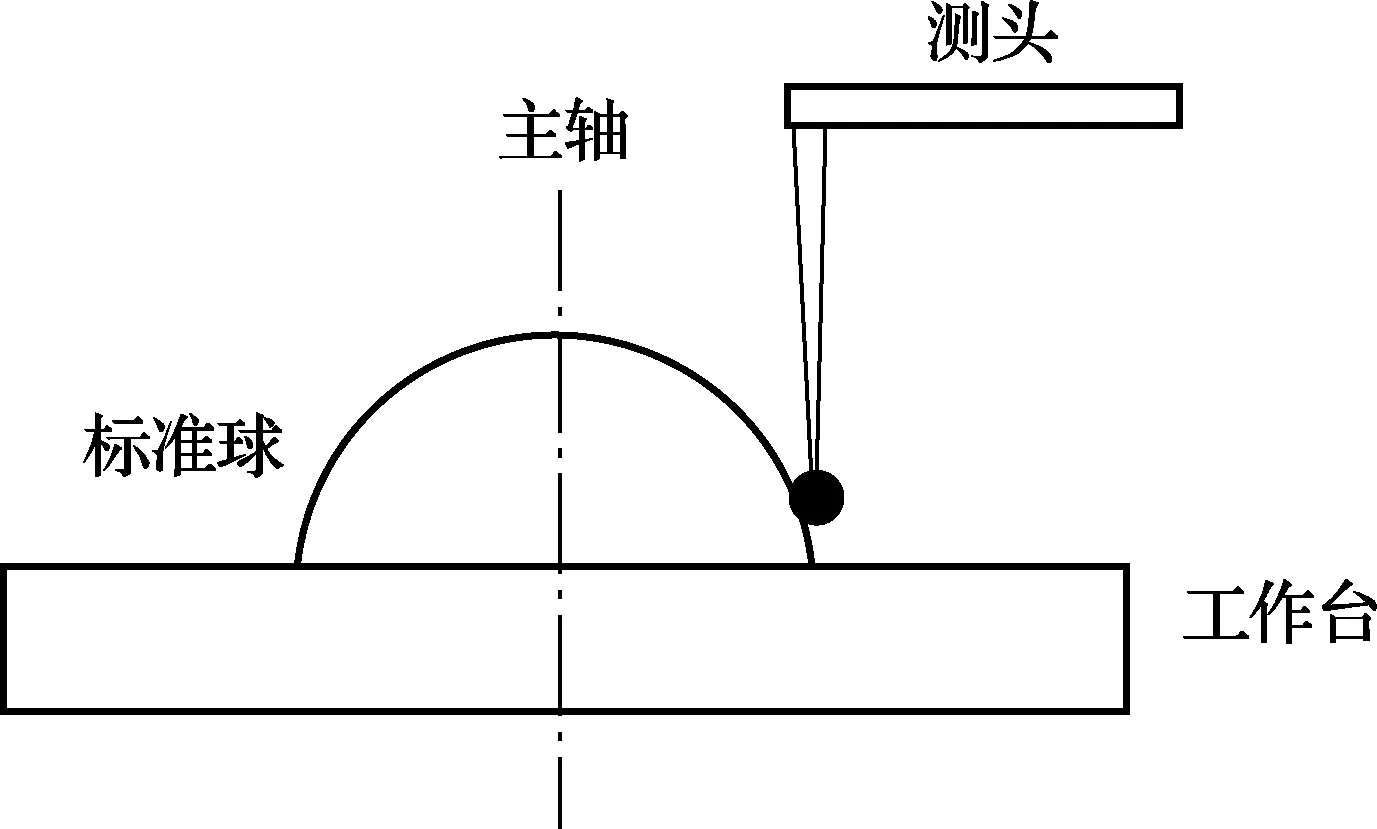
图1 测量系统示意图

本文采用混合多步法的测量方法，即分别以三步、四步、五步为基准的方法。图2为三步法测量采样示意图，测头分别以0°、120°、240°为固定起点测量一圈的数据。每隔1°采集一个点，因此一圈的采样点数为360个，共获取3组数据，每组数据360个值。

图2 三步法测量采样示意图

三步法具体测量步骤如下：

① 测头以0°方向为起始点开始测量，操作仪器使主轴均匀地旋转360°，每1°读取一次读数并记录，仪器测量n圈，并计算出全部数据的平均值作为第1组的数据。

② 测头保持不动，设置仪器参数，使球与轴一起相对于零度转动120°，转动后球的偏心会同时改变，操作仪器再次做调心的步骤，仪器测量n圈，计算出平均值作为第2组的数据。

③ 重复上述测量步骤，测头保持不动，设置仪器参数，使球与轴一起相对于零度转动240°，调心，计算平均值，得到第3组的数据。

同理，四步法分别取0°、90°、180°、270°为起点，五步法分别取0°、72°、144°、216°、288°为起点。重复三步法的步骤，仅需改变转动的角度。

2.2 误差分离过程

在主轴回转误差的测量中，误差分离技术被用于将标准球形状误差(圆度误差)及标准球安装带来的偏心误差从测量数据中分离并剔除。

主轴理想轴心的径向误差无法通过直接测量获得，本文试验中采用了将标准球安置在主轴上，通过测量主轴转动过程中标准球横截面的外轮廓来间接获得。因此,得到的误差除了剔除主轴回转误差外，还混入了标准球的形状误差(圆度误差)、偏心误差，又由于使用了不同起点多次测量的测量方法而混入了角度偏转误差。

实际测量中，由于机器自动调角将角度偏转误差控制在可以忽略的范围内、又可不考虑角度回转误差，因此，最终需要分离的误差成分为：主轴回转误差(径向)、圆度误差、偏心误差。即：

Sn(i)=S(i)-R

(1)

Sn(i)=q+h(i)+rn(i)

(2)

式中：Sn(i)为n组测量误差；S(i)为测量所得的原始数据；R为标准半径(标准球横截面半径与测量臂臂长之和，由仪器给出)；q为偏心误差；h(i)为主轴回转误差；rn(i)为n组圆度误差。

2.2.1 剔除偏心误差

测量误差中的一次谐波分量表示为标准球偏心误差，可以通过傅里叶变化求出测量误差中的一次谐波分量，减去此分量，从而剔除测量误差中的偏心误差[1]。

求出一次傅里叶级数系数：

(4)

将计算结果展开成一次傅里叶级数:

(5)

剔除偏心所造成的一次谐波分量

(6)

2.2.2 分离圆度误差

分离圆度误差的关键在于理解标准球的轮廓是不变的，因此标准球上圆度误差的值是固定的。在测量数据中，由于每次测量的起点不同，故每组圆度误差之间只有相位变换的差别。

即，若设第n组圆度误差为rn(i)、起点相位为in，则有如下的关系：

rn(i)=r1(i-in)

(7)

将第一组圆度误差(相移前的圆度误差)定义为总圆度误差。则有：

r0(i)=r(i)

(8)

对于主轴回转误差而言，每一轮数据测量虽然对标准球做了相移，但是主轴仍然是以原来的零点开始旋转的，因此，每一组数据中的主轴回转误差是固定的。根据主轴回转误差的这个特点，并结合文中提到的圆度误差的特点，可以得到式(9)中的关系[4～11]：

(9)

式中:M表示测量组数。

此时设置权函数g=(g0,g1,…,gM-1)，使等式(9)两边同时乘g可得到：

=g0[r0(i)+h(i)]+g1[r1(i)+h(i)]+

…+gM-1[rM-1(i)+h(i)]

=[g0r0(i)+g1r1(i)+…+gM-1rM-1(i)]+

[g0h(i)+g1h(i)+…+gM-1h(i)]

(10)

由式(10)化简可得到：

(11)

(12)

SX(k) =DFT[g0r0(i)+g1r1(i)+…+gM-1rM-1(i)]

=g0R0(k)+g1R1(k)+…+gM-1RM-1(k)

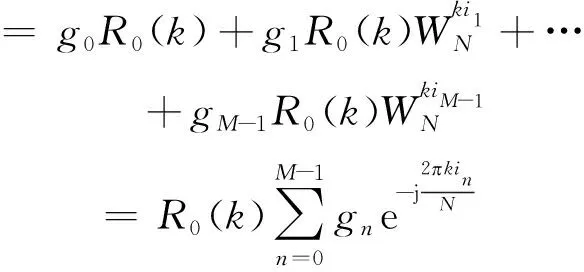
(13)

SX(k)=R0(k)G(k)

(14)

r0(i)=IDFT[R0(k)]

(15)

式中：SX(k)为Sx(i)进行离散傅里叶变换后的结果；G(k)是误差分离的权函数；IDFT为离散傅里叶变换的逆变换。

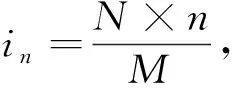
则有：

(16)

根据式(15)与(16)可求得圆度误差r0(i),根据式(6)可求得主轴回转误差为：

(17)

2.2.3 谐波分析与补偿

根据式(17)可以发现，当k=nM时，G(k)=0。这说明，用上述步骤所求得的圆度误差丢失了采样圈数M的整数倍次的谐波分量，再经过式(18)的运算，这些谐波分量就混入了所求的主轴回转误差中，造成了所求值与真实值存在的差异，这就是所谓的谐波抑制。

根据GB 7235—2004规定:圆度误差测量时仪器的频率响应范围为1～50 upr[12]。当谐波次数大于50时谐波抑制的影响可以忽略不计，由于3×4×5=60>50，因此可取M为3、4、5分别计算圆度误差，再通过补偿得到在允许精度内的圆度误差。

经过以上所列出的步骤按顺序分别求出3次转位时的圆度误差的DFT:R3(k)，4次转位时的圆度误差的DFT:R4(k)，5次转位时的圆度误差的DFT:R5(k)。

在3次转位时求得的圆度回转误差中，丢失了3、6、9、12、…次谐波；在4次转位时求得的圆度回转误差中，丢失了4、8、12、20、…次谐波；在5次转位时求得的圆度回转误差中，丢失了5、10、15、20、…次谐波。

当丢失的谐波分量次数n是3的倍数、不是4的倍数时，按照上文所述，将R4(k)中的n次谐波分量补入R3(k)缺少的3的倍数、不是4的倍数次的谐波分量。即令：

R3n(k)=R4n(k)

当丢失的谐波分量次数n是3与4的公倍数，即12的倍数次谐波分量时，可以看到，将R3(k)中的n谐波分量用R5(k)中的n次谐波补偿。即令：

R3n(k)=R5n(k)

因此补偿后的圆度误差仅丢失了n是3×4×5=60的倍数时的n次谐波分量。

3 实验过程与分析

实验数据通过某公司的Talyrond 265圆度仪进行采集，具体采集方法上文已经详细介绍。共采集10组数据，每组数据360个点，总共3 600个数据点。采集数据后，分别用三步法、四步法、五步法以及频域混合多步法对数据进行处理与仿真分析。

3.1 偏心误差分离前后仿真分析

对4种误差分离方法采用同样的方法进行偏心误差的剔除。为了更直观地感受偏心误差分离前与分离后的区别，对偏心误差分离前的数据进行了仿真，见图3。图3中的外圆为原始数据仿真，半径为10 μm的基圆，内圆是传感器采集的数据。

图3 偏心误差分离前后的仿真图

通过对比可以看出，图3(a)偏心误差分离前，数据主要集中在左半平面，数据轮廓的圆心大致位于90°到180°之间，图3(b)的数据分布于原点附近，数据轮廓的圆心与原点基本重合，偏心误差明显已经剔除。

3.2 多步法仿真分析

为了对比不同方法，本文也用多步法进行了误差分离。分别使用三步法、四步法、五步法进行实验仿真。由于这3种方法原理一致，以下仅给出了三步法的误差分离实验仿真分析。

图4、图5分别是圆度误差和主轴回转误差在极坐标系下的仿真图，为了方便观察加了半径为 200 nm 的基圆。

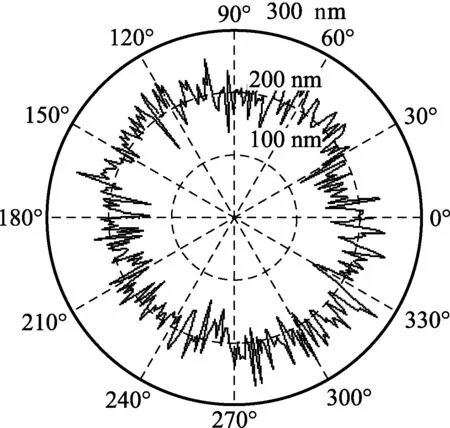
图4 圆度误差

图5 主轴回转误差

图6、图7分别是圆度误差和主轴回转误差在直角坐标系下的仿真图，可以看到圆度误差最大幅值约为78 nm，主轴回转误差的最大幅值约为80 nm。

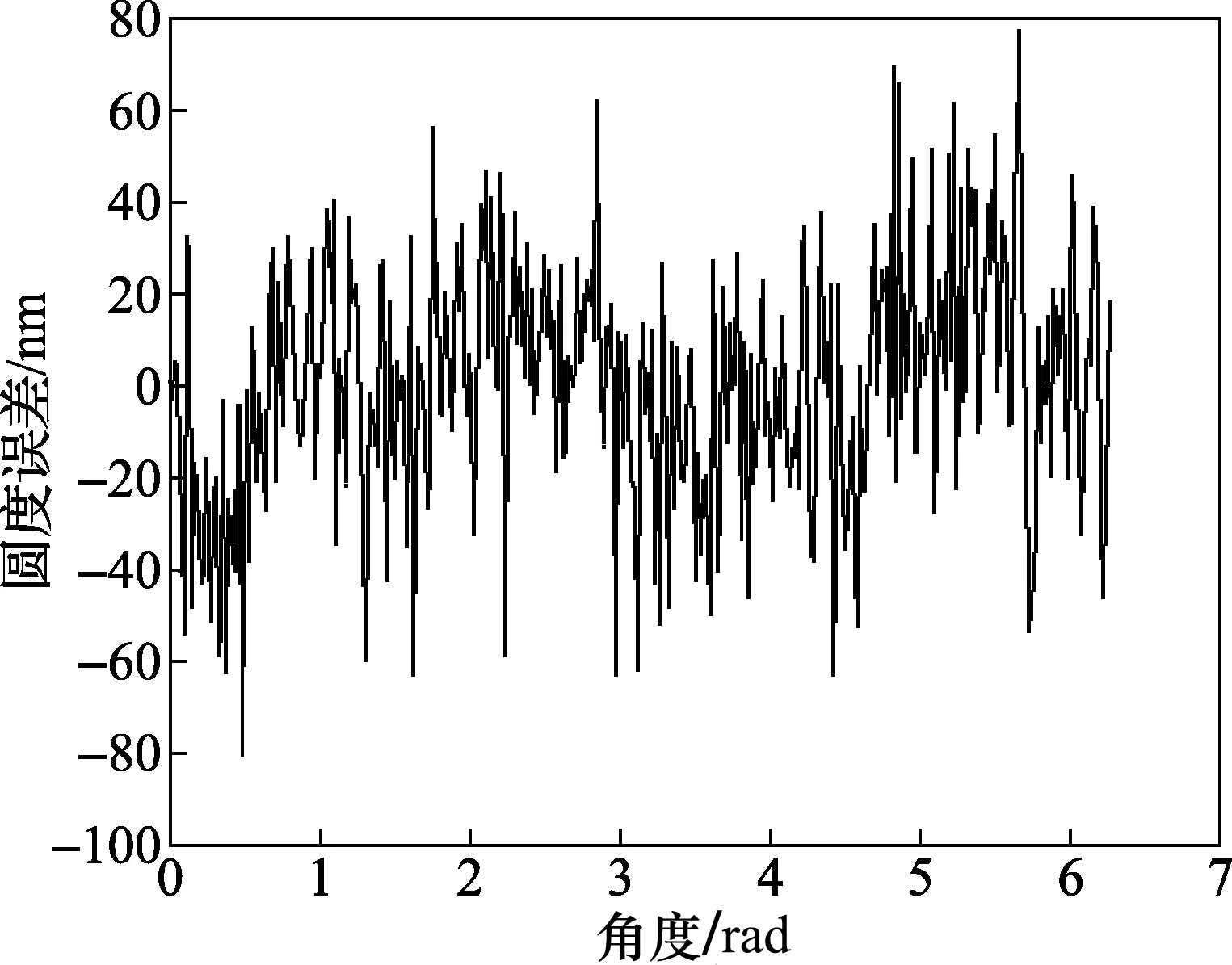
图6 圆度误差

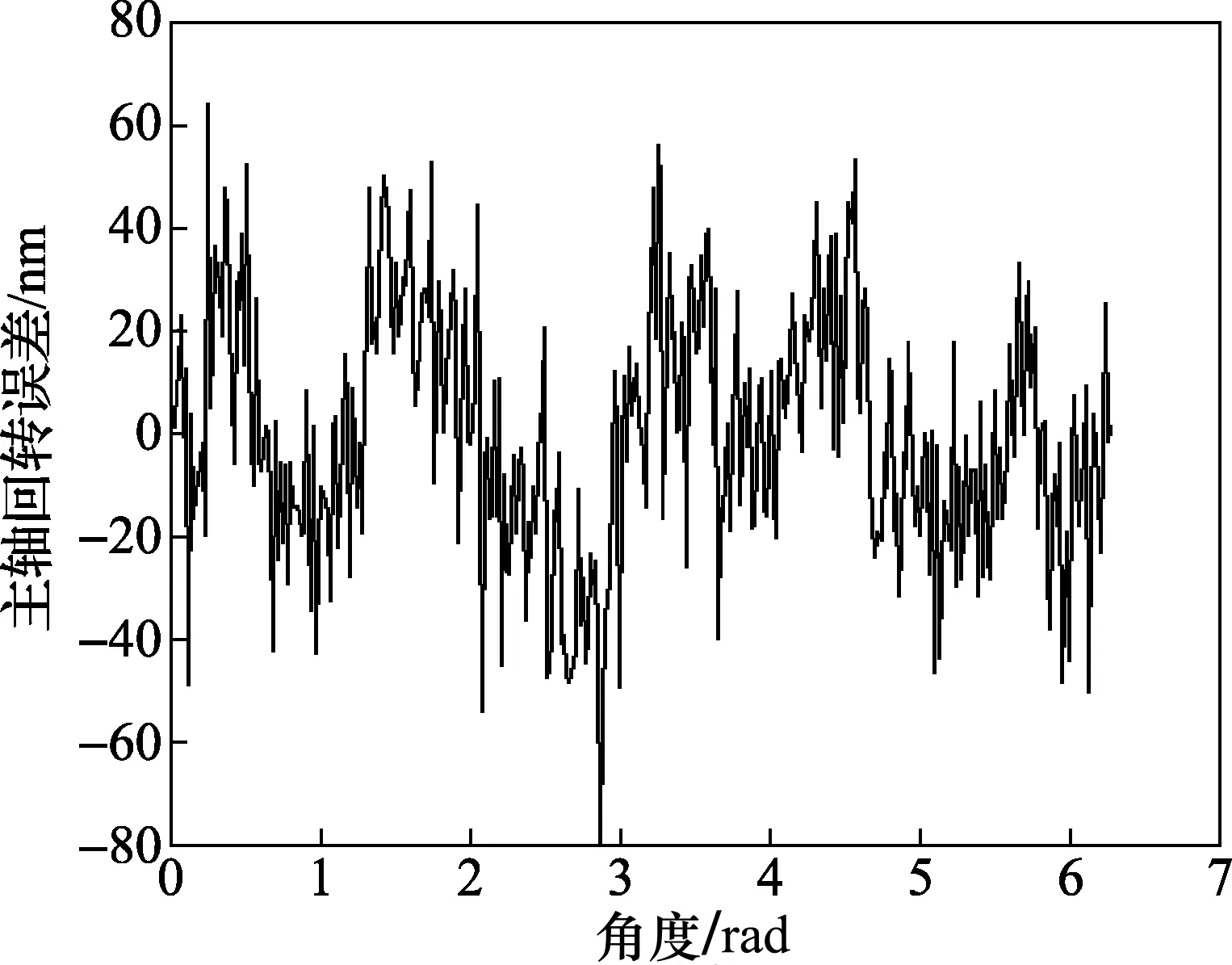
图7 主轴回转误差

3.3 频域混合补偿法仿真分析

经过误差分离后得到了独立的主轴回转误差和圆度误差，两组数据都是360个离散的点，图8、图9分别是圆度误差和主轴回转误差在极坐标系下的仿真图，为了方便观察加了半径为200 nm的基圆。

图8 圆度误差

图9 主轴回转误差

图10、图11分别是圆度误差和主轴回转误差在直角坐标系下的仿真图，可以看到圆度误差最大幅值约为37 nm，主轴回转误差的最大幅值约为80 nm。

3.4 圆度误差与主轴回转误差的评定

图10 圆度误差

图11 主轴回转误差

为了验证频域混合补偿法的优良性，分别用三步法、四步法、五步法进行了误差分离，对得到的圆度误差及主轴回转误差采用了最小二乘圆法[13～17]进行了误差评定，评定结果见表1。

表1 不同方法的误差评定结果 nm

圆度误差评定值与标准球的圆度误差值40 nm间的差值分别为118 nm、113 nm、145 nm; 而频域混合补偿法分离出的圆度误差评定值为54 nm，与给出的圆度误差40 nm仅相差14 nm，可以看出频域混合补偿法对误差的分离效果明显优于多步法的误差分离效果。

4 结 论

频域混合多步法误差分离技术的应用极大地提高了精密测量精度,很好地消除了多步法圆度误差分离时出现的谐波抑制,基本可以实现圆度误差和主轴回转误差的完全分离。

[参考文献]

[1] Peng H,Wu Y,Wang B,etal. An improved two-point real-time measuring method for radial micro-displacement measurement on high-speed smart boring bar[J].TheInternationalJournalofAdvancedManufacturingTechnology,2015,81(5):925-933.

[2] 苏文宇.主轴回转精度测试实验系统改造及其误差分析[D].哈尔滨：哈尔滨工业大学，2010.

[3] Ma P,Zhao C,Lu X,etal. Rotation error measurement technology and experimentation research of high-precision hydrostatic spindle[J].TheInternationalJournalofAdvancedManufacturingTechnology,2014,73(9):1313-1320.

[4] Liu C H,Jywe W Y,Lee H W. Development of a simple test device for spindle error measurement using a position sensitive detector[J].MeasurementScience&Technology,2004,15(9):1733-1741.

[5] 刘敏. 超精密主轴回转精度测试研究[D].哈尔滨：哈尔滨工业大学,2007.

[6] 高西全,丁玉美.数字信号处理[M]. 3版. 西安：西安电子科技大学出版社，2008:75-87.

[7] 任东旭.回转误差分离技术研究[D].郑州：中原工学院，2009.

[8] Xiang K,Wang W,Zhang M,etal. Nonlinear analysis of cylindrical capacitive sensor used for measuring high precision spindle rotation errors[J].ProceedingsofSPIE-TheInternationalSocietyforOpticalEngineering,2015,9446(2):167-78.

[9] 陈永当,李少康.圆度测量误差分离方法[J].西安工业学院学报，2000，20(4):327-332.

[10] 雷贤卿,李言,李济顺,等. 多步法圆度误差分离的演化形式及其谐波抑制分析[J].工业仪表与自动化装置，2006，(1):45-46.

[11] 赵维谦,谭久彬,杨文国,等. 基于两步法超精密圆度仪误差分离系统[J]. 中国机械工程,2000,11(11):1206-1208.

[12] GB/T 7235-2004 产品几何量技术规范(GPS)评定圆度误差的方法半径变化量测量[S]. 2004.

[13] 冯兰芳.圆度误差评判的最小二乘圆法[J].郑州工业高专学报，1996,12(1):5-8.

[14] Li Y,Liang L,Gao F. Thermal error measurement and rotation accuracy evaluation of CNC lathe spindle[J].ChinaMechanicalEngineering,2015,26(12):1611-1615.

[15] 雷贤卿，高作斌，马文锁,等. 基于几何搜索逼近的球度误差最小区域评定[J].计量学报, 2016,37(2):123-127.

[16] 刘庆民，张蕾，吴立群,等. 基于机器视觉的非均匀分布点圆度误差评定[J].计量学报, 2016,37(6):567-570.

[17] 丁玲.圆度与圆柱度误差评定算法的设计与应用[D]. 西安：西安电子科技大学，2013.