一种光电自准直仪空间坐标系建立方法研究
2018-06-22杨占立范百兴王成江王瑞鹏
杨占立, 范百兴, 西 勤, 王成江, 王瑞鹏
(1.解放军信息工程大学, 河南 郑州 450001; 2.海克斯康测量技术(青岛)有限公司, 山东 青岛 266100; 3.青岛市勘察测绘研究院, 山东 青岛 266033)
1 引 言
目前,大多数光电自准直仪采用的二维敏感器件主要应用于航空航天立方镜的准直测量,机械制造中同轴度、直线度、平面度的测量[1,2],计量测试中测角设备的精度检测等。由于光电自准直仪具有测量精度高、灵敏度高、自动化程度高、分辨率高、使用简单等特点,被广泛应用于测量的各个领域[3-8]。
对光电自准直仪的应用目前只局限在单台对单个目标的测量上,对实现多台、多目标的联合测量的研究则鲜见报道。联合测量是一种根据测量对象、精度要求、测量环境等条件融合多种传感器的测量方法,旨在解决工业测量领域自动化程度不高、测量精度低等多种难题。本文提出一种光电自准直仪自身坐标系建立的方法,根据其内部结构和测量原理,建立空间虚拟直角坐标系,并建立二维角度观测值(x,y)与直角坐标系下的水平角α和垂直角β的转换模型,对实现光电自准直仪与多传感器的联合测量打下基础。
2 光电自准直仪工作原理
2.1 光电自准直原理
图1为光电自准直仪的光学成像原理图。光源发出的发散光通过圆孔目标,透过分光镜到达准直物镜转换为平行光直接照射到反射镜上,然后沿原光路返回,再次到达分光镜并反射至敏感器件。当反射镜产生α偏角时,反射回敏感器上的光电位置也将发生变化[5,7]。
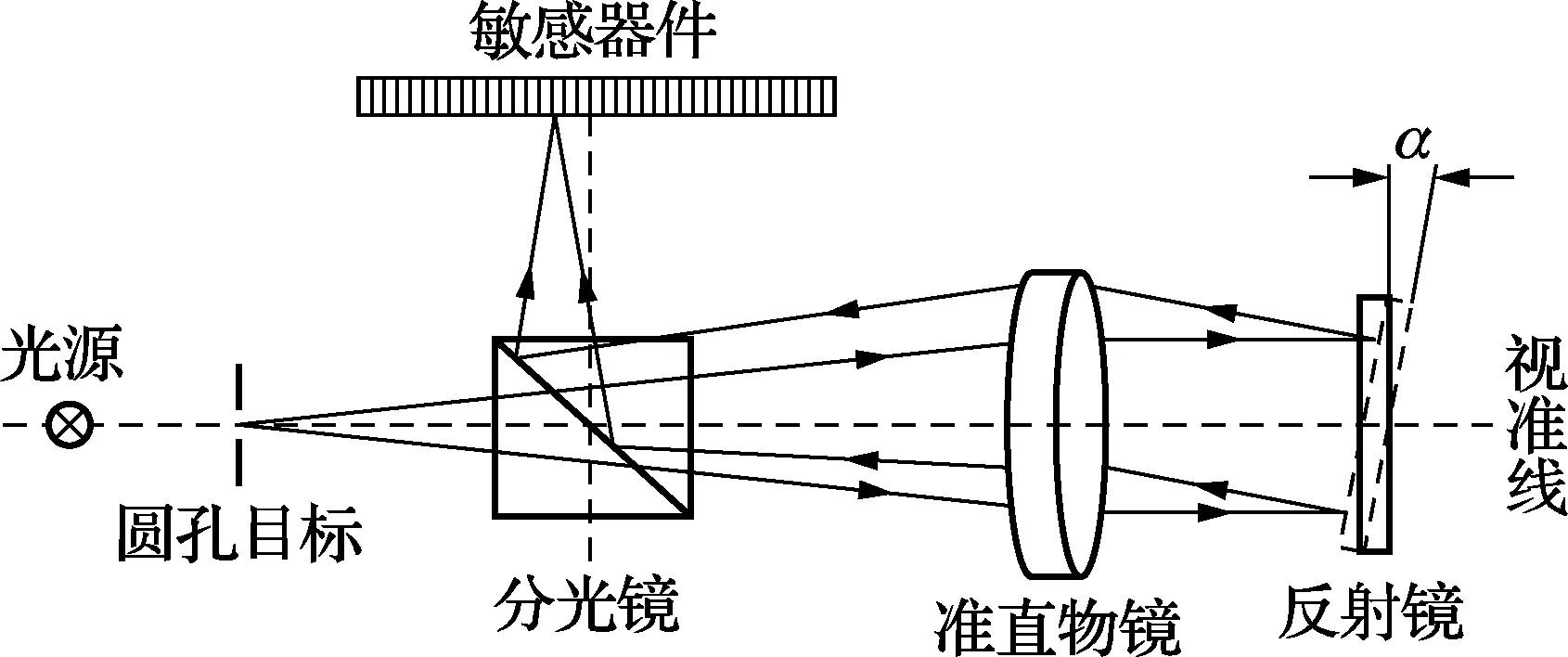
图1 光电自准直原理图
根据光学原理,反射镜的偏角α与准直物镜焦距f′及反射光在敏感器件上的位移量S有如下的关系:
S=2f′ tanα
(1)
光电自准直仪是一种小角度测量仪器,因此α比较小,式(1)可近似写为S=2f′α。在光电自准直仪中f′是一个常数,需通过测量接收器上的位移量即可得到反射镜的偏角α。
2.2 敏感器件工作原理
在光电自准直仪中,敏感器件的作用是将接收到的光信号转换为电信号,随着光电位置的变化导致电信号的变化,记录电信号的变化来确定光点位移量,即可通过公式(1)解算得到反射镜的偏角。
根据敏感器件的不同,光电自准直仪角度测量数据分为一维和二维,目前大多数的光电自准直仪采用二维的敏感器件,主要有位置敏感器件(position sensitive detector,PSD)和电耦合元件(charged coupled device,CCD)两种。
PSD器件是一种基于横向光电效应的光能/位置转换器件,以模拟量的形式将位置量进行输出,是一种非线性转换方式[9],原理图如图2所示。图中X1,X2,Y1,Y2分别为每个电极的光电流输出;(X,Y)为光斑的中心位置坐标;LX,LY分别为光敏面的宽和长。
CCD敏感器件是由一对金属氧化物半导体充电电容与储存电电容耦合而成的相敏单元,光或电刺激使得电路将各个相敏单元收到的光电能信号以电脉冲信号的方式输出[10],进而实现位移量的测量,面型CCD原理图如图3所示。

图3 面型CCD原理图
3 光电自准直仪坐标系
3.1 坐标系的建立
光电自准直仪不同于常规的测量仪器,其本身没有空间坐标系,为了将其与多种测量设备联合使用,本文提出一种虚拟空间坐标系建立方法,并将其应用于光电自准直仪,实现光电自准直仪自身坐标系的建立。
光电自准直仪是在平面坐标系显示二维角度值。以光电自准直仪的视准轴为坐标系的Z轴,该Z轴平行于测量角度值为(0,0)的平面镜法线;X轴定义为光电自准直仪读数为(xi,0)的点所在的直线,以xi值增大方向为正向;同理,Y轴定义为光电自准直仪读数为(0,yi)的点所在的直线,以yi值增大的方向为正向。这里i=0,1,2,…,n;xi,yi表示光电自准直仪角度测量数据。
坐标系原点的确定:当光电自准直仪对反射镜进行准直,其平面坐标值为(0″,0″)时,反射光中心与目镜的交点作为坐标系的原点,也是视准线与目镜的交点。
3.2 参数转换模型
以空间中任意一个平面镜为例,用光电自准直仪对其进行准直测量,并根据光电自准直仪工作原理得到反射光线和平面镜法线在空间坐标系下的位置关系,如图4所示。
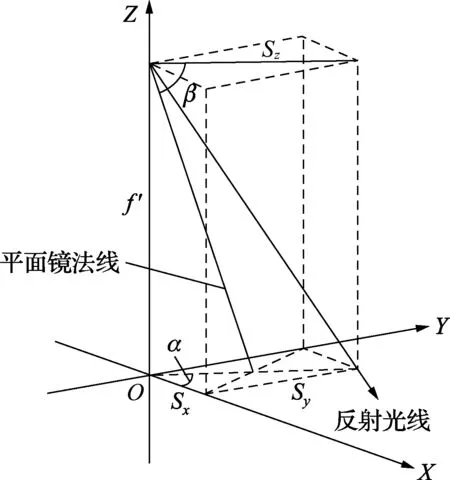
图4 空间直角坐标系
以Sx表示敏感器件得到的x方向的位移量,同理Sy表示y方向的位移量,加上光电自准直仪的观测值(x,y),则可根据(1)可以得到:
(2)
从图4可以得出tanα=Sy/Sx,联立式(2)得到平面镜法线在空间坐标系下的水平角α的计算公式:
(3)

(4)
联立公式(2)得到:
(5)
3.3 模型验证
以光电子准直仪两组观测值(0″,500″)、(0″,-500″)为例,从两组观测值可以看出两平面镜法线的夹角θ=1 000″;根据式(3)和式(5)计算出的平面镜法线在空间坐标系下的水平角和垂直角分别约为(90°, 89.861 1°)、(-90°, 89.861 1°),以这两组数据计算得到的两平面镜法线的夹角θ′=1 000.08″,θ≈θ′,即验证了光电自准直仪空间坐标系建立方法的合理性及参数转换模型的正确性。
因此,式(3)和式(5)即为利用光电自准直仪观测值(x,y)计算平面镜法线在空间坐标系下的水平角α和垂直角β的转换模型。
4 结 论
对光电自准直仪的工作原理及内部结构进行分析,通过虚拟方法建立其空间直角坐标系,推导出参数的转换模型并进行实例验证,为实现光电自准直仪与其他传感器的联合测量提供了理论基础。
[参考文献]
[1] 董彦维,贾军强,万琦,等.一种高精度线阵CCD二维自准直仪四狭缝目标中心的定位方法[J].导弹与航天运载技术,2016,(1):81-84.
[2] 叶声华,樊玉珍.提高激光准直精度的一种有效方法[J].计量学报,1986, 7(4):75-78.
[3] 刘学吉,王省书,周金鹏,等. 光电自准直系统的建模方法研究[J]. 光电技术应用, 2016,37(4): 545-551.
[4] 张小强,武欣,王伟荣,等. 平面光学元件平面度动态干涉拼接测量[J].计量学报, 2016, 37(5): 484-488.
[5] 周丹,向阳,高健. 自准直仪光学系统设计[J]. 应用光学, 2014, 35(5): 794-798.
[6] 刘雯,沈妮,李天初. 用多齿分度台标定激光小角度干涉仪[J].计量学报, 2004,25(4): 298-301.
[7] 周红锋,宫爱玲. 小角度测量的光学方法[J]. 计量技术, 1981,(3): 3-8.
[8] 张之江,于瀛洁. 三维小角度测量系统建模[J].计量学报, 2003, 24(1): 21-25.
[9] 王强龙,潘宏侠,任海峰,等. 基于PSD的长管弯曲度测量系统设计[J]. 传感器与微系统, 2013,32(1): 108-110.
[10] 石东新,傅新宇,张远. CMOS与CCD性能及高清应用比较[J]. 通信技术, 2010,43(12): 174-179.
