TA9管材十辊矫直过程仿真
2018-06-22胡志鑫
王 昌 胡志鑫
(内蒙古科技大学 机械工程学院,包头 014010)
钛及钛合金不仅具有熔点高、无磁性、热膨胀系数低、比强度(材料的强度与其密度之比)和比刚度(材料的弹性模量与其密度的比值)高的综合力学性能,还拥有耐腐性能好、耐生物侵蚀等许多优异特性。TA9合金主要应用于稀盐酸、稀硫酸、稀磷酸环境,也广泛用于钛设备以防止缝隙腐蚀,如用作列管式换热器和纺织的喷丝头等部件。
1 矫直方法及矫直原理
1.1 斜辊矫直法
所谓斜辊矫直法,即上下两个辊子以一定角度交错分布,轧材从上下两排相互交错排列的辊子之间通过时因受到多次反复弯曲而得到的对形状缺陷的矫正,斜辊矫直机多用于管棒材的矫直。
1.2 矫直原理
矫直辊表面呈一定曲线形状,并且与轧件成α角布置。在矫直辊的带动下,轧件既转动又轴向移动,作螺旋前进运动。轧件通过由交错布置的矫直辊所构成的几个弹塑性弯曲矫直单元,各个断面得到多次反弯,达到一定程度的矫直。同时,轧件在旋转中得到不同方向的反弯,也就能够矫直多方向的原始曲率。轧件通过矫直辊时,每转半周弯曲一次,轧件容易得到多次弹塑性弯曲,所以一般斜辊矫直机的辊数不多,构成l~3个弹塑性弯曲单元,就能达到所要求的矫直精度。对于管材,除沿长度方向上弯曲的曲率得到消除或减小外,断面形状也同时得到矫直[1]。
2 矫直参数的计算
2.1 辊子的辊形设计
矫直机的辊子部分结构比较复杂,为了适应有限元的模拟计算,根据矫直机辊子本身的特点,对其进行合理简化,利用SOLIDWORKS建立矫直过程的三维模型,得出的矫直辊轴向的剖线方程如下:
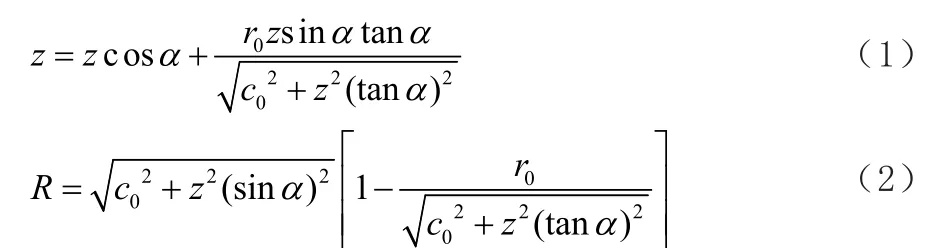
式中,r0为管材半径,mm;R0为矫直辊辊腰半径,mm;c0为辊腰半径与管材半径之和,mm。
利用origin得出辊型曲线及辊子模型,如图1所示。
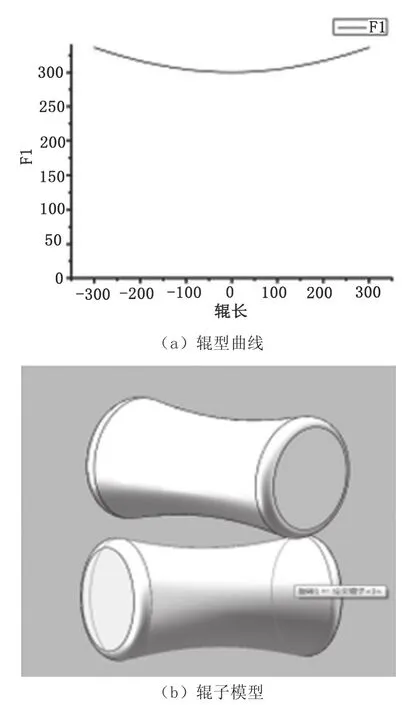
图1 矫直辊辊形曲线及矫直辊模型
2.2 辊子倾角的选择
辊子倾角的取值范围为25°~43°。如果倾角过小,则会降低矫直速度,从而使生产效率下降;倾角过大,辊子与管材的接触线长度过短,接触应力就会变大,越容易产生缺陷。随着倾角的变大,管材旋转一周前进的导程也变大,弯曲矫直次数为弹塑性变形区长度就会减少,这会影响管材的最终矫直质量[2-4]。综合以上因素,笔者选取的辊子角度为α=30°。
2.3 辊长及辊距的选择
其辊距为:

式中,L为辊子全长,L=Lg+2Rg;Rg是辊子两端圆角半径。本文选用的管材直径为7mm,故可得辊距为P=80mm。
2.4 矫直速度的选择
矫直速度是一个影响产量的最直接的因素。但是,工件的转速又要受到其原始的弯曲程度的限制。原始的弯曲过大,工件咬入后的甩摆严重,很容易损坏设备,甚至造成人员伤害。
本文中,速度v=0.36m/s,vg=0.5Dgωg,因Dg=7mm,故ωg=34.28rad/s。
3 有限元模型建立及矫直过程仿真
3.1 模型的建立
本文使用的薄壁细管模型长200mm,为了咬入的方便以及加快计算机的计算速度,将细管分为两部分,即直管部分和弯管部分,设定为直管部分100mm,弯曲部分100mm,弯曲部分是通过螺旋线投影到基准面上而建立的扫描路径,弯管部分设计参照正余弦曲线,管材的原始轴线最大偏差为1.8mm。而管材在矫直过程中的变形都很复染,结合计算机的分析能力和网格的划分情况,在建立十棍矫直过程的有限元模型时,必须进行简化为由五对上下对称布置、呈一定倾斜角度的矫直辊,其模型如图2所示。
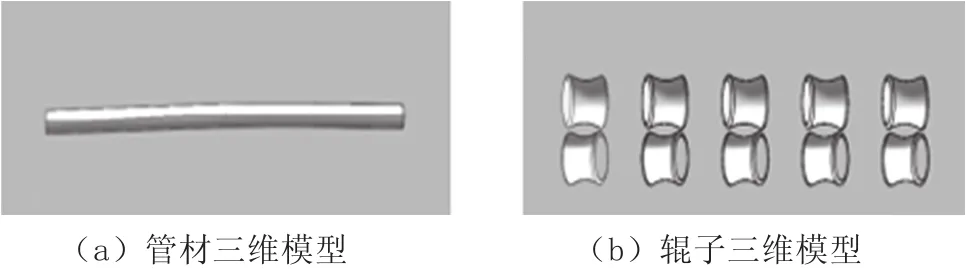
图2 十辊矫直机管材三维模型及辊子三维模型
3.2 矫直过程仿真
管材的整个矫直过程如图3所示,管材在矫直开始阶段,管材经过外部作用进入矫直辊中,矫直辊将管材咬住,此时通过等效应力云图可以看出,管材在咬入过程中,由于管材与矫直辊刚开始接触产生了碰撞,管材受力不均匀,进入矫直辊的端部局部发生了塑性变形,出现了应力集中的现象,并且产生集中应力的部位相对对称,说明了管材很好地进入矫直辊辊腔中。
管材经过咬入阶段,顺利进入矫直辊辊腔,由矫直辊与管材之间的摩擦力带动管材前进。此时,管材由咬入阶段进入稳定矫直阶段。管材的前部分矫直过程可以看出,管材与矫直辊进行了良好的接触,矫直辊系的第一对辊与第三对辊起到了很好的导向作用,使管材的矫直过程平稳进行,管材并未出现摆动、抛出等现象。在矫直过程中,辊子与管材之间接触产生的最大压力在420MPa以下,但大于400MPa,说明辊子与管材之间进行接触时,管材发生弹塑性变形,这符合管材矫直原理。
4 结论
根据斜辊矫直机矫直原理,本文所设计的矫直辊及各种参数符合矫直需求且可以很好地对管材进行矫直。管材矫直过程是反复压弯、压扁,低速咬入、低速抛出,可使管材直线度保持在1.5mm以下。
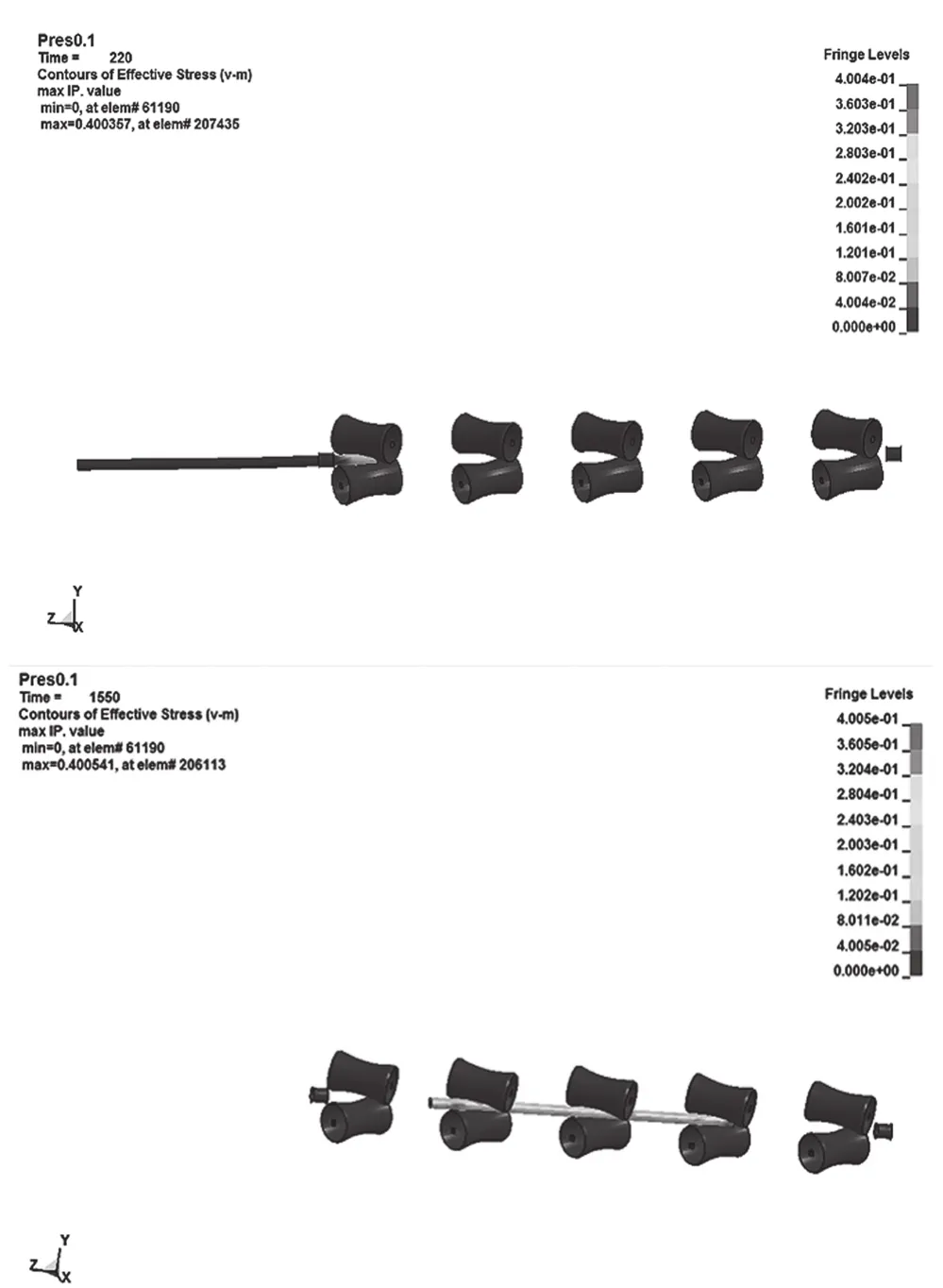
图3 管材矫直过程
[1]崔甫.矫直原理与矫直机械[M].北京:冶金工业出版社,2002.
[2]薛艳杰.6+2复合管材矫直机辊型曲线设计及有限元仿真[D].秦皇岛:燕山大学,2012:7.[3]A M 马斯基列逊.管材矫直[M].北京:机械工业出版社,1978.
[4]连家创.矫直理论与卷曲理论[M].北京:机械工业出版社,
2011.
