基于支路潮流线性化方程的有序充电快速求解方法

张 剑, 姚潇毅, 尹柏强, 何怡刚

(合肥工业大学电气与自动化工程学院, 安徽省合肥市 230000)

0 引言

未来几十年,人类将面临供电安全性、环境紧迫性与能源成本可支付性的巨大挑战[1]。世界经济、社会正在向能源高效和环境友好方向转变。电动汽车在缓解石油危机、减少有害气体排放、平抑可再生能源波动等方面大大优于传统汽车。目前,世界各国都加快了发展电动汽车的步伐。电动汽车对电网的影响及利用等相关问题已成为电气工程领域的研究热点[2-3]。电动汽车有序充电研究主要分为分布式与集中式两种。分布式有序充电主要包括模糊数学理论[4]、交替方向乘子法[5]、灵敏度分析[6]等。集中式有序充电主要包括灵敏度分析[7-8]、模拟进化算法[9-10]、最优化技术[11-19]等。文献[7-8]提出了一种基于灵敏度分析的电动汽车实时控制策略。但只对充电地点进行优化,未对充电功率进行优化,而且电动汽车能否充满电也未知。文献[9-10]将遗传算法应用于电动汽车有序充电。然而,由于遗传算法计算效率较低,难以满足大规模电动汽车接入时在线运行的要求。

由于电动汽车有序充电属于大规模优化问题。国内外专家学者提出了多种方法提高计算速度。文献[11]以网损最小为目标,采用序列凸二次规划与修正节点电压交替迭代直至收敛的算法。文献[12]比较了序列凸二次规划与动态规划算法,指出两者计算结果相近,但是前者的计算时间小于后者。但该方法未计及配电网的三相不平衡与节点电压、支路电流约束。

文献[13-14]以获取最大充电能量为目标函数,将节点电压、配电变压器(简称配变)、线路载流量不等式约束线性化,提出了一种电动汽车有序充电的线性规划模型。但是该方法线性化的误差较大,当应用于计及分时电价的、以车主总充电费用最小为目标函数的优化问题时可能导致节点电压超出下限。文献[15]以电网公司收益最大为目标,将基于直角坐标系的电流型潮流方程等式约束、节点电压、线路载流量不等式约束线性化,提出了一种混合整数线性规划模型。但所采用的线性化技术过于复杂,引入了过多的辅助变量与约束条件,大大增加了模型的复杂度,而且只对充电地点进行了优化,未对充电功率进行优化,构建的混合整数线性规划模型比线性规划模型求解困难得多。

文献[16]计及分时电价与电池老化,提出了一种电动汽车有序充放电的二次规划模型。文献[17]提出了一种计及配电系统容量阻塞的有序充电策略。文献[18]将三相光伏逆变器、充电桩改造成三个独立的单元,用于将负荷从重载相转移至轻载相,提出了一种目标函数兼顾降损与均衡负荷的二次规划模型。文献[19]证明在一定条件下,负荷率、负荷方差与网损存在等价关系,以网损最小为目标可以转化为以负荷方差或负荷率最小为目标,从而简化计算。以上4种方法没有计及节点电压约束。当大量电动汽车接入时,节点电压约束是限制充电功率的重要因素。忽略节点电压约束能够大幅提高计算速度,却可能导致求得的最优充电功率是不可行解。

针对以上文献计算效率低或未计及三相不平衡、节点电压与支路潮流约束的不足,本文推导了三相平衡与不平衡配电网的支路潮流方程,构建了以车主总充电费用最小为目标函数,节点电压、支路功率、充电功率为不等式约束,支路潮流方程、充电需求为等式约束的有序充电模型,提出了将模型非线性项线性化的方法与策略并通过3个仿真算例验证了所提出方法的性能。

1 配电网的支路潮流方程

1.1 三相平衡配电网的支路潮流方程

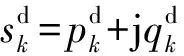
令Hk:={j|(k,j)∈ε}为节点k的子节点集合,支路(i,k)始端的复功率满足:

(1)

节点i的子节点k的电压为:

(2)

式中:*表示共轭；Pik和Qik分别为支路(i,k)的有功和无功功率。

假设配电网的根节点为平衡节点,即

VN+1=Vs=|Vs|∠0°

(3)

其中|Vs|是固定的。将式(2)的左右两边同时乘以其共轭,得到:

(4)

将式(1)的实部与虚部分开,得到:

(5)

(6)

电力负荷一般包含恒功率与恒阻抗负荷,因此负荷功率可表示为:

(7)

(8)

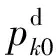
令Ui=|Vi|2,根据式(3)至式(8),三相平衡配电网的方程可简化为:

UN+1=|Vs|2=Us

(9)

(10)

(11)

(12)

(13)

(14)

1.2 三相不平衡配电网的支路潮流方程

实际配电网中,由于架空线路三相一般不再换位,故线路互感矩阵非对角元不相等,而且各相负荷也不相等。因此配电网三相不对称。对于每条支路(i,k)∈ε,电压方程为:

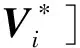
(15)

式中:Vk=[Vka,Vkb,Vkc]T;Vi=[Via,Vib,Vic]T;Pik=[Pika,Pikb,Pikc]T;Qik=[Qika,Qikb,Qikc]T;zik∈C3×3;∅表示按分量点除。下文中功率、电流、电压均为3×1维向量，阻抗均为3×3阶矩阵。

由于配电网中各节点电压一般相差很小,即|Via|≈|Vib|≈|Vic|[20],而且相角不平衡的角度α很小,一般在1°～3°以内。忽略α并且认为三相电压相等,式(15)左右两边各点乘其共轭向量可以得到:

k∈N

(16)

(17)

(18)

(19)

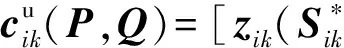
(20)

式中:⊙表示按分量点乘。

功率方程为:

(21)

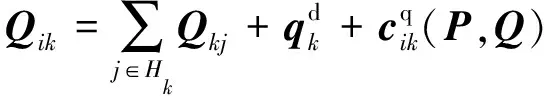
(22)

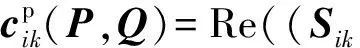
节点k的三相负荷功率为:

(23)

(24)

根节点的电压为:

UN+1=|Vs|⊙|Vs|

(25)

2 电动汽车有序充电的模型

目标函数为优化时段内,车主总的充电费用最小,如式(26)所示。

(26)

式中:ρ(t)为t时段的电价;PEVk,t和PEVm,β,t分别为第k,m辆采用三相、单相充电方式的电动汽车t时段的充电功率;下标β为接入的相别;K和M为相应电动汽车的数量;t1和tmax分别为优化的开始、结束时间;Δt为间隔时间。

采用三相充电方式的电动汽车充电功率约束[18]为:

0≤PEVk,t≤PEVk,max

(27)

(28)

式中:PEVk,a,t,PEVk,b,t,PEVk,c,t,PEVk,max分别为a,b,c相t时段的充电功率和三相充电功率最大值。

采用单相充电方式的电动汽车充电功率约束[12]为:

0≤PEVm,β,t≤PEVm,max

(29)

式中:PEVm,max为第m辆采用单相充电方式的电动汽车充电功率最大值。

采用三相、单相充电方式的电动汽车能量需求约束[18]分别为:

(30)

(31)

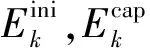
节点电压约束为:

Umin≤Un,α,t≤Umax

(32)

式中:Un,α,t,Umax,Umin分别为t时段配电网节点n的α相电压的平方及其上、下限值。

线路功率约束为:

(33)

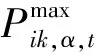
配变功率约束为:

(34)

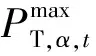
对于三相平衡配电网，整个模型的目标函数为式(26),等式约束为式(7)至式(12)、式(28)、式(30),不等式约束为式(29)、式(32)至式(34)。对于三相不平衡配电网，整个模型的目标函数为式(26),等式约束为式(16)、式(21)至式(25)、式(28)、式(30)和式(31),不等式约束为式(27)、式(29)、式(32)至式(34)。

3 求解方法

3.1 三相平衡配电网支路潮流方程的线性化

(35)

(36)

hik(P,Q)可线性化为:

(37)

式中:Pik0,Qik0,Sik0,Vi0分别为有功功率、无功功率、视在功率、电压线性化的初始点。

3.2 三相不平衡配电网支路潮流方程的线性化

1)电压方程非线性项的线性化

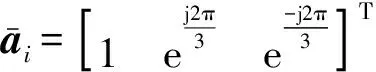
(38)

定义新的支路阻抗矩阵为:

(39)

则式(38)可改写为:

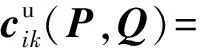
(40)

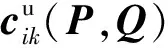
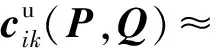
(41)

根据式(40)可得,偏导数项可表示为:

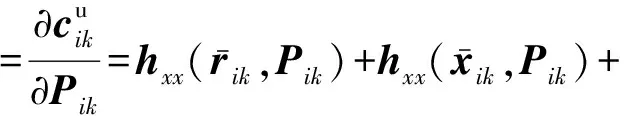
(42)

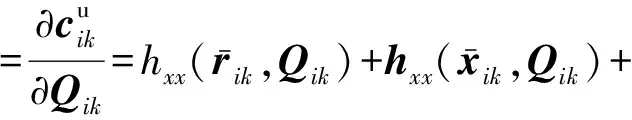
(43)

hxx(A,x)=2diag(Ax)A

(44)

hxy(A,B,x,y)=diag(By)A

(45)

2)功率方程非线性项的线性化

支路(i,k)上的功率损耗为:

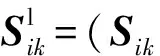
(46)

再次定义新的支路阻抗矩阵为:

(47)

根据上式可得:

(48)

(49)

因此,式(46)可改写成:

(50)

根据上式将有功与无功功率分开得到:

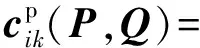
(51)

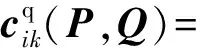
(52)

式(51)和式(52)的线性化表达式分别为:

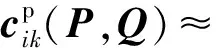
(53)

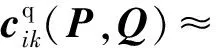
(54)

偏导数项分别为:

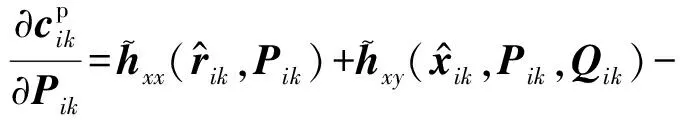
(55)

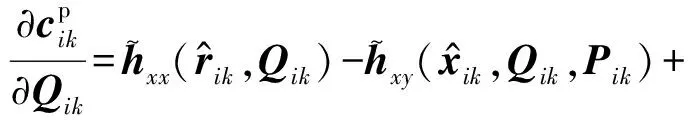
(56)

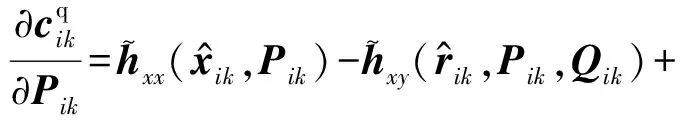
(57)

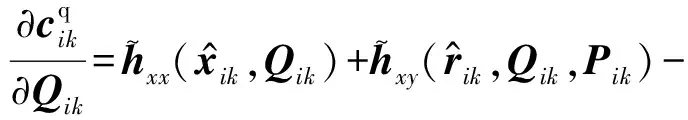
(58)

(59)

(60)

(61)

3.3 模型的快速求解方法

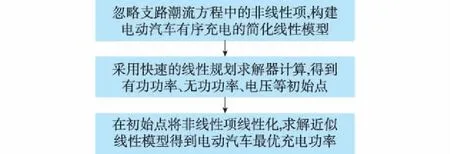
图1 模型求解方法框图Fig.1 Block diagram of model solving method

4 仿真算例

4.1 仿真算例1

1)仿真条件

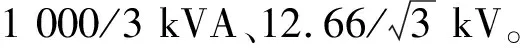
2)仿真结果

采用MATLAB线性规划函数linprog与编写非线性原对偶内点法[21]进行计算,计算机的CPU型号为intel(R) Core (TM) i3-4510,主频为3.5 GHz,RAM 32 GB。部分计算结果如表1、表2和附录A表A3所示。表中:P0,V0和P1,V1分别为求解简化线性模型得出的12:00—13:00和13:00—14:00时段的最优充电功率和电压;P2,V2和P3,V3分别为求解近似线性模型得出的12:00—13:00和13:00—14:00时段的最优充电功率和电压;P4,V4和P5,V5分别为采用原对偶内点法求解精确模型得出的12:00—13:00和13:00—14:00时段的最优充电功率和电压;V6和V7分别为将求解简化线性模型得出的最优充电功率代入潮流方程进行潮流计算得到的12:00—13:00和13:00—14:00时段的电压;V8和V9分别为将求解近似线性模型得出的最优充电功率代入潮流方程进行潮流计算得到的12:00—13:00和13:00—14:00时段的电压。本文采用前推回代潮流计算方法。

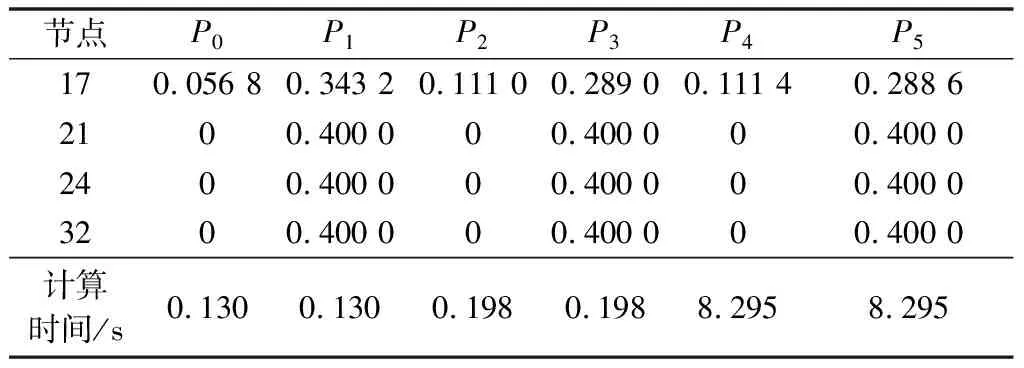
表1 不同优化算法的最优充电功率Table 1 Optimal charging power under different optimization algorithms

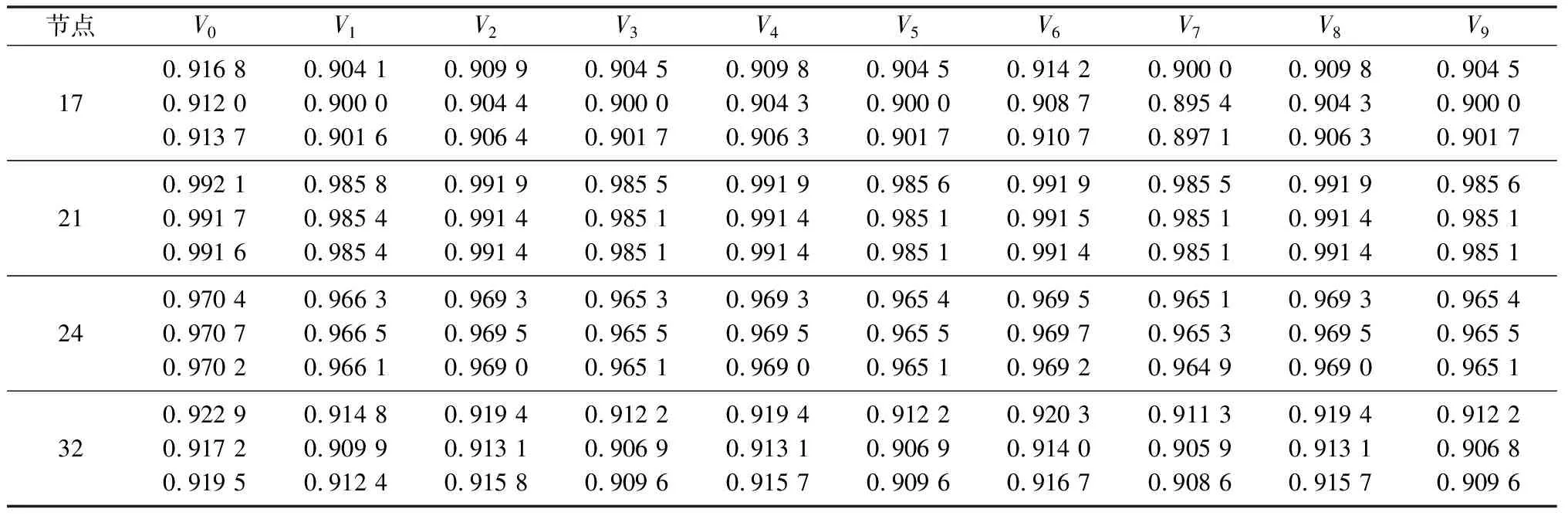
表2 不同优化算法的电压计算结果Table 2 Voltage calculation results under different optimization algorithms

从表1和表2可以看出:采用简化、近似线性模型得出的结果较接近。因此本文以求解简化线性模型得出的结果作为初始点线性化支路潮流方程非线性项精度较高。本文所提出的方法与采用精确模型的原对偶内点法对应时段电压、充电功率的优化计算结果十分接近,进一步证实本文提出的方法精度较高。而且本文方法比原对偶内点法计算速度提高了约40倍。从潮流计算的结果可以看出,采用简化线性模型得出的最优充电功率进行充电可能导致电压跌出下限(最低为0.895 4和0.897 1),而对于近似线性模型,潮流计算结果与优化结果十分接近,电压处于额定范围内。

4.2 仿真算例2

1)仿真条件

电动汽车采用单相充电以验证本文所提方法的精度。仿真系统与文献[22]中的算例2相同,分时电价为0.8,0.4元/(kW·h)。12:00—13:00时段,除配电网根节点外每个节点每相负荷为4.5 kW,13:00—14:00时段各节点负荷为12:00—13:00时段的80%。每辆电动汽车充电需求为5 kW·h,充电功率下、上限分别为0,4 kW。其他仿真条件与文献[22]中的算例2相同。

2)仿真结果

采用MATLAB线性规划函数linprog与编写非线性原对偶内点法进行计算,计算机配置同算例1。不同优化算法的仿真计算结果如附录A表A3和表A4所示。可以看出,本文所提出的方法计算结果与原对偶内点法吻合得很好,而且计算速度远远优于原对偶内点法。

4.3 仿真算例3

1)仿真条件

配电网中单相与三相充电方式并存以验证本文所提方法的精度与计算效率。仿真系统仍采用文献[22]中的算例2,从节点3,4,5,8,9,10接入的电动汽车采用三相充电方式,每相充电功率上限为4 kW,其他仿真条件与4.2.1节相同。

2)仿真结果

不同优化算法每相最优充电功率与程序计算时间如附录A表A5所示。可以看出,所提出的方法计算效率略优于算例2的只含单相充电情形,这是因为本文取三相充电方式的优化变量为A相充电功率,优化变量维数与算例2相同,等式约束只需在算例2的基础上略做修改,使得B,C相充电功率等于A相以及采用三相充电方式的优化变量各优化时段累加和乘以充电效率等于总充电需求的三分之一。即通过一些简单的数学技巧使得优化变量的维数与约束条件的数量与算例2相同。由于三相充电方式降低了配电网的三相不平衡,程序的数值稳定性更好,速度有所提高。不同优化算法电压计算结果与附录A表A4类似,受篇幅限制,不再列出。由仿真结果可以得出与算例2类似的结论,不再赘述。

3个仿真算例不同优化方法的计算时间对比图如图2所示。可以看出,本文所提出的方法总计算效率远高于原对偶内点法,略低于简化线性模型,但精度十分接近原对偶内点法。

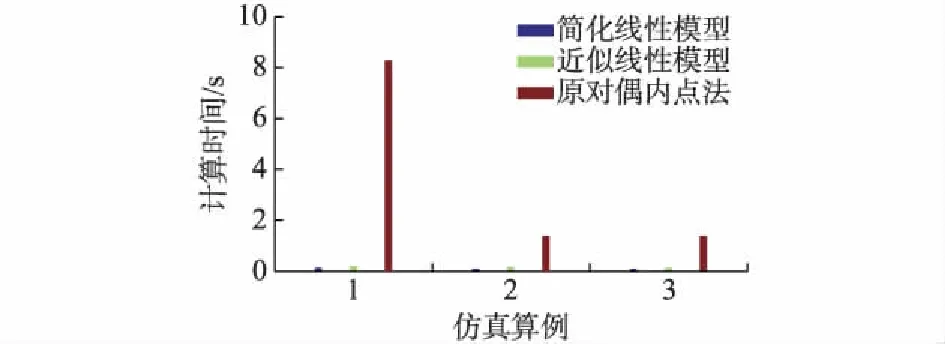
图2 不同优化算法的计算效率Fig.2 Computational efficiency of different optimization algorithms

4.4 仿真算例4

1)仿真条件

采用354节点配电网测试所提方法的性能。中压配电网为IEEE 34节点配电系统,额定相电压为13.8 kV,单线图如附录A图A3(a)所示。测试系统包含16个低压配电网,单线图如附录A图A3(b)所示,额定相电压为220 V。配变容量为250 kVA,X端分别从节点11,13,14,17,18,20,22,24至26,28至33接入中压配电网。中、低压配电网电缆的额定电流分别为200,368 A。分时电价与常规负荷水平见附录A表A6。其他仿真条件设置如下:①电压上、下限分别为1.1,0.9;②在低压配电网中每个节点均接入一个家庭用户,每个家庭用户拥有一辆电动汽车;③时段18每家每户A,B,C相常规负荷分别为0.866 6,0.800 0,0.733 4 kW,共2.4 kW,功率因数为0.95,负荷模型采用60%恒功率+40%恒阻抗模型;④每辆电动汽车电池容量为50 kW·h,充电需求为15 kW·h;⑤电动汽车均采用三相充电方式,充电功率下、上限分别为0,10 kW;⑥优化时段为时段18至次日时段8,时间间隔为1 h。

2)仿真结果

采用MATLAB调用cplex线性规划函数cplexlp进行优化计算,计算机配置同仿真算例1。优化时段内,配电网总常规负荷、采用简化、近似线性模型得出的各时段总充电负荷(分别采用蓝色、绿色、深红色柱状图表示)如附录A图A4所示。可以看出,电动汽车只在电价低谷时段4,5,6进行充电,其他时段不充电。但是求解两种模型得出的对应时段总充电功率差异显著。此三时段内时段5的总充电负荷最大,时段6次之,时段4最小。这是因为时段5电价最低,电动汽车优先在此时段充电,直至电压达到下限。时段6的电价与总常规负荷均高于时段5,故总充电负荷小于时段5。时段4的电价高于时段6,总常规负荷小于时段6,与时段5相等,但由于电动汽车充电需求已大部分由时段5和6的充电功率提供,故时段4的总充电负荷远小于时段6。

记与配电网根节点、配变低压侧相连的电缆为中、低压主电缆。优化时段内,配变、中、低压主电缆的负载率如附录A图A5所示。从图A5(a)(c)(d)可以看出,在电价高峰时,负载率较小,在电价低谷时,负载率较高,但均未超过90%。配电网设备的容量足以接纳充电负荷。另一方面,可以看出,两种模型求解得到的支路功率十分接近,故求解简化线性模型得出的支路功率作为支路潮流方程非线性项线性化的初始点是合理的。

求解简化及近似线性模型得出的各时段最小电压如附录A图A6(a)所示。比照图A4可以看出:在总负荷较小时段,最小电压较大;在总负荷较大时段,最小电压较小。最小电压均处于额定范围内。然而,根据求解两种模型得出的最优充电功率进行潮流计算得到的各时段最小电压如附录A图A6(b)所示。可以看出,由于简化模型忽略了网损,导致潮流计算的最小节点电压跌至0.865 1,0.865 9,因此采用简化模型得到的最优充电功率,无法保证满足节点电压约束,可能是不可行解。而根据求解近似线性模型得出的最优充电功率进行潮流计算,时段5和6的最小电压分别为0.896 3和0.897 5,近似满足节点电压约束,这是因为线性化方法以简化线性模型的求解结果作为初始点,具有很高的精度。

充电地点距离配电网根节点最近、远的电动汽车最优充电功率如附录A图A7所示。可以看出,在电价低谷时(时段4,5,6),充电功率较大,甚至达到最大值。在电价较高时(时段18至次日时段3,以及时段7)电动汽车充电功率为零。由于处于配电网前端的电动汽车已在最低电价时段5和6以最大功率充电,处于配电网末端的电动汽车只能在时段4,而不是时段5和6,以最大功率充电以避免电压跌出下限。

3)与其他方法的比较

由附录A图A4至图A7可以看出,所有电动汽车只在时段4至6充电,其他时段不充电。因此,在图1中的第三步,可将优化时段进一步缩短为时段4至6。大大提高计算速度。本文优化结果与文献[15]优化结果的对比如表3所示。可以看出,本文方法的计算速度远优于文献[15]。这是因为本文构建的模型基于支路潮流方程,优化变量不包含节点电压的相角与支路电流。而文献[15]的方法采用直角坐标下的电流型潮流方程,支路电流约束线性化十分复杂,引入了过多的变量与约束条件,为本文的十几倍;电压约束数量为本文的5倍,大大增加了计算时间。而且引入了离散变量使得求解问题是非凸的,大大增加了优化计算时间。

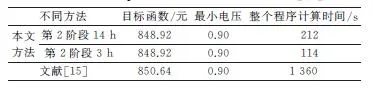
表3 与文献[15]的对比结果Table 3 Comparison results with reference [15]

5 结语

本文推导了三相平衡与不平衡配电网的支路潮流方程,提出了将方程非线性项线性化的方法。构建了以车主总充电费用最小为目标函数,节点电压、支路功率、电动汽车充电功率为不等式约束,支路潮流方程、充电需求为等式约束的电动汽车有序充电的模型。提出了采用二阶段线性规划进行求解的方法。第1阶段线性规划采用忽略支路潮流方程非线性项的简化线性方程求取支路有功、无功功率、节点电压,作为支路潮流方程非线性项线性化的初始点。第2阶段线性规划采用近似线性模型计算最优充电功率,保证了算法的精度与快速性。

以3个仿真算例表明,所提方法精度高,计算速度快,能够节省车主费用,保证配电网的安全运行,具有极高的实际应用价值。采用354节点配电网与文献[15]的方法进行了对比,计算结果表明本文方法大大提高了计算速度。本文所提出的方法同样适用于其他目标函数如网损或配电网运营商总购电费用最小等。

值得指出的是，本文方法计及了线路阻抗参数的不对称以及负荷的三相不平衡,但是没有计及节点电压的三相不平衡度约束。如何基于支路潮流方程构建计及节点电压三相不平衡度约束的电动汽车有序充电模型并提出线性化方法提高计算速度是值得研究的方向。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参考文献

[1] 陶顺,肖湘宁,彭骋.有源智能配电网[M].北京:中国电力出版社,2012.

[2] 程杉,王贤宁,冯毅煁.电动汽车充电站有序充电调度的分散式优化[J].电力系统自动化,2018,42(1):39-46.DOI:10.7500/AEPS20170630001.

CHENG Shan, WANG Xianning, FENG Yichen. Decentralized optimization of ordered charging scheduling in electric vehicle charging station[J]. Automation of Electric Power Systems, 2018, 42(1): 39-46. DOI: 10.7500/AEPS20170630001.

[3] 王锡凡,邵成成,王秀丽,等.电动汽车充电负荷与调度控制策略综述[J].中国电机工程学报,2013,33(1):1-10.

WANG Xifan, SHAO Chengcheng, WANG Xiuli, et al. Survey of electric vehicle charging load and dispatch control strategies[J]. Proceedings of the CSEE, 2013, 33(1): 1-10.

[4] SINGH M, KUMAR P, KAR I. Implementation of vehicle to grid infrastructure using fuzzy logic controller[J]. IEEE Transactions on Smart Grid, 2012, 3(1):565-577.

[5] 吕仁周,白晓清,李佩杰,等.基于交替方向乘子法的电动汽车分散式充电控制[J].电力系统自动化,2016,40(16):56-63.DOI:10.7500/AEPS20150731006.

LYU Renzhou, BAI Xiaoqing, LI Peijie, et al. Decentralized charging control of electric vehicles based on alternate direction method of multiplier[J]. Automation of Electric Power Systems, 2016, 40(16): 56-63. DOI: 10.7500/AEPS20150731006.

[6] BEAUDE O, HE Yujun, HENNEBEL M. Introducing decentralized EV charging coordination for the voltage regulation[C]// 4th IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), October 6-9, 2013, Copenhagen: 1-5.

[7] DEILAMI S, MASOUM A S, MOSES P S, et al. Real time coordination of plug in electric vehicle charging in smart grids to minimize power losses and improve voltage profile[J]. IEEE Transactions on Smart Grid, 2011, 3(2): 456-467.

[8] MASOUM A S, DEILAMI S, MOSES P S, et al. Smart load management of plug-in electric vehicles in distribution and residential networks with charging stations for peak shaving and loss minimization considering voltage regulation[J]. IET Generation, Transmission and Distribution, 2011, 5(8): 877-888.

[9] 李惠玲,白晓民,谭闻,等.电动汽车入网技术在配电网的应用研究[J].中国电机工程学报,2012,32(增刊):22-27.

LI Huiling, BAI Xiaomin, TAN Wen, et al. Application of vehicle to grid to the distribution grid[J]. Proceedings of the CSEE, 2012, 32 (Supplement): 22-27.

[10] 孙近文,万云飞,郑培文,等.基于需求侧管理的电动汽车有序充放电策略[J].电工技术学报,2014,29(8):64-69.

SUN Jinwen, WAN Yunfei, ZHENG Peiwen, et al. Coordinated charging and discharging strategy for electric vehicles based on demand side management[J]. Transactions of China Electrotechnical Society, 2014, 29(8): 64-69.

[11] 占恺峤,宋永华,胡泽春,等.以降损为目标的电动汽车有序充电优化[J].中国电机工程学报,2012,32(31):11-18.

ZHAN Kaiqiao, SONG Yonghua, HU Zechun, et al. Coordination of electric vehicle charging to minimize active power losses[J]. Proceedings of the CSEE, 2012, 32(31): 11-18.

[12] CLEMENT-NYNS K, HAESEN E, DRIESEN J. The impact of charging plug in hybrid electric vehicles on a residential distribution grid[J]. IEEE Transactions on Power Systems, 2010, 25(1): 371-380.

[13] RICHARDSON P, FLYNN D, KEANE A. Optimal charging of electric vehicles in low voltage distribution systems[J]. IEEE Transactions on Power Systems, 2012, 27(1): 268-279.

[14] RICHARDSON P, FLYNN D, KEANE A. Local versus centralized charging strategies for electric vehicles in low voltage distribution systems[J]. IEEE Transactions on Smart Grid, 2012, 3(2): 1020-1028.

[15] FRANCO J F, RIDER M J, ROMERO R. A mixed integer linear programming model for the electric vehicle charging coordination problem in unbalanced electrical distribution systems[J]. IEEE Transactions on Smart Grid, 2015, 6(5): 2200-2210.

[16] HE Yifeng, VENKATESH B, GUAN Ling. Optimal scheduling for charging and discharging of electric vehicles[J]. IEEE Transactions on Smart Grid, 2012, 3(3): 1095-1105.

[17] HU Junjie, YOU Shi, LIND M, et al. Coordinated charging of electric vehicles for congestion prevention in the distribution grid[J]. IEEE Transactions on Smart Grid, 2014, 5(2): 703-711.

[18] WECKX S, DRIESEN J. Load balancing with EV chargers and PV inverters in unbalanced distribution grids[J]. IEEE Transactions on Sustainable Energy, 2015, 6(2): 635-643.

[19] SORTOMME E, HINDI M M, PHERSON S D J, et al. Coordinated charging of plug in hybrid electric vehicles to minimize distribution system losses[J]. IEEE Transactions on Smart Grid, 2011, 2(1): 198-205.

[21] ZHANG Jian, HE Yigang, CUI Mingjian, et al. Primal dual interior point dynamic programming for coordinated charging of electric vehicles[J]. Journal of Modern Power Systems and Clean Energy, 2017, 5(6): 1004-1015.

[22] ZHANG J, CUI M, FANG H, et al. Smart charging of EVs in residential distribution systems using the extended iterative method[J]. Energies, 2016, 9(12): 1-22.