基于电磁舵机的地磁抗干扰算法研究

谢 峰， 曹红松， 张晓东， 杨鹏飞， 刘 胜， 张 亨

(1. 中北大学 弹箭模拟仿真中心， 山西 太原 030051； 2. 长江电工工业有限公司弹箭开发中心， 重庆 401336)

常规弹药制导化已经成为趋势， 通过一些简易控制机构实现对弹丸的控制， 可以达到更高的射击精度. 目前主要存在脉冲控制、 阻尼环修正、 气动舵控制等几种简易控制方法[1]实现对弹道的修正， 在控制过程中， 需要准确地获取弹丸的滚转角信息， 地磁测量滚转角具有较高的精度， 在旋转弹的制导控制中被广泛应用.

本文利用气动舵对某型火箭弹进行二维简易控制， 依据地磁数据进行弹丸飞行姿态的获取， 主要分析了电磁舵机对地磁传感器的干扰机理及对地磁姿态测试的影响， 并提出了相应的电磁隔离方法和数字滤波器， 实现弹丸姿态的准确计算和飞行弹道的实时修正.

1 地磁测量滚转角原理

旋转火箭弹的制导控制过程中， 滚转角的获取至关重要， 地磁因为其无源、 无辐射、 全天候、 全区域及误差不累计等优良特性， 常用于弹丸滚转角的测量[2]. 对于近距离炮弹而言， 可以假设弹丸在全弹道的飞行过程中地磁值与发射点地磁值一样. 将两轴磁强计固连于弹体截面， 分别探测弹体截面上两垂直方向上的地磁Hby,Hbz， 根据弹丸的地理位置， 计算得出当地地磁场矢量， 由弹体坐标系与发射坐标系的转换关系， 可以得出弹体界面上两轴的地磁量为

(1)

以此量作为基准量计算基准角γ基， 结合磁强计两轴输出， 可以得到弹丸滚转角随着弹丸飞行轨迹的变化， 使得地磁矢量在弹体截面的分量会发生变化， 此时应不断更新α和β. 图 1 为两轴地磁测量滚转角原理图.

图 1 两轴地磁测量滚转角原理图Fig.1 Two axis geomagnetic measurement roll angle principle diagram

(2)

2 舵机干扰机理分析

电磁舵机常作为制导火箭弹的二维修正执行机构， 但是由于电动舵机的运行是依靠内部磁场完成的[3,4]， 在与地磁测姿硬件系统距离一定范围内， 会影响磁强计测量的准确性， 图 2 为舵机工作前后地磁变化曲线.

图 2 舵机工作前后地磁变化曲线Fig.2 Geomagnetic variation curve before and after actuator work

图 3 电动舵机干扰地磁示意图Fig.3 The diagram of geomagnetic disturbance

由于舵机是依靠内部线圈施加电流产生磁力， 驱动舵片的偏转， 地磁的干扰变化规律会跟随舵机偏转[5,6]. 当舵机开始工作， 舵机内部会产生磁场， 该磁场不仅会对驱动舵片偏转， 还会在地磁电路板平面产生与舵机驱动地磁方向相反的干扰地磁， 如图 3 所示. 当地磁传感器的两轴方向与舵机产生的干扰地磁方向相反或相同时， 磁强计感知的干扰地磁量就会增大， 即Y轴干扰最大； 当地磁探测轴与干扰地磁方向垂直时， 磁强计感知的干扰地磁会减少， 如图 3，Z轴干扰最小.

由于地磁芯片正在安装过程中会存在误差， 即使干扰地磁方向与磁轴方向垂直， 也同样会受到舵机电磁的干扰， 本文将地磁测姿系统与舵机在地面进行了相关实验， 根据不同安装位置， 测量舵机偏转对磁强计测量的影响， 测试结果如图 4 所示.

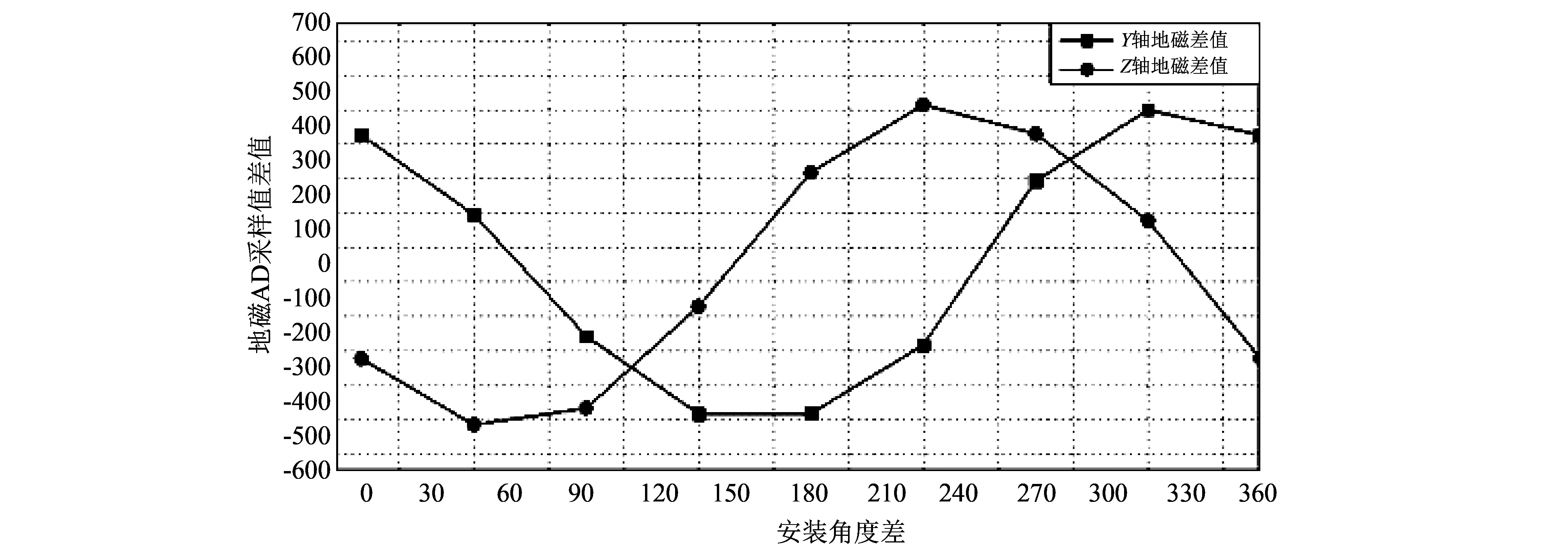
图 4 不同安装角度下Y, Z两轴地磁测量误差Fig.4 The magnetic measurement error of Y and Z in different installation angles

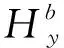
从图 4 中可知， 即使选取最佳安装位置， 电磁舵机仍然会对地磁测量产生一定的误差. 在飞行控制过程中舵机按照一定的周期进行偏转， 产生的干扰也具有固定的频率， 假设舵机偏转一次的时间为30 ms， 则干扰信号的频率约为33 Hz. 对于已知频率的干扰信号， 本文设计了相应的滤波器.

3 数字低通滤波器的设计

为了完成舵机在射程和高度方向上的修正， 在弹丸转动一圈的过程中， 一般要求舵片完成2或4次偏转， 即舵机的偏转频率至少是2～4倍. 本文研究的火箭弹在飞行稳定过程中的滚转角速率达到5 rad/s， 转动频率为5 Hz， 此时舵片偏转频率为20 Hz. 可以设置低通滤波器完成对电磁干扰的消除.

巴特沃斯滤波器是一种具有最大平坦幅度响应的滤波器， 具有结构简单、 运算速度高、 占用内存少等优点[7]， 与贝塞尔、 切比雪夫滤波器相比， 巴特沃斯滤波器在线性相位、 衰减斜率和负载特性3个方面具有特性均衡的优点[8].

无线冲击响应滤波器(IIR)的系统函数为

(3)

式中：N为滤波器的阶数，N阶巴特沃斯低通滤波器的振幅和频率关系为

(4)

式中：ωc为通带宽度即截止频率， 阶数N主要影响幅度特性下降的速度， 对于模拟低通滤波器， 其设计指标有ap，ωp，as和ωs. 其中ωp和ωs分别称为通带截止频率和阻带截止频率，ap是通带中的最大衰减系数，as是阻带的最小衰减系数. 根据特性函数式(4)可得

(5)

整理可得

(6)

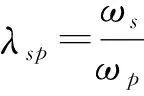
(7)

弹丸的二维修正执行时间一般选择在飞行弹道的下降段， 此过程弹丸的滚转角速率稳定在4～8 rad/s， 此时可以选择低通滤波器的技术指标如式(8)所示， 可以得到N=4， 完成四阶巴特沃斯低通滤波器的设计.

ωp=10 Hz,ωs=15 Hz,αp=1 dB,αs=8 dB.

(8)

地磁数据在经过巴特沃斯低通滤波器滤波之后， 依然会存在干扰. 采用椭圆拟合法[9,10]可以有效地消除地磁干扰. 将弹丸旋转一周记录下磁强计两轴输出的最大值和最小值(Hymax,Hymin,Hzmax,Hzmin)， 计算两轴的平移因子和伸缩因子.

伸缩因子

(9)

平移因子

(10)

原始地磁Hy和Hz可以通过平移和伸缩变换得到校正值

(11)

4 实验结果与分析

将地磁滚转测量系统与舵机安装在两轴转台上， 并进行如下实验：

1) 将地磁滚转测量系统单独置于两轴转台上， 设置不同转速， 分别记录双轴地磁及滚转角变化曲线， 如图 5 和图 6 所示.

不同的转速下， 分析滚转角的绝对误差(取固定时间段内滚转角误差的平均值)， 得到不同转速下的滚转角绝对误差如表 1 所示. 由表1可知地磁测量滚转角的误差在1°以下， 误差在可接受范围， 证明了系统的稳定性和算法的可行性， 为滤波算法的验证提供了基础.

表 1 不同转速下滚转角误差

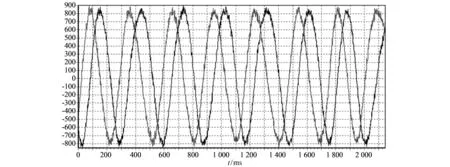
图 5 双轴地磁变化曲线Fig.5 Biaxial geomagnetic variation curve

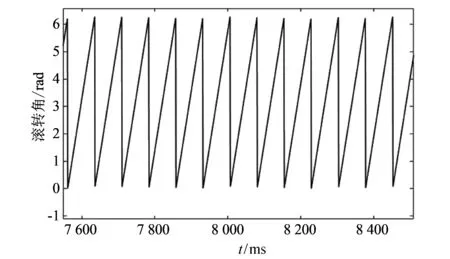
图 6 地磁测量滚转角变化曲线Fig.6 Variation curve of ground magnetic measurement roll angle

2) 控制转台以固定转速4 rad/s 转动， 分别记录舵机工作前后地磁姿态测量系统输出的滚转角变化曲线， 如图 7 所示. 从图 7 中可以看出， 当舵片发生偏转时， 滚转角的测量曲线不是一条直线， 会出现4°左右的误差， 而且最大值可达到10°以上， 很难满足控制要求.

3) 控制转台以4 rad/s的转速运行， 控制舵机在一周内偏转4次， 模拟实际飞行控制过程， 得出滚转相位差在使用滤波器前后的相位差曲线， 如图 8 所示. 从图 8 中可以看出， 在滤波后滚转相位角的误差最大可达到3°左右， 相较于滤波前的最大10°有了极大的提高.

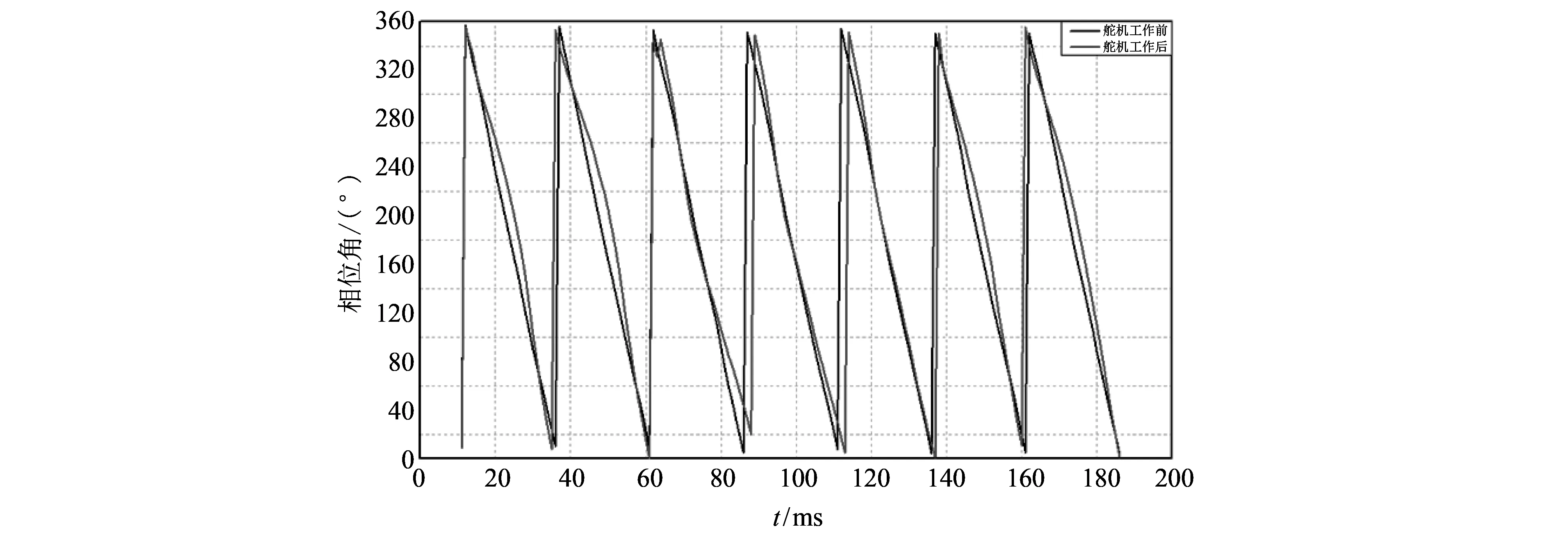
图 7 舵机工作前后滚转角变化曲线Fig.7 The rolling angle variation curve of actuator before and after working

图 8 滤波前后滚转相位差曲线Fig.8 Before and after the filter roll the phase difference curve

5 结 论

本文介绍了双轴地磁测量滚转角的原理， 针对电磁舵机对磁强计测量的干扰， 分析了影响干扰强度的因素， 提出了最佳安装角度， 设计了巴特沃斯低通数字滤波器. 基于双轴转台， 测试了滚转角测量系统的稳定性及精度， 对比了经过滤波器前后的滚转角测量误差. 综合实验结果可知： 本文提出的抗干扰措施能够有效地减少舵机电磁对滚转角的影响， 对其它舵机抗干扰问题的解决具有一定的参考性.

参考文献：

[1] 赵金强， 龙飞， 孙航. 弹道修正弹综述[J]. 制导与引信， 2005， 26(4)： 16-19.

Zhao Jinqiang, Long Fei, Sun Hang. Overview of trajectory correction missiles[J]. Guidance and Fuze, 2005, 26(4)： 16-19. (in Chinese)

[2] Du Guangtao, Chen Xiaodong. MEMs magnetometer based on magnetorheological elastomer[J]. Measurement, 2012(45)： 54-58.

[3] 黄建勋. 弹道修正弹电磁舵机系统设计[D]. 南京： 南京理工大学， 2009.

[4] 赵雨东， 吴亚楠， 付雨民， 等. 发动机电磁气门驱动设计试验与仿真[J]. 清华大学学报(自然科学版)， 2003(5)： 698-701.

Zhao Yudong, Wu Yanan, Fu Yumin, et al. Simulation and testing of electromagnetic valve actuation forengines[J]. Journal of Tsinghua University(Science and Technology), 2003(5)： 698-701. (in Chinese)

[5] 刘建敬， 张合， 丁立波. 一种地磁传感器对电磁舵机的抗干扰方法[J]. 测试技术学报， 2012， 26(3)： 272-276.

Liu Jianjing, Zhang He, Ding Libo. An anti-jamming method of geomagnetic sensor to electromagnetic actuator[J]. Journal of Test and Measurement Technology, 2012, 26(3)： 272-276. (in Chinese)

[6] 高峰， 张合. 基于基准角和补偿角的常规弹药滚转角磁探测算法研究[J]. 探测与控制学报， 2008, 30(5)： 11-15.

Gao Feng, Zhang He. Algorithm of roll angle determination of conventional ammunitions based on benchmark angle and compensation angle[J]. Tournal of Detection and Control, 2008, 30(5)： 11-15. (in Chinese)

[7] 甘明刚， 潘凤， 蔡涛. 基于协调粒子群算法的无线冲激响应滤波器优化设计[J]. 兵工学报， 2010， 31(10)： 1398-1402.

Gan Minggang, Pan Feng, Cai Tao. Optimization design of wireless impulse response filter based oncoordinated particle swarm optimization[J]. Journal of military engineering, 2010, 31(10) ： 1398-1402. (in Chinese)

[8] 白松， 曹红松， 张宪国. 弹载地磁测量系统的抗干扰设计[J]. 传感技术学报， 2014， 27(7)： 928-932.

Bai Song, Cao Hongsong, Zhang Xianguo. Anti-interference design of the geomagnetic measurement system[J]. Journal of Sensing Technology, 2014, 27(7)： 928-932. (in Chinese)

[9] 史连艳， 宋文渊. 基于旋转因子的磁传感器误差补偿改进椭圆法[J]. 探测与控制学报， 2010， 32(2)： 5-8.

Shi Lianyan, Song Wenyuan. An improved elliptical method for magnetic sensor error compensation based on rotation factor[J]. Journal of Detection and Control， 2010, 32(2)： 5-8. (in Chinese)

[10] 赵鑫炉， 张晓明， 白渚铨. 基于磁阻传感器的航姿测量系统罗差补偿技术研究[J]. 传感技术学， 2006， 26(11)： 1504-1507.

Zhao Xinlu, Zhang Xiaoming, Bai Zhuquan. Research on the compensation technology of compass for the measurement system based on magnetoresistance sensor[J]. Sensing Technology, 2006, 26(11) ： 1504-1507. (in Chinese)