零售商长期后悔规避的供应链网络动态均衡

徐明姣，周 岩

(青岛大学管理科学与工程系，山东 青岛 266071)

1 引言

后悔是与日常决策、认知方式和情绪体验等密切相关的一种消极情感，当个体认识到或者想象出如果之前能够采取其他的决策将产生更有利的结果，则产生后悔情感。

自Loomes和Sugden[1]提出后悔理论，后悔理论的应用非常广泛。Perakis和Roels[2]研究了后悔行为对报童模型的影响。Ayvaz-Cavdaroglu等[3]研究了最小后悔感知下的收益管理问题。Fujii等[4]研究了后悔和兴奋如何影响人们对混合保险的选择问题。Chassein和Goerigk[5]通过分析最小最大后悔目标函数，提出并解决了无约束组合优化问题。Gilbert和Spanjaard[6]通过双重oracle算法实现最短路径的最小最大后悔优化问题。Skelton和Allwood[7]研究结果表明绝大多数成年人会对过去的购买感到后悔，且后悔购买的倾向随着年龄而减少。Wang Jiamin和Xiao Baichun[8]将后悔理论应用于易腐产品的价格管理。国内，饶俪琳等[9]结合不同后悔模型总结了后悔对决策行为的影响。张晓等[10]利用后悔理论对风险型多属性决策进行了分析。袁媛等[11]提出了考虑后悔规避的风险决策方法。韩菁等[12]运用后悔理论解决了混合型多属性案例问题。于超和樊治平[13]应用后悔理论解决风险投资项目的排序问题。 张华民等[14]研究了零售商考虑后悔准则的供应链均衡决策问题。高鹏等[15]分析了后悔预期对供应链权力结构的影响。李梦和黄海军[16]研究了后悔行为在用户路径选择问题的应用。

另一方面，将后悔效用根据时间因素，分成短期后悔、长期后悔[17]。Abendroth和Kristin[18]发现后悔效用随着时间会发生变化。国内，张结海[19]提出了三种模型来解释短期后悔和长期后悔的不同。

Nagurney等[20]运用变分不等式研究供应链网络静态均衡问题，该问题成为研究热点。Dong等[21]研究了不确定性需求的供应链网络静态均衡。随着供应链管理理论的发展，上下游企业之间的交易关系常常会呈现出长期性和动态性，所以供应链网络动态均衡模型更好的描述现实中决策的动态变化关系。Daniele[22]运用了进化变分不等式，研究了产品价格和运价随时间变化的供应链网络动态均衡。Nagurney等[23]研究了时间敏感市场的供应链网络动态均衡。Feng Zhifang等[24]探讨了季节性不确定需求下的闭环供应链网络动态均衡。国内，孙嘉轶等[25]研究了闭环供应链网络的动态博弈均衡问题，张桂涛等[26]探讨了具有损失规避的供应链网络动态均衡问题。

综上可知，目前应用后悔理论研究的问题有报童问题、保险问题、风险决策等问题；鲜有文献分析决策者的长期后悔规避行为对供应链网络均衡决策的影响。然而现实中，供应链网络上下游企业之间的交易呈现长期性和动态性，决策者的长期后悔规避行为会对网络各决策者的均衡生产量、订购量、利润和效用产生如何影响？

基于以上分析和结果，本文将零售商长期后悔规避效用应用于供应链网络动态均衡模型中。在需求随时间变化的动态供应链网络中，分析零售商长期后悔规避行为对供应链网络动态均衡的影响。通过对零售商长期后悔规避心理变化的研究，得出研究结果，指导供应链网络中企业，在动态变化的市场需求下做出考虑长期后悔规避的最优决策。

2 供应链网络的均衡条件

2.1 问题描述

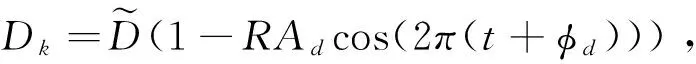
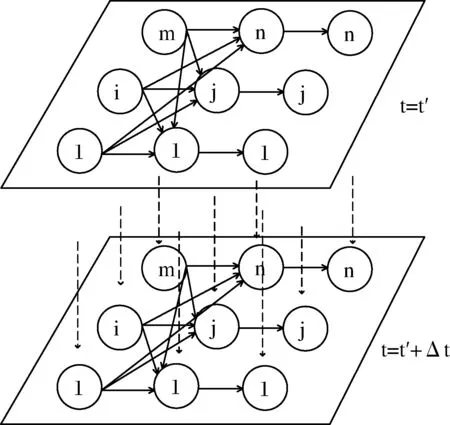
图1 供应链网络结构图

在[0,T]内任意t时刻，m个相互竞争的制造商生产同质产品销售给零售商，制造商是后悔中性的，决策目标为时间[0,T]内总利润最大。n个相互竞争的零售商从m个制造商处订购产品，满足需求市场的随机需求。由于零售商面临随机需求，因此任意t时刻存在供不应求的缺货风险和供大于求的滞销风险，零售商会根据当前获利与最优获利进行比较，对其决策结果产生后悔规避心理，因此假设零售商是后悔规避的，且其后悔规避程度会随着时间变化。零售商的决策目标为时间[0,T]内考虑长期后悔规避的总效用最大。

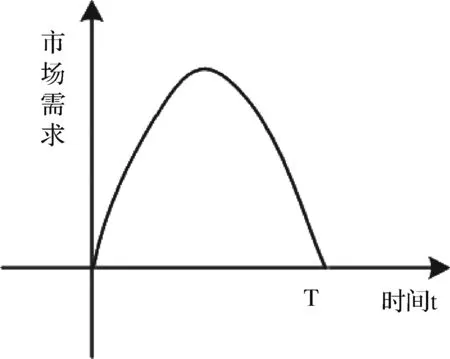
图2 市场需求曲线

本文所需的决策变量、费用函数及其他参数如下所示：

(1)决策变量

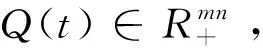
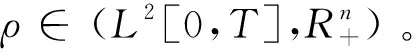
(2)费用函数、参数

fi(Q(t))表示t时刻制造商i生产费用函数,包括采购费用和加工费用；

cij(qij(t))表示t时刻制造商i与零售商j交易费用函数；

cj(Q(t))表示t时刻零售商j展销商品的费用函数。

为了表示多个制造商之间、多个零售商之间的竞争关系，假设fi(Q(t))，cj(Q(t))是所有交易量的函数。为了均衡解的存在性，假设所有费用函数为连续可微的凸函数。

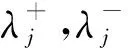
k1j,k2j分别为零售商j的存货、缺货后悔系数。

2.2 制造商层均衡模型

m个相互竞争的制造商是后悔中性的，以[0,T]内利润最大化为目标，其中制造商i的利润为销售产品给n个零售商的收入扣除所有费用，包括生产费用、交易费用。 因此，在t时刻，制造商i利润最大化模型为：

s.t.qij(t)≥0,t∈[0,T],∀j

(1)

其中ρij(t)为内生价格变量。

性质1所有的制造商之间是Nash非合作竞争的，且由费用函数的假设，所有制造商的均衡决策可用如下进化变分不等式[24]来表示：确定

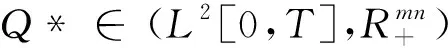
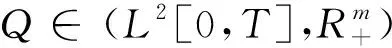
(2)

(3)

即制造商i和零售商j在交易时产品的内生价格变量为

(4)

2.3 考虑长期后悔规避的零售商层均衡模型

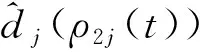
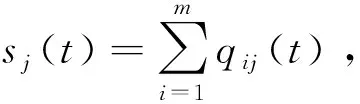
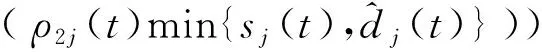
(5)

零售商j不仅要考虑其利润，还要考虑其后悔效用。根据后悔理论[1]，零售商j后悔效用包括两部分：当前决策利润函数和后悔函数，则在t时刻零售商j考虑后悔规避的效用函数为：

(6)

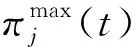
(7)

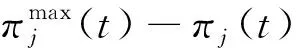
g(x)=1-e-δ(t)x

(8)

其中δ(t)为在t时刻零售商的后悔规避程度。由于零售商的后悔规避程度随着时间的推移而变化，即后悔规避系数δ(t)是关于时间t的函数，所以当零售商的后悔规避程度呈上升趋势时，假设δ(t)=A*t(情形1)，当后悔规避程度保持不变时，假设δ(t)=A(情形2)，当后悔规避程度呈下降趋势时，假设δ(t)=A*(T-t)(情形3)。

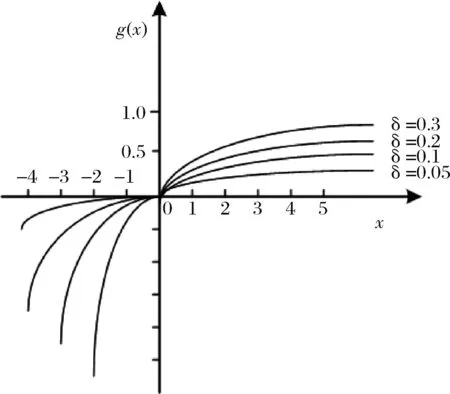
图3 后悔-欣喜函数

根据式(5)和式(7)得到零售商j存货后悔值为：

(9)

零售商j的缺货后悔值为：

(10)

则在t时刻零售商j考虑后悔规避的效用函数为：

(11)

进一步得到零售商j考虑后悔规避的期望效用最大化模型：

fj(x,ρ2j(t))dx

s.t.qij(t)≥0,t∈[0,T], ∀i

(12)

证明：由式(12)，求E(Uj(t))关于qij(t)一阶、二阶导数分别为：

(13)

(14)

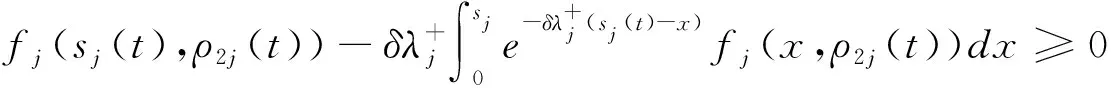
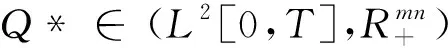
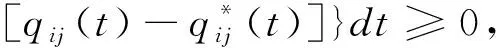
(15)

2.4 需求市场层均衡模型

需求市场j供需均衡条件可表示为如下互补条件[21]，即：

(16)

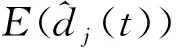
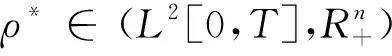
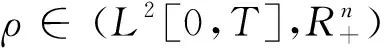
(17)

3 零售商考虑长期后悔的供应链网络动态均衡模型

整个供应链网络动态均衡为制造商层、零售商层以及需求市场层都达到均衡，即同时满足性质1、性质2和性质3，根据进化变分不等式的可加性，得到零售商考虑长期后悔规避的供应链网络动态均衡。

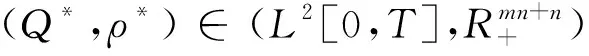
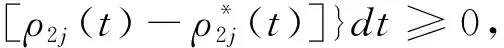
(18)

4 数值算例

4.1 算例1

在数值算例中，考虑由2个制造商(i=1,2)和2个零售商(j=1,2)构成的供应链网络，在[0,1]时间内，分别在三种零售商长期后悔规避情形，分析零售商长期后悔规避行为对均衡订购量、利润、效用、后悔值、市场价格的影响。

需要的费用函数(参考Dong等[21])如下：

制造商的生产费用：

f1(Q(t))=2.5(q11(t)+q12(t))2+(q11(t)+q12(t))(q21(t)+q22(t))+2(q11(t)+q12(t))，

f2(Q(t))=2.5(q21(t)+q22(t))2+(q11(t)+q12(t))(q21(t)+q22(t))+2(q21(t)+q22(t))

制造商的交易费用：

零售商展销费用为：

fj(x,ρ2j(t))=ρ2j(t)/bj,

Pj(x,ρ2j(t))=xρ2j(t)/bj,

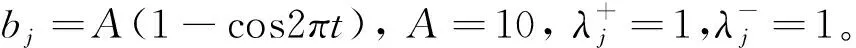
算例采用了修正投影算法[28]，通过Matlab编写程序得出结果，迭代步长0.01，收敛标准为两次迭代的差的绝对值不超过10-6。

具体分为3种情形，在[0,1]时间内，分析零售商后悔规避程度的变化对对均衡订购量、利润、效用、后悔值、市场价格的影响：

情形1: 在[0,1]时间内，当零售商的后悔规避程度呈上升趋势时，即δ(t)=A*t，零售商对自己所做的决定是越来越后悔的。

情形2：在[0,1]时间内，当零售商的后悔规避程度保持不变时，即δ(t)=A，从长期看，零售商对自己所做的决定的后悔程度是不变的。

情形3：在[0,1]时间内，当零售商的后悔规避程度呈下降趋势时，即δ(t)=A*(T-t)，零售商对自己所做的决定感到后悔程度是越来越小的。

上述三种情形，分别求解变分不等式(18)得到数值结果。比较分析零售商后悔规避程度变化的三种情形对均衡订购量、制造商的利润、零售商的利润、后悔值、效用、均衡市场价格的影响，分别如图4-9所示。

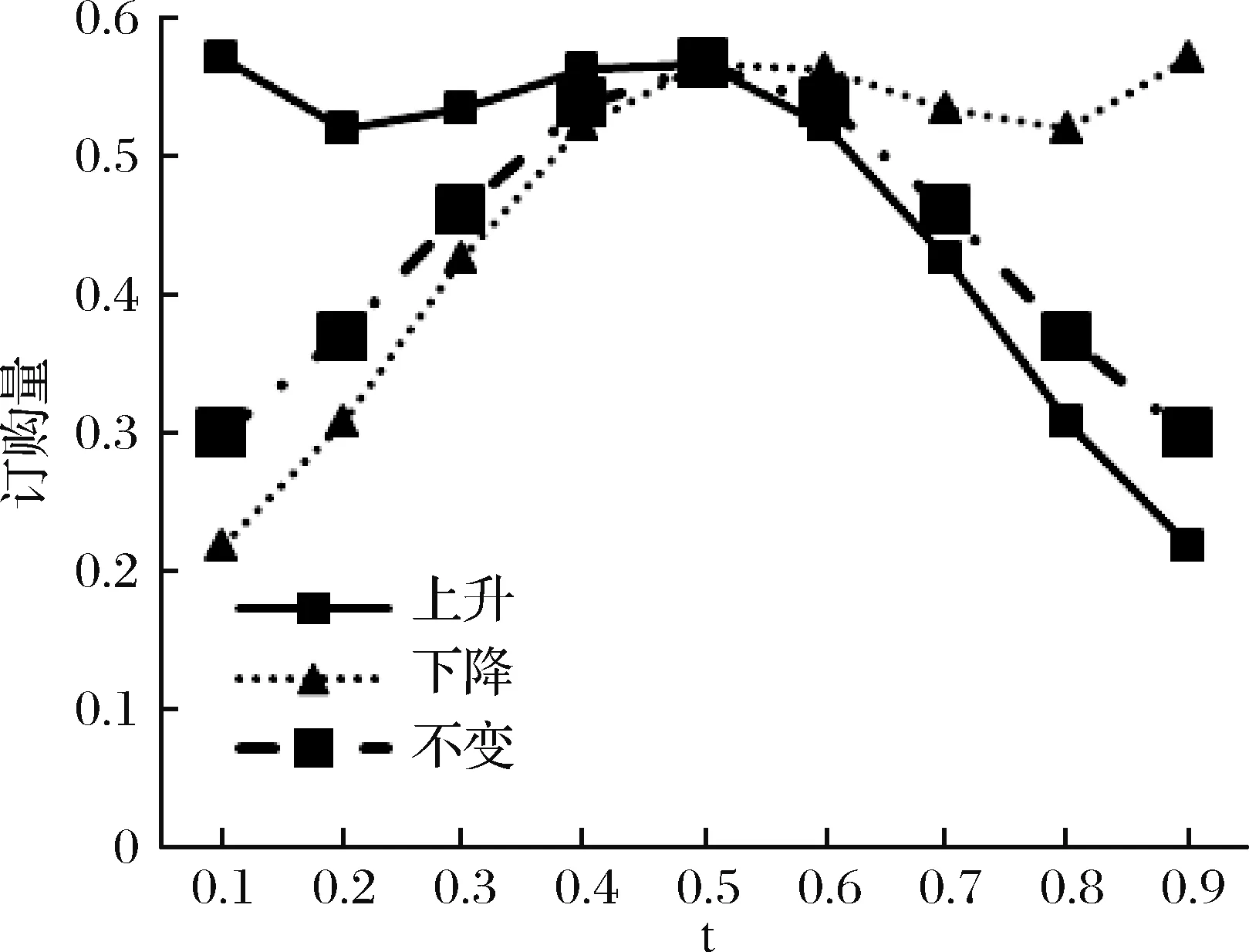
图4 三种情形下均衡订购量的比较分析图

从图4看出，从长期来看，(1)当零售商的后悔规避程度保持不变时，受季节性市场需求的影响，零售商与制造商间的均衡订购量会随着需求的变化而变化，即后悔规避对均衡订购量的影响不明显； (2)当零售商的后悔规避程度随时间逐渐增大时，此时对均衡订购量产生很大的影响，零售商越后悔，订购量会减少；(3)当零售商的后悔规避程度随时间逐渐减少时，此时零售商会做出相反的决定，订购量会逐渐增加。

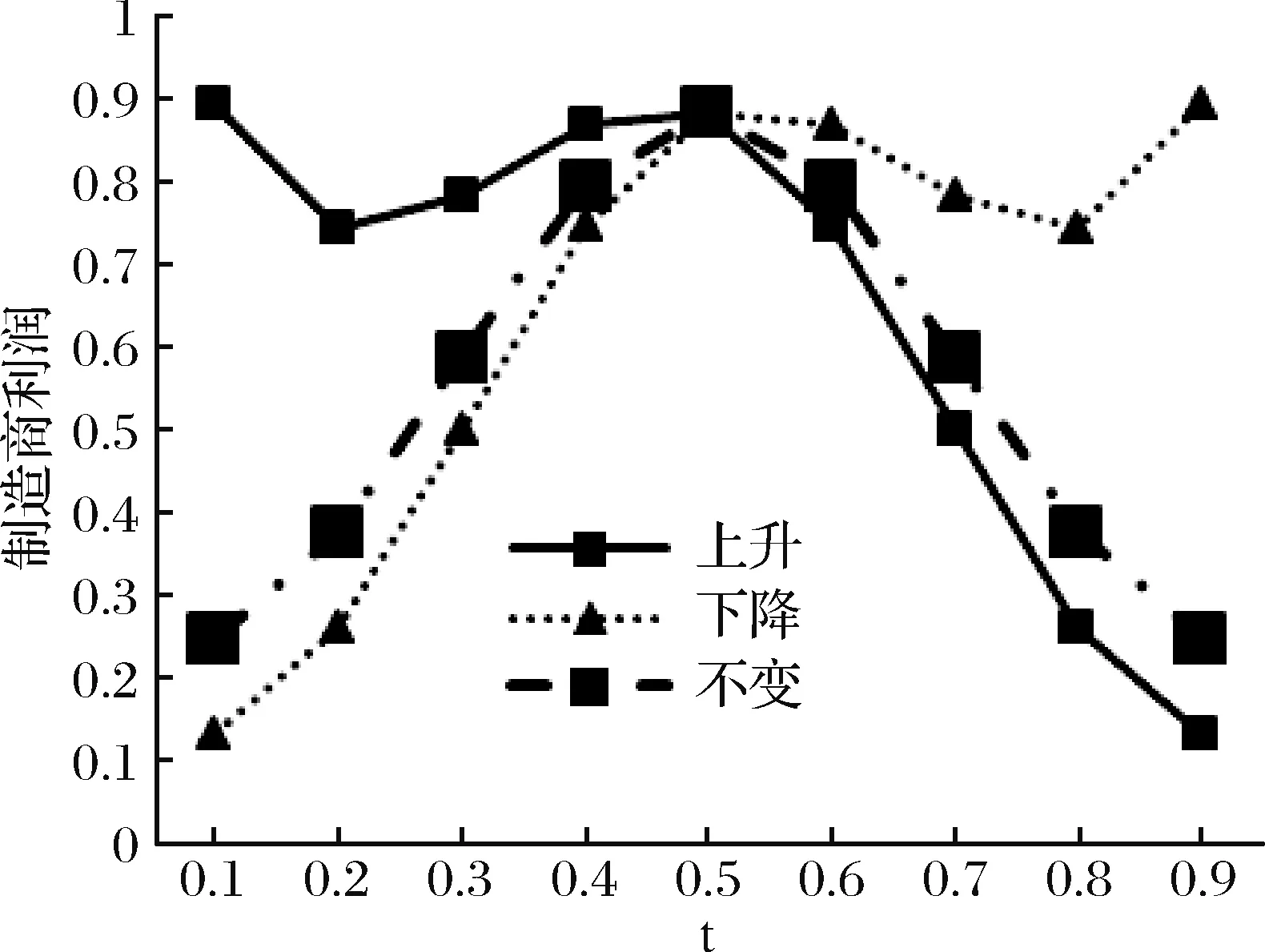
图5 三种情形下制造商的利润的比较分析图

从图5来看，从长期来看，制造商的利润与零售商与制造商间的订购量的变化是一致的。 (1)当零售商的后悔规避程度保持不变时，由于零售商与制造商之间的订购量会随着需求变化，所以制造商的利润先增加后减少；(2)当零售商的后悔规避程度随时间逐渐加强时，由于均衡订购量的减少，所以制造商利润也会呈下降趋势；(3)当零售商的后悔规避程度随时间逐渐减少时，由于订购量的逐渐增加使得制造商的利润也呈上升趋势。

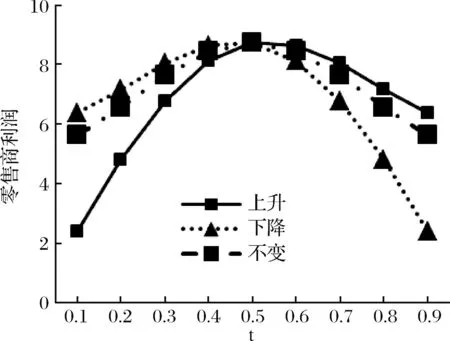
图6 三种情形下零售商的利润的比较分析图

从图6看出，从长期来看，无论零售商的后悔规避程度保持不变、随时间增大，还是随时间减少，其利润都会随着市场需求的变化而变化，先增后减。

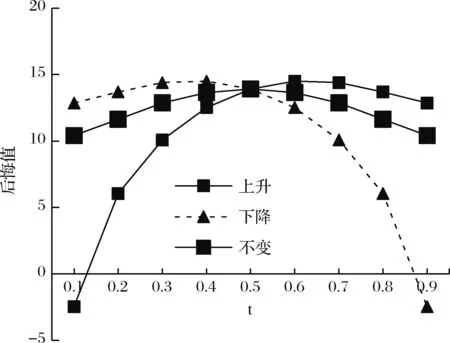
图7 三种情形下零售商后悔值的比较分析图

从图7看出，从长期来看，零售商的后悔规避程度的变化对后悔值的影响较大。(1)当零售商的后悔规避程度保持不变时，其后悔值也基本保持不变；(2)当零售商的后悔规避程度随时间逐渐增大时，零售商的后悔值也会呈上升趋势；(3)当零售商的后悔规避程度随时间的逐渐减少时，对于后悔值来说也会越来越少。

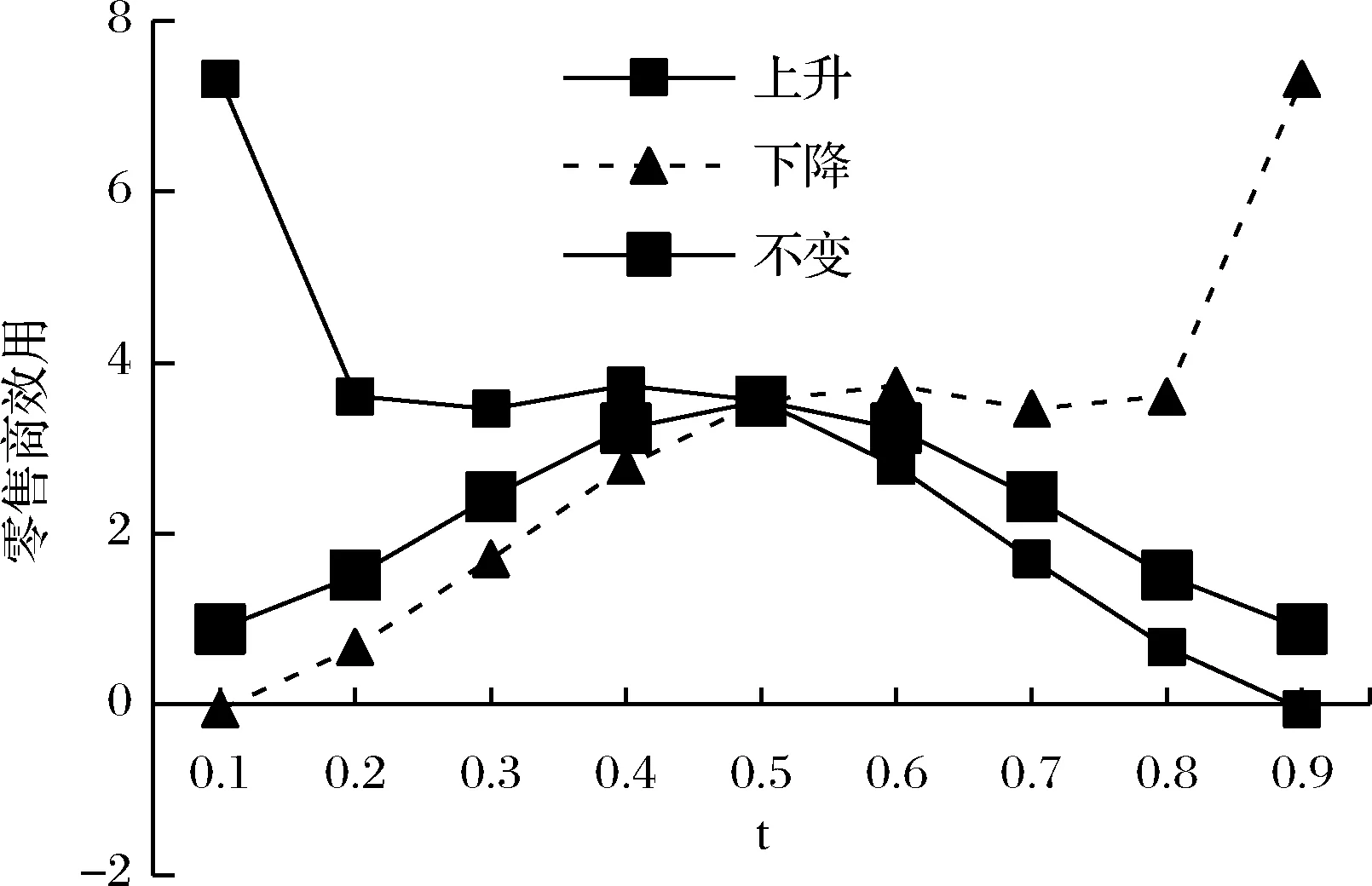
图8 三种情形下零售商的效用的比较分析图

从图8看出，从长期来看，零售商效用的变化同时受到其利润和后悔值的影响。(1)当零售商的后悔规避程度一直保持不变时，其利润随市场需求的变化而变化，先增加后减少，而后悔值基本保持不变，综合来看，其效用也会表现出先增加后减少的趋势；(2)当零售商的后悔规避程度随时间逐渐增大时，利润仍保持先增加后减少的趋势，而其后悔值却呈上升趋势，所以其效用也会呈现出下降的趋势；(3)当零售商的后悔规避程度随时间逐渐减少时，由于受到利润和后悔值的双重影响，所以效用会呈现上升趋势。

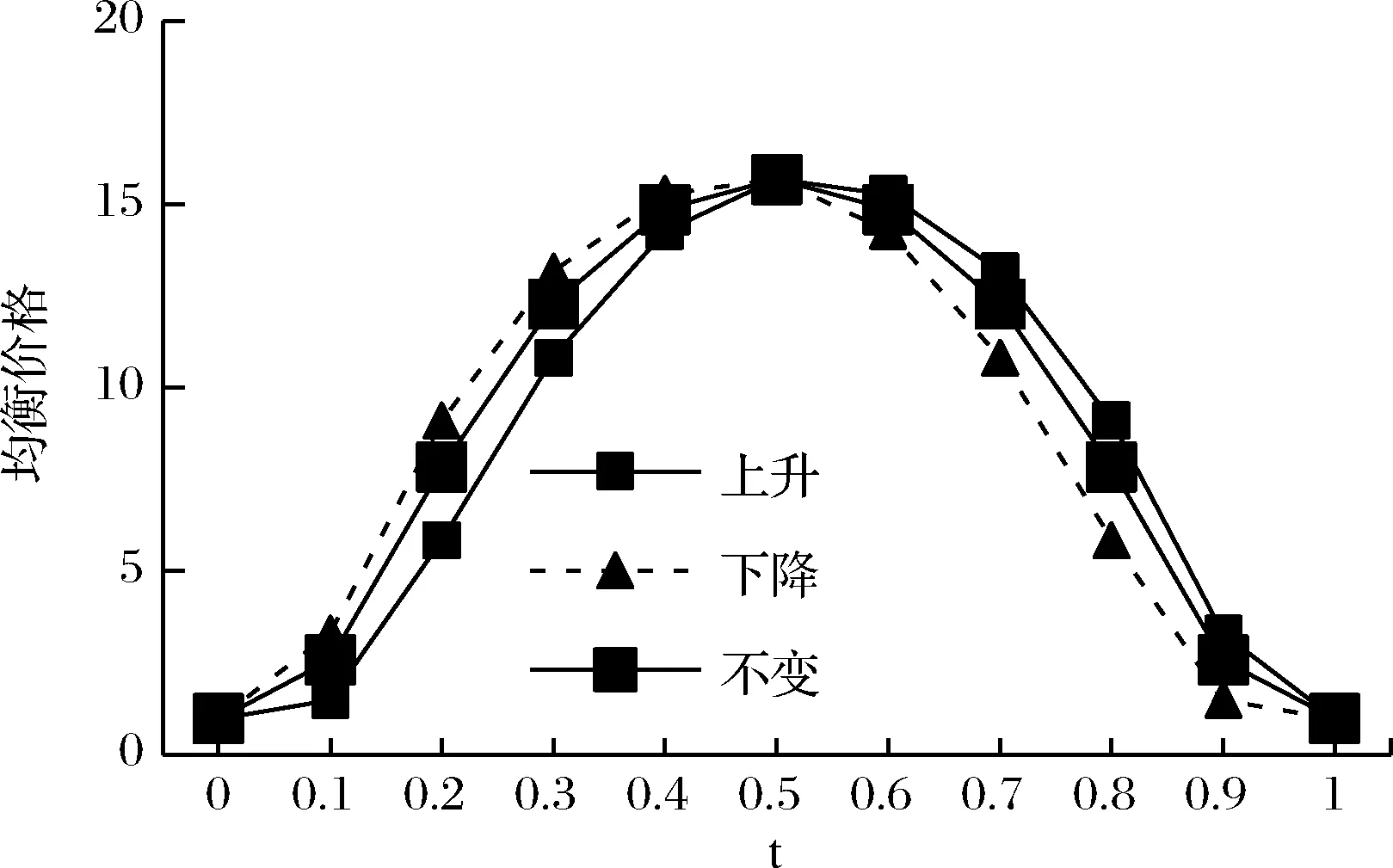
图9 三种情形下市场需求均衡价格的比较分析图

从图9看出，从长期来看，零售商与需求市场的均衡价格的变动与需求市场的变动相似，这说明零售商的后悔规避性对均衡价格的影响力很小，主要是受到了需求市场的影响。所以在三种情形下，均衡价格的变动趋势都是先增加后减少的。

4.2 算例2

在[0,1]时间内，分析零售商后悔规避系数的变化速度对均衡订购量、效用、后悔值的影响。

在算例1的基础上，对情形1(δ(t)=A*t)和情形3(δ(t)=A*(T-t))，调整零售商的后悔规避系数变化的速度，即调整参数A的取值，其中情形2中零售商的后悔规避系数变化速度影响不明显，所以不再讨论。

参数A由10变为20，对情形1和情形3，分别求解变分不等式(18)得到数值结果。得到情形1中的参数A的变化对零售商后悔值、效用和均衡订购量的影响，如图10-12所示；情形3中的A参数A的变化对零售商后悔值、效用和均衡订购量的影响，具体分析如图13-15所示。

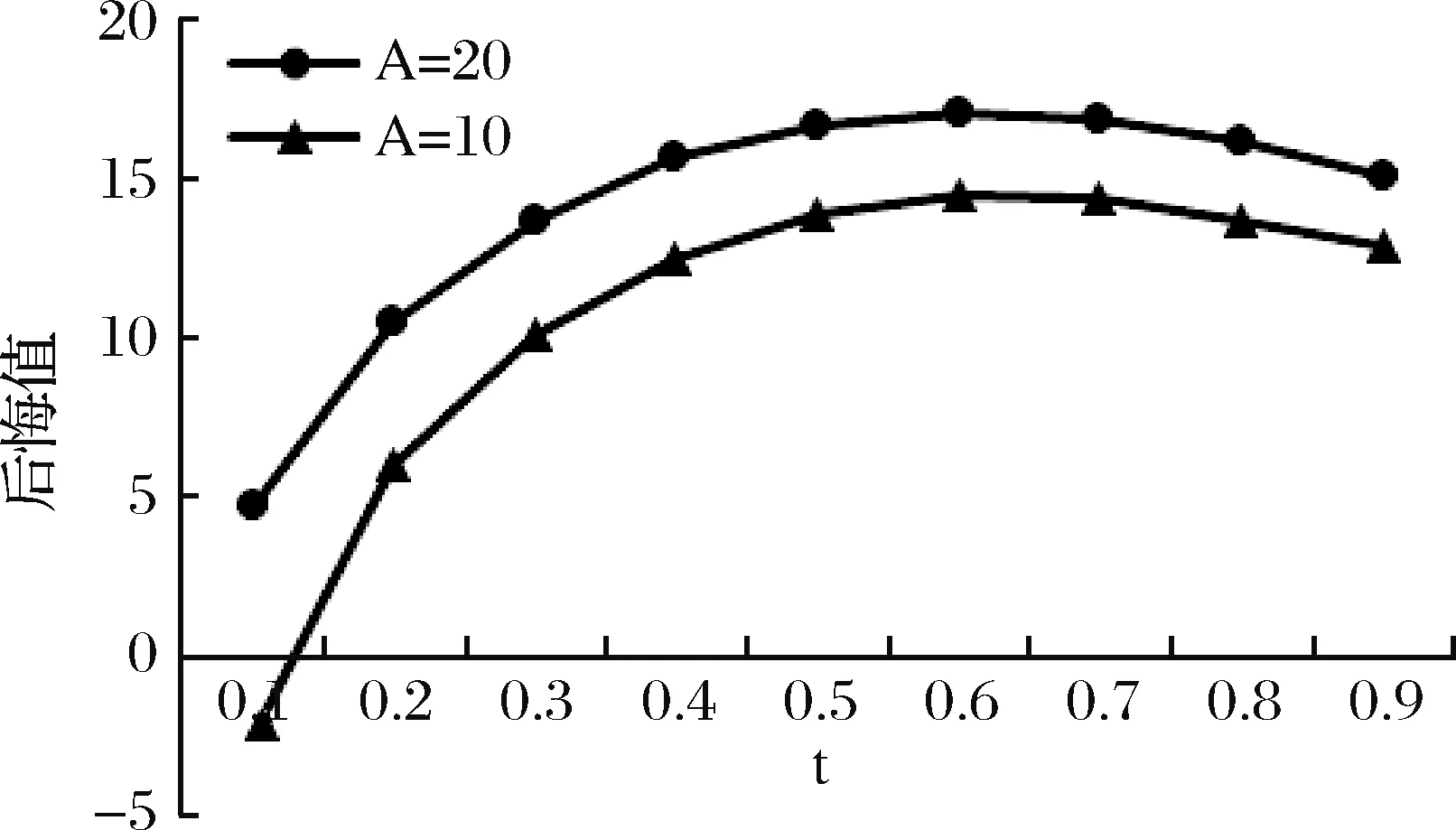
图10 情形1中参数A的变化对零售商后悔值的影响图

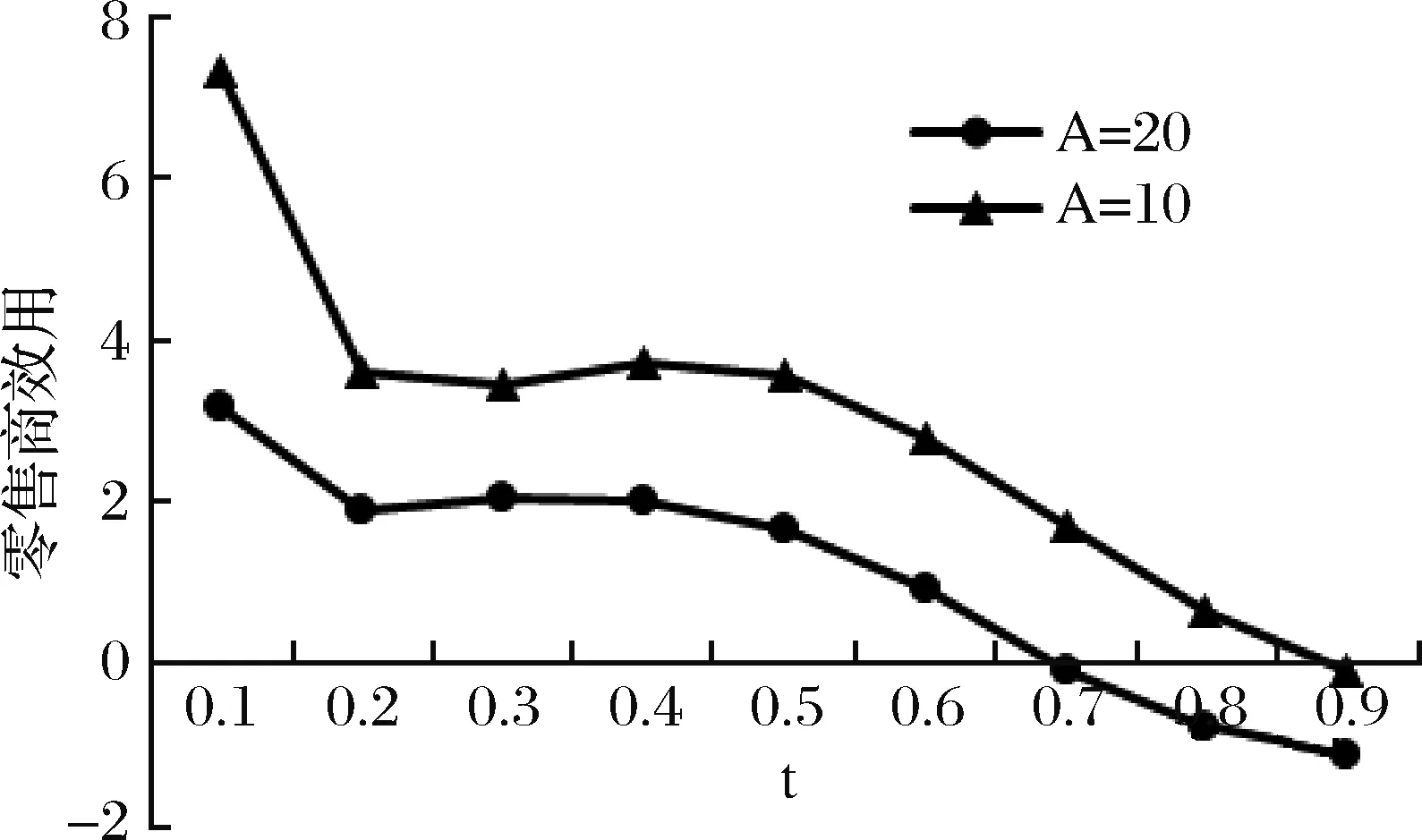
图11 情形1中参数A的变化对零售商效用的影响图

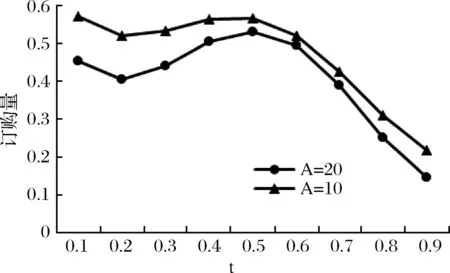
图12 情形1中参数A的变化对订购量的影响图

从图10-12看出，情形1中零售商的后悔规避系数变化的速度由10变为20，即后悔规避的上升表现的更加明显，因此与A=1 0比较其后悔值偏大，影响其订购量、效用均偏小。

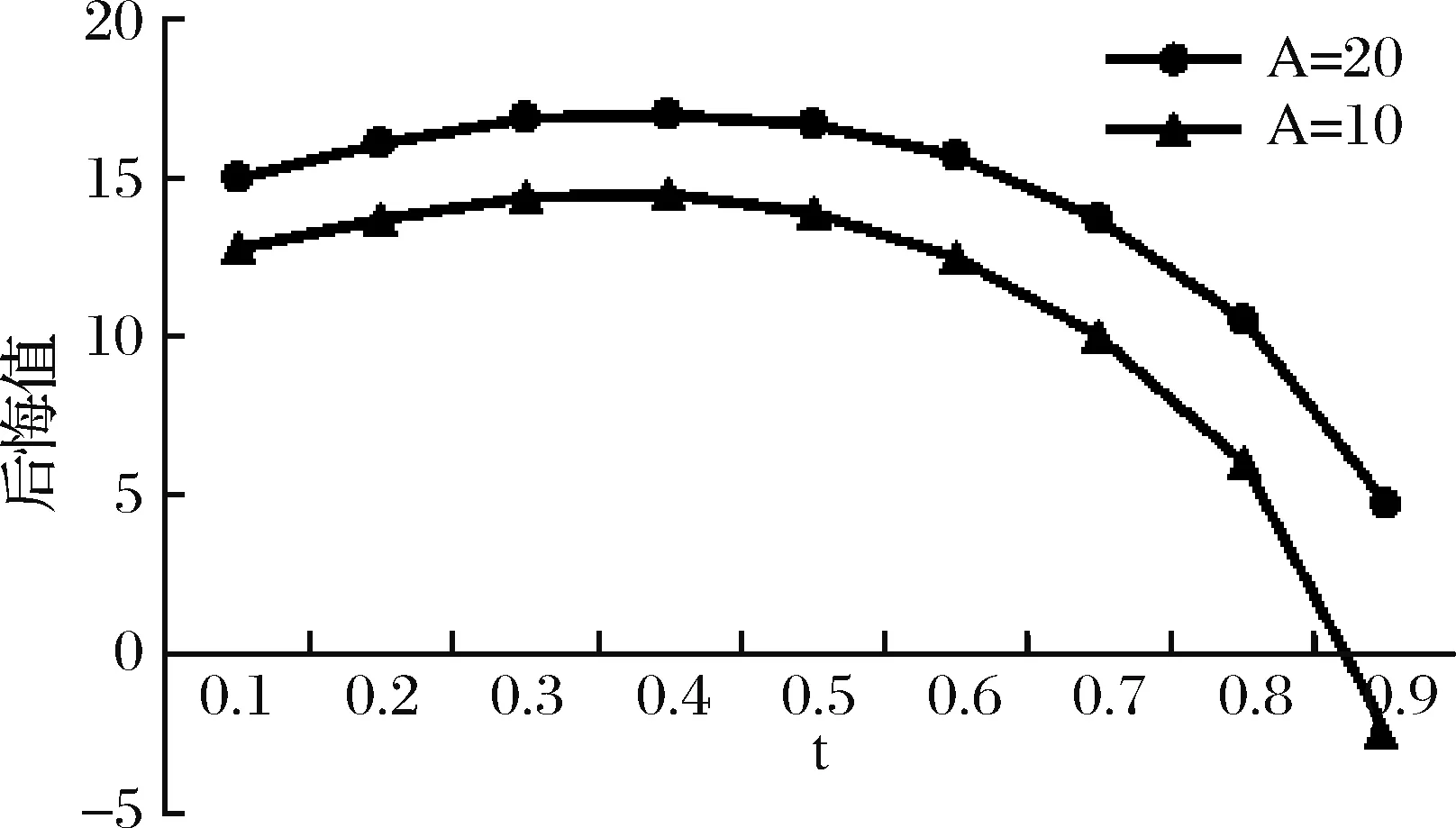
图13 情形3中参数A的变化对零售商后悔值的影响图

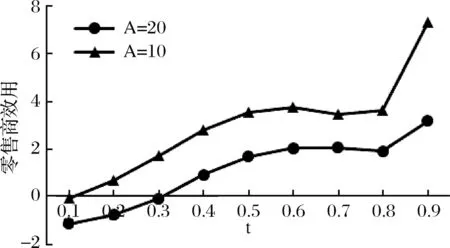
图14 情形3中参数A的变化对零售商效用的影响图

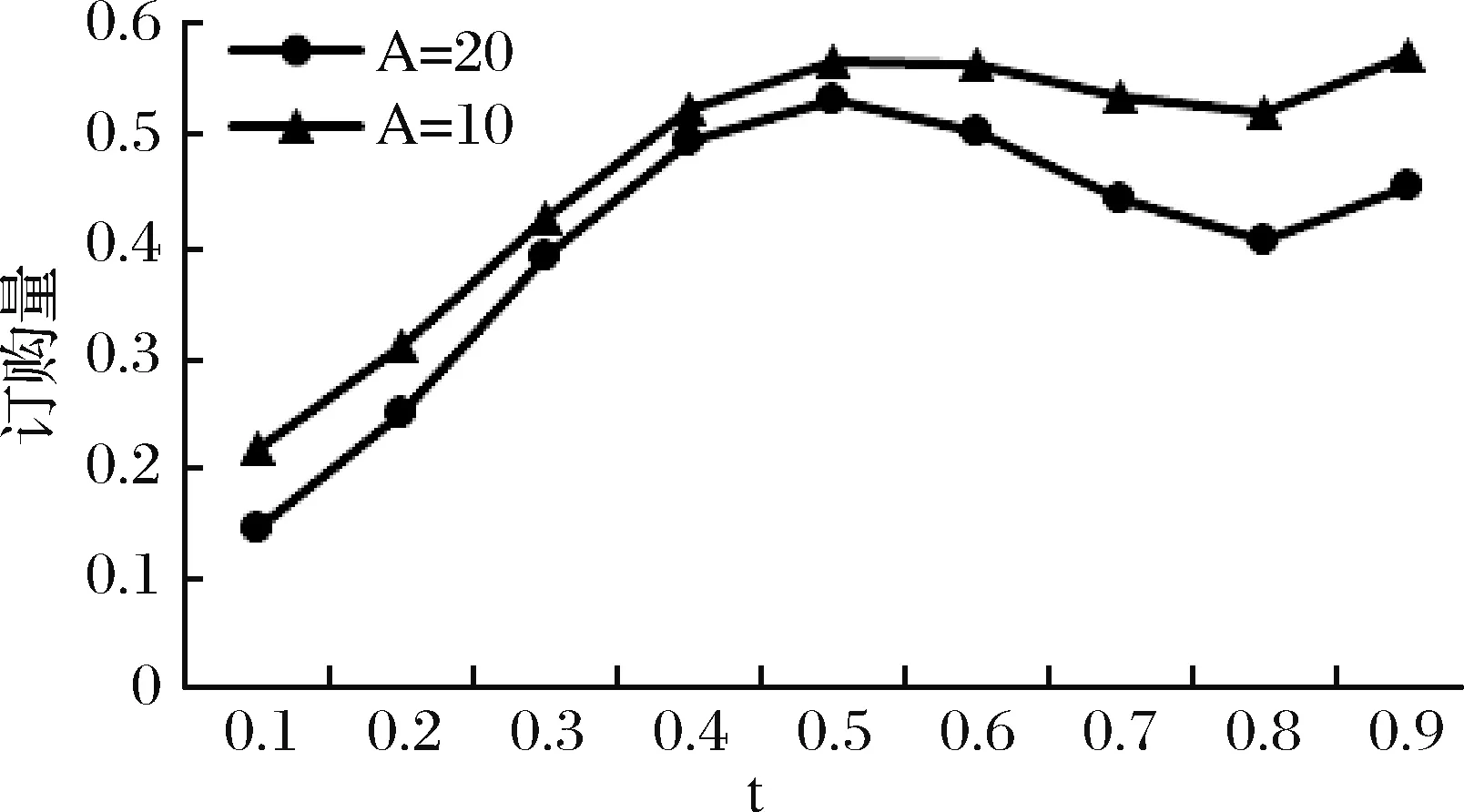
图15 情形3中参数A的变化对订购量的影响图

从图13-15看出，情形3中零售商的后悔规避系数变化的速度由10变为20，即后悔规避的下降速度变得更快，其对零售商后悔值、效用、订购量的影响与情形1相同，即与A=1 0比较，其后悔值偏大，订购量、效用均偏小。

5 结语

本文在时变随机需求的供应链网络动态均衡问题中，分析了零售商长期后悔规避程度的心理变化，对整个供应链网络动态均衡情况的影响。研究结果表明：

(1)当零售商的后悔规避程度在一段时间内保持不变时，均衡订购量、制造商利润，零售商利润、效用都会随着市场需求的变化，先增加后减少。此时，市场需求的变化为主要影响因素。 在此情形下，制造商与零售商都应积极做好市场的调研工作，充分了解和把握市场需求，积极拓展市场，以实现利润和效用的最大化。

(2)当零售商后悔规避程度在一段时间内不断增加时，均衡订购量、制造商的利润会随之减少，而零售商的利润仍保持与市场需求相同的变化，但其效用却会随之减少。在此情形下，制造商在日常生产经营中，应从零售商的多种行为理论和心理认知角度出发，采用积极的措施与零售商进行交易，如可退货策略，二次订购策略，鼓励零售商多订多销，避免长期后悔造成的负效用。

(3)当零售商后悔规避程不断减少时，其均衡订购量和制造商的利润会呈上升趋势，零售商的利润仍保持与市场需求相同的变化，但效用却会增加。在此情形下， 制造商和零售商应积极应对，把握机遇，实现自身利益的同时，实现效用最大化。

通过对零售商长期后悔规避心理变化的研究，为供应链网络中企业的基于长期后悔规避，制定最优决策提供参考。 未来可以考虑零售商多个有限理性行为对供应链网络均衡决策的影响。

参考文献：

[1] Loomes G, Sugden R. Regret theory: An alternative theory of rational choice under uncertainty[J]. Economic Journal, 1982, 92(368): 805-824.

[2]Perakis G, Roels G. Regret in the newsvendor model with partial information[J].Operations Research, 2008, 56(1): 188-203.

[3] Ayvaz-Cavdaroglu N, Kachani S, Maglaras C. Revenue management with minimax regret negotiations[J].Omega,2016,63(8):12-22.

[4] Fujii Y, Okura M, Osaki Y. Regret, rejoicing, and mixed insurance[J]. Economic Modelling, 2016, 58: 126-132.

[5] Chassein A, Goerigk M. Minmax regret combinatorial optimization problems with ellipsoidal uncertainty sets[J]. European Journal of Operational Research, 2017, 258(1): 58-69.

[6] Gilbert H, Spanjaard O. A double oracle approach to minmax regret optimization problems with interval data[J]. European Journal of Operational Research, 2017, 262(3): 929-943.

[7] Skelton A C H, Allwood J M. Questioning dem and: A study of regretted purchases in Great Britain [J]. Ecological Economics, 2017, 131: 499-509.

[8] Wang Jiamin, Xiao Baichun. A minmax regret price control model for managing perishable products with uncertain parameters[J]. European Journal of Operational Research, 2017, 258(2): 652-663.

[9] 饶俪琳, 梁竹苑, 李纾. 行为决策中的后悔[J]. 心理科学, 2008, 31(5): 1185-1188.

[10] 张晓, 樊治平, 陈发动. 基于后悔理论的风险型多属性决策方法[J]. 系统工程理论与实践, 2013, 33(9): 2313-2320.

[11] 袁媛, 刘洋, 樊治平. 考虑后悔规避的突发事件应急响应的风险决策方法[J]. 系统工程理论与实践, 2015, 35 (10) :2630-2636.

[12] 韩菁, 叶顺心, 柴建，等. 基于后悔理论的混合型多属性案例决策方法[J]. 中国管理科学, 2016, 24(12):108-116.

[13] 于超, 樊治平. 考虑决策者后悔规避的风险投资项目选择方法[J]. 中国管理科学, 2016, 24(6): 29-37.

[14] 张华民, 周岩, 徐明姣,等. 基于零售商最小最大后悔值的多准则供应链网络均衡模[J].中国管理科学, 2016, 24(11):7-13.

[15] 高鹏, 杜建国, 聂佳佳, 等. 消费者后悔预期对竞争型再制造供应链权力结构的影响[J]. 中国管理科学, 2017, 25(1): 78-87.

[16] 李梦, 黄海军. 后悔视角下的多用户多准则随机用户均衡模型[J]. 系统工程理论与实践, 2017, 37(5): 1322-1330.

[17] Gilovich T, Medvec V H. The experience of regret: What, when, and why[J]. Psychological Review, 1995, 102(2): 379-395.

[18] Abendroth L J, Kristin D. Now or never: Effects of limited purchase opportunities on patterns of regret over time[J]. Journal of Consumer Research, 2006, 33(3): 342-351.

[19] 张结海. 短期后悔与长期后悔的差异:三种不同的解释[J]. 心理科学进展, 2000, 18(4): 63-225.

[20] Nagurney A, Dong J, Zhang Ding. A supply chain network equilibrium model[J]. Transportation Research Part E, 2002, 38(5): 281-303.

[21] Dong J, Zhang Ding, Nagurney A. A supply chain network equilibrium model with random demands[J]. European Journal of Operational Research, 2004, 156(1): 194-212.

[22] Daniele P. Evolutionary variational inequalities and applications to complex dynamic multi-level models[J]. Transportation Research Part E,2010, 6(6):855-880.

[23] Nagurney A, Yu Min, Floden J, et al. Supply chain network competition in time-sensitive markets[J]. Transportation Research Part E, 2014, 70: 112-127.

[24] Feng Zhifang, Wang Zhiping, Chen Yan. The equilibrium of closed-loop supply chain supernetwork with time-dependent parameters[J]. Transportation Research Part E, 2014, 64(1): 1-11.

[25] 孙嘉轶, 滕春贤, 陈兆波. 基于微分变分不等式的再制造闭环供应链网络动态模型[J]. 系统工程理论与实践, 2015, 35(5): 1155-1164.

[26] 张桂涛 ,胡劲松, 孙浩,等，考虑损失规避零售商的多期多产品供应链网络均衡[J]. 中国管理科学, 2015, 23(6):73-82.

[27] Chorus C G. Regret theory-based route choices and traffic equilibria[J]. Transportmetrica, 2012, 8(4): 291-305.

[28] Korpelevich G M. The extragradient method for finding saddle pointsand other problems[J]. Matecon, 1976, 12: 747-756.