基于第一性原理的新型非线性光学晶体探索∗
2018-06-19梁飞林哲帅吴以成
梁飞 林哲帅 吴以成
1)(中国科学院理化技术研究所,功能晶体与激光技术重点实验室,北京 100190)
2)(中国科学院大学,北京 100049)
3)(天津理工大学,功能晶体研究院,天津 300384)
(2018年1月26日收到;2018年4月12日收到修改稿)
1 引 言
通过激光频率转换技术,非线性光学晶体可将常见波段的激光(如近红外1064 nm激光)转换至新的波段,实现紫外、中远红外乃至太赫兹波段激光的输出.这种光电功能晶体是一类光子耦合的“催化材料”,具有转换效率高、光束质量好、可调谐、小型化、易于操控等突出优点,已被广泛应用于全固态激光器中,在光谱学、通讯和光计算、生物成像、精密制造等科技及工业前沿领域具有重要和广泛的应用[1,2].可以说,非线性光学晶体是全固态激光频率转换系统的核心元件,也是迫切需要不断优化和发展的关键要素.

林哲帅,中国科学院理化技术研究所研究员.2002年获中国科学院福建物质结构研究所博士学位.主要从事新型光电信息功能材料的计算机模拟和分子工程学设计.主持或参与多项国家自然科学基金重点、面上项目及国家973、863等项目.在Adv.Mater.,JACS,Angew Chem.,Nat.Comm.等学术期刊发表SCI论文200余篇.
根据应用波段的不同,非线性光学晶体可以分为紫外区、可见和近红外区及中远红外(含太赫兹波段)区非线性光学晶体.在紫外和可见光区,中国学者取得了举世瞩目的成果,其中BBO(β-BaB2O4)和LBO(LiB3O5)晶体在Nd:YAG激光二倍频、三倍频、四倍频研究中被广泛应用,被誉为“中国牌”晶体[3,4].在深紫外区(波长小于200 nm),KBBF(KBe2BO3F2)晶体是惟一可实用化产生深紫外谐波的非线性光学晶体.2015年,利用KBBF晶体获得最高输出功率达到200 mW的177.3 nm激光,为KBBF进一步实现产业化奠定了基础[5].在可见近红外区,KTP(KTiOPO4)晶体具有频率转换效率高、倍频系数大、损伤阈值高、透过范围宽和化学稳定好等优点,被誉为激光频率转换领域的“全能冠军”,是可见近红外区频率转换晶体的首选[6].
20世纪80年代以来,以南京大学闵乃本院士为代表的研究团队[7]提出了“介电体超晶格”的概念,将准晶结构引入介电体超晶格,建立了“多重准位相匹配理论”,发明了室温图案极化新技术,研制出能同时产生多种颜色激光的准周期超晶格和全固态红、绿、蓝三基色和白光激光器样机.另外,闵院士团队[8,9]还研究了在光波、微波、声频三个波段内微结构对物理性质的影响,在光电子学、声电子学、材料科学的交叉领域中催生了称为“畴工程学”的新学科.该系列成果于2006年获国家自然科学一等奖.
在中远红外区,黄铜矿型的AgGaS2,AgGaSe2和ZnGeP2晶体已经实现了商业化应用.2017年,我国科学家利用自主生长的ZnGeP2晶体,经过电子辐照和退火处理后,实现了目前国际上最高效率的光学参量振荡(OPO)输出,峰值功率密度高达24 MW/cm2,光光转换效率达到75.7%[10].近年来,我国科学家陆续生长了LiInSe2[11],BaGa4S7[12],BaGa4Se7[13]等新型的红外非线性光学晶体,并实现了光学参量放大(OPA)和OPO激光输出[14,15].这些成果充分说明了新型硫族化合物在中红外非线性频率转换领域的应用潜力.
在太赫兹(THz)波段,常见的无机太赫兹晶体有LiNbO3,GaSe,ZnGeP2等,其THz调谐输出能量较高,但是调谐范围大多集中在5 THz以下.常见的有机太赫兹非线性光学晶体有4-(4-二甲氨基苯乙烯基)甲基吡啶对甲苯磺酸盐(DAST),4-(4-二甲氨基苯乙烯基)甲基吡啶2,4,6-三甲基苯磺酸盐(DSTMS)和2-(3-(4-羟基苯乙烯基)-5,5-二甲基环己-2-烯亚基)丙二腈(OH1).这些晶体非线性光学系数更大,THz调谐范围也更宽.吴以成院士课题组[16]通过改善生长条件,生长出了大尺寸、高质量的DAST,DSTMS,OH1单晶.2015年,他们与天津大学姚建铨课题组合作,在DSTMS和OH1晶体中实现了0.9—19.7 THz和0.02—20 THz波段的调谐输出,是目前已报道的利用DSTMS和OH1晶体差频方法产生单频可调谐THz波的国际最高水平[17,18].
尽管已取得辉煌的成就,然而已发现的非线性光学晶体并不能满足当今激光技术迅猛发展的需求,尤其是应用于深紫外、中远红外以及太赫兹波段的非线性光学晶体还亟待研发.目前新型非线性光学晶体研究的趋势是:1)探索新的结构基元,发展新的功能材料基因,并力图实现不同功能基因的组合;2)合理的元素取代,替换晶体生长过程中会使用到的有毒原料;3)在清晰的结构功能关系的基础上,改善和优化非线性光学材料的性能.探索新型的非线性光学晶体一直是功能材料学界的一个前沿领域和研究热点[19].
目前来看,传统的炒菜式的实验方法已经不足以满足大规模高通量的非线性光学材料的探索,必须和第一性原理方法相结合.这主要体现在两个方面:1)实验探索进度相对缓慢,很难快速确认一种新材料是否具备深入研究的价值,而第一性原理计算是快速而高效的,只要有了晶体结构,就可以在短时间计算大量新材料的非线性光学性能;通过特定限制条件的选择,可以迅速地将有研究价值的材料筛选出来,这一点已经在我们前期的研究工作中有了明显的体现,例如我们已经成功地从接近100种金属硫磷化合物中筛选出了AgZnPS4这一具有研究价值的新型红外非线性光学晶体[20];2)实验上得到了好的结果以后,仅靠实验本身,无法分析其优异的非线性光学性能的来源,第一性原理方法可以提供原子和电子层次上的微观分析工具,对材料的非线性光学效应的来源进行系统而深入地剖析,加深对某一大类新材料的结构与性能之间的认识,从而为进一步描绘新晶体设计的蓝图打下基础.目前,常见的CASTEP,VASP,Abinit等计算程序包均可用于非线性光学系数的计算,并取得了和实验值比较符合的结果[21−23].在下面的章节中,我们将重点阐述第一性原理方法在新型非线性光学晶体探索中的应用;在紫外、中红外非线性光学晶体探索中进行分子设计;讨论在深入研究构效关系的基础上,如何建立以分子工程学为基础的专家系统;展望第一性原理方法用于非线性光学晶体探索的发展方向.
2 利用第一性原理方法获得光学参数和构效关系
决定非线性光学晶体性能的本征关键光学参数主要包括带隙、倍频系数和双折射.材料计算模拟方法不仅能够较准确地预测非线性光学晶体的关键光学参数,还可以定量和直观地分析其与晶体结构特征之间的内在关系.我们采用的计算方法是基于密度泛函理论(DFT)的随机相位近似[24]方法,对含时密度泛函[25],Bethe-Salpeter方程[26]等方法并未深入研究.对于倍频系数的计算,采用由Rashkeev等[23]推导并经本课题组与台湾淡江大学李明宪教授课题组合作完善的计算公式[27]((1)—(4)式),通过共同开发的CASTEP计算子程序获得.对于一个特定的非线性光学系数分量,它的贡献主要来自于3部分:1)虚电子(virtual electron,VE)跃迁的贡献((2)式);2)虚空穴(virtual hole,VH)跃迁的贡献((3)式);3)双带(two bands)跃迁的贡献((4)式).通常而言,3)的贡献是非常小的,基本可以忽略不计.虚电子和虚空穴的贡献则与晶体材料电子的价带和导带的态密度密切相关.
我们所推导得到的倍频计算公式如下:

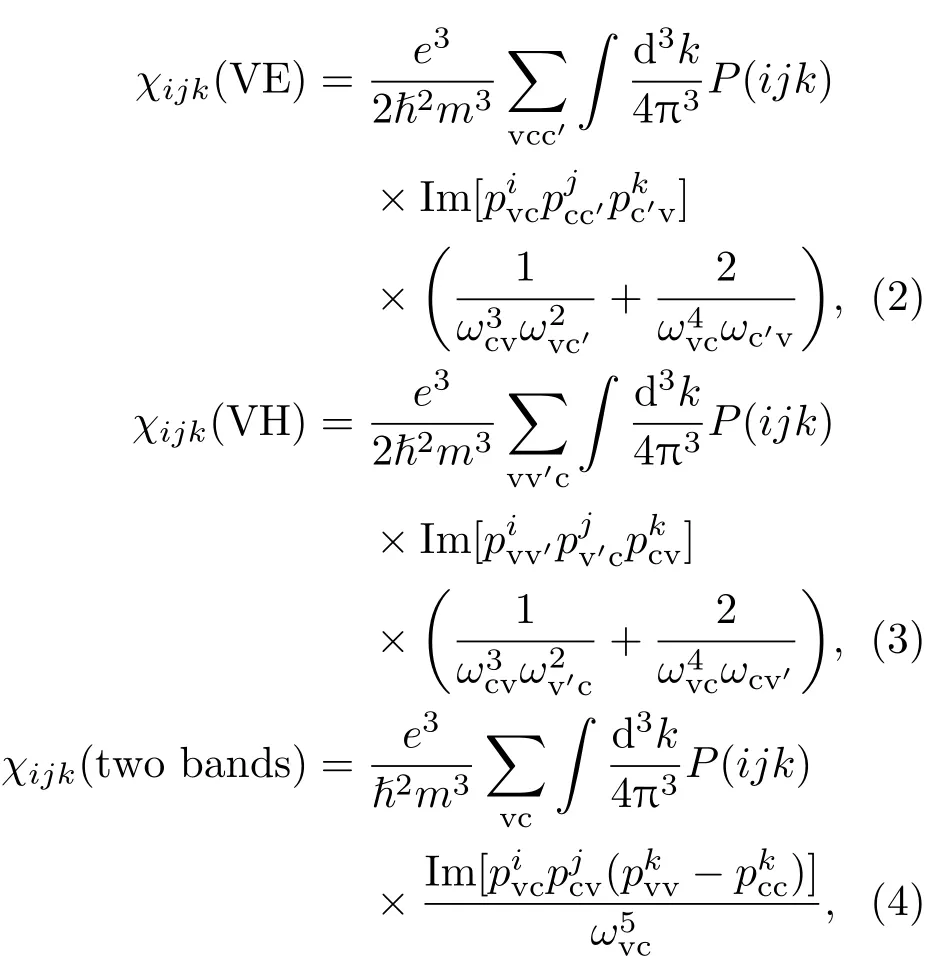
式中e是电子电荷,m是电子的静态质量,}是约化的普朗克常数,P(ij k)表示全交换,下标v和c分别代表价带和导带,ωcv为导带和价带之间的频率之差,pcv代表相应的动量跃迁矩阵元.
二阶非线性光学转换过程是一个虚激发参量过程,光子并没有真正地从价带跃迁到导带上,因此只要准确计算基态的波函数,就可以得到准确的二阶非线性光学系数.但是由于二阶非线性光学系数计算的公式依赖于带隙值Eg,而使用PBE(Perdew-Burke-Ernzerh)或者局域密度近似(LDA)泛函的DFT计算一般会低估带隙Eg,因此需要使用剪刀算符移动导带的位置,以获得与实验相符的短波截止边.为了实现真正无经验参数的第一性原理计算,我们采用了杂化泛函计算:对于紫外、深紫外化合物使用PBE0泛函,对于中红外化合物使用sX-LDA或者HSE06泛函.大量的计算测试表明,这样的选取可获得较为准确的带隙值[28,29].由于杂化泛函计算要求的资源较大,我们采用直观判定影响材料带隙的电子云分布的方法,提出了“非键轨道分析”和“MBVS带隙预测方法”[30,31],可直接从材料的原子构型出发,准确地预测光学材料的带隙.此外,在我们前期的参数测试中,测量光学性质选取的导带空带数也很重要,一般而言应该至少是计算时考虑的价带总数的3倍,才能得到比较准确的计算结果.

表1 不同体系的非线性光学材料计算和实验性能参数Table 1.Calculated and experimental parameters of various nonlinear optical materials.
一种新发展的计算方法是否适用,第一要素就是检验其与已有实验数据的符合度.只有能够较好地重复出实验结果的方法,才是可靠的、值得信赖的方法.为此,我们挑选了一些典型的非线性光学晶体材料,包括硼酸盐、磷酸盐、碳酸盐、硫化物、硒化物、磷化物等,其实验值与理论计算值列于表1中[32,33].从表1可以看出,我们计算的结果与实验值有极高的符合度.对宽带隙的氧化物,各项性能指标的误差一般小于20%;对窄带隙的硫族、磷族化合物,各项性能指标的误差一般小于30%.考虑到第一性原理方法不引入任何经验参数,这已经是一个相当好的结果,也为以后的性能预测与构效关系分析打下了坚实的基础.
2.1 实空间原子切割方法
利用前面公式得到的倍频系数是晶体整体表现出的物理量,并不能从中得到晶体结构中某一个特定基团对光学性质的贡献大小.为此,本课题组与李明宪教授课题组合作开发了实空间原子切割方法,可定量分析各个结构基元对光学性质的贡献[27].其基本思想是,将某一种特定基团包含的原子挑选出来,按照合理的半径进行球形切割,对切割半径之内的电子波函数进行保留,对切割半径之外的波函数做归零处理(“切割去除”),然后重新计算光学跃迁矩阵元,即可求出该未被切割去除部分对光学性质的贡献大小.
如表2所列,我们对BBO和LBO两种非线性光学晶体进行了原子切割[27,34].可以看出,对几个主要的非线性光学系数分量,碱金属和碱土金属对光学性质的贡献非常小,而硼氧基团则起到核心作用.这与陈创天院士等[35]提出的阴离子基团理论得到的结论一致.利用实空间原子切割技术,不仅可以得到阴离子基团对光学性质的贡献,还可得到阳离子对光学性质的贡献.这相比阴离子基团理论更进一步.实空间原子切割方法在分析阴离子基团和孤立A位阳离子相互作用较弱的晶体上特别有优势(比如BBO晶体孤立的(B3O6)基团和Ba2+离子,KBBF晶体中二维的(Be2BO3F2)基团和K+离子),但对于某些阳离子和阴离子基团相互作用比较强的系统,这一方法的使用要格外小心.
1)首先要对晶体结构进行合理划分,不能一味地将碱金属、碱土金属、稀土金属视为孤立阳离子.以非线性光学晶体La2CaB10O19(LCB)为例[36],长期以来,La3+和Ca2+都被视为孤立阳离子,在传统阴离子基团的框架下,其非线性光学效应的来源被视为是B5O12基团.第一性原理计算其非线性光学系数d21为0.58 pm/V,与实验值完美匹配.但是原子切割的结果显示,B5O12,Ca2+,La3+的贡献分别为0.46,0.01,0.06 pm/V.这样得到的切割结果偏小,说明有一部分贡献被忽略了.后来经过仔细检查原子与原子之间的成键强度,我们认为La3+不应该被视为孤立的金属阳离子,而应该和周围的10个氧原子共同视为LaO10阴离子基团,这样LaO10的贡献为0.19 pm/V,远大于孤立的La3+阳离子.与之相比,Ca2+与周围的O原子相互作用弱,仍应该视为孤立的阳离子.这样就对LCB晶体中的非线性光学效应来源有了更为明确的认识,为后续含稀土的非线性光学材料设计提供了更多参考.

表2 BBO和LBO晶体中各个离子基团对于光学性质的贡献Table 2.Contribution of respective ionic groups to optical properties in BBO and LBO.
2)对含有Pb2+,Bi3+,Sn2+等金属阳离子的体系,也要特别小心.一般来说,这些阳离子都有孤对电子效应,可以产生较强的非线性光学响应,如BiB3O6,PbB4O7等.在对这些阳离子做切割时,传统的球形切割不太适用,需要继续发展沿着电子密度奇点位置的切割方式,这一方法正在发展中.
2.2 倍频密度分析图
实空间原子切割方法对分析晶体结构中的构效关系十分有效,但这种方法很难直观地判断晶体中特定原子在光学性质中所扮演的角色.为此,我们和李明宪教授合作,进一步发展了倍频(SHG)密度分析方法[37].该工具可以将晶体中某一类基团以及基团中的原子对倍频效应的贡献直观地表示出来,在构效关系的可视化进程中迈出了一大步. 在此,我们以β-Sr3(C3N3O3)2(β-SCY)晶体为例[38],介绍该工具的功能.
如图1所示,SHG的贡献来源可以分为4类:1)虚电子占据态;2)虚电子未占据态;3)虚空穴占据态;4)虚空穴未占据态.其中未占据态对应着禁带中虚激发能级,一般其贡献远远小于电子占据态;虚电子的占据态对应着价带顶的电子分布,虚空穴的占据态对应着导带底的电子分布.在SCY晶体中,虚电子的占据态主要由平面(C3N3O3)基团中的O和N贡献,而虚空穴的占据态则主要由平面(C3N3O3)基团中的O和C贡献.这些情况一方面可以在电子密度图上体现出来,另一方面也可以在SHG密度图上直接地展现,而且可视化程度更高.此外,利用这一工具,可以对三维的电子密度进行切割,观察每一个切面上的特征,做到对SHG来源逐点逐面分析.

图1 β-SCY晶体d11系数的倍频密度图 (a)虚电子占据态;(b)虚电子未占据态;(c)虚空穴占据态;(d)虚空穴未占据态;(e)SCY晶体的总电子态密度和分波电子态密度(灰色、蓝色和红色小球分别表示碳、氮、氧原子,红色虚线代表费米能级,倍频电子密度大小由颜色深浅表示,蓝色代表0,红色代表0.1 e/Å3[38])Fig.1.SHG weighted electron densities ofβ-SCY crystal:(a)Occupied and(b)unoccupied VE process;(c)occupied and(d)unoccupied VH process along(C3N3 O3)3− cross section;(e)total/partial electron density of states ofβ-SCY;C,N,and O atoms are represented by gray,blue,and red balls,respectively,the red dotted line represents Fermi level,SHG electron density is represented from blue 0 to red(0.1 e/Å3)[38].
2.3 柔度因子模型
柔度因子是本课题组于2014年提出的一个对SHG来源的新的描述符,用来衡量特定基团在外场扰动下对非线性光学效应的贡献大小[39].柔度因子越大,意味着基团越“软”,有更大的感生偶极矩,继而对非线性光学响应的贡献也更大.它的计算公式为

其中Ca和Cb代表价电子数;Ra代表平均键长;Ro代表标准键长;B是经验常数,通常取0.37Å.显然,分子表示价键电荷数而分母表示原子之间及电子之间的库仑相互作用力.可以看出,柔度因子的值依赖于配位环境和键长,因此它特别适用于分析具有相似晶体结构特征的材料.在此我们以硅酸镓镧(LGS)体系为例,分析寻找La3SnGa5O14(LGSn)这一优秀的非线性光学晶体的过程,该工作与山东大学的张怀金、于浩海课题组合作完成[40,41].
硅酸镓镧体系属于P321空间群,其晶体结构中的金属位置可以分为A,B,C,D 4个位点(图2(a)).首先以LGS为例,采用实空间原子切割方法,分析[A O8],[B O6],[C O4],[D O4]4种功能基团对非线性光学效应的影响.我们证实[LaO8]基团的贡献最大,而且一旦La被替换成碱土金属,其非线性光学效应会迅速下降.因此,为了保持较大的非线性光学效应,La元素不能被替换掉.而[C O4]和[D O4]位置由于对称性的限制,对非线性光学效应的贡献不大.在LGS中,[GaO6]八面体位置的贡献不大,当Ga被部分替换成Ta,Nb以后,LGN和LGT的非线性光学效应相对于LGS均有增强,这就启示我们B位是一个关键的非线性光学效应调控位点.为此,把原子半径更大、原子质量更重的Sn元素引入该结构体系.计算结果显示,LGSn的粉末倍频效应约为LGN的1.6倍,是目前已知的硅酸镓镧体系中效应最强的(图2(b)).我们计算了4种化合物[B O6]基团的柔度因子,发现[SnO6]基团的柔度因子最高(图2(c)),这说明LGSn中增强的非线性光学响应可以归因于[SnO6]基团更强的柔性.于浩海课题组实验合成了纯相LGSn粉末样品,倍频测试表明LGSn的粉末倍频效应约为LGN的2倍,与我们理论计算的结果相符合(图2(d)).在LGSn的发现过程中,理论和实验结合,相互印证,是新型非线性光学材料开发的一个典型例证.
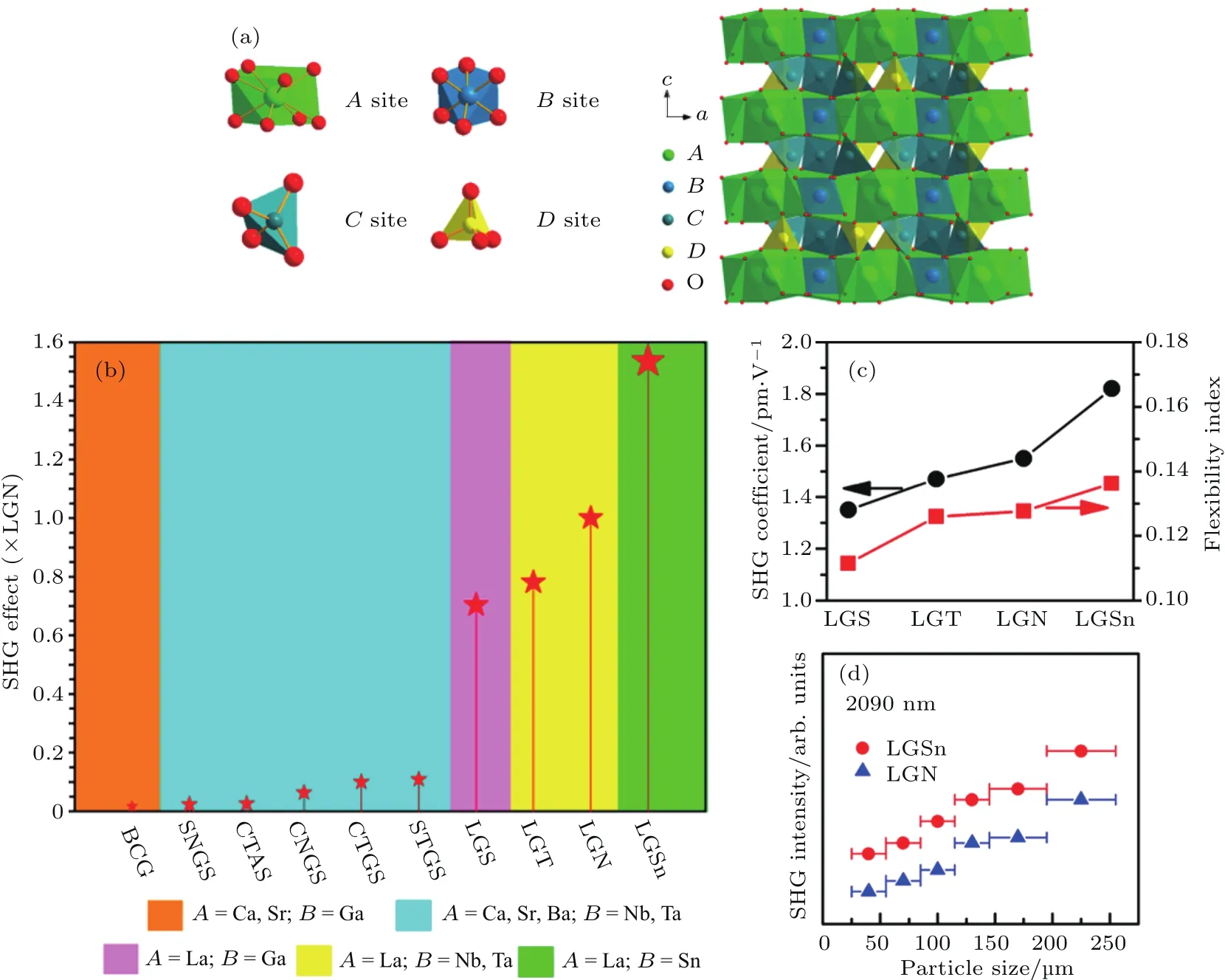
图2 (a)硅酸镓镧系列(A 3BC3D 2O 14)晶体结构示意图(A,B,C,D分别代表八配位、六配位和四配位晶格位点);(b)硅酸镓镧体系中的非线性光学效应与组分的关系;(c)LGS,LGT,LGN和LGSn中非线性光学系数与B位[MO 6]基团的感应柔度之间的关系;(d)波长λ=2090 nm下,LGSn与LGN的粉末倍频效应对比[41]Fig.2.(a)Schematic of crystal structure of langasites:three-dimensional framework,viewed along b axis;the local distorted polyhedron of diff erent cation sites,including decahedral A site,octahedral B site,tetrahedral C site,and tetrahedral D site;(b)the structure-composition-property maps of langasite family structures with diff erent elemental composition on A and B sites;(c)the relationship between SHG coeffi cients and fl exibility index of(MO 6)groups in LGS,LGT,LGN,and LGSn;(d)powder SHG response of LGSn at 2090 nm,LGN is taking as a reference[41].
除了非线性光学系数以外,第一性原理计算还可以得到晶体的带隙、折射率、声子振动性质、杨氏模量等.通过带隙值和声子振动频率,可以估计晶体的紫外和红外透过截止边,从而获得材料的透过区间;通过折射率色散曲线,可以得到材料的相位匹配区间,判断其实用的工作波段;通过计算声子谱,可以定性地给出材料的稳定性,对预测新材料是否存在有关键作用.杨氏模量和体模量的大小可以初步判断材料的硬度和机械加工性能.
总而言之,第一性原理计算方法能够在不借助任何实验参数的情况下得到材料的诸多性质,可以大大加速新材料的研发过程.下面我们从应用于不同光谱区域(深紫外、中红外和太赫兹)的非线性光学晶体以及具有新颖微观结构基元的非线性光学晶体两方面,详细介绍第一性原理方法在新型非线性光学晶体材料研发中的应用.
3 深紫外、中红外和太赫兹新型非线性光学晶体
3.1 深紫外非线性光学晶体探索
深紫外激光在激光光谱学、凝聚态物理、化学反应动力学方面有重大的应用价值.结合已有的成熟的半导体激光技术,发展全固态深紫外光源是国际科学界共同关注的前沿科学问题.目前我国在这一领域保持领先地位,陈创天院士发明的KBBF晶体是目前国际上惟一在Nd:YAG激光器1.064µm六倍频方面得到实际应用的晶体,这一晶体的发现、生长及其应用在国际上产生了重大影响.2006年以来,中国科学院物理研究所和中国科学院理化技术研究所合作,成功地研制了包括真空紫外激光角分辨光电子能谱仪在内的基于深紫外全固态激光源的一系列谱仪[42],这些仪器都是国际首创,指标国际领先.由于KBBF晶体的重要性,《Nature》杂志于2009年专门刊发了一篇文章,以《中国的晶体秘藏(China’s crystal cache)》为题,介绍了KBBF晶体的发展[43].但是,目前KBBF晶体在厚度上存在生长瓶颈,严重阻碍了它的大规模应用.对于KBBF晶体,我们首先要从理论上回答为什么它具有如此优异的深紫外非线性光学性能,然后针对它存在的两个问题,即层状生长习性和原料BeO有剧毒,提出相应的解决方案.
3.1.1 材料的深紫外透过性能
深紫外非线性光学晶体生成的首要条件是在深紫外波段有高的透过率,这就要求晶体的带隙要大于6.25 eV(200 nm),最好位于7.5—8.0 eV.鉴于目前深紫外非线性光学晶体的研究主要集中于强共价性的硼酸盐、磷酸盐体系,我们主要关注该体系化合物的能带特征.
深紫外区非线性光学材料中的功能基团可以分为两大类:一类是含有平面共轭π键的BO3,CO3,B3O6等基团,其电子组态是sp2杂化;另一类是四面体配位的BO4,PO4基团,其电子组态为sp3杂化.一般来说,sp3杂化基团由于没有π轨道,其带隙明显大于sp2杂化基团,比如典型的BPO4和SrB4O7晶体,其带隙达到了10 eV以上,深紫外透过截止边接近130 nm[44,45].在某些磷酸盐体系(Ba3P3O10Cl)中[46],通过对卤素原子的合理剪裁,带隙也可以从180 nm蓝移至167 nm(Ba5P6O20),满足Nd:YAG激光六倍频(177 nm)的带隙需求[47].
对sp2杂化的平面基团,分子设计的核心思想是要消除末端O原子的非键轨道,进而有效地扩展带隙.以BO3为例,含有孤立BO3基团的Ca3(BO3)2截止边约为190 nm,末端连接一个Al原子的BABF晶体的截止边蓝移至170 nm,连接两个Be原子的KBBF晶体的截止边蓝移至151 nm.从KBBF的电子密度图(图3)上可以看出,价带顶O原子的非键轨道带宽仅为1 eV,说明绝大部分的非键轨道都被强的Be—O共价键有效地消除了;而仅连接一个Be原子的NaBeB3O6晶体价带顶O原子的非键轨道带宽约为2 eV,带隙减小,紫外截止边相应红移[48].
由于Nd:YAG激光六倍频位于177 nm,因此我们格外关注那些能透过到170 nm以下,最好能透过到150 nm以下的晶体材料.在目前的平面基团体系中,只有KBBF和CsB4O6F两种晶体在实验中证实有极佳的深紫外透过能力[49,50](图4).本课题组在2013年曾经对氟碳酸盐体系进行分子设计,发现如果能用Be或者Al元素连接CO3的末端氧原子,就可以将碳酸盐的紫外截止边扩展到160 nm左右[51,52].而对于NO3和C3N3O3体系,目前还没有太多的实验进展,需要更多的探索研究.

图3 (a)KBBF和(b)NaBeB 3O6晶体中BO 3周围的配位环境示意图;(c)KBBF和(d)NaBeB 3O 6的电子态密度[48]Fig.3.Schematic of the coordinated environments around oxygen atoms in(a)KBBF and(b)NaBeB 3O6;the density of states for(c)KBBF and(d)NaBeB 3 O6[48].

图4 含有不同功能基元的非线性光学材料的深紫外透过截止边Fig.4.Deep ultraviolet transparent edge of nonlinear optical materials containing various functional units.
3.1.2 折射率色散对相位匹配的关键作用
作为一个优良的深紫外非线性光学晶体,除了良好的深紫外透过性能以外,足够大的双折射也是一个重要的条件.由于深紫外光学材料的工作区间已经十分逼近本征透过极限,因此在200 nm以下的波段,折射率色散较大,会十分显著地影响其相位匹配性能.由于折射率的测量通常需要3 mm以上厚度的棱镜,而深紫外光源又十分短缺,因此在实验上测量完整的折射率色散曲线并不容易.这就为第一性原理计算发挥作用提供了广阔的空间.在此,我们同样以KBBF和NaBeB3O6晶体为例,分析深紫外区折射率色散对相位匹配性能的影响[48].
根据理论计算,KBBF的双折射率为0.064,NaBeB3O6的双折射率为0.08.按照之前的认识,NaBeB3O6的最短相位匹配波长会比KBBF更短,但是实际情况却远非如此.根据图5所示,KBBF的相位匹配能力可以达到200 nm以下(实验测试的最短相位匹配波长为161 nm),而NaBeB3O6的最短相位匹配波长仅为226 nm.究其原因,我们认为是NaBeB3O6晶体的折射率在深紫外区色散过大,强烈抵消了其双折射率较大的优势.折射率作为电子能带的一阶响应函数,强烈依赖于禁带两侧的电子态密度.很明显,与NaBeB3O6相比,KBBF的电子态密度有更明显的局域特征,其在深紫外波段的光学吸收函数也更低.这和KBBF中较小的折射率色散相对应.

图5 (a)NaBeB 3 O6和(b)KBBF晶体模拟的折射率色散曲线[48]Fig.5.Phase-matching capabilities for(a)NaBeB 3 O6 and(b)KBBF[48].
从更深层次的原因来看,电子态密度的分布与晶体结构有关.KBBF呈现出了明显的层状特征,电子密度局域于二维的(Be2BO3F2)共价层上;而NaBeB3O6则是三维的骨架结构,其特征骨架呈现交叉的“栅栏”特征,相应的电子密度也有更为弥散的分布空间.正是由于这个原因,NaBeB3O6在深紫外区的折射率色散更为强烈.从这个角度来看,准二维的层状结构仍然是探索深紫外非线性光学材料的最优构型.
3.1.3 NH4Be2BO3F2(ABBF)深紫外非线性光学晶体
虽然KBBF的层状结构导致其拥有优异的深紫外相位匹配能力,但是也同样带来一个问题,即晶体生长困难.KBBF晶体的(Be2BO3F2)层与层之间依靠的是K—F离子键连接,其相互作用强度比共价键至少弱了3个量级.如何增强KBBF层间的结合力,是科学界关心的一个热点问题.
为了提高KBBF的层间结合力,一个比较直接的思路就是对层间的金属阳离子进行替换.基于这种考虑,RBBF和CBBF被成功地合成和生长.但是由于Rb+和Cs+的半径较大,层间距离被进一步拉大,严重降低了BO3基团的空间堆积密度,削弱了晶体在深紫外波段的相位匹配能力.考虑到铵根离子(NH+4)与钾离子半径相近,化合价相同,因此本课题组提出用NH+4取代KBBF中的K+,在保持KBBF基本物理性能的同时,增强其层间结合力[53].
如图6所示,NH+4的引入在维持已有离子键相互作用的基础上,增加了F—H之间的氢键相互作用,层间的相互作用进一步增强.计算显示,ABBF的层间结合力是KBBF的1.24倍,沿c轴的杨氏模量是KBBF的1.56倍,这说明理论上ABBF比KBBF有更优异的生长性能.近期,中国科学院福建物质结构研究所的叶宁研究员利用水热法在实验上合成出了ABBF晶体,尽管目前晶体尺寸不大,但是具有体块特征,其层状生长习性相较于KBBF得到明显改善.这也证明我们所做的理论预测的合理性.

图6 ABBF与KBBF的空间电荷分布对比[53]Fig.6.Comparison of electronic densities between-ABBF and KBBF[53].
3.1.4 A B4O6F(A=K,Rb,Cs)系列深紫外非线性光学晶体
KBBF晶体除了层状生长习性以外,还有一个问题就是其合成原料中含有剧毒的BeO,对实验人员身体健康有潜在风险.探索不含铍的深紫外非线性光学材料是目前无机化学和功能材料领域的热点方向.在这个领域,北京师范大学的陈玲教授、中国科学院福建物质结构研究所的罗军华研究员和赵三根博士、中国科学院新疆理化技术研究所的潘世烈研究员等做出了许多卓有成效的工作,陆续合成了Ba3P3O10X(X=Cl,Br)[46],K3B6O10Cl[54],Ba3B6O11F2[55],Li4Sr(BO3)2[56],RbBa2(PO3)5[57],K3Ba3Li2Al4B6O20F[58]等一系列能够透过到深紫外区域的非线性光学材料,为新一代深紫外非线性光学晶体的发展奠定了基础.
2015年,本课题组与北京大学林建华教授合作,研究了BiB2O4F的性质,指出BO3F基元的引入有利于提高非线性光学性能[59].2017年,潘世烈课题组[60]合成了含有BO3F基团的LiB6O9F,Li2B6O9F2和Li2B3O4F3,并指出Li2B6O9F2是真正有希望相位匹配到深紫外波段的非线性光学晶体材料,为无铍深紫外非线性光学材料的发展注入了新的活力.从微观角度来看,F原子一般不倾向于较高的配位环境,因此BO3F的引入相当于生物DNA结构中的终止子,这有利于在硼酸盐体系获得低维的结构,从而在一定程度上增大材料的双折射率.
为了预测和设计可能的氟硼酸盐深紫外非线性光学材料,我们对无机晶体数据库(ICSD)进行了搜索,最终选择Ln B4O6(OH)2Cl(Ln=Ce,Pr)作为一个好的“母版”体系进行改造[61].选择该体系主要有以下几个理由:1)其晶体结构呈现准二维的构型,对深紫外非线性光学材料探索有利;2)结构中含有OH基团,且位于末端,很容易用F原子进行替换,得到BO3F基团;3)该化合物是一个非中心对称的化合物,粉末倍频效应与KB5晶体相当,具有一定的结构改造潜力.对Ln B4O6(OH)2Cl(Ln=Ce,Pr)的结构改造主要考虑到以下几个方面:1)稀土元素对深紫外透过不利,需要用碱金属或者碱土金属进行替换;2)孤立的Cl−对能带的贡献主要集中在价带顶部,对提升深紫外透过性能同样不利,需要直接去掉,同时由碱金属/碱土金属位置补偿电荷;3)OH−替换成F−,这样可以将BO3(OH)基团替换成BO3F,有利于增强基团的各向异性,提高非线性光学效应,同时F原子的引入也有利于拓宽带隙,有利于深紫外波段的透过;4)改造后的化合物对称性应该尽可能的高,这样对实际应用有利.
基于以上思想,经过合理设计与优化,获得了两种新型化合物BaB4O6F2和KB4O6F-I.声子谱计算证实这两种材料没有虚频,有可能在实验上合成出来;光学性质计算显示它们的相位匹配能力都不错,已经非常接近KBBF.但是这两种材料对称性太低,是单轴晶体(Cc空间群),这可能会对实际应用造成不利影响.为此,我们从空间对称性的角度出发,重新设计获得了KB4O6F-II结构[62].对F原子做改动,新优化的KBF-II结构属于三方的P31c空间群(图7),对称性得到了提高.值得一提的是,我们在文章中预测了B3O6六元环和BO3F四面体共顶点连接这一新颖连接方式,可以得到优异的深紫外非线性光学性能.计算结果显示,KBF-II具有优良的深紫外透过区间(截止边161 nm)、足够大的非线性光学系数(d22=−0.51 pm/V)和适中的双折射率(0.098),具有在深紫外区间实现相位匹配的能力,能满足Nd:YAG六倍频的需求.一旦在实验上被合成,则有可能成为下一种实用的深紫外非线性光学晶体.
在我们的理论设计工作发表前后,中国科学院新疆理化技术研究所的潘世烈课题组发现了NH4B4O6F(ABF),RbB4O6F(RBF),CsB4O6F(CBF)晶体等几种新型氟硼酸盐[50,63,64],其结构存在B3O6F和BO3共同连接,或B3O6和BO3F共同连接的新颖连接方式,从而在实验上独立验证了我们的预测.他们通过合理地选择碱金属离子,还成功得到三方晶系的化合物CsKB8O12F2(CKBF)和CsRbB8O12F2(CRBF),实现了阴离子基团的优化平面排列[64].2018年,中国科学院福建物质结构研究所叶宁课题组和本课题组合作研发了首例碱土金属氟硼酸盐非线性光学材料M2B10O14F6(M=Ca,Sr),同样具备200 nm以下的深紫外谐波输出能力[65].这些结果都证明氟硼酸盐体系是一个非常有潜力的新型深紫外非线性光学材料体系.

图7 (a)KBF-I到KBF-II的基团演化示意图;(b),(c)KBF-II的晶体结构示意图[62]Fig.7.(a)Diagram of structural evolution from KBF-I to KBF-II;(b),(c)diagram of crystal structure of KBF-II[62].
3.2 中红外波段非线性光学探索
中红外波段激光以其高亮度、良好的相干性和极高的空间分辨率等特点在红外对抗、激光制导、红外测距、分子光谱、医学诊疗、地球遥感探测等军事和民用领域有着广泛的应用.OPO,OPA或差频(DFG)等非线性频率转换技术,是产生中红外激光输出的主要手段[66].此外,中红外光区还是远程通讯的重要手段,许多研究领域所需要的激光红外光谱仪的诞生也有赖于新型优良中红外波段非线性光学晶体的出现.目前,研究最多的中红外非线性光学晶体材料有AgGaS2,AgGaSe2和ZnGeP2等.AgGaS2和AgGaSe2晶体已经实现了商业化应用,但是这两种材料抗激光损伤阈值比较低 (小于100 MW/cm2),无法应用于高功率的激光输出.ZnGeP2晶体非线性光学系数大,相位匹配区间宽,是目前3—5µm波段激光输出的最佳选择;但是其带隙较窄,对1µm的抽运光双光子吸收严重;非本征缺陷引起ZnGeP2晶体的光吸收和光散射,造成晶体在2µm处透过率低,同时8—10µm存在多声子吸收.因此,迫切需要研发具有高激光损伤阈值和强非线性光学效应的新型中红外非线性光学晶体.但是,激光损伤阈值(本征地决定于晶体带隙)与非线性光学效应存在着此消彼长的矛盾[33].对于新型中红外非线性光学晶体的研究,目前主要集中在实现大的非线性光学系数(dij>10dKDP或dij>0.5dAgGaS2)和高的抗激光损伤阈值(即大带隙Eg>3.0 eV)的平衡上[33,67,68].第一性原理方法可以通过计算非线性光学系数和晶体带隙,为材料筛选提供初步判断,提高新材料的研发速度.
3.2.1 硫属化合物中各种功能基团对红外非线性光学性能的影响
近年来,科学家们对新型硫属红外非线性光学材料进行了卓有成效的探索.作为非线性光学晶体,其前提是具有非中心对称的结构.虽然目前科学家们还不能控制原子或分子的空间排列,但是通过引入非中心对称的结构基元,可以更大概率地获得非中心对称的化合物.这些非中心对称的结构基元包括八面体配位的d0,d10过渡金属,含有孤对电子的主族阳离子,以及含有共轭π键的平面基团(图8)等.这些基团会显著影响红外非线性光学晶体材料的性质,如何有效区分这些基团对晶体物性的影响,优化和改善晶体的性质,是探索新型非线性光学材料的关键问题.下面分别对这几种基团类型进行简单总结和分析[69].
1)平面基团
平面基团的典型代表有两类,一类是含有共轭π键的平面基团,如BS3,B3S6等.硼硫基团在电子结构上与硼氧基团有一定相似性,但是硼硫化合物的稳定性远不如硼氧化合物.一般来说,硼硫化合物对空气和水分比较敏感,必须放在高纯氩气的手套箱内保存,因此并不适合作为实用的非线性光学晶体.实验上也仅有少数几例硼硫化合物的非线性光学效应被研究过,包括Ba3(BS3)(SbS3),Zn0.2Ba2B2S5.2等.在此我们不再赘述.另一类平面基团是以d10金属元素为中心的平面基团,如ZnS3,HgSe3等.2016年,中国科学院理化技术研究所课题组姚吉勇研究员[70]报道了一种新型的红外非线性光学材料BaHgSe2,这种材料表现出了较强的非线性光学响应(1.5dAgGaS2).第一性原理计算证明平面(HgSe3)基团对非线性光学系数的贡献超过75%,这为新型硫族红外非线性光学材料的探索提供了新的思路.
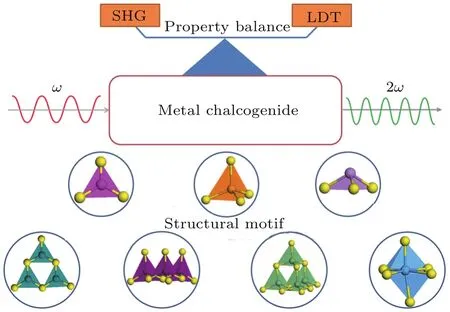
图8 红外金属硫族化合物非线性光学晶体材料中的功能基团与评价标准[69]Fig.8.Functional structural motifs and descriptors in mid-infrared metal chalcogenides NLO materials[69].
2)二阶姜-泰勒效应基团
姜-泰勒效应(Jahn-Teller eff ect)是指电子在简并轨道中的不对称占据会导致分子的几何构型发生畸变,从而降低分子的对称性和轨道的简并度,使体系的能量进一步下降.与严格意义的基态电子简并态(一阶姜-泰勒效应)相比,能量相近的电子轨道(二阶姜-泰勒效应)产生的畸变更大,相应基团的偶极矩也就更大,因此可以显著改变材料的非线性光学响应.一般而言,姜-泰勒效应在氧化物八面体中最为典型.按照畸变类型划分,可以分为C2,C3,C4三类畸变,分别对应着二次轴、三次轴和四次轴的畸变方向.在硫族化合物中,由于M—S键较弱,金属的配位数较高,对姜-泰勒效应的定义也可以不局限于六配位八面体[71].我们利用第一性原理计算了TiP2S6的非线性光学效应,发现其非线性效应较大(d15=15.45 pm/V),与AgGaS2相当[33].美国西北大学的Kanatzidis教授等[72]合成了含有ZrSe7基团的A ZrPSe6(A=K,Rb,Cs)化合物,非线性光学效应也超过了AgGaSe2的10倍.但是由于姜-泰勒效应理论上是存在于电子的占据态与非占据态之间的一种效应,因此难以得到很大带隙,通常情况下都小于3.0 eV.
3)孤对电子基团
孤对电子效应是指金属的部分价电子未与其他原子成键,而是分布在某一个局域方向上,如IO3,TeO4,AsS3,SbS3等.这样的基元一般都具有较大的极性,从而在外场扰动有比较大的非线性光学响应.Kanatzidis等[73,74]合成了含有孤对电子基团的LiAsS2和γ-NaAsSe2,其非线性光学效应分别达到了AgGaSe2的10倍和75倍,和我们理论计算的结果一致.值得注意的是,有一种特殊的化合物Cs2TeS2,其中的TeS2基团含有两对孤对电子(5s25p2),其非线性光学系数超过了100 pm/V,同样证实了孤对电子可显著增强非线性光学效应[69].究其原因,孤对电子一般分布于价带的顶部,可以显著增加价带顶的电子态密度,因而对非线性光学效应做出贡献.正是因为如此,含有孤对电子的化合物的带隙通常比较窄,激光损伤阈值比较低.以Ag3SbS3为例,其损伤阈值仅有9 MW/cm2,约为同等条件下AgGaS2的1/4[75].
4)四面体和超级四面体基团
含有四面体基团的金属硫族化合物是非线性光学材料的研究热点.近年来,陆续发现了多种新型材料,如Na2ZnGe2S6等[76],Na2BaGeS4[67],BaLi2GeS4[68],[A3X][Ga3PS8](A=K,Rb;X=Cl,Br)[77].这些材料兼具较宽的带隙和较强的非线性光学效应,具有一定的实用价值.其中具有类金刚石的化合物表现出了特别的应用潜力,如Li2Cd GeS4,Li2Cd SnS4[78]等.为此,本课题组利用第一性原理方法,系统地研究了类金刚石体系中红外非线性光学性能的构效关系,给出了类金刚石体系的化合物族谱,为今后大规模、高通量地探索新型红外非线性光学材料提供了理论支持和帮助[79].下面进行详细介绍.
3.2.2 基于类金刚石构型的非线性光学材料探索
从晶体化学的角度看,类金刚石构型可以看作是闪锌矿和纤锌矿(图9)的衍生物.对标准的类金刚石构型,需要满足以下几个基本特征:1)结构的阴阳离子都是四配位构型,且都呈现近似密堆积构型;2)所有离子的平均价电子浓度为4;3)所有阴离子的平均价电子浓度为8[80].常见的黄铜矿型化合物即属于该结构体系.按照阳离子的种类划分,类金刚石构型化合物可以分为二元、三元和四元三种.可以看出,在类金刚石构型中,所有的四面体基团朝向基本一致,呈现宏观的偶极矩方向,属于极性空间群,这有利于获得较大的非线性光学效应;同时,四面体基团中原子之间的化学键为sp3杂化,可产生较大的带隙.
类金刚石化合物从二元演变到四元,其结构和组分非常丰富.我们按照化学计量比的规则,给出了类金刚石结构的族谱,如图10所示.从图10可以看出,目前实验已经发现的类金刚石结构主要集中在三元体系和部分四元体系.在未知的四元体系中,还有着非常广阔的探索空间.2017年,中国科学院新疆理化技术研究所潘世烈课题组[81]合成了多种新型四元类金刚石材料,如Li2ZnSiS4[82],Li4HgGe2S7[83],Li2Hg M S4(M=Si,Ge,Sn)等,其优异的非线性光学性质得到了初步验证,也证实了我们的理论预测.
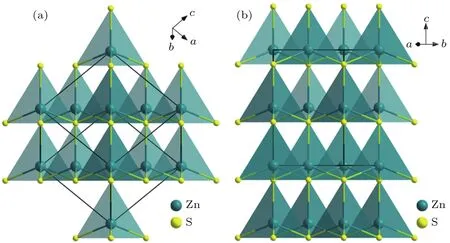
图9 晶体结构图 (a)闪锌矿Zn S;(b)纤锌矿ZnSFig.9.Crystal structures:(a)Sphalerite(α-Zn S);(b)wurtzite(β-ZnS).
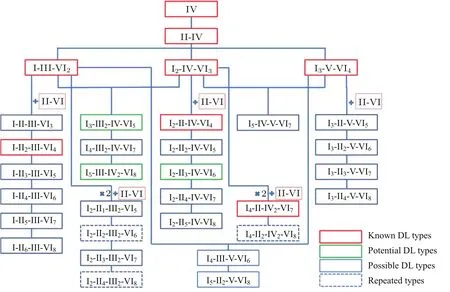
图10 常规型类金刚石硫族化合物族谱图(红色矩形代表实验上已获得的类金刚石结构,绿色矩形代表非常可能存在的类金刚石结构,蓝色矩形代表有一定可能存在的类金刚石结构,虚线矩形代表重复的类金刚石结构[79])Fig.10.Family tree of normal diamond-like chalcogenides.the red boxes represent the DL structures that have been synthesized in experiments;the green boxes represent the potential DL structures which have been not synthesized yet,but have similar DL oxides or chalcogenides discovered in experiments;the cyan boxes represent the possible DL structures which are waiting for synthesis in experiments;the dotted boxes represent the repeated DL structures which are the same as other DL structures[79].
除了标准的类金刚石构型化合物,还有一类缺陷型的类金刚石化合物,如HgGa2S4,Hg2GeSe4,InPS4,LiZnPS4,其主要特点是结构中的部分阳离子位置出现缺失,而另一部分阳离子提高化合价以维持电荷平衡.以HgGa2S4为例(图11),在AgGaS2晶体结构的基础上,一半Ag+缺失,另一半Ag+替换成Hg2+,同时Hg2+和Ga3+之间有部分易位替换,晶体的空间群从I-42m变成了I-4.由于部分阳离子缺失,晶体中的平均价电子浓度不再等于4,而是大于4.实验发现HgGa2S4的带隙与AgGaS2相差不多,约为2.84 eV,但是非线性光学系数却增加到了31.5 pm/V,约为AgGaS2的2.5倍[79].这种反常的现象激发了我们的研究兴趣.为此,我们计算了HgGa2S4的电子能带结构(图12),发现HgGa2S4和AgGaS2的能带结构有很大不同,最关键的不同是HgGa2S4中含有大量的未成键局域电子,且其空间分布与HgGa2S4中的最高占据态电子的空间分布高度重叠.因此,与不含有局域电子的AgGaS2相比,HgGa2S4在价带顶的电子态密度明显提高,对非线性光学效应的增强起到了主要贡献.
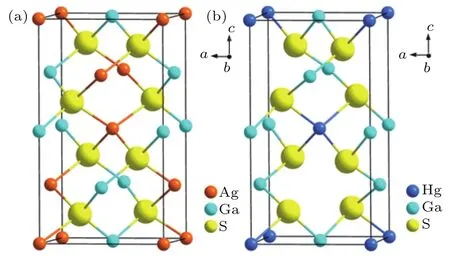
图11 晶体结构对比 (a)AgGaS2;(b)HgGa2S4Fig.11.Comparison of crystal structure:(a)AgGaS2;(b)HgGa2 S4.

图12 HgGa2 S4晶体的(a)能带结构、(b)电子态密度、(c)局域电子密度和(d)最高占据态轨道示意图Fig.12.(a)Band structure,(b)density of states,(c)electron localization function(ELF)map,(d)schematic of highest occupied molecular orbitals(HOMO)of HgGa2S4.
为了验证我们的猜想是否正确,本课题组和姚吉勇课题组合作合成了缺陷类金刚石材料Hg2GeSe4.实验证实其非线性光学效应约为AgGaSe2的2倍,且增强机理与HgGa2S4类似,说明我们的预测是正确的.除此之外,在其他缺陷型类金刚石化合物,如Zn3(PS4)2[33],InPS4[84],Ga2S3[85]中,也证实增强了非线性光学效应.
除此之外,近5年报道的可能的红外非线性光学晶体材料超过了50种,我们在之前的综述文章中进行了系统的总结.但是遗憾的是,这些化合物多停留在小晶粒和粉末样品阶段,未见大尺寸晶体的生长报道.一个红外非线性光学晶体(硫族和磷族化合物)最后要得到实际应用,关键是要获得大尺寸、高质量的体块晶体.目前看来,这需要材料是同成分熔融的,才能采用坩埚下降法生长大尺寸的晶体.目前通过第一性原理的方法来预测晶体是否具有同成分熔融的性质还十分困难,因此需要理论和实验的通力合作.
3.2.3 基于卤化物的红外非线性光学探索
卤族化合物材料具有配位环境多样、带隙较宽、激光损伤阈值高的特点,在中红外波段也具有一定的应用潜力.2013年,本课题组系统地总结了卤素化合物的配位类型,阐明了微观结构与光学性能之间的关系,指出具有四面体型的、三角锥状的和一维链状的混合卤素结构能够呈现出相对均衡的中红外非线性光学性能,既可保证足够的带隙,又能维持较大的倍频效应[28].武汉大学的秦金贵、陈兴国教授课题组与本课题组合作,在新型卤族非线性光学材料实验探索中取得了丰硕的成果,近年来陆续合成出了含有杂化卤素的Cs2HgI2Cl2等[86],Rb2Cd Br2I2[87]化合物.其中Rb2Cd Br2I2同时具有大的带隙(>3.0 eV)和较强的非线性光学效应(约4dKDP),在中红外波段具有潜在的应用价值.
3.3 太赫兹波段的非线性光学材料探索
目前,对于太赫兹波段的新型非线性光学晶体的探索还处于初步阶段,理论和计算方面的研究不多.本课题组曾经计算过OH1晶体和PSDCM-I晶体的静态非线性光学系数,与2.09µm测到的实验值基本符合[88].Kwon课题组[89]也计算过OH1和DAT2晶体的零频一阶超极化率,与实验值基本符合.但是值得注意的是,现有的计算还局限在只考虑电子贡献的情况下,对太赫兹波段下晶体中声子与光子非线性耦合过程的研究十分匮乏.因此,对太赫兹晶体光学性质的准确计算是第一性原理方法亟待发展的一个方向.
4 具有新颖微观结构基元的非线性光学材料探索
除了应用于深紫外、中远红外和太赫兹区的非线性光学晶体,我们还重点关注了新颖的非线性光学活性基团以及基团之间的组合连接方式.通过这些有益的尝试,可以进一步拓展非线性光学材料研究的空间,为新型非线性光学晶体研究提供有力的支持.在此,举3个例子,分别是含有离域π键的氰尿酸盐体系、具有定域π键的过氧酸盐体系以及组合了多种功能基团的化合物.
4.1 氰尿酸盐非线性光学晶体
氰尿酸盐体系是一个长期被忽略的非线性光学材料体系.2014年,德国的Meyer等[90]创造性地采用真空封管合成方法,合成了一系列的含有(C3N3O3)3−功能基团的氰尿酸盐晶体,并发现其中部分晶体具有二阶非线性光学响应特征.为了更好地分析和展望该体系的研究前景,我们利用第一性原理方法对Sr3(C3N3O3)2(SCY)化合物做了细致研究[38].
(C3N3O3)3−基团与(B3O6)3−是等电子体,sp2杂化轨道是它们的共同特征.但是,由于原子种类的不同,其π键轨道上的电子分布有很大差别.如图13所示,B3O6中的B原子仅有3个价电子,因此仅能提供一个空的p轨道参与形成π键,无法提供额外的p电子,而其中的O原子则可以提供2个p电子;C3N3O3中的C原子有4个价电子,在sp2杂化下,不仅可以提供一个空的p轨道,而且可以提供1个p电子参与形成π键,而N原子也可以提供1个p电子参与形成π键,因此在C3N3O3平面基团中,p电子分布更为平均,相应的共轭π键特征也更为明显.在电子局域函数图上可以看出,C3N3六元环之间有6个均匀分布的高亮区域,猜测应该是对应着6个均匀分布的p电子,而B3O3六元环中的6个p电子明显更靠近O.计算显示,SCY的非线性光学系数d22为3.93 pm/V,约为BBO的2倍.实空间原子切割证实(C3N3O3)3−基团的贡献超过了90%,这与BBO中B3O6基团的绝对贡献相一致.Meyer教授的实验结果也证实SCY在800 nm下的倍频响应高于BBO[90],这和我们的计算结果相符合.

图13 B3O6和C3N 3O3基团中的共轭π电子分布对比示意图Fig.13.Conjugatedπelectrons distribution in B 3O6 and C3N 3O3 groups.
值得一提的是,Meyer等[90]报道的SCY的带隙为2.9 eV,这个结果可能不太准确.如果SCY的带隙太窄,那么它对于倍频光(400 nm)基本上是全吸收的,应该不会有倍频信号被观察到.我们采用杂化泛函计算的SCY的带隙为5.57 eV,与H3C3N3O3的带隙值5.53 eV比较一致.最近,印度科学家Divya等[91]合成了Sr(C3N3O3H2)2·4H2O化合物,实验测得的带隙为4.9 eV,也更接近我们计算的结果.目前,SCY中的C3N3O3基团仍然是孤立的,其末端O原子的非键轨道并没有消除.如果能通过引入其他共价原子的方式消除其非键轨道,有望将氰尿酸盐的透过波段拓展到深紫外区间.近日,我们和中国科学院理化技术研究所的夏明军博士合作,合成了一种新的含有C3N3O3基团的化合物K6Cd3(C3N3O3)4,其实验带隙为5.23 eV.理论计算显示其非线性光学系数d14为1.07 pm/V,约为KDP的3倍[92].
4.2 定域π键对非线性光学效应的影响
定域π键也是被大家长期忽略的一种基团,主要原因是其在无机化合物中出现的概率比较低.无机化合物中典型的定域π键有氧氧双键(O=O)、硫硫双键(S=S)、硒硒双键(Se=Se).在此,我们主要关注第一种.该工作是和中国科学院福建物质结构研究所的叶宁研究员合作完成的[93].
在化合物K3[V(O2)2O]CO3中,同时含有两种共轭π键基团:离域的CO3和定域的O=O.实验上观测到该化合物的粉末倍频效应极大,约为KDP的20倍.如何解释这种巨大倍频效应的来源呢?对此,我们首先计算了化合物的最高占据态轨道(HOMO)和最低的未占据态轨道(LUMO),发现其占据态轨道绝大部分是O=O双键中平行排列的p电子,而未占据态轨道主要是V的d电子(图14).电子局域函数图上也可以看出在两种共轭π键的周围存在着明显的未成对电子,这将对非线性光学效应起到重要作用.K3[V(O2)2O]CO3有两个比较大的非线性光学系数分量,分别是d11和d24.将非线性光学系数的分波贡献与电子态密度进行比对,发现d11的主要贡献来源于CO3中的O原子,而d24的主要贡献则来源于O=O中的O原子,这说明定域π键和离域π键的作用是截然不同的.O=O的能带位置更高,对决定带隙的大小起到了决定作用.这也和陈玲课题组[94]在Ba4Ga2(µ-S2)S6中S=S双键决定带隙的结论一致.

图14 K 3[V(O2)2 O]CO 3晶体的(a)HOMO,(b)LUMO,(c)O=O的局域电子密度;(d)CO 3的局域电子密度[93]Fig.14.(a)HOMO,(b)LUMO,electron localized functions(ELF)distribution of(c)O=O dimer and(d)the CO3 plane[93]of K 3[V(O2)2O]CO3.
4.3 新型基团组合方式的研究
Bi3TeBO9是中国科学院理化技术研究所夏明军博士等[95]于2016年首次合成的新型硼酸盐化合物.在它的晶体结构中同时含有3种不同的功能基团:平面共轭基团BO3、具有孤对电子效应的BiO6基团和具有姜-泰勒效应的TeO6基团.其粉末倍频效应也达到了KDP的20倍,是目前已知硼酸盐化合物中最大的.实空间原子切割分析表明,该化合物巨大的SHG效应主要来源于畸变的TeO6基团.后来,波兰的Piasecki等[96]和德国的Hillebrecht等[97]也研究了该化合物,证实了其非线性光学效应的来源.
类似这种多种功能基团组合的现象也在我们研究的其他化合物中有所体现,如Bi3TeO6OH(NO3)2同时包含了BiO3,TeO6和NO3基团[98],Pb2(NO3)2(H2O)F2同时包含孤对电子Pb2+,NO3和扩宽带隙的F−[99],Cd5(BO3)3Cl同时含有d10电子组态的Cd2+,BO3和Cl−等[100].功能基元丰富多样的连接和组合方式,为新型非线性光学材料的探索提供了广阔的平台,也为无机功能材料的发展提供了有利的支持.
5 非线性光学晶体中的材料基因工程
在20多年前,仅从化合物的化学组成出发计算预测晶体结构被认为是不可能完成的,但是,随着21世纪以来高性能计算平台硬件和软件的发展,这已成为可能.因此,利用计算机强大的计算预测能力,结合材料计算分析工具与构效信息,建立材料性能的精确模型,可望大大缩短材料的开发周期.2011年,奥巴马宣布了一项重大计划即“材料基因组计划”,此计划一经提出,便迅速席卷全球,引起了材料界研究人员的广泛关注[101].由于在锂离子电池、高熵合金、热电材料、储氢材料、金属有机框架材料、催化材料等多种功能材料领域都有着广泛的应用,非线性光学晶体的“基因工程学”探索和研究成为大势所趋.在陈创天院士提出的紫外硼酸盐分子设计专家系统的基础上,我们进一步拓展了其应用领域,发展了基于第一性原理的非线性光学晶体设计系统,如图15所示.其主要研究思路是:把第一性原理计算工具与具有超强计算能力和超大存储容量的大规模并行计算平台紧密结合,快速准确地确定非线性光学晶体的关键光学性质,如倍频系数、带隙、透过率、折射率等,实现结构与性能关系的快速识别.利用晶体结构和各种物性数据库,进行数据整理和挖掘,获得非线性光学晶体的构效关系(“材料基因”),总结选型规律,帮助实验快速高效地基于“材料基因”搜索设计新型非线性光学晶体.

图15 基于第一性原理的非线性光学晶体分子设计专家系统路线图Fig.15.Flow chart for the molecular design system of nonlinear optical crystals based on fi rstprinciple theory.
材料结构的预测是材料设计迈向实用化的关键步骤,结构的准确预测能够了解材料在服役条件下的行为,同时为按预先设定的物理性能成功制备新材料提供有效的途径.目前国外的主流手段是在无机晶体数据库中进行高通量的筛选,而没有过多地考虑功能基元的贡献,造成计算资源的浪费.另外,受限于DFT的发展和计算资源的短缺,目前材料基因组计划的描述符还是以单胞参数和能量为主,对光学性质的研究比较少,而这恰恰是非线性光学晶体最为关心的.第一性原理方法在新型非线性光学材料探索中可着重于以下几个方向.
1)准确的电子能带结构计算
由于非线性光学效应涉及到外场对电子能带的二阶和高阶微扰,因此对电子能带结构的计算精度要求很高.目前的准静态计算方法和附加频率色散的计算方法的精度都不高,因此有必要继续发展新的计算方法.另一方面,非线性光学系数的准确预测离不开对晶体带隙的准确计算.鉴于LDA和GGA泛函都会显著地低估带隙,因此特别需要发展计算速度更快的杂化泛函来准确地预测材料带隙.预测带隙非常准确的GW方法计算成本太高,短期内可能还无法实现大规模使用.
2)范德瓦耳斯作用体系和强相关体系中的光学性质
除了传统的体块非线性光学晶体,近期实验上也在一些低维材料(MoS2[102],h-BN[103],GaSe[104])和拓扑材料(TaAs,TaP)[105]中观察到了极强的非线性光学信号.这些材料中的非线性光学效应来源和潜在应用也是一个值得关注的方向.由于这些材料的高质量样品制备比较困难,因此很有必要先在理论上对其进行计算研究.
对于低维材料,首先要解决的是非线性光学系数的定义问题.在体块材料非线性光学系数χijk的定义中,有一个体积的概念,但是在二维层状材料中这一物理参数应该如何处理,目前还没有定论.另外低维材料中的激子效应十分明显[106],也需要在理论计算中考虑.对于强关联的拓扑材料,一个亟待解决的问题就是非线性光学系数的重新定义.在一些拓扑半金属和拓扑绝缘体材料中,已经没有明确的带隙概念,因此无法采用已有的物理公式进行处理.另外拓扑材料中的自旋轨道耦合效应一般比较强烈,这也是目前的计算公式没有考虑的.
3)晶格振动与光学性质之间的关系
一方面,目前的非线性光学系数计算公式中,仅仅考虑了电子的贡献而没有考虑声子的贡献.对于宽禁带的氧化物材料,这一近似是合理的,因为声子振动的能量(一般小于200 meV)远远小于带隙值和光子能量.但是对于工作在太赫兹波段的非线性光学晶体,光子能量已经很接近声子能量,此时声子的贡献就不能忽略了.
另一方面,晶格振动对非线性光学晶体的红外吸收有重要影响.目前对晶体的红外透过和晶格振动之间的关系的认识还不够清晰,一些课题组在实验中采用粉末红外光谱估计晶体的红外截止边的做法也是不可取的.因此非常有必要建立一套高通量计算材料晶格振动的方法,来详细研究晶格振动与红外透过之间的关系.这也将有助于我们进一步开发性能优秀的红外非线性光学晶体.
总之,第一性原理方法可以在非线性光学材料的研发过程中扮演重要的角色,现阶段依然任重而道远.
6 总结与展望
非线性光学材料经过半个世纪的发展,已经积累了大量成功的经验.现阶段的主要任务是既要将已有的晶体材料长好,同时又要继续研发性能优良的新晶体.具有良好性能的非线性光学材料的成功设计离不开对构效关系的深刻认识和对晶体结构的准确预测,特别是对于二阶非线性光学材料光物理性能的计算模拟.相信随着结构预测理论方法和计算技术、计算资源的发展,第一性原理方法将在这一领域发挥越来越重要的作用.通过将理论模拟与“结构搜索”、“化学合成”、“粉末倍频效应测试”和“单晶生长”等实验手段紧密结合,建立了快速高效的非线性光学材料分子设计专家系统.发展和完善这一基于分子工程学基础的专家系统,将能加快非线性光学晶体的研究步伐,提升其自主创新水平.同时,将非线性光学效应从传统的体块晶体拓展到低维材料、拓扑材料,也将是未来第一性原理在非线性光学领域的重要任务.
感谢台湾淡江大学李明宪教授,山东大学王继扬、张怀金、于浩海教授,武汉大学秦金贵、陈兴国教授,中国科学院福建物质结构研究所罗军华研究员、赵三根博士、叶宁研究员,中国科学院理化技术研究所姚吉勇研究员、夏明军博士的讨论与合作.
[1]Savage N 2007 Nat.Photonics 1 83
[2]Garmire E 2013 Opt.Express 21 30532
[3]Chen C T,Wu B C,Jiang A D,You G M 1985 Sci.China B 28 235
[4]Chen C T,Wu Y C,Jiang A D,Wu B C,You G M,Li R K,Lin SJ 1989 J.Opt.Soc.Am.B:Opt.Phys.6 616
[5]Xu B,Liu L,Wang X,Chen C,Zhang X,Lin S 2015 Appl.Phys.B 121 489
[6]Bierlein J D,Vanherzeele H 1989 J.Opt.Soc.Am.B:Opt.Phys.6 622
[7]Zhu S,Zhu Y Y,Ming N B 1997 Science 278 843
[8]Lu Y L,Wei T,Duewer F,Lu Y,Ming N B,Schultz P G,Xiang X D 1997 Science 276 2004
[9]Lu Y Q,Zhu Y Y,Chen Y F,Zhu S N,Ming N B,Feng Y J 1999 Science 284 1822
[10]Wang L,Xing T,Hu S,Wu X,Wu H,Wang J,Jiang H 2017 Opt.Express 25 3373
[11]Wang S,Zhang X,Zhang X,Li C,Gao Z,Lu Q,Tao X 2014 J.Cryst.Growth 401 150
[12]Lin X,Zhang G,Ye N 2009 Cryst.Growth Des.9 1186
[13]Yao J Y,Mei D J,Bai L,Lin Z S,Yin W L,Fu P Z,Wu Y C 2010 Inorg.Chem.49 9212
[14]Wang S,Dai S,Jia N,Zong N,Li C,Shen Y,Yu T,Qiao J,Gao Z,Peng Q,Xu Z,Tao X 2017 Opt.Lett.42 2098
[15]Yang F,Yao J Y,Xu H Y,Zhang F F,Zhai N X,Lin Z H,Zong N,Peng Q J,Zhang J Y,Cui D F,Wu Y C,Chen C T,Xu Z Y 2015 IEEE Photonics Technol.Lett.27 1100
[16]Li Y,Wu Z,Zhang X,Wang L,Zhang J,Wu Y 2014 J.Cryst.Growth 402 53
[17]Liu P,Zhang X,Yan C,Xu D,Li Y,Shi W,Zhang G,Zhang X,Yao J,Wu Y 2016 Appl.Phys.Lett.108 011104
[18]Liu P,Xu D,Li Y,Zhang X,Wang Y,Yao J,Wu Y 2014 EPL 106 60001
[19]Halasyamani P S,Zhang W 2017 Inorg.Chem.56 12077
[20]Zhou M,Kang L,Yao J,Lin Z,Wu Y,Chen C 2016 Inorg.Chem.55 3724
[21]Kong F J,Jiang G 2009 Physica B:Conden.Matter.404 2340
[22]Clark S J,Segall M D,Pickard C J,Hasnip P J,Probert M J,Refson K,Payne M C 2005 Z.Kristallogr.220 567
[23]Rashkeev S N,Lambrecht W R L,Segall B 1998 Phys.Rev.B 57 3905
[24]Perdew J P,Wang Y 1992 Phys.Rev.B 45 13244
[25]Marques M A L,Gross E K U 2004 Annu.Rev.Phys.Chem.55 427
[26]Onida G,Reining L,Rubio A 2002 Rev.Mod.Phys.74 601
[27]Lin J,Lee M H,Liu Z P,Chen C T,Pickard C J 1999 Phys.Rev.B 60 13380
[28]Kang L,Ramo D M,Lin Z,Bristowe P D,Qin J,Chen C 2013 J.Mater.Chem.C 1 7363
[29]Lin Z S,Kang L,Zheng T,He R,Huang H,Chen C T 2012 Comput.Mater.Sci.60 99
[30]He R,Lin Z S,Zheng T,Huang H,Chen C T 2012 J.Phys.Condens.Matter 24 145503
[31]He R,Huang H,Kang L,Yao W,Jiang X,Lin Z,Qin J,Chen C 2013 Appl.Phys.Lett.102 231904
[32]Lin Z S,Jiang X X,Kang L,Gong P F,Luo S Y,Lee M H 2014 J.Phys.D:Appl.Phys.47 253001
[33]Kang L,Zhou M,Yao J,Lin Z,Wu Y,Chen C 2015 J.Am.Chem.Soc.137 13049
[34]Lin Z S,Lin J,Wang Z Z,Chen C T,Lee M H 2000 Phys.Rev.B 62 1757
[35]Chen C T,Wu Y C,Li R K 1989 Int.Rev.Phys.Chem.8 65
[36]Zhang J,Kang L,Lin T H,Jiang X,Gong P,Lee M H,Lin Z 2015 J.Phys.Condens.Matter 27 85501
[37]Lee M H,Yang C H,Jan J H 2004 Phys.Rev.B 70 235110
[38]Liang F,Kang L,Zhang X,Lee M H,Lin Z,Wu Y 2017 Cryst.Growth Des.17 4015
[39]Jiang X,Zhao S,Lin Z,Luo J,Bristowe P D,Guan X,Chen C 2014 J.Mater.Chem.C 2 530
[40]Lan H,Liang F,Lin Z,Yu H,Zhang H,Wang J 2017 Int.J.Opt.207 1
[41]Lan H,Liang F,Jiang X,Zhang C,Yu H,Lin Z,Zhang H,Wang J,Wu Y 2018 J.Am.Chem.Soc.140 4684
[42]Liu G,Wang G,Zhu Y,Zhang H,Zhang G,Wang X,Zhou Y,Zhang W,Liu H,Zhao L,Meng J,Dong X,Chen C,Xu Z,Zhou X J 2008 Rev.Sci.Instrum.79 023105
[43]Cyranoski D 2009 Nature 457 953
[44]Pan F,Shen G Q,Wang R J,Wang X Q,Shen D Z 2002 J.Cryst.Growth 241 108
[45]Zhang X,Wang L,Zhang S,Wang G,Zhao S,Zhu Y,Wu Y,Chen C 2011 J.Opt.Soc.Am.B:Opt.Phys.28 2236
[46]Yu P,Wu L M,Zhou L J,Chen L 2014 J.Am.Chem.Soc.136 480
[47]Zhao S,Gong P,Luo S,Bai L,Lin Z,Tang Y,Zhou Y,Hong M,Luo J 2015 Angew.Chem.Int.Ed.54 4217
[48]Jiang X,Luo S,Kang L,Gong P,Huang H,Wang S,Lin Z,Chen C 2015 ACS Photonics 2 1183
[49]Chen C T,Liu L J,Wang X Y 2014 Physics 43 520(in Chinese)[陈创天,刘丽娟,王晓洋 2014物理43 520]
[50]Wang X,Wang Y,Zhang B,Zhang F,Yang Z,Pan S 2017 Angew.Chem.Int.Ed.56 14119
[51]Zou G,Ye N,Huang L,Lin X 2011 J.Am.Chem.Soc.133 20001
[52]Kang L,Lin Z,Qin J,Chen C 2013 Sci.Rep.3 1366
[53]Kang L,Luo S,Peng G,Ye N,Wu Y,Chen C,Lin Z 2015 Inorg.Chem.54 10533
[54]Wu H,Pan S,Poeppelmeier K R,Li H,Jia D,Chen Z,Fan X,Yang Y,Rondinelli J M,Luo H 2011 J.Am.Chem.Soc.133 7786
[55]Yu H,Wu H,Pan S,Yang Z,Su X,Zhang F 2012 J.Mater.Chem.22 9665
[56]Zhao S,Gong P,Bai L,Xu X,Zhang S,Sun Z,Lin Z,Hong M,Chen C,Luo J 2014 Nat.Commun.5 4019
[57]Zhao S,Gong P,Luo S,Bai L,Lin Z,Ji C,Chen T,Hong M,Luo J 2014 J.Am.Chem.Soc.136 8560
[58]Zhao S,Kang L,Shen Y,Wang X,Asghar M A,Lin Z,Xu Y,Zeng S,Hong M,Luo J 2016 J.Am.Chem.Soc.138 2961
[59]Cong R,Wang Y,Kang L,Zhou Z,Lin Z,Yang T 2015 Inorg.Chem.Front.2 170
[60]Zhang B,Shi G,Yang Z,Zhang F,Pan S 2017 Angew.Chem.Int.Ed.56 3916
[61]Belokoneva E L,Stefanovich S Y,Dimitrova O V,Ivanova A G 2002 Zh.Neorg.Khim.47 370
[62]Liang F,Kang L,Gong P,Lin Z,Wu Y 2017 Chem.Mater.29 7098
[63]Shi G,Wang Y,Zhang F,Zhang B,Yang Z,Hou X,Pan S,Poeppelmeier K R 2017 J.Am.Chem.Soc.139 10645
[64]Wang Y,Zhang B,Yang Z,Pan S 2018 Angew.Chem.Int.Ed.57 2150
[65]Luo M,Liang F,Song Y,Zhao D,Xu F,Ye N,Lin Z 2018 J.Am.Chem.Soc.140 3884
[66]Petrov V 2015 Prog.Quantum Electron.42 1
[67]Wu K,Yang Z,Pan S 2016 Angew.Chem.Int.Ed.55 6712
[68]Wu K,Zhang B,Yang Z,Pan S 2017 J.Am.Chem.Soc.139 14885
[69]Liang F,Kang L,Lin Z,Wu Y 2017 Cryst.Growth Des.17 2254
[70]Li C,Yin W L,Gong P F,Li X S,Zhou M L,Mar A,Lin Z S,Yao J Y,Wu Y C,Chen C T 2016 J.Am.Chem.Soc.138 6135
[71]Halasyamani P S,Poeppelmeier K R 1998 Chem.Mater.10 2753
[72]Banerjee S,Malliakas C D,Jang J I,Ketterson J B,Kanatzidis M G 2008 J.Am.Chem.Soc.130 12270
[73]Bera T K,Song J H,Freeman A J,Jang J I,Ketterson J B,Kanatzidis M G 2008 Angew.Chem.Int.Ed.47 7828
[74]Bera T K,Jang J I,Song J H,Malliakas C D,Freeman A J,Ketterson J B,Kanatzidis M G 2010 J.Am.Chem.Soc.132 3484
[75]Hanna D C,Rutt H N,Stanley C R,Smith R C,Lutherda B 1972 IEEE J.Quantum Electron.8 317
[76]Li G,Wu K,Liu Q,Yang Z,Pan S 2016 J.Am.Chem.Soc.138 7422
[77]Liu B W,Zeng H Y,Jiang X M,Wang G E,Li S F,Xu L,Guo G C 2016 Chem.Sci.7 6273
[78]Lekse J W,Moreau M A,McNerny K L,Yeon J,Halasyamani P S,Aitken J A 2009 Inorg.Chem.48 7516
[79]Liang F,Kang L,Lin Z,Wu Y,Chen C 2017 Coord.Chem.Rev.333 57
[80]ParthéE 1964 Crystal Chemistry of Tetrahedral Structures(1st Ed.)(New York:Gordon and Breach Science Publishers Inc)pp1–25
[81]Wu K,Yang Z,Pan S 2017 Chem.Commun.53 3010
[82]Wu K,Pan S 2017 Crystals 7 107
[83]Li G,Chu Y,Zhou Z 2018 Chem.Mater.30 602
[84]Jantz W,Koidl P,Wettling W 1983 Appl.Phys.AMater.Sci.Pro.30 109
[85]Zhang M J,Jiang X M,Zhou L J,Guo G C 2013 J.Mater.Chem.C 1 4754
[86]Zhang G,Li Y,Jiang K,Zeng H,Liu T,Chen X,Qin J,Lin Z,Fu P,Wu Y,Chen C 2012 J.Am.Chem.Soc.134 14818
[87]Wu Q,Meng X,Zhong C,Chen X,Qin J 2014 J.Am.Chem.Soc.136 5683
[88]Zhang X,Jiang X,Li Y,Lin Z,Zhang G,Wu Y 2015 CrystEngComm 17 1050
[89]Kwon O P,Kwon S J,Jazbinsek M,Brunner F D J,Seo J I,Hunziker C,Schneider A,Yun H,Lee Y S,Guenter P 2008 Adv.Funct.Mater.18 3242
[90]Kalmutzki M,Strobele M,Wackenhut F,Meixner A J,Meyer H J 2014 Inorg.Chem.53 12540
[91]Divya R,Nair L P,Bijini B R,Nair C M K,Gopakumar N,Babu K R 2017 Physica B 526 37
[92]Xia M,Zhou M,Liang F,Meng X,Yao J,Lin Z,Li R 2018 Inorg.Chem.57 32
[93]Song Y,Luo M,Liang F,Ye N,Lin Z 2018 Chem.Commun.54 1445
[94]Liu J W,Wang P,Chen L 2011 Inorg.Chem.50 5706
[95]Xia M,Jiang X,Lin Z,Li R 2016 J.Am.Chem.Soc.138 14190
[96]Majchrowski A,Chrunik M,Rudysh M,Piasecki M,Ozga K,Lakshminarayana G,Kityk I V 2017 J.Mater.Sci.53 1217
[97]Daub M,Krummer M,Hoff mann A,Bayarjargal L,Hillebrecht H 2017 Chem.Eur.J.23 1331
[98]Zhao S,Yang Y,Shen Y,Zhao B,Li L,Ji C,Wu Z,Yuan D,Lin Z,Hong M,Luo J 2017 Angew.Chem.Int.Ed.56 540
[99]Peng G,Yang Y,Tang Y H,Luo M,Yan T,Zhou Y,Lin C,Lin Z,Ye N 2017 Chem.Commun.53 9398
[100]Song Y,Luo M,Liang F,Lin C,Ye N,Yan G,Lin Z 2017 Dalton Trans.46 15228
[101]Jain A,Ong S P,Hautier G,Chen W,Richards W D,Dacek S,Cholia S,Gunter D,Skinner D,Ceder G,Persson K A 2013 APL Mater.1 011002
[102]Kumar N,Najmaei S,Cui Q N,Ceballos F,Ajayan P M,Lou J,Zhao H 2013 Phys.Rev.B 87 161403
[103]Li Y,Rao Y,Mak K F,You Y,Wang S,Dean C R,Heinz T F 2013 Nano Lett.13 3329
[104]Zhou X,Cheng J X,Zhou Y B,Cao T,Hong H,Liao Z M,Wu S W,Peng H L,Liu K H,Yu D P 2015 J.Am.Chem.Soc.137 7994
[105]Wu L,Patankar S,Morimoto T,Nair N L,Thewalt E,Little A,Analytis J G,Moore J E,Orenstein J 2016 Nat.Phys.13 350
[106]Mikhailov S A 2011 Phys.Rev.B 84 045432
