Bi x Ba1−x TiO 3电子及能∗带结构的第一性原理研究

房玉真 孔祥晋 王东亭 崔守鑫 刘军海†

1 引 言

目前,光催化技术是一种全新的“绿色技术”[1].其中研究较深入的TiO2系列光催化尚存在一些关键科学技术难题,如二氧化钛的禁带宽度(Eg=3.2 eV)过宽,太阳能利用率低[2]等.近几年的研究发现,钙钛矿结构的光催化剂具有合适的禁带宽度和良好的化学稳定性,对可见光反应响应良好.报道较多的如铁酸铋(Eg=2.2—2.8 eV)[3]、钛酸铋(Eg=2.6—2.8 eV)[4],正在尝试着用于光催化分解水制氢、降解有机染料、光降解有机污染物等重要光催化过程[5,6].

在AB O3钙钛矿复合氧化物结构中,A位的稀土元素一般无催化活性,大多数只是作为晶体稳定点阵的组成部分.B位元素可作为活性位起催化作用,研究发现单独B位元素的氧化物与AB O3的活性几乎处于同一级别[7],但是若对A位或B位上的金属离子部分取代,它仍然可以保持原来的钙钛矿结构不变,但会形成阳离子的反常价态,并形成点缺陷或氧空位影响钙钛矿复合氧化物的电子结构及传递性质,从而影响其催化活性.

BaTiO3是一种典型具有铁电性的钙钛矿复合氧化物,除铁电性之外,还具有良好的高介电常数和大的电光系数[8],经特定的元素改性之后,还具有较好的光催化降解活性[9],如可降解并矿化包括甲基红、甲基橙和亚甲基蓝在内的多种有机染料[10−12].但是,纯的BaTiO3钙钛矿复合氧化物带隙较宽,仅能被紫外光所激发.同时,在向表面迁移的过程中光生电荷较容易复合,这些不足降低了BaTiO3的光催化效果,并限制了BaTiO3光催化剂的应用.而钙钛矿结构的铋基3d过渡金属氧化物具有丰富的磁学、电学和光学性质[13,14],研究也表明铋基钙钛矿结构具有合适的禁带宽度和良好的化学稳定性,对可见光反应响应良好[15,16].Bi—Ti—O结合除了可形成Bi4Ti3O12,Bi2Ti2O7,Bi2Ti4O11,Bi12TiO20[17−19]等多种晶相结构的氧化物外,在一定的条件下,也可形成BiTiO3结构[20].因此基于TiO2优异的光催化性能和钙钛矿独特可剪裁且本身禁带较窄的结构特点,期望通过Bi掺杂实现对钙钛矿BaTiO3能隙的调控,Bi取代后会影响BaTiO3的导带和价带,并可能会引起晶格中的点缺陷和氧空位.点缺陷的存在会形成局域能级,将有利于电子-空穴对的产生;氧空位可以成为光生电子的陷阱,延长其寿命,减小电子-空穴的复合率,从而可能有效改善BaTiO3对有机污染物的降解活性.

密度泛函理论的第一性原理计算是模拟多体系统电子结构的有效方法[21−23].关于钙钛矿材料的电子能带结构及光学吸收性质,除了通过实验直接测定外,还可以采用理论计算的方法进行较为精确的计算.随着有机无机杂化钙钛矿(如MAPbI3)成为光伏运用的新型活性材料,寻找新型环境友好的无铅钙钛矿结构光伏材料成为了研究热点.Zhao等[24−27]采用第一性原理计算了Ge基、Sn基无铅钙钛矿的电子结构以及光学吸收性能和载流子迁移率等性质,预测它们将是有前途的光伏材料.

本文基于赝势平面波的方法,选取B位含Ti的BaTiO3为研究对象,通过Bi元素对钛酸钡A位上的Ba部分取代,对取代后的BixBa1−xTiO3复合氧化物电子及能带结构进行第一原理性分析.考察不同Bi取代量对BaTiO3钙钛矿催化剂的能带调控规律以及对其电子结构和光学性质的影响,这将有助于预测该材料在光催化领域的性能特点及应用领域.

2 计算方法及模型

2.1 计算方法

采用基于第一性原理的赝势平面波方法进行计算,由Material Studio软件中的CASTEP模块完成[28,29]. 选取广义梯度近似(GGA)中的Perdew-Wang(PW91)作为交换关联势,采用Broyden-Fletcher-Goldfarb-Shanno[30]算法对BixBa1−xTiO3(x=0,0.125,0.250,0.375,0.500,0.625,0.750,0.875)8种晶体结构模型进行优化.利用周期性边界条件,采用超软赝势描述芯电子与价电子之间的相互作用,其中平面波的截断能Ecut取为340 eV.选取O的2s22p4,Ti的3s23p63d24s2,Ba的5s25p66s2,Bi的6s26p3组态电子作为价电子,其余轨道电子为芯电子进行计算.在布里渊区采用Monkhorst-Pack方法选取3×3×3的K点网格,保证体系能量在平面波基底水平上的收敛.在优化BixBa1−xTiO3结构和计算总能时,电子结构自洽精度设为每个原子能量收敛至1×10−5eV,原子间最大相互作用力为0.03 eV/Å,最大应力为0.05 GPa,原子最大位移为0.001Å.

2.2 理论模型

钙钛矿复合氧化物的命名来源于一种稀有的CaTiO3矿,其化学组成通常可以用AB O3形式来表达,本文基于具有Pm3m立方对称性的典型钙钛矿复合氧化物为结构模型,A位离子为Ba2+或Bi3+,分居立方体的8个角上,B位为Ti3+,占据晶胞的中心,氧则位于立方体6个面的面心处.其中A位离子有12个氧配位,这些氧离子同时又属于8个BO6八面体共享角.其结构模型可用分子式BixBa1−xTiO3形式来表达,如图1所示,图1(a)为BaTiO3的理论模型,图1(b)为x=0.125的Bi0.125Ba0.875TiO3理论模型.

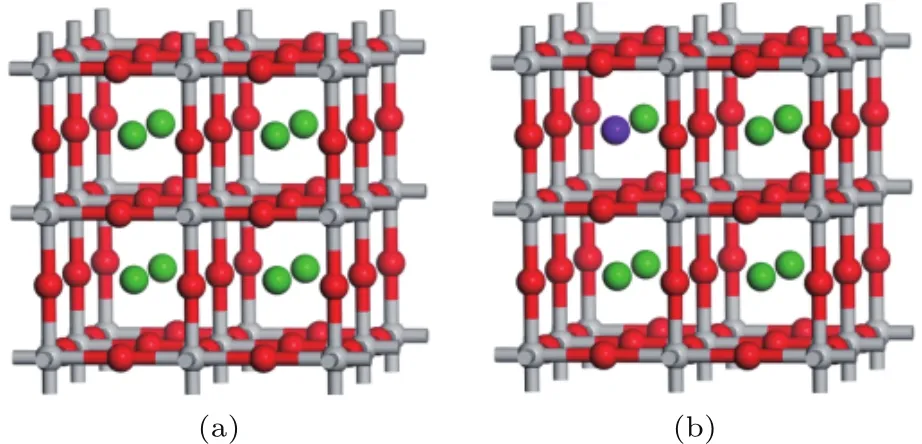
图1 理论模型 (a)BaTiO3;(b)Bi0.125Ba0.875TiO3(绿色代表Ba原子,红色代表O原子,灰色代表Ti原子,紫色代表Bi原子)Fig.1.Theoretical models:(a)BaTiO 3;(b)Bi0.125-Ba0.875TiO 3(green represent Ba atoms,red represent O atoms,gray represent Ti atoms,and purple represent Bi atoms).

3 结果与讨论

3.1 结合能

结合能是用来表征原子之间的结合力强度和相对稳定性的重要基础参数.通过CASTEP模块对BixBa1−xTiO3(x=0,0.125,0.250,0.375,0.50,0.625,0.750,0.875)进行结构优化,计算得到稳定构型的晶胞参数及总能量,各构型的晶格常数,总能及结合能列于表1.通过(1)式计算获得各构型的结合能[31,32]:

其中∆E BixBa1−xTiO3为Bi x Ba1−x TiO3的结合能;

EBi,EBa,ETi和EO分别为自由的Bi原子,Ba原子,Ti原子和O原子总能;EBixBa1xTiO3为分子BixBa1−xTiO3的总能.根据(1)式求出8种结构模型的结合能,BaTiO3构型结合能较大,说明钙钛矿结构的钛酸钡较其他结构稳定,Bi取代后会导致构型能量升高.

表1 Bi x Ba1−x TiO 3的晶胞参数、总能及结合能Table 1.Crystal lattice parameters,total energy and binding energy of Bi x Ba1−x TiO 3.

3.2 晶体结构

钙钛矿结构的形成会受到很多因素的限制,其中最重要的就是要满足容积因子t的要求,如(2)式所示:

其中t为容积因子;RA为钙钛矿A位原子的离子半径;RB为钙钛矿B位原子的离子半径;RO为钙钛矿中O原子的离子半径.

Bi取代之后,BixBa1−xTiO3构型仍保持钙钛矿结构,但是随着取代量的增加会出现新的杂质物相.通过查阅O,Ba,Bi,Ti的离子半径,按照(2)式计算发现BixBa1−xTiO3复合氧化物可形成钙钛矿结构.将优化后的构型利用Refl ex模块计算得到了各构型的X射线衍射(XRD)谱图.如图2所示,不同取代量的物质的XRD图上均有钙钛矿结构的特征衍射峰(2θ=22.15◦,31.55◦,38.85◦,45.2◦,50.9◦,56.15◦,65.8◦,70.4◦,75.05◦,79.15◦),这说明各构型均属于典型的钙钛矿结构.值得指出的是,当Bi的取代量增加后,可能会形成大量点缺陷或氧空位导致形成非整比化合物.随着Bi取代量的增加,XRD图谱上出现了一些杂峰(2θ=11.05◦,24.8◦,33.5◦,46.65◦,57.4◦,62.3◦,76.1◦),通过对照PDF卡片,发现这些杂峰可能来源于产生的新物相BaBi4Ti4O15(PDF-#73-2184),当Bi的取代量x=0.5时,新物相BaBi4Ti4O15的特征衍射峰最明显.

图2 Bi x Ba1−x TiO3的X射线粉末衍射图Fig.2.X-ray powder diff raction pattern of Bi x Ba1−x TiO3.

Bi取代之后BixBa1−xTiO3钙钛矿复合氧化物的对称性下降.由于Bi与Ba的离子半径不同,且在钙钛矿型复合氧化物中的价态有区别.因此Bi离子取代Ba之后,具有高对称性的晶胞内离子会在平衡位置发生微小的位移,从而也会使晶胞参数发生一定的变化,如表1所列.由于Bi3+离子半径(0.130 nm)小于Ba2+离子半径(0.175 nm),当Bi取代部分Ba之后会使BixBa1−xTiO3晶胞体积减小(x=0.5除外,可能主要是由于新物相的产生引起的),Bi—O或Ba—O键发生变化;在取代后的BixBa1−xTiO3构型中,八面体TiO6的Ti不在中心位置,由计算结果可知,当Bi的取代量x=0.125,0.25时,钙钛矿复合氧化物将从立方原始格子降为四方原始格子,空间群Pm3m转换为P4mm,随着Bi的取代量增加,对称性进一步降低为Pmm2(C2V-1)(x=0.375)和Pm(CS-1)(x=0.5,0.625,0.75);当取代量x=0.875时,对称性又变为Pmm2(C2V-1).Bi和Ba离子半径及价态的不同导致取代后的BixBa1−xTiO3晶体对称性降低,杂质物相的生成及结合能减小.

3.3 能带结构

在对钙钛矿结构的BixBa1−xTiO3能带结构的计算中,发现布里渊区高对称点方向的能带结构,价带顶和导带底都位于G点处,说明BixBa1−xTiO3为直接带隙型半导体.Bi的取代量从0到0.875,对应的禁带宽度分别为1.7605,1.9611,2.1432,2.3717,2.5935,2.6928,2.4782,1.2463 eV,具体结果见表2.即A位离子为Bi和Ba共同占据时其禁带宽度较宽,x=0.625时,达到最大值2.6928 eV.随着掺杂量的继续增加,带隙又迅速降低.

有效质量是衡量光催化活性的一个重要物理量,根据半导体能带理论,空穴或电子的有效质量取决于它们所处状态下的能带结构E-k关系,由不同价带E-k关系中能量E的二阶微分表征,即按照(3)式计算可得到空穴和电子的有效质量:

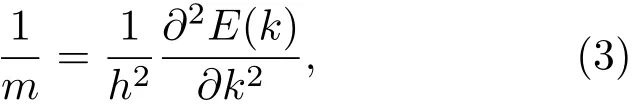
其中m为空穴或电子的有效质量;h为普朗克常数.载流子的浓度是一个与温度、禁带宽度和有效质量相关的函数,可表示为

其中ni为载流子的浓度;m∗n为电子有效质量;m∗p为空穴有效质量;m0为电子质量;T为热力学温度;Eg为禁带宽度.

为了计算有效质量,建立了价带E(k)-k关系模型. 结合计算所得的能带结构图,对高对称点G附近的价带顶和导带底的能带曲线求二阶导数来获得空穴和电子的有效质量m∗p和m∗n,各空穴和电子的有效质量均以电子质量m0为基准. 当x从0到0.875,对应的空穴有效质量m∗p分别为:3.9386m0,2.7745m0,2.7652m0, 2.4210m0, 3.0975m0, 1.4471m0,1.8092m0和3.1064m0; 电子有效质量m∗n分别为:1.4255m0,1.4198m0,1.3272m0,1.2029m0,1.2467m0,1.4212m0,1.2819m0和1.9006m0. 掺杂Bi后Bi0.875Ba0.125TiO3的空穴及电子有效质量均增加,这是由于其带隙最小引起的. 而Bi0.5Ba0.5TiO3的空穴有效质量也增加,可能是由于BaBi4Ti4O15新物相的形成改变了价带顶和导带底结构的原因.其他构型中由于Bi元素的掺杂均会引起空穴和电子有效质量的变小.

当温度为300 K时,将计算得到的禁带宽度Eg,m∗P,m∗n结果代入(4)式就可以得到该温度下的载流子浓度.当x从0到0.875,载流子的浓度ni分别为1.00×1020,8.19×1019,7.67×1019,6.35×1019,6.10×1019,5.20×1019,5.73×1019和1.13×1020cm−3.计算发现改变能带的结构,使带隙变宽可以使载流子浓度减小,带隙变窄能使载流子浓度增加.

图3 Bi x Ba1−x TiO 3沿高对称点的电子能带结构图 (a)x=0;(b)x=0.125;(c)x=0.250;(d)x=0.375;(e)x=0.500;(f)x=0.625;(g)x=0.750;(h)x=0.875Fig.3.Electron band structure along a high symmetry point of Bi x Ba1−x TiO3:(a)x=0;(b)x=0.125;(c)x=0.250;(d)x=0.375;(e)x=0.500;(f)x=0.625;(g)x=0.750;(h)x=0.875.

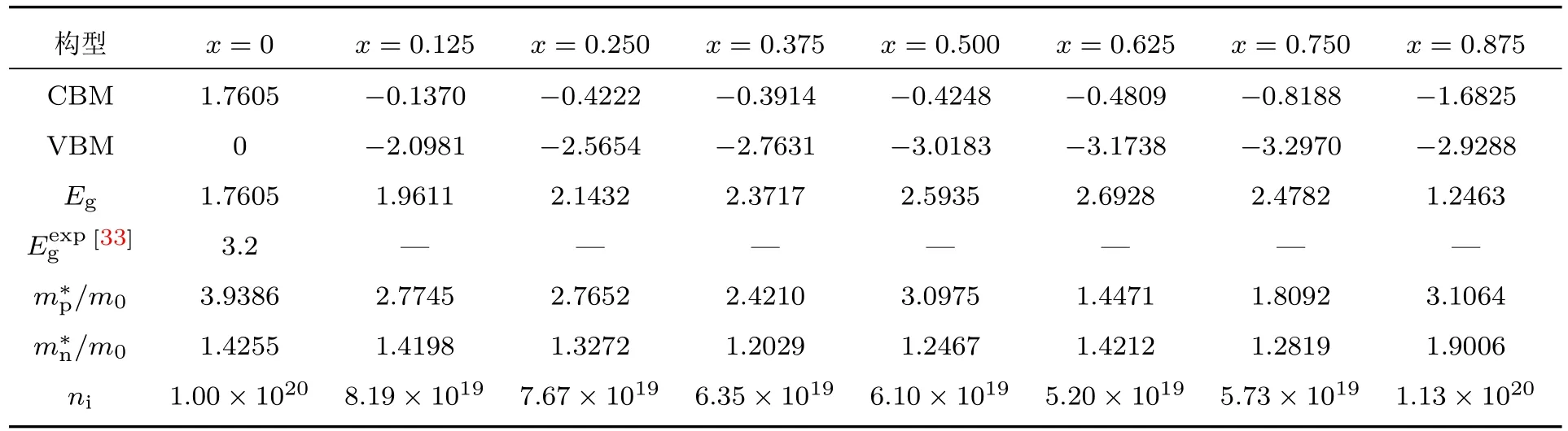
表2 Bi x Ba1−x TiO 3在价带顶(VBM)、导带底(CBM)的特征能量(eV)和禁带宽度E g(eV),高对称G点附近的空穴及电子的有效质量(m∗p,m∗n)以及温度为300 K时的载流子浓度n i(cm−3)Table 2.Characteristic energy(eV)at the top of the valence band(VBM)and the bottom of the conduction band(CBM),their band width E g(eV),eff ective mass of holes(m∗p)and electrons(m∗n),and the carrier concentration n i(cm−3)nearby the high symmetry G point of Bi x Ba1−x TiO3.

图3为BixBa1−xTiO3沿高对称点的电子能带结构图.结合表2和图3,可看出计算所得的带隙较实验值偏小,出现这种现象是由于采用的计算方法所导致的,在计算过程中采用GGA会导致理论基本带隙宽度比实验值小30%—50%[34].不过其作为一种有效的近似方法,理论模拟计算得到的结果的相对值还是很准确的,不影响对能带结构和电子结构规律的观察[35].对比图3(a)和图3(b)—图3(h),可看出Bi的取代使钙钛矿复合氧化物产生了很多新的表面态,主要体现在新的杂质能级的形成.由于铋原子显+3价,钡显+2价,当作为施主的Bi原子取代钙钛矿晶格中的Ba原子后,为了维持钙钛矿复合氧化物的电中性,会形成一定的缺陷或氧空位[36,37],导致了杂质能级的形成.另外,Bi3+离子与Ba2+离子相比,它除了满足共价键配位以外,还可提供一个多余的电子,这就导致了半导体中导带电子浓度的增加,载流子增多,那么掺杂费米能级随即进入导带.随着取代量的增加,掺杂费米能级上移越显著,所产生的杂质能级越多,且导带底和价带顶均明显下移.Bi取代后引起的载流子增多,将改善BixBa1−xTiO3催化剂的光催化性能.

3.4 电子态密度

图4为BixBa1−xTiO3的电子态密度图,它反映了各电子态对导带和价带的贡献.在BaTiO3构型中,价带主要是O-2p态的贡献,导带主要有Ti-3d态贡献,费米能级位于价带边,为p型半导体.当用Bi取代Ba之后,如在Bi0.125Ba0.725TiO3结构中,掺杂费米能级位于导带边,为n型半导体.随着Bi掺杂量的增加,发现费米能级就越深入导带区间,Bi为施主杂质.Bi取代量越高,导带中就有更多的电子(多数为载流子),其半金属化合物的特点就越来越强.在Bi取代的构型中,态密度值较BaTiO3高很多.对比能带结构图,这主要是由于Bi取代后导致原钙钛矿晶格产生缺陷或氧空位从而引入了很多新的杂质能级,其价带区间的态密度除了由O-2p的贡献外,还有较大部分来自于Bi-6p,导带区间的态密度主要由Ti-3d态决定,也有少量Bi-6p和O-2p态电子的贡献.

由图4(a)可知x=0时费米能级在价带附近,电子的态密度几乎完全来自于Ti-3d和O-2p电子的贡献,表明Ti-3d和O-2p轨道发生强烈的轨道杂化,Ti原子和O原子之间存在强烈的共价作用,导带主要由Ti-3d和Ba-5p轨道构成.因此,Ba-TiO3的电子输运性质及载流子类型主要由Ti-3d态、O-2p态和Ba-5p态电子决定.

由图4(b)—图4(h)可知,在x>0.125的构型中,掺杂费米能级上移至导带附近,电子的态密度大部分来自Bi-5d,Bi-6s,Bi-6p态电子的贡献,而价带除了来自于Ti-3d和O-2p外,还有一部分来自于Bi-6s.因此,BixBa1−xTiO3的电子输运性质及载流子类型主要由Ti-3d,O-2p,Bi-6s和Bi-6p电子态电子决定.

3.5 光学性质

采用优化后的构型对BixBa1−xTiO3进行了光学性质的计算,获得了如图5所示的吸收光谱.从图5(a)和图5(b)可看出,BaTiO3的吸收带峰大约在290 nm附近,随着Bi取代量的增加,吸收边发生轻微的蓝移.当x=0.5时,吸收边蓝移至200 nm附近.Bi的取代量继续增加,主吸收峰继而又逐渐红移,当x=0.875时,吸收峰红移至230 nm处.掺杂后的体系与BaTiO3相比,峰强度增加,将有助于紫外光的吸收,提高紫外光的光催化效果.值得注意的是,当Bi的取代量x=0.375,0.625,0.750,0.875时,在600—800 nm范围内出现较宽的吸收峰,说明该体系将对可见光有一定的吸收能力.

图4 Bi x Ba1−x TiO3的电子分态密度(PDOS)图 (a)x=0;(b)x=0.125;(c)x=0.250;(d)x=0.375;(e)x=0.500;(f)x=0.625;(g)x=0.750;(h)x=0.875Fig.4.Partial density of electronic states(PDOS)of Bi x Ba1−x TiO3:(a)x=0;(b)x=0.125;(c)x=0.250;(d)x=0.375;(e)x=0.500;(f)x=0.625;(g)x=0.750;(h)x=0.875.

图5 Bi x Ba1−x TiO 3的光吸收谱 (a)x=0,0.125,0.250,0.375;(b)x=0.500,0.625,0.750,0.875Fig.5.Optical absorption spectra of Bi x Ba1−x TiO 3:(a)x=0,0.125,0.250,0.375;(b)x=0.500,0.625,0.750,0.875.

4 结 论

采用基于密度泛函理论的第一性原理赝势平面波的方法,对BixBa1−xTiO3晶体结构进行优化.计算了结合能、能带结构、电子态密度等性质.对计算结果进行讨论分析,主要得到以下结论.

1)在分子BixBa1−xTiO3中,当x=0时,构型结合能较大,说明未取代的BaTiO3钙钛矿结构较其他组成结构稳定,Bi的取代会导致钙钛矿结构对称性下降,当x=0.500时,体相中除了钙钛矿结构外,将会有BaBi4Ti4O15新物相生成.

2)计算所得BaTiO3的带隙宽度为1.7605 eV;当Bi取代钛酸钡A位离子Ba时,可调节BixBa1−xTiO3的禁带宽度.从x=0.125到x=0.625时,Bi的取代量越大,其带隙越宽,当x=0.625时,禁带宽度到达最大(2.6928 eV).x>0.625时,禁带宽度又逐渐减小,当x=0.875时,其禁带宽度达到最小(1.2463 eV),比BaTiO3的带隙宽度还低0.5142 eV,预测Bi基钙钛矿的能带宽度将低于Ba基钙钛矿.

3)BixBa1−xTiO3是一种直接带隙半导体,由态密度图可看出,其价带顶主要是O-2p与Bi-6s态杂化而成,导带底主要由Ti-3d态构成.因此,BaTiO3的电子输运性质及载流子类型主要由Ti-3d态和O-2p态电子决定. Bi取代后,BixBa1−xTiO3的电子输运性质及载流子类型主要由Ti-3d,O-2p,Bi-6s,Bi-6p电子态电子决定,且态密度值显著增加.

[1]Serpone N,Emeline A V 2012 J.Phys.Chem.Lett.3 673

[2]Kazuya N,Akira F 2012 J.Photoch.Photobi.C:Photoch.Rev.13 169

[3]Zhu X H,Hang Q M,Xing Z M,Yang Y,Zhu J M,Liu Z G,Ming N B,Zhou P,Song Y,Li Z S,Yu T,Zou Z G 2011 J.Am.Ceram.Soc.94 2688

[4]Hou J G,Jiao SQ,Zhu H M 2011 J.Solid.State.Chem.184 154

[5]Tayyebeh S,Byeong-Kyu L 2016 J.Hazard.Mater.316 122

[6]Tong T,Zhang H,Chen J G,Jin D R,Cheng J R 2016 Catal.Commun.87 23

[7]Peña M A,Fierro J L G 2001 Chem.Rev.101 1981

[8]Sitko D,Bak W,Garbarz-Glos B,Budziak A,Kajtoch C Kalvane A 2013 Mat.Sci.Eng.49 012050

[9]Xian T,Di L J,Ma J,Sang C C,Wei X G,Zhou Y J 2017 Chin.J.Mater.Res.31 102(in Chinese)[县涛,邸丽景,马俊,桑萃萃,魏学刚,周永杰2017材料研究学报31 102]

[10]Wang P G,Fan C M,Wang Y W,Ding G Y,Yuan P H 2013 Mater.Res.Bull.48 869

[11]Devi L G,Krishnamurthy G 2011 J.Phys.Chem.A 115 460

[12]Cui Y F,Briscoe J,Dunn S 2013 J.Chem.Mater.25 4215

[13]Sarveswaran G,Subramanian B,Mohan S 2014 J.Mater.Chem.C 2 6835

[14]He C,Ma Z J,Sun B Z,Sa R J,Wu K C 2015 J.Alloys Compd.623 393

[15]Li Z X,Shen Y,Guan Y H,Hu Y H,Lin Y H,Nan C W 2014 J.Mater.Chem.A 2 1967

[16]Klara R,Roberto K,Mònica R,Hans H R,Frank-Dieter K,Anett G 2014 Chem.Eng.J.239 322

[17]Xu X H,Yao W F,Zhang Y,Zhou A Q,Hou Y,Wang M 2005 Acta Chim.Sin.63 5(in Chinese)[许效红, 姚伟峰,张寅,周爱秋,侯云,王民2005化学学报63 5]

[18]Wei W,Dai Y,Huang B B 2009 J.Phys.Chem.C 113 5658

[19]Murugesan SK,Muhammad N H,Yanfa Y,Mowafak M J,Vaidyanathan S 2010 J.Phys.Chem.C 114 10598

[20]Baedi F,Mircholi H 2015 Optik 126 1505

[21]Cao D,Liu B,Yu H L,Hu W Y,Cai M Q 2015 Eur.Phys.J.B 88 75

[22]Liu B,Wu L J,Zhao Y Q,Wang L Z,Cai M Q 2016 J.Magn.Magn.Mater.420 218

[23]Cao D,Liu B,Yu H L,Hu W Y,Cai M Q 2013 Eur.Phys.J.B 86 504

[24]Zhao Y Q,Liu B,Yu Z L,Ma J M,Wan Q,He P B,Cai M Q 2017 J.Mater.Chem.C 5 5356

[25]Zhao Y Q,Liu B,Yu Z L,Cao D,Cai M Q 2017 Electrochim.Acta 247 891

[26]Zhao Y Q,Wang X,Liu B,Yu Z L,Yu H L 2018 Org.Electron.53 50

[27]Wu L J,Zhao Y Q,Chen C W,Wang L Z,Liu B,Cai M Q 2016 Chin.Phys.B 25 107202

[28]Milman V,Refson K,Clark S J,Pickard C J,Yates J R,Gao SP,Hasnip P J,Probert M I J,Perlov A,Segall M D 2010 J.Mol.Struct.:Theochem.954 22

[29]Luo Z F,Cen W F,Fan M H,Tang J J,Zhao Y J 2015 Acta Phys.Sin.64 147102(in Chinese)[骆最芬,岑伟富,范梦慧,汤家俊,赵宇军2015物理学报64 147102]

[30]Vanderbilt D 1990 Phys.Rev.B 41 7892

[31]Zhao L K,Zhao E J,Wu Z J 2013 Acta Phys.Sin.62 046201(in Chinese)[赵立凯,赵二俊,武志坚2013物理学报62 046201]

[32]Ma L,Yin Y P,Ding X B,Dong C Z 2017 Acta Phys.Sin.66 063101(in Chinese)[马磊,殷耀鹏,丁晓彬,董晨钟2017物理学报66 063101]

[33]Suzuki K,Kijima K 2005 Jpn.J.Appl.Phys.44 2081

[34]Robertson J,Xiong K,Clark S J 2006 Phys.Status Solidi 243 2054

[35]Zhao Z Y,Liu Q J,Zhang J,Zhu Z Q 2007 Acta Phys.Sin.56 6592(in Chinese)[赵宗彦,柳清菊,张瑾,朱忠其2007物理学报56 6592]

[36]Zhao Y Q,Wu L J,Liu B,Wang L Z,Cai M Q 2016 J.Power Sources 313 96

[37]Ren C,Li X Y,Luo Q W,Liu R P,Yang Z,Xu L C 2017 Acta Phys.Sin.66 157101(in Chinese)[任超,李秀燕,落全伟,刘瑞萍,杨致,徐利春2017物理学报66 157101]