激发光线宽对原子光致漂移速率的影响∗

杨佳琦 刘加东 刘涛† 张志忠

1 引 言

光致漂移现象是存在于光场中的一种气体动力学效应,其原理是:基于多普勒效应,利用激光对某种气体粒子进行“速度选择性激发”,使得在激光传播方向上具有特定速度分量的该种气体粒子有一部分布居到激发态上,而具有其他速度分量的粒子保持基态不变.该种气体粒子处于缓冲气体的环境中,由于两种能态上的粒子与缓冲气体的碰撞输运特性有差异,使得气体粒子在选择的速度方向上产生宏观的定向移动[1,2].光致漂移现象在天体物理[3−6]、半导体物理[7]和同位素分离[8−12]等领域均具有广泛的应用.

光致漂移速率是表征光致漂移效应的一个关键参数,定义为分布在各个能级上的吸收气体粒子沿激光传播方向投影速度分量的平均值[13].光致漂移现象一经发现,研究者们便围绕漂移速率的理论研究开展了大量的工作,其中大多数理论工作把碱金属原子作为研究对象[13−21].对于光致漂移而言,激发光线宽会影响原子激发的速度选择性,进而影响漂移速率的大小,因此是光致漂移研究中不可忽视的一个影响因素.在国外已有的理论研究中,通常把激发光作为单色光进行处理,很少考虑激发光线宽对漂移速率的影响[13−19].1981年,Popov等[20]首次发表与激发光线宽相关的理论研究,但该研究是采用二能级原子模型对原子光致漂移过程进行描述,没有考虑能级简并与超精细能级对光致漂移的影响.柴俊杰等[21]的研究中对线宽因素的影响稍有涉及,但针对碰撞问题采用的是碰撞弛豫时间近似的数学处理方法,这种方法非常粗略,只适合对漂移速率问题做一些简单的定性分析.

本文在理论建模时,统一考虑能级简并、超精细结构以及碰撞模型等各个因素,以文献[13]中碱金属原子光致漂移速率方程理论为基础,引入能级简并与超精细能级的影响,利用强碰撞模型描述原子与缓冲气体的碰撞作用,建立四能级速率方程模型描述光致漂移过程中原子的能级跃迁.并运用数值方法对速率方程进行计算,根据计算结果分析了激发光线宽对碱金属原子漂移速率的影响.

2 原子光致漂移速率方程理论

通常碱金属原子的光谱结构较为简单,基于碱金属原子基态超精细分裂宽度与多普勒展宽基本在一个量级,所以计算时要考虑基态超精细结构能级的影响.而激发态的超精细分裂宽度远小于激发态精细结构的能级差以及原子的多普勒展宽,故在建立速率方程时可以忽略激发态的超精细结构.基于上述原因,在建立理论模型时主要围绕图1所示的4个能级之间原子跃迁进行讨论.其中能级1和2代表原子基态的超精细能级结构,能级3和4代表原子激发态的精细结构.Aij(i=3,4;j=1,2)为自发辐射速率,hij为速度选择性激发的速率,ζij为碰撞作用因子.

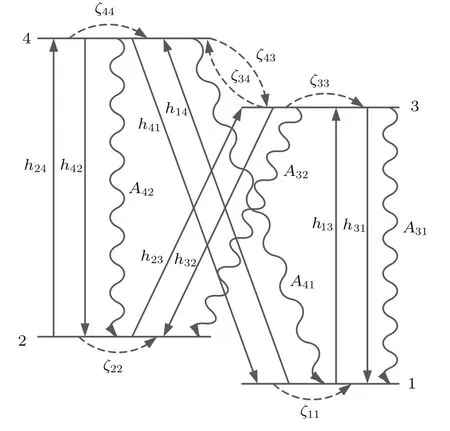
图1 原子的简化能级结构Fig.1.Simplifi ed energy level structure of atoms.

在光致漂移过程中,碱金属原子除了经历基态原子的激发、激发态原子的自发辐射和受激辐射等过程,还会与其他原子产生碰撞.由于碱金属原子密度远小于缓冲气体密度,此处忽略碱金属原子之间的碰撞,仅考虑碱金属原子同缓冲气体之间的碰撞.碱金属原子与缓冲气体之间的碰撞过程会造成速度的改变和能级的跃迁,主要包括:1)碰撞前后能级不变,仅速度发生改变;2)激发态精细结构能级上的原子由于碰撞引起的无辐射跃迁.由于基态超精细结构能级之间的碰撞跃迁截面较小,此处忽略其碰撞跃迁过程.

综合上述分析并结合图1,可以得到光致漂移过程中碱金属原子各能级粒子数布居的速率方程如下[13]:

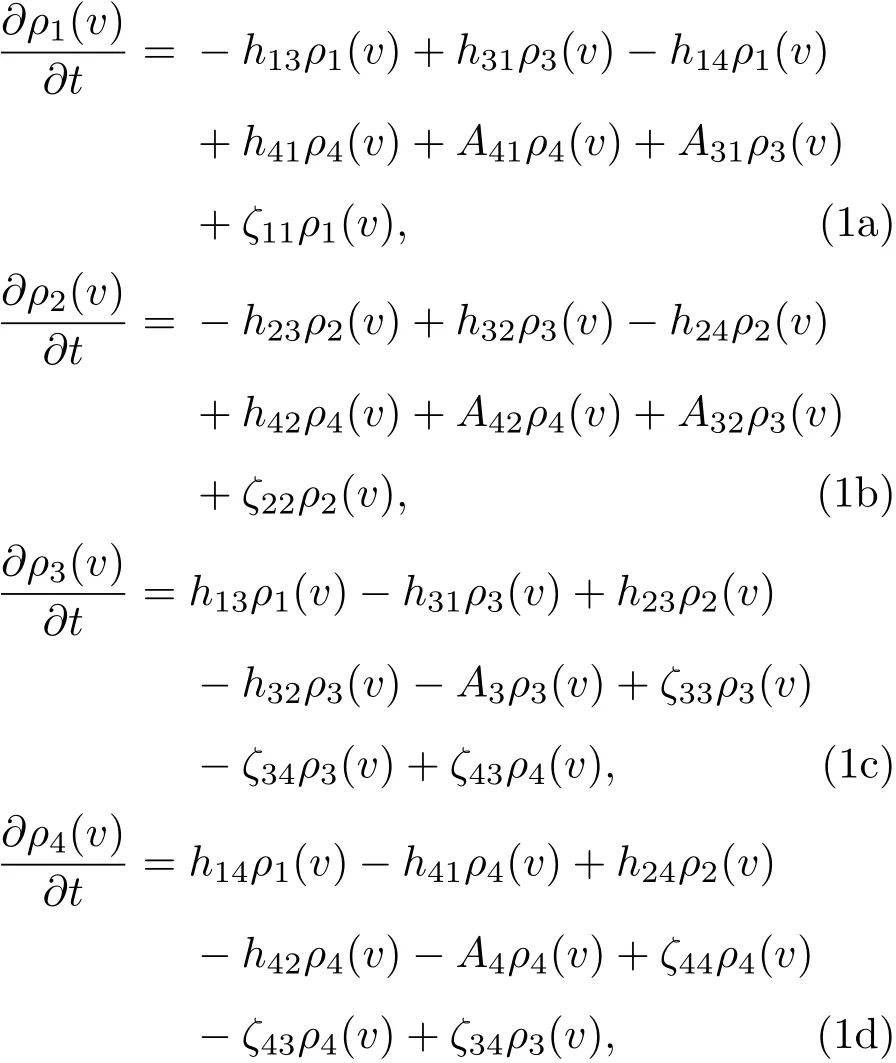
式中ρi(v)(i=1,2,3,4)为能级i上原子的速度分布函数(其中v指激光传播方向上的粒子速度);t为时间;Ai=Ai1+Ai2(i=3,4);速度选择性激发的速率hij表达式为[13]

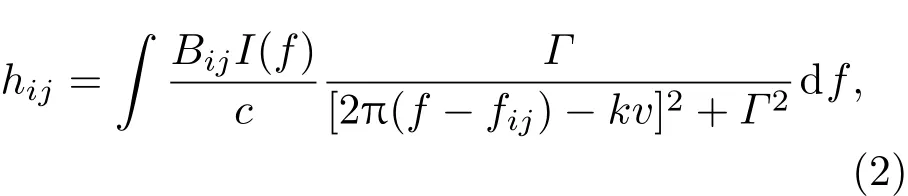
式中Bij为与受激辐射相关的爱因斯坦系数,c为光速,Γ为均匀展宽,f为激发光频率,fij为i能级跃迁至j能级时吸收光子的频率,k为波数,I(f)为激发光功率密度的谱分布,计算中认为谱分布是高斯线型[22],

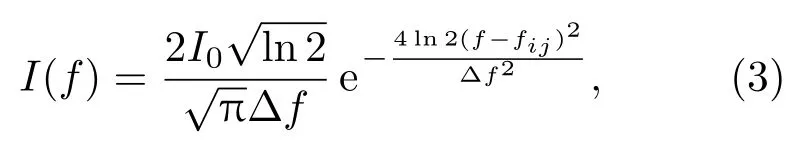
式中I0=I(f)d f,∆f为激发光功率密度谱分布的半高宽;碰撞作用因子ζij表示由于碰撞引起的原子i→j能级的跃迁以及速度大小分布的变化.

由于碰撞散射角度的不同,碰撞作用中又包含大角度散射(large angle scattering,LAS)和小角度散射(small angle scattering,SAS)两项[13,14].强碰撞模型理论认为,LAS项中原子经碰撞后的速度满足麦克斯韦分布,SAS项中原子碰撞前后速度不发生变化[13].对于原子的两个基态超精细能级,由于忽略其碰撞跃迁过程,故只有LAS项起作用.对于原子的两个激发态精细能级,碰撞作用项既包含LAS项又包含SAS项.故强碰撞模型下的速率方程可表示为[13]:

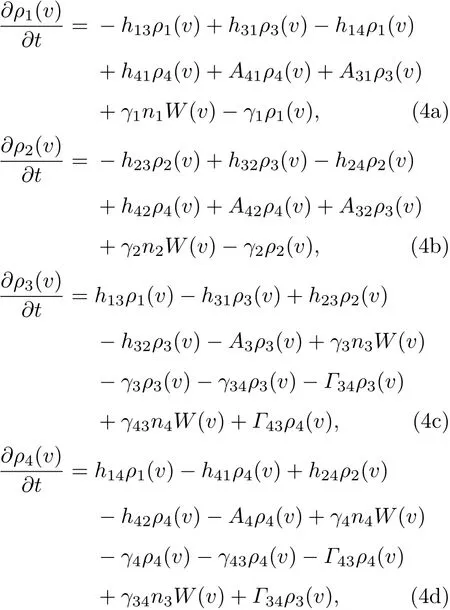
式中γij为LAS碰撞频率(γi= γii),Γij为SAS碰撞频率.ni为能级i上的总粒子数,ni=∫ρi(v)d v,各能级的粒子数密度满足归一化公式:

W(v)为一维麦克斯韦分布函数:

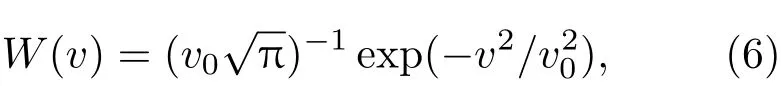
式中v0为原子的最概然速度.

强碰撞模型认为两个基态超精细结构能级上的原子具有相同的LAS碰撞频率.LAS碰撞频率γij计算公式如下:

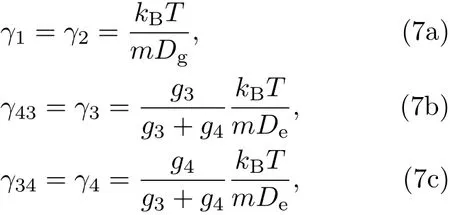
式中g3与g4分别为3,4能级的简并度,m为碱金属原子的质量,kB为玻尔兹曼常数,T为温度,Dg为基态原子的扩散系数,De为激发态原子的扩散系数.

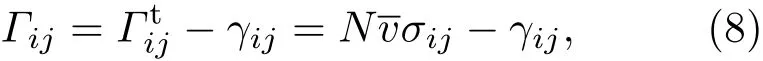
SAS碰撞频率Γij计算公式如下:式中Γitj为碰撞跃迁频率,Γitj=Nvσij;N 为缓冲气体的原子数密度;σij为由i能级至j能级的碰撞跃迁截面;v为碱金属原子与缓冲气体原子的平均运动速度.

根据漂移速率的定义,漂移速率vdr的表达式为[13]:

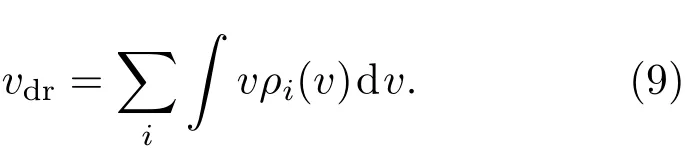
在稳态的情形下,令方程(4)中的

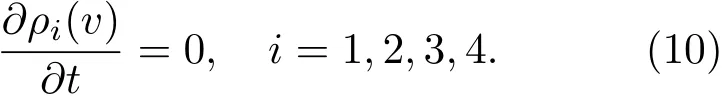
运用数值方法求解稳态条件下的速率方程(4),并结合原子数密度的归一化公式(5),可解得原子的速度分布函数ρi(v),进而可根据漂移速率的定义式(9)获得光致漂移速率vdr.

3 数值计算结果与讨论

在进行数值计算时,选择碱金属原子7Li作为研究对象,氙气作为缓冲气体.计算所采用的参数如下:中心吸收波长λ23=670.791 nm,λ24=670.776 nm,λ13=670.790 nm,λ14=670.775 nm;能级简并度g1=3,g2=5,g3=8,g4=16;A3=A4=3.77× 107s−1;σ34=1.2×10−18m2,σ43=6.6× 10−19m2. 在温度T=600 K,压强p=1.01×105Pa条件下Dg=0.77 cm2/s,De=0.52 cm2/s.

不同激发光线宽条件下光致漂移速率随激发光波长的变化曲线如图2,靠近每条曲线处的文字表示激发光线宽.由图2可以看出,无论激发光线宽如何,漂移速率随波长的变化趋势是一致的,随着波长的变化,在正方向和反方向上分别有两个漂移速率的极大值.在波长分别逐渐偏离原子的中心吸收波长670.776 nm和670.791 nm时,漂移速率的值均呈现先增大后减小的趋势,且漂移速率为极大值时对应的激发光波长也近乎一致.

光致漂移速率随激发光线宽的变化曲线如图3.由图3可以看出,随着线宽的增大,漂移速率的值呈现先增大后减小的趋势.存在一个最佳的激发光线宽,在该线宽条件下原子的漂移速率达到最大值.从光致漂移的原理出发,给出的解释如下[1,2]:单频激光只能有效激发某一特定速度附近的少量原子,具有其他速度的大部分原子则不能被有效激发,导致原子的漂移速率较低;当线宽逐渐增大时,更大速度范围内的原子会被激发,激发效率的提高使原子的漂移速率增大;但是随着线宽持续增大,在激光功率密度一定的条件下,线宽的增加会导致谱功率密度下降,使得处于激光线宽内的原子受到的激发作用减弱;此外,线宽过大也会导致反向运动的原子被激发.因此,线宽增大到一定值后,原子漂移速率开始呈现下降的趋势.由图3还可看出,最佳线宽点右侧曲线变化较左侧缓慢.该现象告诉我们,在进行相关实验时,如果激光线宽在最佳线宽附近出现不可控的波动,可以设置激发光线宽使之略大于最佳线宽,这样可以减少线宽的随机波动对漂移速率的影响.

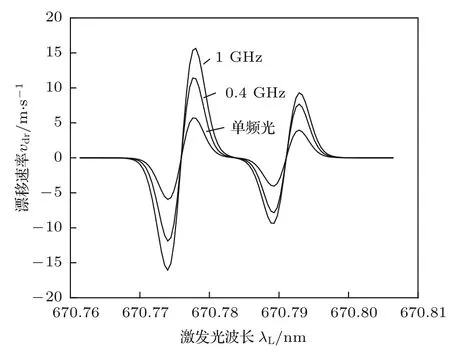
图2 不同激发光线宽条件下漂移速率随激发光波长变化曲线 计算参数为I0=0.63 W/cm2,p=300 Pa,T=600 KFig.2.Drift velocity as a function of wavelength at diff erent linewidths.Calculation parameters:I0=0.63 W/cm2,p=300 Pa,T=600 K.

不同激发光线宽条件下光致漂移速率随激发光功率密度的变化曲线如图4.靠近每条曲线处的数字表示激发光线宽的大小.由图4可知,无论线宽如何,随着功率密度的增大,漂移速率均呈现先增大后减小的趋势.当线宽增加时,获得最大漂移速率所对应的最佳功率密度逐渐减小.该现象告诉我们,在以后进行相关实验时,可采取适当增大激光线宽的方法减小最佳激光功率密度,降低激光成本.由图4还可看出,激发光线宽越小,在最佳功率密度附近漂移速率随功率密度变化越平缓.该现象告诉我们,在激光线宽较小时,激光功率密度在最佳值附近有一定偏差不会对漂移速率产生很大影响.激光线宽较大时,则需严格设置激发光功率密度.

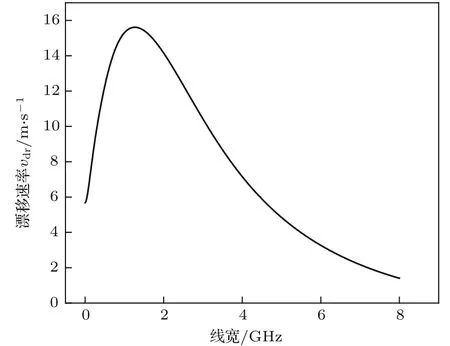
图3 漂移速率随激发光线宽变化曲线 计算参数为λL=670.78 nm,I0=0.63 W/cm2,p=300 Pa,T=600 KFig.3. Drift velocity as a function of linewidth.Calculation parameters:λL = 670.78 nm,I0=0.63 W/cm2,p=300 Pa,T=600 K.

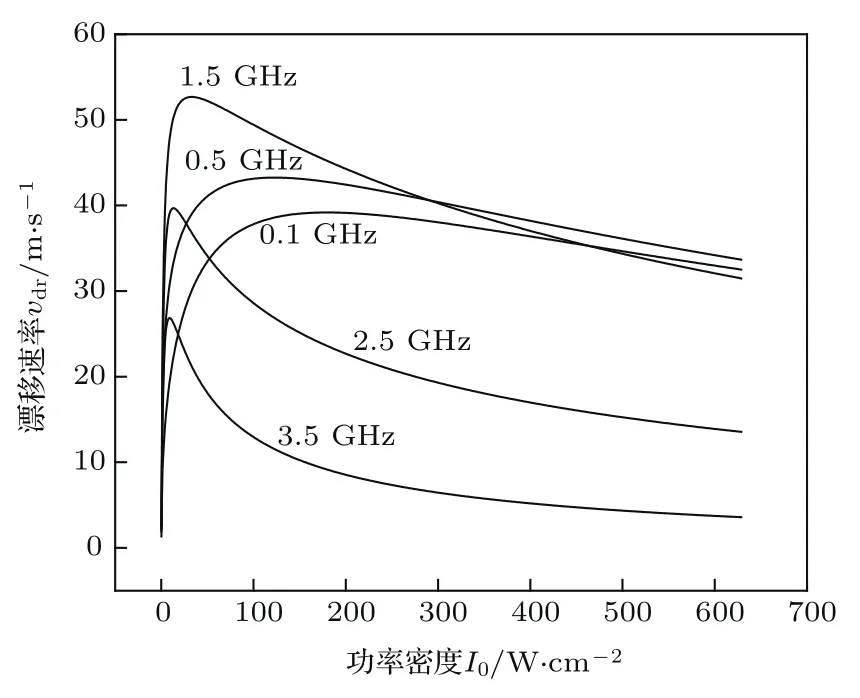
图4 不同激发光线宽条件下光致漂移速率随激光功率密度的变化曲线 计算参数为λL=670.78 nm,p=300 Pa,T=600 KFig.4.Drift velocity as a function of laser power density at diff erent linewidths.Calculation parameters:λL=670.78 nm,p=300 Pa,T=600 K.

最佳线宽随激发光功率密度的变化曲线如图5.由图5可知,在功率密度很小时,最佳线宽随功率密度的增大呈现急剧增大的趋势,待功率密度达到一定值后,最佳线宽又开始下降,且下降速度极为缓慢.

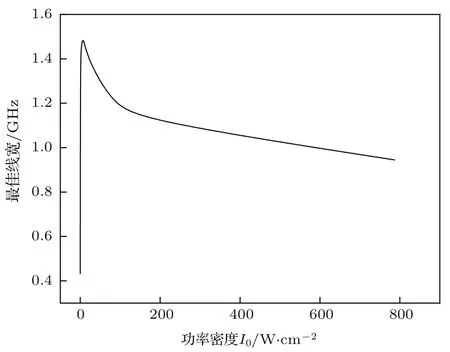
图5 最佳线宽随激发光功率变化曲线 计算参数为λL=670.78 nm,p=300 Pa,T=600 KFig.5.Best linewidth as a function of laser power density.Calculation parameters:λL=670.78 nm,p=300 Pa,T=600 K.

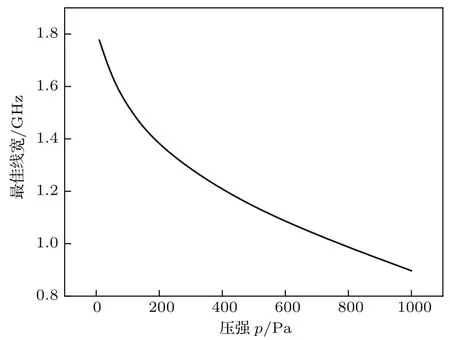
图7 最佳线宽随缓冲气体压强变化曲线 计算参数为λL=670.78 nm,I0=0.63 W/cm2,T=600 KFig.7. Best linewidth as a function of pressure.Calculation parameters:λL = 670.78 nm,I0=0.63 W/cm2,T=600 K.

最佳线宽随温度的变化曲线如图6.由图6可知,最佳线宽随着温度的升高近似线性增大.这是因为温度升高会造成原子吸收谱线多普勒展宽的增大,在总功率不变的情况下,激光需要在更宽的频率范围内分配功率才能获得最佳漂移效应.

最佳线宽随缓冲气体压强的变化曲线如图7.由图7可知,最佳线宽随着缓冲气体压强的升高而逐渐减小.且压强越高,最佳线宽下降越缓慢.该现象可以解释为:压强越低,缓冲气体与碱金属原子的碰撞频率越低,碰撞弛豫作用越弱,在总功率不变的情况下,需要增大激光线宽提升激光的速度选择性,从而获得最佳漂移效应.

4 结 论

本文在考虑激发光线宽的情况下,采用速率方程理论对碱金属原子的漂移速率进行了研究.得到以下结论:存在一个最佳的激发光线宽,在该线宽条件下原子漂移速率达到最大值;激发光功率密度、温度和缓冲气体压强会影响最佳线宽的值;在进行相关实验时,为了获得最大漂移速率,激发光应当工作在最佳线宽的条件下;当激光线宽在最佳线宽附近波动时,设置激光线宽略大于最佳线宽可减少线宽随机波动对漂移速率的影响.本文的研究结果为以后开展相关实验研究提供了理论基础,对于实验中激发光的选择具有一定的参考价值.

[1]Gel’mukhanov F K,Shalagin A M 1979 Pis’ma Zh.Eksp.Teor.Fiz.29 773

[2]Antsigin V D,Atutov S N,Gel’mukhanov F K,Telegin G G,Shalagin A M 1979 Pis’ma Zh.Eksp.Teor.Fiz.30 262

[3]Shalagin A M 1989 Sov.Phys.Usp.32 281

[4]Leiblanc F,Michaud G 1993 Astron.J.408 251

[5]Aret A,Sapar A 2002 Astron.Nachr.323 21

[6]Sapar A,Aret A,Sapar L,Poolamäe R 2009 New Astron.Rev.53 240

[7]Shalaev V M,Douketis C,Moskovits M 1992 Phys.Lett.A 169 205

[8]Chapovsky P L,Shalagin A M 1981 Opt.Commun.40 129

[9]Streater A D,Mooibroek J,Woerdman J P 1987 Opt.Commun.64 137

[10]Streater A D,Mooibroek J,Woerdman J P 1988 Appl.Phys.Lett.52 602

[11]Gangrsky Y P,Hradecny C,Slovak J,Thethal T,Yermolayev I M 1992 Phys.Lett.A 168 230

[12]Atutov S N,Kolinko P V,Shalagin A M 1993 Laser Phys.3 855

[13]Streater A D,Woerdman J P 1989 J.Phys.B:At.Mol.Opt.Phys.22 677

[14]Kryszewski S,Nienhuis G 1987 J.Phys.B:At.Mol.Phys.20 3027

[15]Dubetsky B Y 1985 Zh.Eksp.Teor.Fiz.88 1586

[16]Nienhuis G 1985 Phys.Rev.A 31 1636

[17]Gel’mukhanov F K,Il’ichov L V,Shalagin A M 1986 J.Phys.A:Math.Gen.19 2201

[18]Werij H G C,Haverkort J E M,Planken P C M,Eliel E R,Woerdman J P,Atutov S N,Chapovskii P L,Gel’mukhanov F K 1987 Phys.Rev.Lett.58 2660

[19]Haverkort J E M,Werij H G C,Woerdman J P 1988 Phys.Rev.A 38 4054

[20]Popov A K,Shalagin A M,Shalaev V M,Yakhnin V Z 1981 Appl.Phys.25 347

[21]Chai J J,Chen R S,Xu W Q 2015 Acta Optica Sin.35 0102001(in Chinese)[柴俊杰,陈日升,许文强 2015光学学报35 0102001]

[22]Zhou B K,Gao Y Z,Chen T R,Chen J H 2014 Laser Principle(Beijing:National Defence Industry Press)pp134–137(in Chinese)[周炳琨,高以智,陈倜嵘,陈家骅2014激光原理(北京:国防工业出版社)第134—137页]