基于滴水原理的关联聚类算法*

华佳林，于 剑

1.北京交通大学 计算机与信息技术学院，北京 100044

2.交通数据分析与挖掘北京市重点实验室，北京 100044

1 引言

聚类[1]是数据挖掘和机器学习中一个重要的问题，它根据某些标准将没有标定的数据分割到不同的类中。通常要进行聚类的数据以两种形式呈现[2]：特征向量或相似（相异）性矩阵。大多数的聚类算法采用特征向量作为输入，这种类型的聚类算法已有大量的文献进行研究[3]。这些研究主要集中在特征提取[4-7]和聚类方法[8-13]上，它们通常需要事先知道某些重要的参数，比如聚类的个数。

关联聚类[14]是另外一种形式的聚类问题，算法输入是一个有符号图，图中节点表示数据，节点之间由有符号边连接，即正边和负边。这种有符号图能够很好地表达现实世界中的很多场景，比如对象之间的相似/不相似、朋友/敌人、喜欢/不喜欢等。数据之间的边可以加上一个权重来表示正或负关系的程度。关联聚类的目的是使得在同一个类中的点尽可能由正边连接，而不同类中的点尽可能由负边连接。在关联聚类中不事先设定聚类的个数，而是完全由数据的内在结构所决定。

本文的主要贡献如下:

（1）提出了一种基于滴水原理的大规模有符号图收缩的方法（correlation clustering based on drop of water principle，CCDWP），基于该方法所得到的新的有符号图能极大地降低问题的规模。

（2）基于新的有符号图提出了一个关联聚类算法，算法基于图的内在结构，使用整数线性规化来对局部的点进行划分。

（3）提出的算法既保证了结果的精确性，又能够处理大规模有符号图。

（4）应用不同数据集的实验结果表明了本文提出的关联聚类算法的有效性。

2 相关工作

对于图中点的划分通常在社交媒体数据挖掘中被定义为社区发现而进行研究。通常的社区发现任务要处理的图并不考虑边的符号，对于结果的要求是社区（聚类）内部边的密度较大，社区之间边的密度较小。

关联聚类的任务包括两种情况：第一种追求最大一致性，所谓的一致性指类内正边和类间负边；第二种追求最小不一致性，所谓的不一致性指类内负边和类间正边。无论哪种情况都被证明是NP-hard问题[14]。通常的方法基于求解最小不一致性。

对于关联聚类的求解，一个自然的方法是将其表示成整数线性规化（integer linear programming，ILP）问题：

其中，w+ij和w-ij分别表示边(i,j)的正权重或负权重；xij=0表示将点i和j指派到同一个类中，xij=1表示将点i和j指派到不同的类中。约束条件xij+xjk≥xik是为了防止结果中出现不一致的情况，比如xij=xjk=0,xik=1。但是ILP通常只能处理一两百个点的网络，面对更大的网络时，时间的消耗让人难以接受。很多研究将ILP中的变量xij∈{0,1}松弛到[0,1]中，从而转化成线性规化（linear programming，LP）问题。对于新的变量的不同处理方式产生了不同的关联聚类算法[15-18]。文献[17-18]将xij看成是点之间的距离。文献[17]将距离小于阈值的两个点指派到同一个类中；而文献[18]每次从任意一个点出发构造了一个球，凡是被球所包围的点都与球心在同一个类中（称为Ball-algorithm）。而文献[16]将关联聚类问题和聚类集成问题看成是同一个问题来进行研究，同时基于文献[17]继续研究如何取得更好的阈值。而文献[15]则将1-xij看成点i和j在同一个类中的概率，当这个概率大于0.5时将对应的两个点指派到同一个类中（称为Pivot-algorithm）。Ball-algorithm和Pivot-algorithm是经典的关联聚类算法。文献[21]首先使用Fusion-Move的方法收缩有符号图，在降低数据的规模后再使用传统的关联聚类算法（文中使用Pivot-algorithm）处理新的规模更小的图。文献[22]证明了关联聚类问题如果按照最小不一致性来求解时与Multicut问题等价。

由于表达式（1）中的变量xij不是直接的类标，有些约束并没有考虑在其中，比如xii=0,导致基于LP的关联聚类算法得到的结果往往精度不高。因此在文献[17,19-20]中半正定优化（semi-definite positive，SDP）被引入来求解关联聚类问题。变量xij被重新定义为对应两个点的类标向量的内积。所谓的类标向量，比如第i个点的类标向量表示点i被指派到第k个类中，而xij=ind(i)∗ind(j)。显然矩阵X=(xij)是半正定的。文献[19-20]构建下列半正定模型：

分水岭（watersheds）算法最早被用来进行梯度图像的分割。对于一个梯度图像根据滴水原理（drop of water principle）可以构造出图像的分水岭，一个积水盆地（catchment basin）即是图像的一个分割。

本文提出的关联聚类算法借用分水岭算法的思路，首先对符号图中的点按照正度从高到低进行排序，每次对度最高的点按照正权重降低最慢寻找路径，将每个路径中的点合并成一个新的点，从而收缩图的规模。在收缩的图上选出重要的点，利用ILP来判断这些点和周围点之间的合并或分割关系，从而最终得到聚类结果。

3 基于滴水原理的符号图收缩

下面主要介绍如何借鉴滴水原理的思路来收缩大规模有符号图。

3.1 滴水原理基本定义

滴水原理在机器学习中常被用来进行图像分割处理。所谓的滴水原理是指当水从高处往下滴落时会沿着滴落速度最快的路径下落。在基于分水岭的图像分割中，滴落路径构成分水岭，从而对图像进行分割。

3.2 基于滴水原理的有符号图收缩

在关联聚类中，图中的点从聚类的意义上看重要性并不一致，其中的正度比较大的点更容易形成聚类，这些点从某种意义上可以看成聚类的原型（prototypes），因此本文从重要的点（即正度比较大的点，记为i）开始，首先将与i有正边连接的点（记为j）看作候选点，如果边(i,j)的权重是点j所有的边中权重最大的，则将i与j合并，找出所有这样的j（记为j1,j2,…,jk），这些点都与i合并成一个新的点（新点还是记为i）。记I={i,j1,j2,…,jk}，任何两个端点都在I中的边直接删除，而一个点在I中另一个不在其中的边都合并成与i相连的边，边的权重是原来边的权重相加。作者先前研究过按这种方式减小有符号图的规模的关联聚类算法并取得了不错的效果，现在将进一步减小图的规模。

基于滴水原理的有符号图收缩来自这样的一个直觉：从度较大的点出发，寻找一个正权重变化最小的路径，则路径上的点以极大的可能性属于同一个类。因此继续从j出发，寻找与j有正边连接的点（记为l），如果l与j之间的边的权重是l的所有正边中权重最大的，则将l也加入集合I；接下来继续从l出发按照上面的逻辑继续往下寻找合适的点并入I，直到不能继续往下搜索则终止。本文以一个随机产生的有符号图来说明。如图1所示，图1（a）是原始的有符号图，图中实线表示正边，虚线表示负边，边上的数字表示权重，边的粗细与权重匹配。进行简单的统计就可以知道图中的点4、15和24是比较重要的点，这几个点以极大的概率称为类原型。首先从4开始遍历，可以看到点3、5、8、9和12与4之间的边是其最大权重正边，因此I={3,4,5,8,9,12}。继续从I中的点出发，比如从3开始，发现2与3之间的边是2的所有正边中权重最大的边，因此将2并入集合I，对I中其他点进行类似的处理，最终可以得到I={1,2,3,4,5,6,7,8,9,10,11,12,13}。接下来分别从15和24出发进行类似的操作，最终形成图1（b）中所示的3个分割，每个分割是新的有符号图中的一个点，这3个点之间是合并还是分割可以转化成式（1）所示的ILP问题而获得最佳解，从而形成最终的聚类结果。上面从点i出发构造集合I的过程实际上就是从点i出发沿正边寻找权重变化最小的路径，然后将这条路径上的所有点合并成一个点，这个过程类似于滴水时的情形。

4 基于滴水原理的关联聚类算法

下面给出详细的算法过程。

算法1基于滴水原理的关联聚类算法（CCDWP）

输入：有符号图G=(V,E,W)，其中V是顶点集合，E是边集合，W是边的权重集合。

输出：聚类结果。

（1）对图中点按照正边度进行排序，对于正度最高的点i1，将所有与i1有正边连接且该正边是其所有边中权重最大的点与i1合并，产生集合I1。

（2）对集合I1中除i1之外的点沿正边寻找权重变化最小的路径，将这些路径中的点合并变成图中一个新的点，将原来的边进行合并产生新的边，两个端点都在I1中的边直接删除。

（3）将所有I1中的点、所有内部的边及所有一个端点在I1中的边及其对应的另一个端点从原来的图中删除，对剩下的图继续执行（1）和（2），直到不能找到新的点。

（4）记Θ={I1,I2,…,IN}为按照（1）~（3）所找到的N个集合，则可以得到一个收缩的有符号图G′=(V′,E′,W′)，其中

（5）每次从Θ中的一个集合出发，比如Ij，寻找所有Ij的邻居，然后按照式（1）来计算它们之间合并与否，对于不能合并的点将其作为一个新的类原型加入Θ中。继续这个过程直到所有的点都已处理完毕，这样得到的Θ即为最终的聚类结果。

在算法CCDWP中有几个地方需要声明：第一是在第（4）步中得到了N个集合，每个集合都看作是一个类原型，但是要注意的是N并不是人们认为的类个数，因为可能存在多原型的情形。另外在第（5）步中要使用到ILP，其效率比较低，通常只能处理规模为几百个点的图。因此如果Ij的邻居比较多，可能会产生超出ILP处理能力的情况。在实验中发现，大多数情形下邻居个数不会超出ILP的处理范围，而如果超出了ILP的处理范围的话也很容易处理，只需要设置一个阈值T（比如取T=200），当邻居数超过T的时候，将这些邻居与Ij之间的边的权重从大到小进行排序，ILP只处理前T个邻居，至于其他点则在以后的优化中再进行处理。这样做对于最终的聚类结果并不会产生影响，而仅仅是稍微降低了算法的速度。

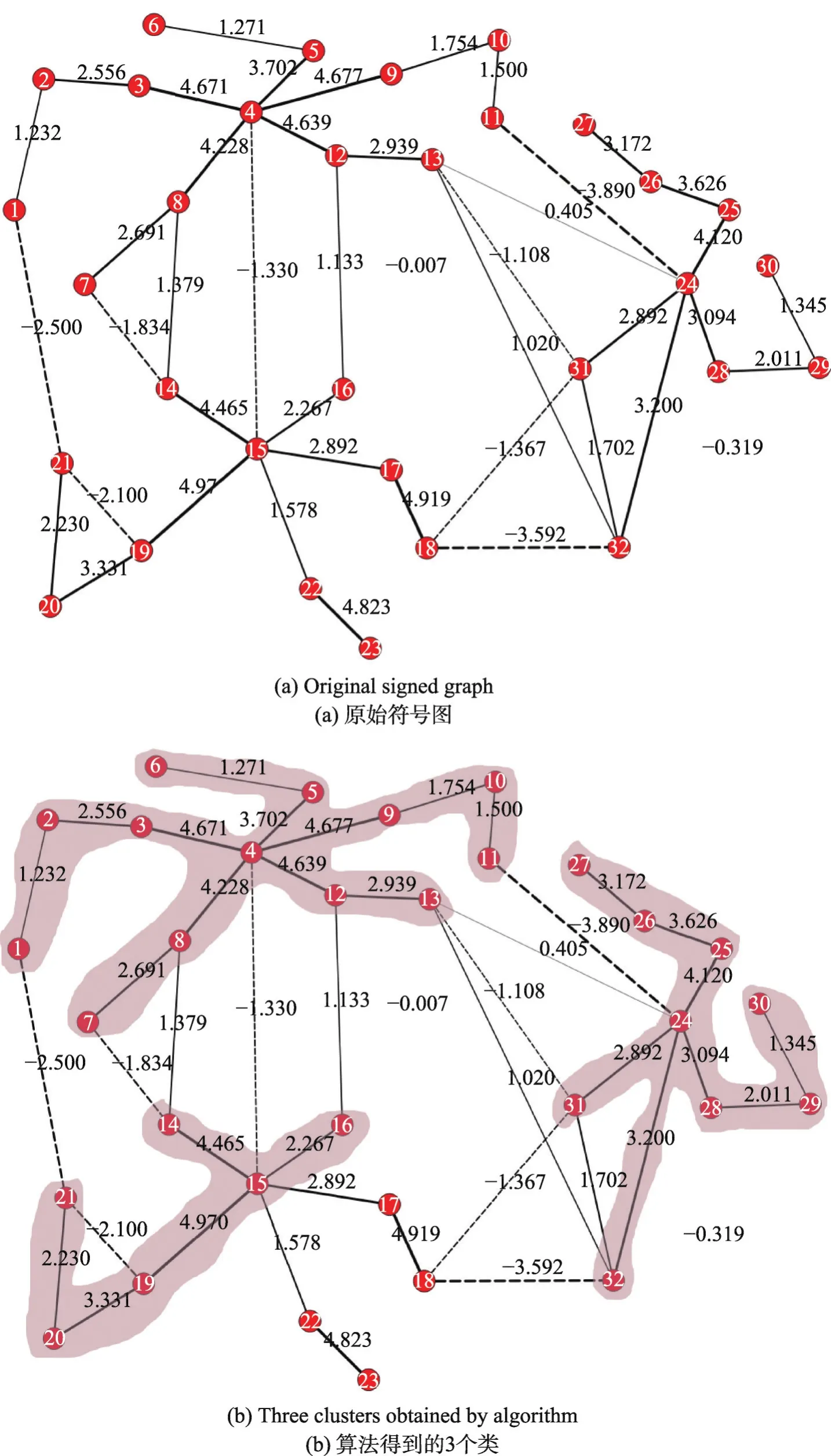
Fig.1 Original signed graph and three clusters图1 原始的符号图和形成的3个类

接下来以一个实例来详细说明算法的过程。在图2（a）所示的图中根据点的正度从高到底排序可以得到3个重要的点4、15和24。因此分布从这3个点出发按照滴水原理寻找正权重变化最小的路径。分别可以找到如下所示的路径：即图2（b）中阴影所示的部分。在这个过程中要注意选中的点所对应的边一定是权重最大的边，比如在路径4→3→2中，路径在点2即停止而没有再走下去，因为边（1,2）对应的边不是点1所有的边中权重最大的边，所以即使最后的结果是1和2同属一个类，但是为保证算法精度而不会将1纳入。这样就得到3个小的团体，将其作为3个类原型，将这些团体中的点合并成一个点，点的标示分别是4、15、24，将每个团体内部的边直接取消，外部的边进行合并，从而得到一个收缩的新的有符号图，如图2（c）所示。可以看到新的图较原来的图的规模大为缩小。接下来基于新的图继续进行处理。对于剩下的点，比如点1，发现其与33、4和15有连接，这些点之间的合并或分割的关系可以表示成式（1）的ILP问题，由于问题规模很小，可以快速进行求解。最终得到如图2（d）所示的聚类结果。

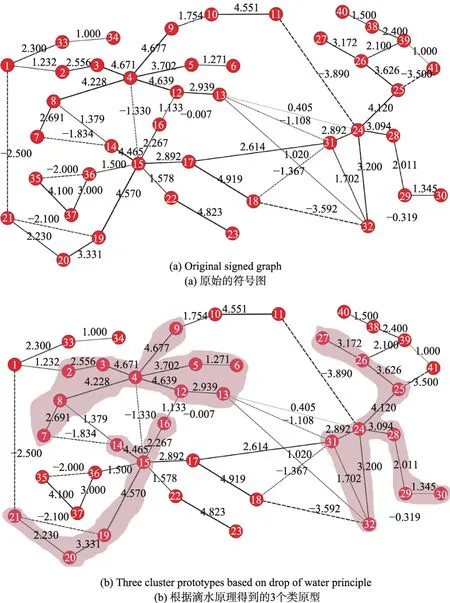
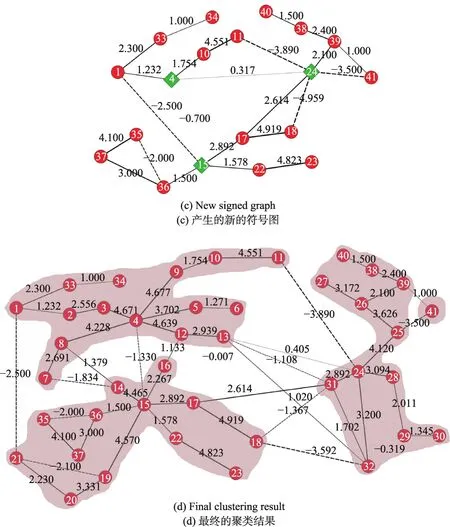
Fig.2 Procedure of CCDWP图2CCDWP算法过程

5 实验与结果

本文在人工数据和真实数据上测试算法CCDWP的有效性，并将CCDWP与Ball-algorithm[18]、Pivotalgorithm[15]、FusionCC[21]算法进行对比测试。

5.1 人工数据实验

首先设计了一个生成人工有符号图数据的算法，如算法2所示。

算法2产生有符号图

输入：点个数ND，类个数k，类内正边概率p，类内负边概率w，类间正边概率e，类间负边概率q。

输出：有符号图。

随机产生ND个点，并随机分配到k个类中。

在实验中让产生的边的权重分布在-5到5之间，然后在同种参数下产生10个随机数据运行4个算法，记录每次每个算法所产生的不一致性的数量。实验结果如图3所示。图中纵坐标表示算法结果的不一致性数量D，值越小表示算法越优。横坐标中的10个点表示10个随机产生的人工有符号图。图3（a）、（b）、（c）和（d）分别是在60个点、100个点、150个点和200个点的设置下产生的随机图。Ball-algorithm和Pivot-algorithm这两个传统的关联聚类算法，在人工数据上的实验结果与先前的研究结果一致：Ballalgorithm的结果要劣于Pivot-algorithm。FusionCC算法也是一种基于收缩的算法，毋庸置疑的是它的效果确实较以前的算法有很大的提高，但对于收缩之后所产生的新图其仍然是使用传统的关联聚类算法，比如Pivot-algorithm，也就是基于将ILP松弛为LP的优化方法。而CCDWP算法则谨慎地将图更大规模地进行收缩，对于收缩之后的图采取局部ILP优化的方法求解结果，算法没有采用降低算法精度的松弛方法，因此算法的效果要更优越，实验结果完全证明了这一点。在图3（a）中，图的规模较小，因此FusionCC和CCDWP算法对于图的收缩空间较小，同时ILP和LP的效果也相差不大。可以看到，10个随机图中有4个FusionCC的不一致性数量小于CCDWP，有4个CCDWP的不一致性数量小于FusionCC，另外两个则几乎一致。但是随着图的规模的增大，CCDWP算法中图收缩方法的优越性则越来越明显，同时局部的ILP比LP也更精确，因此在图3（b）、（c）和（d）中CCDWP算法都求得了最小的不一致性数量。

Fig.3 Experiments on synthetic data图3 人工数据实验结果

5.2 真实数据实验

本文在真实数据上继续验证CCDWP算法的效果。首先在两个小的有符号网络上验证CCDWP算法，这两个网络分别是Gahuku-Gama Subtribes（GGS）网络[23]和 Slovene Parliamentary Party（SPP）网络[24]。GGS网络表示的是16个部落之间的友好（正边）或敌对（负边）的关系。SPP网络表示的是斯洛文尼亚国会政党之间政治理念相似（正边）或不相似（负边）。CCDWP算法在这两个数据集上得到的结果如图4和图5所示，以不同的颜色表示不同的聚类。显而易见本文算法在GGS和SPP两个数据集上都给出了拥有最小不一致性的结果。

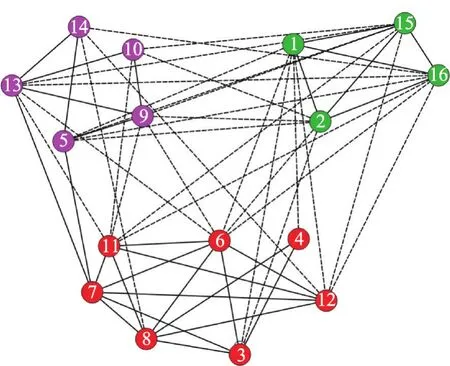
Fig.4 Clustering result of GGS图4GGS的聚类

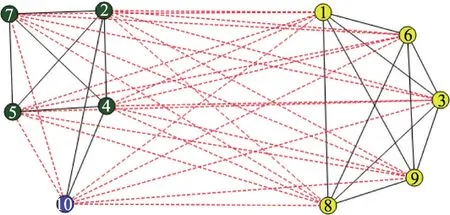
Fig.5 Clustering result of SPP图5 SPP的聚类结果

接下来继续在更大规模的真实数据上验证CCDWP算法。这些数据包括Epidermal Growth Factor Receptor pathway network（EGFR）[25]、Macrophage network（Macrophage）[26]、Yeast network（Yeast）[27]、Gene regulatory network of the Escherichia Coli（Ecoli）[28]、voting network of Wikipedia[32]，统计信息如表1所示，其中“#A”表示A的数量，比如#Vertice表示点的数量，E+和E-表示正边和负边。原始的Wikipedia数据是有向图，将其转化成无向图并按照下面的公式计算边的权重：

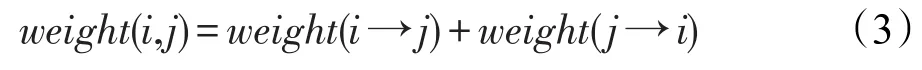
即如果原来i和j相互信任，则对应的边的权重为2，如果原来相互不信任，则对应的边的权重为-2，如果原来一个信任对方但对方不信任他，则权重为0，即没有边。

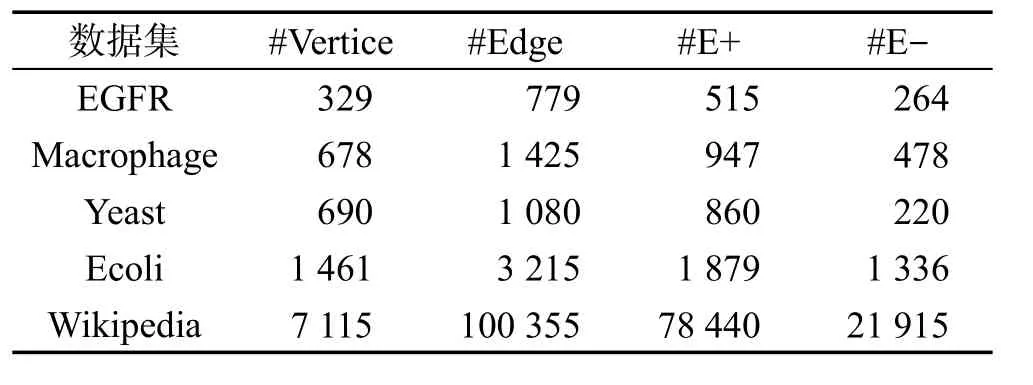
Table 1 Information of 5 real data sets表1 5个真实数据集信息

由于Ball-algorithm和Pivot-algorithm无法运行较大规模的数据，本文只对比测试了FusionCC算法和CCDWP算法，比较这两个算法给出的结果的不一致性数量，如表2所示，其中“X”表示没有结果。从真实数据的结果上看，两个算法的效果与前面人工数据上的效果类似，即当数据的规模不大，边非常稀疏时，CCDWP算法与FusionCC算法各有所长，算法的效果在一定程度上与数据的结果有关系。在5个数据集中，本文算法在EGFR和Ecoli上取得了更好的效果，在Macrophage和Yeast上两个算法取得的结果差别很小。而CCDWP算法最大的一个优势在于能够处理大规模的数据集。在运行Wikipedia数据集时，由于图的规模太大，即使在收缩之后的图上面FusionCC算法仍然难以运行。CCDWP算法则不存在这样的问题，仍然能够执行算法过程。

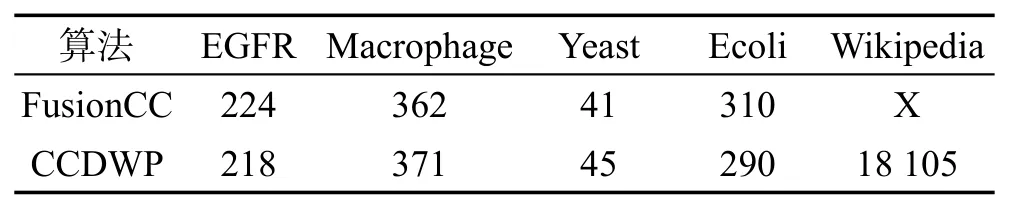
Table 2 Results of FusionCC and CCDWPin 5 real data sets表2FusionCC和CCDWP算法在5个真实数据集上的结果

6 总结

本文提出了一种基于滴水原理的关联聚类算法CCDWP。CCDWP算法根据滴水原理来搜索有符号图，将其中最有可能的路径上的点进行收缩，从而大大减小了数据规模并得到类原型。同时，本文通过巧妙地在局部执行ILP，将可能的点逐步合并到类原型中得到聚类结果。实验结果表明，本文提出的关联聚类算法在准确度和效率方面优于许多已有的关联聚类算法，因此本文算法是可行且高效的。

:

[1]Alpaydin E.Introduction to machine learning[M].Cambridge:MIT Press,2014.

[2]Yu Jian.Generalized categorization axioms[J].CoRR abs/1503.09082,2015.

[3]Xu Rui,Wunsch D C.Survey of clustering algorithms[J].IEEE Transactions on Neural Networks,2005,16(3):645-678.

[4]Wold S,Esbensen K,Geladi P.Principal component analysis[J].Chemometrics&Intelligent Laboratory Systems,1987,2(1/3):37-52.

[5]Jain A K,Duin R P W,Mao Jianchang.Statistical pattern recognition:a review[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,22(1):4-37.

[6]Hyvärinen A.Survey on independent component analysis[J].Neural Computing Surveys,1999,2(7):1527-1558.

[7]Young F W,Hamer R M.Multidimensional scaling:history,theory,and applications[M].Hillsdale:Lawrence Erlbaum Associates,1987.

[8]Jain A K,Dubes R C.Algorithms for clustering data[M].Upper Saddle River:Prentice-Hall,1988.

[9]Jain A K,Murty M N,Flynn P J.Data clustering:a review[J].ACM Computing Surveys,1999,31(3):264-323.

[10]Rodriguez A,Laio A.Clustering by fast search and find of density peaks[J].Science,2014,344(6191):1492-1496.

[11]Jain A K.Data clustering:50 years beyondK-means[J].Pattern Recognition Letters,2010,31(8):651-666.

[12]Luxburg V.A tutorial on spectral clustering[J].Statistics and Computing,2007,17(4):395-416.

[13]Parsons L,Haque E,Liu Huan.Subspace clustering for high dimensional data:a review[J].ACM SIGKDD Explorations Newsletter,2004,6(1):90-105.

[14]Bansal N,Blum A,Chawla S.Correlation clustering[J].Machine Learning,2004,56(1/3):89-113.

[15]Ailon N,Charikar M,Newman A.Aggregating inconsistent information:ranking and clustering[J].Journal of the ACM,2008,55(5):23.

[16]Gionis A,Mannila H,Tsaparas P.Clustering aggregation[J].ACM Transactions on Knowledge Discovery from Data,2007,1(1):4.

[17]Charikar M,Guruswami V,WirthA.Clustering with qualitative information[C]//Proceedings of the 44th Symposium on Foundations of Computer Science,Cambridge,Oct 11-14,2003.Washington:IEEE Computer Society,2003:524-533.

[18]Demaine E E,Immorlica N.Correlation clustering with partial information[C]//LNCS 2764:Proceedings of the 6th International Workshop on Approximation Algorithms for Combinatorial Optimization Problem and 7th International Workshop on Randomization and Approximation Techniques in Computer Science,Princeton,Aug 24-26,2003:1-13.

[19]Elsner M,Schudy W.Bounding and comparing methods for correlation clustering beyond ILP[C]//Proceedings of the Workshop on Integer Linear Programming for Natural Language Processing,Boulder,2009.Stroudsburg:ACL,2009:19-27.

[20]Mathieu C,Schudy W.Correlation clustering with noisy input[C]//Proceedings of the 21st Annual ACM-SIAM Symposium on Discrete Algorithms,Austin,Jan 17-19,2010.Philadelphia:SIAM,2010:712-728.

[21]Beier T,Hamprecht F A,Kappes J H.Fusion moves for correlation clustering[C]//Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition,Bos-ton,Jun 7-12,2015.Washington:IEEE Computer Society,2015:3507-3516.

[22]Emanuel D,Fiat A.Correlation clustering—minimizing disagreements on arbitrary weighted graphs[C]//LNCS 2832:Proceedings of the 11th Annual European Symposium on Algorithms,Budapest,Sep 16-19,2003.Berlin,Heidelberg:Springer,2003:208-220.

[23]Read K E.Cultures of the central highlands,new guinea[J].Southwestern Journal ofAnthropology,1954,10(1):1-43.

[24]Doreian P,Mrvar A.A partitioning approach to structural balance[J].Social Networks,1996,18(2):149-168.

[25]Oda K,Matsuoka Y,Funahashi A,et al.A comprehensive pathway map of epidermal growth factor receptor signaling[J].Molecular Systems Biology,2005.

[26]Oda K,Kimura T,Matsuoka Y,et al.Molecular interaction map of a macrophage[J].AfCS Research Reports,2004,2(14):1-12.

[27]Milo R,Shen-Orr S,Itzkovitz S,et al.Network motifs:simple building blocks of complex networks[J].Science,2002,298:824-827.

[28]Salgado H,Gama-Castro S,Peralta-Gil M,et al.RegulonDB(version 5.0):Escherichia coli K-12 transcriptional regulatory network,operon organization,and growth conditions[J].NucleicAcids Research,2006,34(D):394-397.