联合学习动态半参数概率图模型*

黄飞虎，陈松灿

南京航空航天大学 计算机科学与技术学院，南京 211106

1 引言

无向概率图模型是一类用于刻画一组随机变量之间条件相关性的强大统计工具，目前已被广泛应用于机器学习、计算机视觉、生物信息学与社会学等领域[1-4]。高斯图模型（Guassian graphical model，GGM）为一类流行的无向概率图模型，能很好地刻画一组正态分布随机变量的条件相关性。具体地，假设随机向量x=(x1,x2,…,xp)T∈Rp服从多元正态分布N(μ,Σ)，与之对应的无向图为G(V,E)，其中V={x1,x2,…,xp}为顶点集，E=V×V代表边集，那么对于任意(i,j)∉E，xi⊥xj|x(i,j)表示随机变量xi与xj条件独立。对于(i,j)∉E当且仅当(Σ-1)ij=0，即协方差矩阵逆（也称为精度矩阵）的(i,j)元素为0。因此，精度矩阵的稀疏模式能刻画图模型的结构。由此可知，概率图模型结构的估计可等价于稀疏精度矩阵的估计。目前已存在大量对于图模型与精度矩阵估计的工作[5-9]，它们大致可分为三类：第一类通过利用其他变量来稀疏拟合每个变量而得到每个点的近邻。例如，文献[5]通过利用套索模型（Lasso[10]）拟合每个变量而提出了近邻选择估计器，该方法可视为一种伪似然估计方法。第二类通过直接最小化ℓ1范数惩罚的负对数似然。例如，文献[3,6]通过直接求解ℓ1范数惩罚的负对数似然估计高斯图模型。文献[7]利用有效的块坐标下降方法求解该ℓ1范数惩罚的对数似然问题，提出了著名的图套索（graphical Lasso）。第三类通过利用样本协方差直接估计稀疏精度矩阵。例如，文献[8]通过求解一系列稀疏线性规划问题估计稀疏精度矩阵。文献[9]提出了一个带约束的ℓ1范数最小估计器（constrainedℓ1-minimization for inverse matrix estimation，CLIME）估计稀疏精度矩阵。

尽管GGM能很好地刻画正态分布的数据，但其要求正态分布假设过于苛刻。事实上，人们所采集到的数据往往面临两类问题：（1）数据很少严格服从正态分布；（2）数据通常含有少量噪声。为了处理问题（1），文献[11]将正态分布推广到非参数正态分布（non-parameter normal distribution，nonparanormal），进而提出了一类半参数概率图模型。具体地，如果存在一些单变量的单调可微函数{fi}p i=1，有f(x)=(f1(x1),f2(x2),…,fp(xp))T服从多元正态分布N(0,Σ)，那么x=(x1,x2,…,xp)T服从非参数正态分布NPN(0,Σ,f)。同时，由单变量函数{fi}p i=1的单调可微性，稀疏精度矩阵Σ-1同样刻画了随机变量(x1,x2,…,xp)的相关性，即给定其他变量xi与xj条件独立当且仅当(Σ-1)ij=0。为了同时解决问题（1）与（2），文献[12-13]采用基于非参排序的统计量（Spearman’s rho 或Kendall’s tau）估计相关矩阵，提出了鲁棒的估计方法用于学习半参数概率图模型。总之，这些半参图模型的估计方法的基本流程为：首先利用基于截断的正态计分（normal scoring[11]）或基于非参排序的统计量[12-13]估计出相关矩阵，然后把它代入现有图模型估计器，学习出稀疏的精度矩阵，即得到相应的图结构。

到目前为止，上述图模型的建立均基于同一分布数据，因此不适合刻画异构性或动态性的数据。例如，采集了包含正常与病状的脑影像数据[14]，如果利用上述图模型分别构建正常大脑与病状大脑的各自脑网络，则会忽略它们的共性结构；如果利用上述图模型总体估计单个脑网络，则会忽略它们之间的差异结构。因此，为了能更好地挖掘这些异构数据的结构信息，联合学习多个图模型已成为一个研究主题，典型的工作有文献[14-20]。例如，文献[15]利用层次稀疏结构惩罚能很好学习出多个图模型的共性结构。文献[16]通过利用组套索（group Lasso）[21]与两两融合套索（fused Lasso）[22]的结构惩罚学习多个图模型的共性结构，提出了联合图套索（joint graphical Lasso）。同时，文献[14]利用有序融合套索联合学习多个有序的概率图模型。为了使这些联合图模型能更好地胜任矩阵变量的数据，如脑功能性磁共振成像（functional magnetic resonance imaging，fMRI）数据及股票交易数据等，文献[20]提出了联合矩阵变量的高斯图模型。另外，针对随着时间光滑变化的异构数据，目前工作[23-25]提出了相应的动态GGM学习动态的条件相关性。总体上，这些工作均利用核光滑方法估计出相应的协方差矩阵，再把已估计的协方差矩阵代入已有的图模型估计器得到相应的动态图结构。

同样地，尽管上述联合或动态的图模型能较好地分析异构数据的条件相关性，但是它们均建立在严格的正态分布假设下。由于当前高维的异构数据通常很难严格服从正态分布且常含噪声，上述联合的与动态的图模型仍然很难胜任这些异构数据。例如，对于采集不同病状下的脑影像数据，由于疾病的易变性通常使其服从一些尾部较重的分布。另外，在采集数据过程中由于仪器不稳定，再加上志愿者头部的运动及呼吸心跳的影响，往往采集到的数据都带有一定噪声。为了处理上述问题，本文提出联合半参数图模型学习这些异构数据的条件相关性。同时，针对光滑变化的异构数据（如时序的fMRI数据），提出联合的动态半参数图模型。在建模上，将基于非参排序的相关矩阵估计方法与结构融合图套索方法相结合，提出了半参数融合图套索估计器。特别针对动态图模型，提出了一种新的核光滑Kendall’s tau相关矩阵。总之，本文主要贡献如下：

（1）提出了联合的半参数图模型用于学习非正态分布异构数据的条件相关性，且其较目前已有的联合图模型更灵活、鲁棒。

（2）进一步针对光滑变化的动态异构数据，提出了联合动态半参数图模型。

（3）采用了有效的ADMM（alternating direction method of multipliers）方法对提出的模型进行求解。

（4）利用一些人工数据与真实数据（如脑影像、股票交易数据）同时验证了模型的有效性。

2 相关工作

本文首先介绍非参数正态分布与半参数概率图模型。存在一系列单值单调且可微函数{fi}p i=1与对称正定矩阵Σ且diag(Σ)=I，那么称随机向量x=(x1,x2,…,xp)T服从非参数正态分布NPN(0,Σ,f)，当且仅当f(x)=(f1(x1),f2(x2),…,fp(xp))服从多元正态分布N(0,Σ)。文献[12-14]证明矩阵Ω=Σ-1的稀疏模式能刻画x=(x1,x2,…,xp)T的条件相关性（即Ωij=0⇔xi⊥xj|x{}i,j），且基于该非参数正态分布提出了半参数图模型。

下面介绍半参数图模型的估计方法。文献[11]提出了基于正态计分的半参数图模型估计方法，而文献[12-13]提出了一类基于非参排序方法估计该半参数模型，其不仅比基于正态计分的方法具有更优的收敛率，且更加鲁棒。具体地，首先利用基于非参排序的统计量（Spearman’s rho 或Kendall’s tau）估计相关矩阵Σ，然后将它代入已有图模型估计精度矩阵Ω=Σ-1，即半参数图稀疏结构。例如，基于非参排序的Kendall’s tau相关系数τkl估计如下：

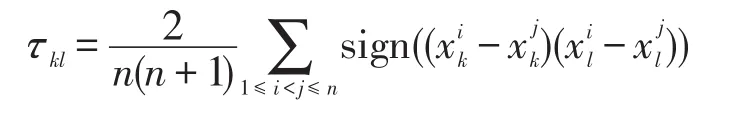
然后相关矩阵Σ=(Σkl)通过Kendall’s tau相关系数矩阵Γ̂=(τ̂kl)估计得到[26-27]，其中：

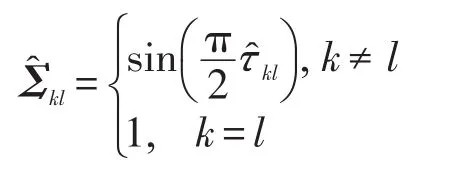
3 联合半参数图模型

下面提出联合半参数图模型用于学习非正态分布异构数据的条件相关性。该问题等价于学习多个具有一些共性结构的半参数图模型。事实上，本文研究联合半参数图模型的动机源于一些重要的应用。例如，利用一些来自同一种病多种亚型的脑影像数据[14]，通过联合学习不同病状的脑网络可挖掘出疾病的发展情况。

具体地，给定K类独立同分布样本服从非参数正态分布NPN(0,Σk,fk)，[K]={1,2,…,K}。通常为了获得稀疏的图结构，求解下面的ℓ1范数惩罚的负对数似然问题：

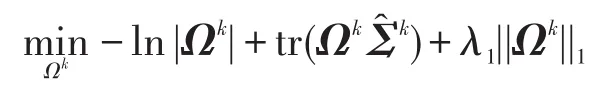
其中为的样本协方差矩阵。函数为存在且未知的隐函数，因此不能直接求得相关矩阵那么类似于文献[12-13]采用基于非参排序方法直接估计它。具体地，可通过上述Kendall’s tau统计量估计每类的相关矩阵

考虑到多个半参数图模型共享一些结构，即精度矩阵共享一些稀疏结构，因此提出了半参数融合图套索方法联合估计这些图模型。具体地，求解如下的结构正则化的负对数似然问题：

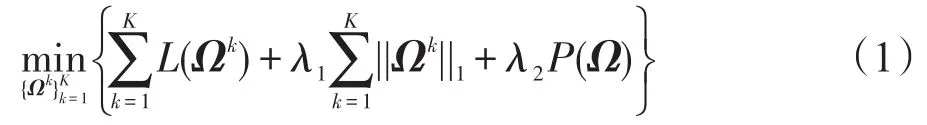
其中，为负对数似然项；为稀疏惩罚项，使得每个图模型稀疏；P(Ω)=为有序融合套索惩罚项，使得相邻的图模型更相似。这里λ1与λ2为非负的正则化参数，其中λ1控制每个图的稀疏率，而λ2控制相邻的图相似程度。当λ2=0时，问题（1）可解耦为K个稀疏正则化的负对数似然问题，那么该联合模型退化为半参数图模型[12-13]。

4 联合动态半参数图模型

下面提出联合动态半参数图模型用于学习光滑变化的非正态分布异构数据的条件相关性，其动机源于一些有意义的应用。例如，利用时序的fMRI数据学习人类不同年龄段的脑网络[25]，以了解大脑发育情况。首先，定义一类新的动态半参数概率图模型。

定义1（动态半参数图模型）如果随机变量对(X,T)服从动态半参数概率图模型，其相应的动态图为G(t)=(V,E(t))，那么其满足如下条件：

（1）X|T=t∼NPN(0,Σ(t),f)，其中T∼g(t)为定义在[0,1]上的连续函数；

（2）动态图G(t)=(V,E(t))包括固定点集合V，动态边集合E(t)，其中边的权重随着时间变量t∈[0,1]变化，且其图结构也可以随之改变，即精度矩阵Ω(t)随着时间t变化；

（3）xi⊥xj|{x{i,j},T=t}当且仅当 (i,j)∉E(t)。

人们感兴趣的时间变量T属于有界区间，因此其可以转化到区间[0,1]。不失一般性，本文均假设t∈[0,1]。接下来，为了估计该动态半参数图模型，利用一种新的核光滑Kendall’s tau相关系数矩阵Γ(t)=(τkl(t))。具体地，当每个时间点t∈[0,1]（即每个分布）只采一个样本时，核光滑Kendall’s tau相关系数τkl(t)估计如下：

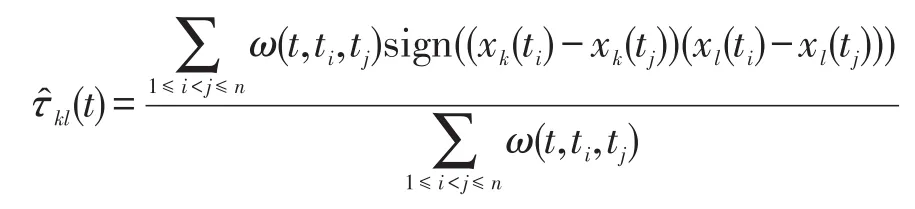
其中，ω(t,ti,tj)=Kh(t-ti)Kh(t-tj)。

当每个时间点t∈[0,1]采m≥2个独立同分布样本时，核光滑Kendall’s tau相关系数τkl(t)估计如下：

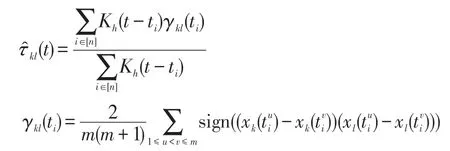
这里，Kh(·)=K(·/h)为对称核函数，其中h>0 为带宽参数。例如，高斯核，其中带宽参数h控制围绕时间点ti的窗口。具体地，较小的h表明估计的图模型随时间变化的频率较高，而较大的h表明估计的图模型随时间变化的频率较低。然后，相关矩阵Σ(t)由核光滑Kendall’s tau相关系数矩阵Γ̂(t)=(τ̂kl(t))估计可得，具体为：

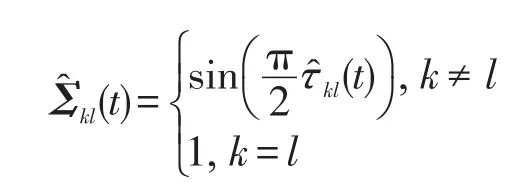
最后，把已估计出的相关矩阵代入已有的图模型估计器（如graphical lasso[7]或CLIME[9]）可以得到稀疏精度矩阵Ω(t)，即动态图结构。

考虑到动态图模型随着时间变化依然保持一定的共性结构，本文采用上文的联合学习思想，提出联合的动态半参数图模型。具体为，把已估计出的相关矩阵 {Σ̂(tk)}K k=1代入上文提出的半参数融合图套索估计器（1），可以联合估计多个时间点的精度矩阵即稀疏图结构。

5 模型优化

本文利用交替方向乘子方法（ADMM[28]）求解问题（1）。ADMM是一类非常适用于求解带等式约束问题的优化方法，可表示如下：

其中，λ为拉格朗日乘子；ρ为惩罚参数。首先给出上述问题（2）的增广拉格朗日函数：

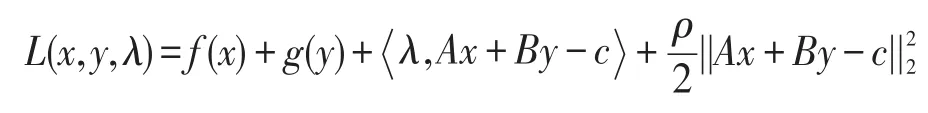
那么ADMM采用Gauss-Seidel迭代求解问题（2），在第t+1步迭代表示如下：

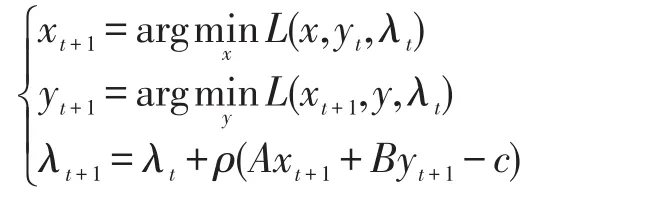
下面应用ADMM具体求解问题（1）。首先把问题（1）改写为如下等式约束问题：

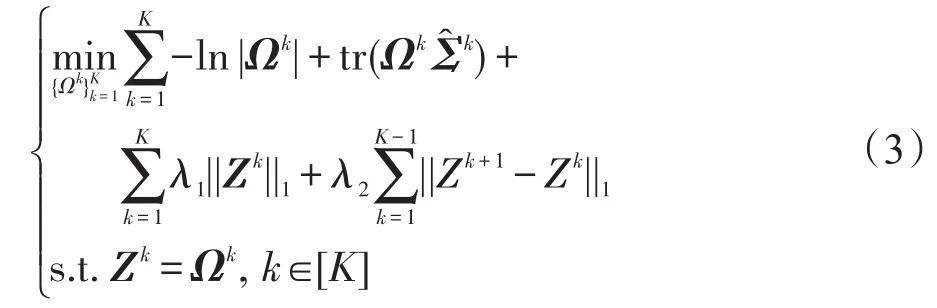
问题（3）的增广拉格朗日函数可表示如下：

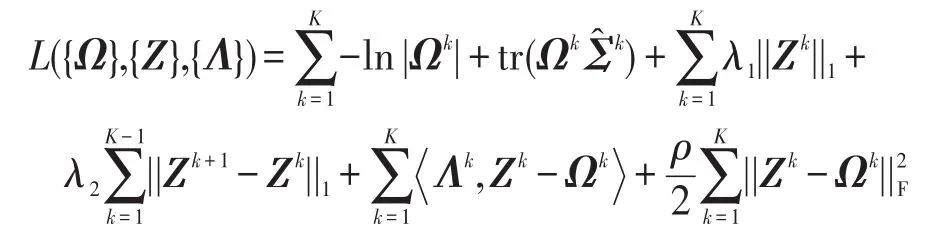
然后利用ADMM求解问题（3），在第t+1步迭代表示如下：

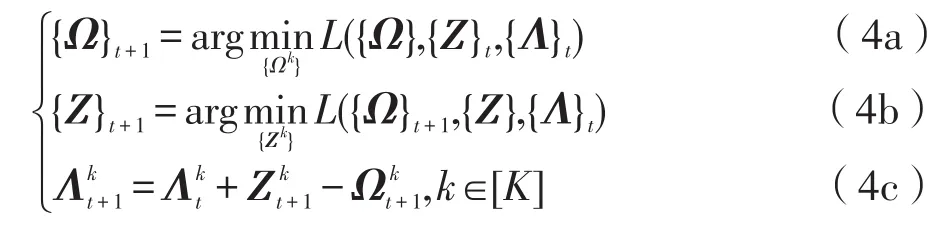
接下来，将分别介绍问题（4a）与（4b）的具体求解。首先对于问题（4a），其可以分解为K个独立问题。对于k∈[K]：

然后对其目标函数微分得到：

易知Ωk与矩阵Ak=Σ̂k-Λk-ρZk共享特征向量，且其特征值满足如下关系：

其中，{αi}ip=1为矩阵Ωk的特征值；{βi}ip=1为矩阵Ak的特征值。因此，对矩阵Ak进行特征值分解为Ak=UkBkUk，那么可得Ωk=UkDkUk，其中Dk为特征值{αi}ip=1组成的对角矩阵。

同样，问题（4b）可以分解p2个独立的融合套索问题。

对于1≤i,j≤p：

且子问题（5）可用标准融合套索的近似算子求解[29]。由于{Zk}为对称矩阵，只要求解个子问题（5）。由于问题（4a）与（4b）均可分解为独立的子问题，可以考虑利用并行框架来加速本文算法。

6 人工数据实验

下面利用一些人工数据验证本文模型的有效性。具体地，对于学习异构数据的条件相关性，即学习多个半参数概率图模型（semi-parameter probability graphical model，SPGM），本文的联合半参数图模型（joint semi-parameter graphical Lasso，JSPGL）将与标准的半参数图模型[12-13]（semi-parameter graphical Lasso，SPGL）及联合的GGM[14,16]（joint graphical Lasso，JGL）比较。对于动态的异构数据条件相关性，即学习多个动态半参数概率图模型（dynamic semi-parameter probability graphical model，DSPGM），本文的联合动态半参数图模型（joint dynamic semi-parameter graphical Lasso，JDSPGL）将与动态半参数图模型（dynamic semiparameter graphical Lasso，DSPGL）及动态的GGM[21-23]（dynamical graphical Lasso，DGL）比较。

在实验中，为了突出本文模型的有效性，让DGL与融合图套索框架结合来参与比较。文中所有模型参数通过十重交叉验证得到。同时，所有实验均重复50次，下面报告的实验结果为其平均值。另外，上述所有动态图模型，均选择带宽参数h=1。最后，所有算法均在Matlab软件平台上运行，且在英特尔i5-3470处理器、16 GB内存的计算机上执行。

6.1 人工数据的生成

本节介绍一些人工数据的生成。不失一般性，本文只关注学习Erdös-Rényi（ER）网络。具体地，首先生成一个稀疏率92%的ER网络，然后由生成的ER网络复制K份，再对每个网络随机减少p/4个边，最后得到多个具有一定相似结构的网络，其相应的链接矩阵为为了使得这些链接矩阵符合精度矩阵，进行如下赋值：

其中，Ek,k∈[K]表示图边集合。最后，在矩阵的对角元素加上相应的正数以保证它们对称正定。为了方便，令n=n1=n2=…=nK。接下来，让每个正态分布生成n个数据点为了验证本文模型对正态分布假设的放松，与文献[12]类似，再对数据进行高斯累积分布函数转化，如下：

其中为标准的高斯累积分布函数。因此，得到转化数据服从非参数正态分布f)，k∈[K]。

下面介绍产生动态半参数图模型的过程。同样地，首先生成一个稀疏率92%的ER网络，然后由生成的ER网络复制n个，再对每个网络随机减少p/4个边，最后得到多个具有一定相似结构的网络，其相应的链接矩阵为为了使得这些链接矩阵符合动态结构，对其进行如下赋值：

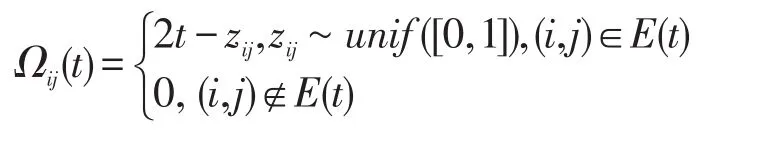
其中，t∈[0,1]。同时在矩阵{Ω(tk)}n k=1的对角元素加上相应的正数以保证它们对称正定。接下来，让每个正态分布N(0,Ω(tk)-1)，k∈[n]生成1个数据点xk。因此，得到一些独立非同分布的样本{xk}n k=1，即每个样本服从各自的分布。同样地，与上述类似把它们转化为独立非同分布的样本{yk}n k=1，即它们服从NPN(0,(Ωk)-1,f)。

6.2 评价标准

本节给出对图模型结构恢复的真阳性率（TPR）与假阳性率（FPR）来评价所有模型的性能。假定为已估计出的稀疏精度矩阵为真实的精度矩阵，给出指标TPR与FPR的定义如下：

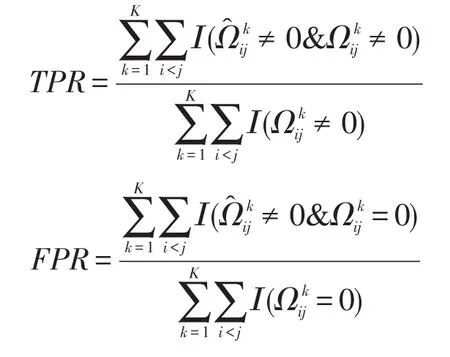
其中，为指标函数。同时，为了验证本文模型的鲁棒性，考虑对这些人工数据加一些噪声。具体地，在每个样本矩阵随机选取[nr]个元素用5或-5代替，其中0≤r≤1为噪声率。

6.3 实验结果

在实验中，利用4个半参数概率图模型的学习作为评估模型效果，即K=4。同时，对于动态半参数概率图模型的学习在n个时间点随机选取4个时间点联合估计作为评估模型效果。

由图1可知，在学习非正态分布异构数据的相关性时，本文的JSPGL优于JGL与SPGL，也更加鲁棒。由图2可知，本文联合模型在小样本情况下依然优于JGL与SPGL。由图3可知，在学习动态的非正态分布异构数据的相关性时，本文的JDSPG优于DSPGL与DGL，也更加鲁棒。同样地，由图4可知，本文联合动态图模型在小样本情况下依然优于其他方法。从图3、图4可知，JDSPGL并非很显著地优于DSPGL。由于这两种方法估计相关性矩阵Σ(t)均用核光滑方法，它们在估计相关性矩阵时已经把每个时间点的信息考虑进去了，即已经用了联合学习思想。

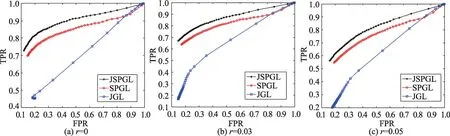
Fig.1 ROC curves of estimating multiple SPGMs at different noise contamination levels(n=200 and p=200)图1 多个半参数图模型在不同程度噪声污染下估计的ROC曲线（n=200与p=200）

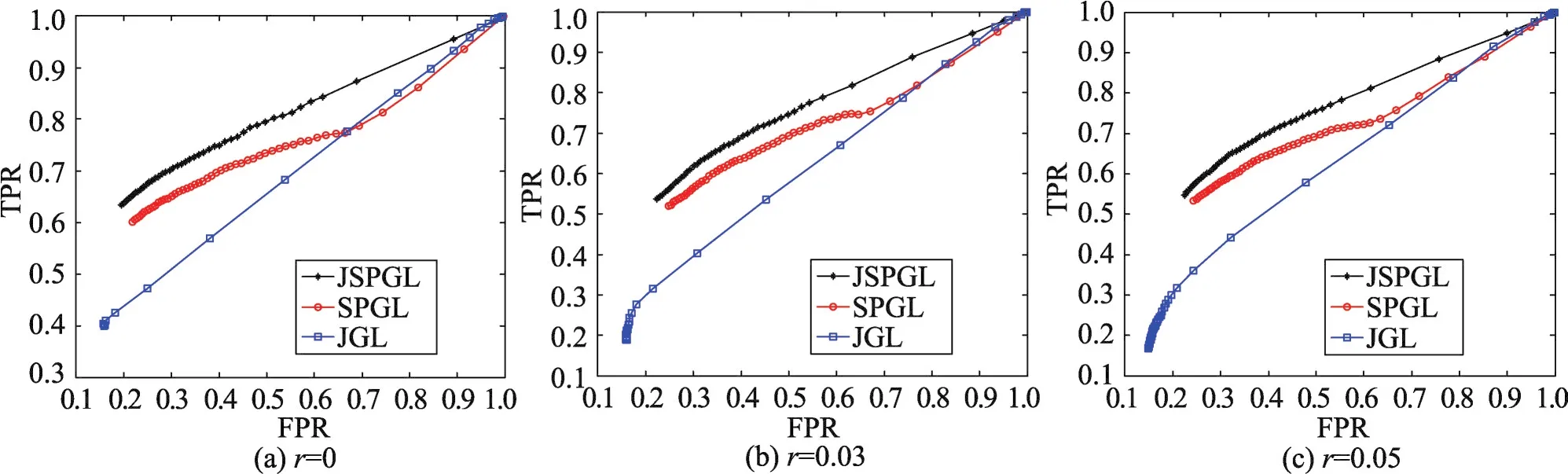
Fig.2 ROC curves of estimating multiple SPGMs at different noise contamination levels(n=100 and p=200)图2 多个半参数图模型在不同程度噪声污染下估计的ROC曲线（n=100与p=200）

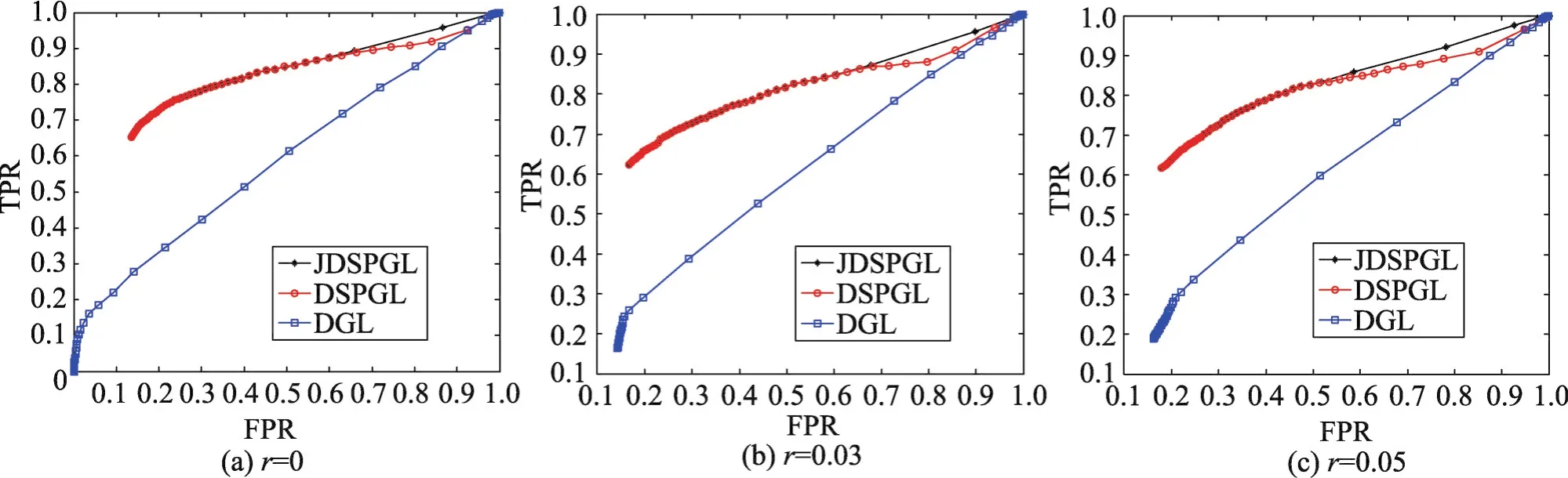
Fig.3 ROC curves of estimating DSPGMs at different noise contamination levels(n=200 and p=200)图3 动态半参数图模型在不同程度噪声污染下估计的ROC曲线（n=200与p=200）

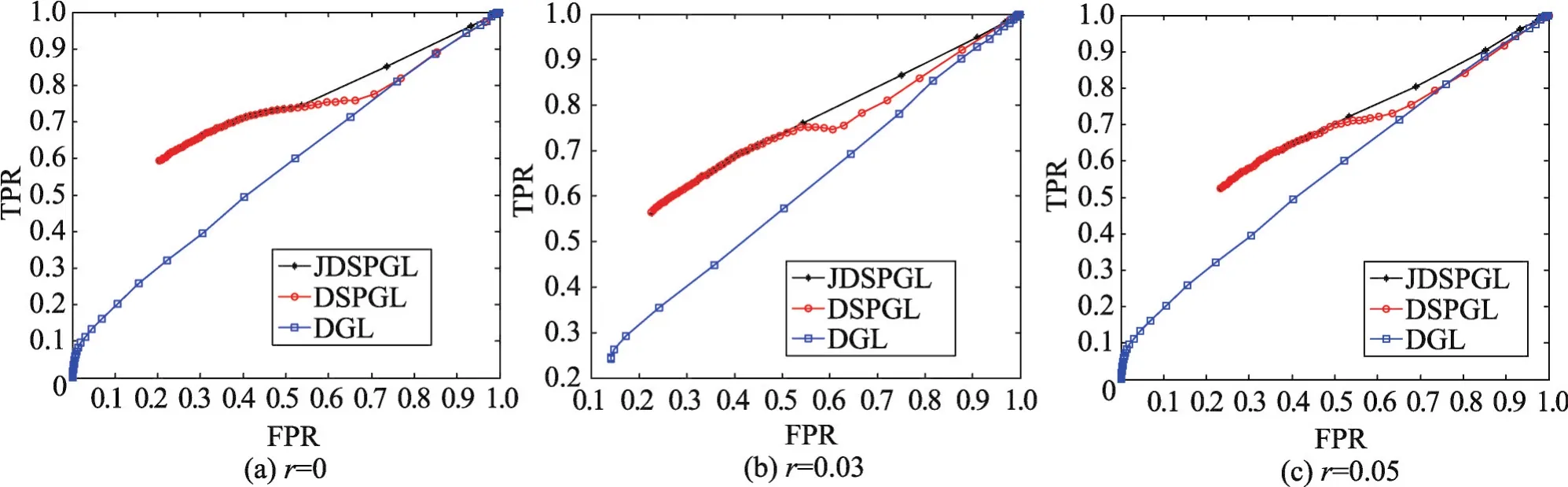
Fig.4 ROC curves of estimating DSPGMs at different noise contamination levels(n=100 and p=200)图4 动态半参数图模型在不同程度噪声污染下估计的ROC曲线（n=100与p=200）

7 真实数据实验

本文利用真实的脑影像数据与股票交易数据分别验证提出的联合半参数图模型（JSPGL）与联合动态半参数图模型（JDSPGL）的有效性。

脑影像数据（http://adni.loni.ucla.edu/）采集于32个老年痴呆（Alzheimer’s disease，AD）大脑、71个认知障碍（mild cognitive impairment，MCI）大脑与62个正常（normal control，NC）大脑，且所有数据包括116个特征，每个特征代表每个解剖兴趣区域。对于脑影像数据，将利用JSPGL联合构建三类大脑网络，其为AD脑网络、MCI脑网络与NC脑网络。通过估计这些脑网络找到它们的共性与差异（见图5）。

股票交易数据（http://finance.yahoo.com/）收集于标准普尔500指数公司从2003年1月到2008年1月每天股票交易数据。该数据包括452家公司的1 258条收盘价格。考虑到该股票交易数据随着时间较光滑变化，本文利用JDSPGL学习这452家公司在股票交易中动态的条件相关性。

这些真实数据没有已知的结构信息，因此本文类似于文献[7]利用Kullback-Leible（KL）损失定量地验证模型估计的性能。对于多类数据如脑影响数据，首先把每类数据[nk]划分为M份{D1,D2,…,DM}，然后定义KL-loss如下：

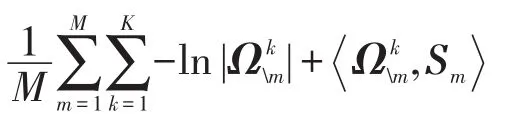
其中，是在训练样本（[nk]减去Dm）上估计得到的；Sm为测试样本Dm的样本协方差矩阵。对于动态数据如股票交易数据，首先把所有数据[n]划分为{D1,D2,…,DM}，然后定义KL-loss如下：

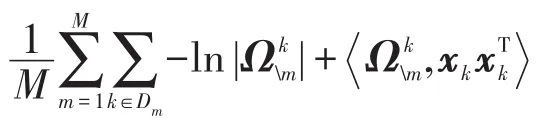
其中是在训练样本（[n]减去Dm）上估计得到的。

由表1可知，在脑影像数据实验上，本文JSPGL的性能优于SPGL与JGL。同时，由图5可知，NC脑网络与MCI脑网络的差异要小于NC脑网络与AD脑网络，因此JSPGL学习得到的脑网络同时具有较好的解释性。由表2可知，在股票交易数据上，本文JDSPGL的性能优于DSPGL与DGL。

Table 1 5-flod KL-loss on brain imaging dataset表1 图模型在脑影像数据上的5重KL-loss

Table 2 5-flod KL-loss on stock trading dataset表2 图模型在股票数据上的5重KL-loss

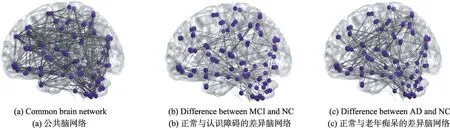
Fig.5 Brain networks estimated by joint semi-parameter graphical model图5 联合半参数图模型估计的脑网络

8 总结

本文提出了联合半参数概率图模型用于学习非正态分布异构数据的条件相关性。同时，针对光滑变化的异构数据，提出了联合动态半参数图模型。将基于非参排序的相关矩阵估计方法与结构融合图套索方法相结合，提出了一类半参数融合图套索方法来估计提出的模型。特别针对动态半参数图模型，提出了一种新的核光滑Kendall’s tau相关矩阵。由于放宽了正态分布的假设，使得本文模型比当前联合高斯图模型更灵活。由于采用了基于非参排序的相关矩阵估计方法，使得本文模型更鲁棒。在未来工作中，将提出的联合动态图模型推广到混合变量的半参数图模型[30]。

：

[1]Lauritzen S L.Graphical models[M].Oxford:Oxford University Press,1996.

[2]Liu Jianwei,Cui Lipeng,Luo Xionglin.Survey on the sparse learning of probabilistic graphical model[J].Chinese Journal of Computers,2016,39(8):1597-1611.

[3]Banerjee O,Ghaoui L E,d'Aspremont A.Model selection through sparse maximum likelihood estimation for multivariate Gaussian or binary data[J].Journal of Machine Learning Research,2008,9:485-516.

[4]Huang Shuai,Li Jing,Sun Liang,et al.Learning brain connectivity of Alzheimer’s disease from neuroimaging data[C]//Proceedings of the 23rd Annual Conference on Neural Information Processing Systems,Vancouver,Dec 7-10,2009.Red Hook:CurranAssociates,2009:808-816.

[5]Meinshausen N,Bühlmann P.High-dimensional graphs and variable selection with the Lasso[J].The Annals of Statistics,2006,34(3):1436-1462.

[6]Yuan Ming,Lin Yi.Model selection and estimation in the Gaussian graphical model[J].Biometrika,2007,94(1):19-35.

[7]Friedman J,Hastie T,Tibshirani R.Sparse inverse covariance estimation with the graphical Lasso[J].Biostatistics,2008,9(3):432-441.

[8]Yuan Ming.High dimensional inverse covariance matrix estimation via linear programming[J].Journal of Machine Learning Research,2010,11:2261-2286.

[9]Cai T,Liu Weidong,Luo Xi.A constrainedℓ1 minimization approach to sparse precision matrix estimation[J].Journal of the American Statistical Association,2011,106(494):594-607.

[10]Tibshirani R.Regression shrinkage and selection via the Lasso[J].Journal of the Royal Statistical Society:Series B Methodological,1996,58(1):267-288.

[11]Liu Han,Lafferty J D,Wasserman LA.The nonparanormal:semiparametric estimation of high dimensional undirected graphs[J].Journal of Machine Learning Research,2009,10(3):2295-2328.

[12]Liu Han,Han Fang,Yuan Ming,et al.High-dimensional semiparametric Gaussian copula graphical models[J].The Annals of Statistics,2012,40(4):2293-2326.

[13]Xue Lingzhou,Zou Hui.Regularized rank-based estimation of high-dimensional nonparanormal graphical models[J].The Annals of Statistics,2012,40(5):2541-2571.

[14]Yang Sen,Lu Zhaosong,Shen Xiaotong,et al.Fused multiple graphical Lasso[J].SIAM Journal on Optimization,2015,25(2):916-943.

[15]Guo Jian,Levina E,Michailidis G,et al.Joint estimation of multiple graphical models[J].Biometrika,2011,89(1):1-15.

[16]Danaher P,Wang Pei,Witten D M.The joint graphical Lasso for inverse covariance estimation across multiple classes[J].Journal of the Royal Statistical Society:Series B Statistical Methodology,2014,76(2):373-397.

[17]Zhu Yunzhang,Shen Xiaotong,Pan Wei.Structural pursuit over multiple undirected graphs[J].Journal of the American StatisticalAssociation,2014,109(508):1683-1696.

[18]Lee W,Liu Yufeng.Joint estimation of multiple precision matrices with common structures[J].Journal of Machine Learning Research,2015,16:1035-1062.

[19]Cai T,Li Hongzhe,Liu Weidong,et al.Joint estimation of multiple high-dimensional precision matrices[J].Statistica Sinica,2016,26(2):445-464.

[20]Huang Feihu,Chen Songcan.Joint learning of multiple sparse matrix Gaussian graphical models[J].IEEE Transactions on Neural Networks and Learning Systems,2015,26(11):2606-2620.

[21]Yuan Ming,Lin Yi.Model selection and estimation in regression with grouped variables[J].Journal of the Royal Statistical Society:Series B Statistical Methodology,2006,68(1):49-67.

[22]Tibshirani R,Saunders M,Rosset S,et al.Sparsity and smoothness via the fused Lasso[J].Journal of the Royal Statistical Society:Series B Statistical Methodology,2005,67(1):91-108.

[23]Zhou Shuheng,Lafferty J D,Wasserman LA.Time varying undirected graphs[J].Machine Learning,2010,80(2):295-319.

[24]Kolar M,Xing E P.On time varying undirected graphs[C]//Proceedings of the 14th International Conference on Artificial Intelligence and Statistics,Fort Lauderdale,Apr 11-13,2011:407-415.

[25]Qiu Huitong,Han Fang,Liu Han,et al.Joint estimation of multiple graphical models from high dimensional time series[J].Journal of the Royal Statistical Society:Series B Statistical Methodology,2016,78(2):487-504.

[26]Fang Hongbin,Fang Kaitai,Kotz S.The meta-elliptical distributions with given marginal[J].Journal of Multivariate Analysis,2002,82(1):1-16.

[27]Kruskal W H.Ordinal measures of association[J].Journal of the American Statistical Association,1958,53(284):814-861.

[28]Boyd S,Parikh N,Chu E,et al.Distributed optimization and statistical learning via the alternating direction method of multipliers[J].Foundations&Trends in Machine Learning,2011,3(1):1-122.

[29]Hoefling H.A path algorithm for the fused Lasso signal approximator[J].Journal of Computational and Graphical Statistics,2010,19(4):984-1006.

[30]Fan Jianping,Liu Han,Ning Yang,et al.High dimensional semiparametric latent graphical model for mixed data[J].Journal of the Royal Statistical Society:Series B Statistical Methodology,2017,79(2):405-421.

附中文参考文献:

[2]刘建伟,崔立鹏,罗雄麟.概率图模型的稀疏化学习[J].计算机学报,2016,39(8):1597-1611.