分布载荷作用下多铁性圆柱复合材料的断裂分析

张 俊， 靳 莹， 朱炳任

(陆军装甲兵学院车辆工程系， 北京 100072)

多铁性复合材料在生物医疗、精密控制、信息传输与存储等工程实践中被广泛应用，其优越的力电耦合性能受到越来越多研究者的关注[1-3]。但由于材料本身大都为脆性的人工陶瓷，因此在复杂的工作环境下容易产生缺陷、裂纹，并导致多铁性元器件失效[4]。通过分析研究多铁性复合材料的各项参数对其断裂行为的影响，能够为该类复合材料的优化设计和性能改善提供重要的理论参考。近年来，对该类材料的断裂分析研究已取得较大进展，但在建立断裂力学分析模型时，大部分研究者会把模型上载荷的作用方式假设成存在于裂纹面上的等效载荷，或是存在于模型外表面上的均布载荷[5-7]，这与实际工作时材料外表面往往存在着局部的非均布载荷不相符。因此，研究外表面分布载荷作用下多铁性复合材料的断裂力学问题更具有现实意义。

鉴于此，笔者在建立断裂力学分析模型的基础上，利用分离变量法和无穷级数法推导出该模型的Cauchy奇异积分方程组，并采用配点法对其进行数值求解，分析讨论出不同参数对裂纹尖端应力强度因子(Stress Intensity Factor,SIF)的影响规律，以期对多铁性复合材料的防断裂优化设计提供一定的参考。

1 理论模型

图1为分布载荷作用下某一压电/压磁圆柱复合材料的横截面。其中：内部为压磁层，外部为压电层，层间存在一条弧形裂纹，外表面作用有一段轴向分布载荷。建立坐标系，以横截面圆心为坐标原点O，x轴正方向水平向右，y轴垂直于x轴向上，z轴方向根据右手螺旋法则确定。由图1可知：压磁层和压电层的厚度分别为r1-r0及r2-r1；裂纹上下尖端所对应的中心角分别为α和γ，则裂纹弧长可表示为l=(α-γ)r1；令分布载荷密度函数为τ(θ)，其中θ∈[θR,θL]。

假设图1中各材料沿z轴方向极化，通过压电理论容易知道该圆柱复合材料为横观各向同性材料，且横截面内的电磁场与轴向变形相耦合。为方便起见，用i=1,2分别表示压磁层和压电层，则该材料的基本方程可表示为

(1)

(2)

(3)

由于Mi可逆，将式(1)代入式(2)可得

(4)

在断裂力学分析中，该模型为电磁可通模型,其边界条件可表示为

(5)

(6)

(7)

(8)

w1(r1,θ)=w2(r1,θ)，θ∉(γ,α)；

(9)

(10)

式中：H(·)为Heaviside函数。

2 断裂力学分析

在运用边界条件时，利用正余弦函数的正交性将位移、磁势、电势、剪切应力、磁感应强度以及电位移分为奇部和偶部来处理。对于边界条件(6)，当利用正余弦函数的正交性将其转化为代数方程时，会因τ(θ)的不同而得到不同的表达式，因此在根据边界条件求解代数方程组之前，首先需要确定τ(θ)的表达式，也即确定分布载荷的分布形式。分布载荷的3种不同分布形式为：

1) 当层合柱外表面受均布载荷作用时，有τ(θ)=τ0，其中τ0为分布范围内任一点处的单位载荷；

2) 当层合柱外表面受正弦型分布载荷作用时，有τ(θ)=τ0sin[(θ-θR)π/(θL-θR)]；

3) 当层合柱外表面受余弦型分布载荷作用时，有τ(θ)=τ0cos[(θ-θR)π/(θL-θR)]。

2.1 位错密度函数

通过位错模拟法得到相应的位错密度函数为

(11)

显然，边界条件(9)满足式(11)。此外，为使位移场满足单值性要求，位错密度函数还需满足的条件为

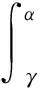
(12)

利用分离变量法求解式(4)，可得到其无穷级数解析式的表达式，再代入式(11)可得

(13)

利用正余弦函数的正交性，式(13)可改写为

(14)

通过边界条件可知,奇部和偶部具有相同的系数矩阵Ω，于是可得

(15)

式中：Ω为12阶矩阵；P=[P1P2]T, 其中

对于SP(n)和ST(n)，可以根据不同类型的分布载荷τ(θ)的表达式得到，即

1) 当层合柱外表面为均布载荷时，有

SP(n)=(sin(nθL)-sin(nθR))/n；
ST(n)=(cos(nθR)-cos(nθL))/n。

2) 当层合柱外表面为正弦型分布载荷时，有

3) 当层合柱外表面为余弦型分布载荷时，有

于是求解式(15)，可以解得系数矩阵P和Q分别为

(16)

式中：Λ1、Λ2分别为Ω-1的第1、2列向量。

2.2 Cauchy奇异积分方程组

将式(16)代入式(10)，化简整理可得

(17)

式中：

其中Λ12、Λ22、Λ32、Λ42均为列向量Λ2中的元素；

其中

Λ11、Λ21、Λ31、Λ41均为列向量Λ1中的元素。

通过计算可知

(18)

式中：q为常数。将式(18)代入式(17)，利用

可得

(19)

式中：

其中ϑ=cosθ，ζ=coss。

令f(ζ)≡g(s)cscs,a=cosα,b=cosγ, 则ds=-cscsdζ，将其代入式(19)可得

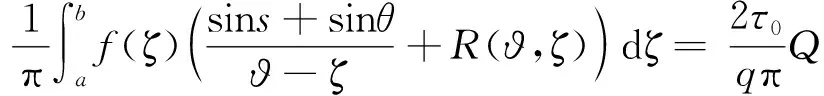
(20)

(21)

式中：

根据Cauchy奇异积分方程理论，可将式(21)的解表示为

(22)

利用式(22)可通过配点法将式(21)转化为如下代数方程组

(23)

式中：m为求积节点数，其值将依据数值计算收敛速度的大小来确定；

2.3 应力强度因子

根据Ⅲ型裂纹的应力强度因子的定义可得

(24)

式中：

(25)

为裂纹尖端的奇异应力。

将ζ=coss, ϑ=cosθ,a=cosα,b=cosγ, ds=-cscsdζ代入式(25)，可得其标准形式为

(26)

根据Cauchy奇异积分方程理论，有

(27)

式(27)的等式右边前2项没有奇异项，因此可以省略。

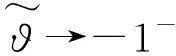
(28)

结合公式[9]

(29)

对式(28)进行无量纲化处理，有

(30)

通过对式(23)进行求解，得到ψ(1)和ψ(-1)，进而利用式(30)则可得到应力强度因子的数值解。

3 数值计算及讨论

压磁层和压电层材料分别为CoFe2O4和BaTiO3，其材料参数如表1所示。

表1 材料参数

3.1 核函数收敛性判别

3.2 参数分析

3.2.1 压电层厚度对SIF的影响

在不同压电层厚度下，讨论改变分布载荷作用位置θm对SIF大小以及SIF峰值点位置的影响，其变化曲线如图3所示，其中：几何参数r0=10 mm，r2=30 mm，α=72°，γ=48°，Δθ=θL-θR=24°。由图3可知：3种不同的载荷分布形式对SIF大小的影响关系为均布载荷>正弦型载荷>余弦型载荷；在其给定条件下，r1越大，即压电层越薄，SIF越大，且其变化量也越大；当且仅当θm=60°时，分布载荷范围与裂纹相重合，且裂纹θ=α与θ=γ的SIF相等，各自曲线对应的SIF峰值点关于θm=60°对称，此时该模型属于对称模型。因此，通过减小压电层的厚度，可在一定程度上削弱因模型不对称性而对SIF的影响。

3.2.2 分布载荷范围对SIF的影响

在不同分布载荷范围Δθ下，讨论改变分布载荷作用位置θm对SIF大小以及SIF峰值点位置的影响,其变化曲线如图4所示。由于裂纹θ=α与θ=γ关于θm=60°对称，因此仅以纹上尖端(θ=α)处得到的SIF的规律作图，其中r0=10 mm,r1=25 mm,r2=30 mm,(α+γ)/2=60°，裂纹对应中心角α-γ≡24° 。

由图4可以看出：SIF随Δθ的增大逐渐增大，且变化显著，但变化量却逐渐变小。上述结果说明：当Δθ较大时，裂纹尖端附近的载荷对SIF的影响较大，而其他位置的载荷对SIF的影响可忽略不计，这与文献[10]得出的结论(从集中载荷对裂纹尖端的影响来看，当集中载荷作用位置距离裂纹尖端一定范围内时才具有较为明显的影响)相一致。

4 结论

通过对3种不同分布载荷作用下的压电/压磁圆柱复合材料的断裂力学分析可知，压电层厚度以及分布载荷是影响材料中裂纹尖端的应力强度因子大小的主要因素，其中：压电层越薄，应力强度因子的数值越大；分布载荷位置的改变使得其中心角的角平分线与裂纹的角平分线不重合，即整个模型不具有对称性，因此应力强度因子并不是在裂纹尖端这一理想位置达到峰值。

上述结论可为此类复合材料的防断裂优化设计提供一定的理论参考。然而，Ⅲ型裂纹问题在实际应用中属于较为理想的工况，且材料外表面受力情况更复杂，因此相关问题仍需进一步研究。

参考文献：

[1] SPALDIN N A，FIEBIG M.The renaissance of magnetoelectric multiferroics[J].Science，2005，309：391-392.

[2] BAGHERI R，AYATOLLAHI M，MOUSAVI S M.Stress analysis of a functionally graded magneto-electro-elastic strip with multiple moving cracks[J].Math Mech Solid，2017，22：304-323.

[3] GUO Y K，LI Y D，Pan J W.Effects of complex modulus and residual stress on the vibration induced resonant fracture behavior of a multiferroic cylindrical structure[J].Engineering fracture mechanics，2017，171(1)：98-109.

[4] ZHOU K，LI Y D，LIU S L.Effects of the volume fraction of piezoelectric particulates in the magneto-electro-elastic interfacial region on the fracture behavior of a laminate multiferroic plate[J].Acta mechanica，2017，228：1229-1248.

[5] HU K Q，CHEN Z T.Strip yield zone of a penny-shaped crack in a magnetoelectroelastic material under axisymmetric loadings[J].Acta mechanica，2016，227：2343-2360.

[6] GRYNEVYCH A A，LOBODA V V.An electroded electrically and magnetically charged interface crack in a piezoelectric/piezomagnetic biomaterial[J].Acta mechanica，2016，227：2861-2879.

[7] LI X Y，ZHENG R F，KANG G Z，et al.Closed-form field in an infinite space of transversely isotropic multiferroic composite medium with an elliptical or penny-shaped crack:3D exact analysis[J].Int J Solid Struct，2016，80：96-117.

[8] BUI T Q，HIROSE S，ZHANG C Z，et al.Extended isogeometric analysis for dynamic fracture in multiphase piezoelectric/piezomagnetic composites[J].Mech Mater，2016，97： 135-163.

[9] TIAN W X，ZHONG Z，LI Y C.Multilayered PM/PE composites with periodic interfacial cracks subject to in-plane loading[J].Smart Mater Struct，2016，25：15-29.

[10] ZHANG J,JIN Y,LI Y D.Concentrated force-induced fracture of a multiferroic composite cylinder[J].Acta mechanica,2018,229:1215-1228.