基于高斯混合模型的滚动轴承故障诊断

2018-06-18张雪峰马静关崴赵彦辉李晓宇

时代汽车 2018年12期

张雪峰马静关崴赵彦辉李晓宇

哈尔滨东安汽车发动机制造有限公司技术中心黑龙江省哈尔滨市 150060

1 高斯混合模型理论

高斯混合模型是一种概率统计模型，它是由至少两个的高斯密度函数，赋予不同的加权系数的线性组合函数。

从以上分析可以看出,造成双块式轨枕挡肩断裂的主要原因为：①脱模机基础不均匀沉降导致脱模次数增加；②脱模平台四角不平导致模具四角受力不均，从而轨枕两端脱模不同步；③四个气囊放气不同步导致轨枕两端脱模不同步；④压缩空气潮湿堵塞气阀导致轨枕脱模不同步；⑤混凝土配合比选用不合理；⑥养护温湿度控制不当影响混凝土养护质量。

高斯混合模型定义如下：

2018年3月，董明珠、魏银仓和卢春泉在北京见面，最终3人达成一致意见，并很快在3月25日召开银隆第一届董事会第八次会议，决定免去孙国华的董事长及总裁职务，决定由卢春泉出任公司董事长，格力出身的赖信华出任公司总裁。

交叉分析①由于交叉分析的表格数据占用过多的版面，因此以下分析中删掉了有关的表格内容。发现：年度游览为1次的消费，主要通过熟人介绍获得信息；而年度游览次数2次以上的游客，主要是通过网络获取信息。小长假期间，旅游宣传册是游客获取信息的主要渠道；黄金周期间，熟人介绍则是游客获取信息的主要渠道。游览目的则不影响游客的信息获取渠道。

为第k类的高斯分布密度函数，其中：

一些科学史学者从政治制度层面，把近代科学未能在中国产生的原因归之于封建制度的长期束缚，认为封建专制的官僚政治是“科学赖以繁荣的民主制度的死敌”。戴念祖先生指出，中国在近四五百年间科学不发达的原因，不是中华民族愚笨，而是专制的封建官僚统治扼杀了科学技术的发明创造。明代《天工开物》一书的作者宋应星曾慨叹道：“丐大业文人，弃掷案头，此书与功名进取，毫不相关也。”该书最终在“帝子王孙”、官僚遍布的时代失传了。[6]

——函数方程中的参数集；

kω——各个类别的加权系数。

图1与图2为二维与三维高斯函数模型混合示意图。

运用高斯混合模型对数据进行特征空间拟合时需先进行参数初始化，由于数据来源为振动信号数据，具有明显的非线性，会导致运用极大似然函数法进行参数估计时计算量很大并且效果不理想。相比之下，期望最大化算法（EM）具有不受数据完善性与测量手段的制约，并能够克服似然函数参数估计方式局限的缺点[1]。

(5) 在堆积体中，发现相对静水环境下沉积的细颗粒泥质夹层(见图3)和稳定流水形成的层带(见图4)，因此从这个角度看，九襄地区堆积物的形成经历了较为复杂的气候演化，致使冰川受气温上升所产生的融水，其水动力条件之间差异明显。

2 滚动轴承故障试验及数据特征提取

本文以滚动轴承为研究对象，利用滚动轴承试验机及人为设定的故障零件进行实验，获得实验数据，提取分析数据特征值[2]，建立基于高斯混合模型的故障特征空间。并运用基于重合度思想的故障模式识别理论，对工程实际的发生的故障进行先期诊断。

2.1 建立故障试验

根据训练数据在多维特征空间中建立各个故障模式的GMM模型，其分布形式与故障模式相关。那么滚动轴承的故障模式识别过程近似相当于在已知的特征空间中，寻找与待测数据所转化的高斯模型最相似的分布形式，通过计算高斯模型之间的重合度来表征两者之间的相似程度。

本文采用期望最大化算法进行模型参数估计，并进行初始化。

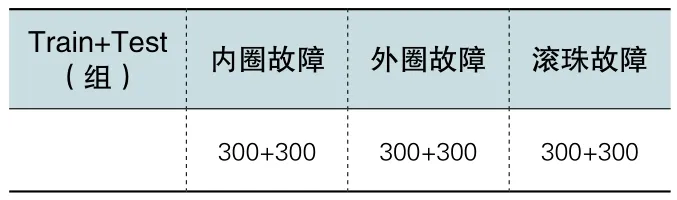
表1 实验数据分组情况表

2.2 实验数据特征提取与处理

在特征值选取时，分别在振动信号时域和频域方面选取具有能够表征信号内部信息的特征值，具体如图4所示。

按照上述识别思想，利用训练集数据，分别建立内圈、外圈和滚珠故障GMM空间模型，作为故障类型库。并利用测试集数据进行验证，计算测试集数据所建立的GMM特征空间相对于故障类型库中的每种故障模型的重合度（CV值）。

如图4所示，三条曲线分别代表内圈、外圈与滚动体故障在各个特征值方面的变化情况。

3 故障模式识别

3.1 故障模式识别方法及步骤

本试验在滚动轴承内圈、轴承外圈和轴承滚珠三个部位分别设置不同程度的故障故障模式，装于轴承试验装置，如图3所示，采集振动信号，并将数据分为两组，一组为训练组，训练高斯混合模型以及建立故障特征空间，另一组为验证组，对所建立的模型及特征空间进行验证，如表1所示。

定义离散形式的空间重合度，其表达式如式3-1所示：

式中：P1为根据训练集试验数据建立的高斯函数；P为根据测试集试验数据建立的高斯函数；为数据样本数；N为样本点；xi值即为待识别信号所属的GMM空间与已知GMM空间的重合度，CV值为0-1之间且为正反馈。具体流程如图5所示：

3.2 故障模式识别

国企面临的另一重大冲击来自乡镇企业。当时，乡镇企业在江苏南部和山东的胶东半岛迅速发展起来，乡镇企业因为机制灵活在竞争中明显优于国有企业，并出现了“星期天工程师”现象：国有企业的技术人员，星期天到附近乡镇企业“走穴”，进行技术支持。

识别结果如表2所示：

为了直观体现故障模式诊断的识别过程，对特征数据进行PCA降维处理，保留两主元并投影到二维空间中，如图6至图8所示：

表中数据表征使用待测样本数据所拟合出来的特征空间与故障类型库中各个故障模式的重合度，重合度（CV）最大者即为所诊断结果，与故障数据来源相符合。

从图6中可以看出，待测数据1特征分布位置与故障类型库中的内圈故障特征所分布的空间位置最近，以此诊断待测数据为内圈故障。

从图7中可以看出，待测数据2特征分布位置与故障类型库中的外圈故障特征所分布的空间位置最近，以此诊断待测数据为外圈故障。

从图8中可以看出，待测数据3特征分布位置与故障类型库中的滚珠故障特征所分布的空间位置最近，以此诊断待测数据为滚珠故障。

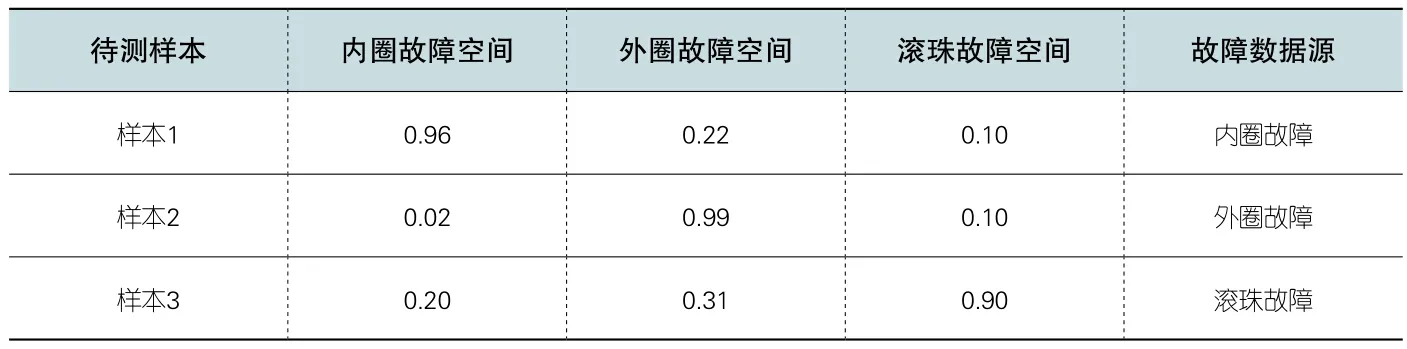
表2 待测样本识别结果

表3 待测样本识别结果

4 工程实际应用

结合国内某六速自动变速器在试验开发过程中所遇到的故障，运用本文理论进行故障模式识别。根据自动变速器在试验过程中所表征出来的差速器油封轻微漏油，且半轴跳动较大，初步怀疑差速器位置轴承磨损，结合试验过程中所监测的振动数据，根据本文所述进行特征提取，并建立基于高斯混合模型的特征空间，计算与已知故障模式库的重合度，如表3所示：

(3)投影分带方法。UTM投影和高斯投影一样为了减少投影变形进行分带处理。UTM投影将北纬84°至南纬80°之间按经度分为60个带，每带6°，从西经180°自西向东分带，两条标准经线距中央经线为180 km左右。高斯投影从0°经线开始，采用经差6°(或3°)自西向东分带。高斯投影的第1带是UTM投影的第31带。

经过对样机的实际拆解发现，差速器位置大轴承滚动体表面发生严重点蚀现象，如图9所示，牵连影响内圈与外圈的配合面，试验结果验证了理论的故障模式识别。