基于相似度数据融合的车辆航向角研究

闫晓雷，邵毅明，曾俊延

（重庆交通大学 交通运输学院，重庆 400074）

智能汽车技术已成为国内外众多汽车厂商的研发热点。其中，车辆操纵稳定性是智能汽车技术中的重要一环，需针对汽车行驶轨迹和姿态中的关键变量，如航向角和中心线偏移量进行实时反馈控制，实现电子稳定性控制，这些状态变量均可由传感器直接测量或通过控制算法取得。随着汽车市场竞争的加剧、传感器成本造价的降低、种类和数量的不断增多，为了提高整体数据精度和可靠性，多传感器数据融合显得尤为重要。

若已知传感器误差的先验概率分布和关联概率分布，则可利用最优统计决策法[1]，通过联合多传感器后验概率分布进行最优融合。当系统具有线性动力学模型和正态分布的系统噪声和测量噪声，则可以使用卡尔曼滤波[2]。本文的车辆航向角研究，先验知识是未知的，在该场景下的数据融合，消除数据融合算法依赖先验知识则是解决数据融合的重要环节[3-4]。

1 数据融合源

车辆航向角定义：车辆行驶方向与地球正北极的顺时针夹角。车辆航向角和横向位移偏差对车辆转向控制尤为重要；基于“预瞄-跟随”这一驾驶员模型，实时反馈控制车辆航向角和横向偏移量，可使车辆跟随任意复杂路径[5]。航向角也是计算车辆侧向加速度所必需的。

本研究采用车载VBox和司南高精度定位仪作为车辆附加传感器。其中，VBox的CAN数据接口与车辆CAN总线连接能够实时读取车辆数据。因此，一共有3个数据融合源，分别为VBox（数据采样间隔为0.01 s）、司南高精度定位仪（数据采样间隔为0.02 s）和车辆CAN总线数据（数据采样间隔为0.01 s），3个数据源实时采集车辆的行驶信息。VBox和司南高精度定位仪均基于卫星定位，在信号被遮挡时，由于锁定卫星数量不足，造成采集数据偏离正常值而形成噪点，数据融合前必须进行滤波预处理以去除噪声[6]。同时，数据采样间隔不一致，可将司南高精度定位数据进行线性插值，以实现相同采样间隔下的数据融合。节选10 s内的数据见表1。

表1 数据融合源（节选10 s的数据）

2 相似度数据融合算法

目前常用的数据融合方法多数需要先验知识的支撑，而对于大部分车辆行驶场景，先验知识是未知的，因此消除对于先验知识的依赖是首要前提。多传感器数据融合的同时也要考虑传感器测量数据的一致性和可靠性。基于相似度的数据融合算法，评估同质传感器测量结果之间的关联度，量化相似度和构建相似度矩阵，从相同时刻上测度一致性和在整个测量的时间序列上测度可靠性，对观测值进行加权[7]，从而得到最终的融合估计值。基于相似度的数据融合整体流程如图1所示。

图1 基于相似度的数据融合整体流程

2.1 相似度及构建相似度矩阵

设数据融合源集为（s1，s2，s3），其中s1，s2，s3分别表示司南高精度定位、VBox和CAN总线。Zi(k)表示k时刻数据融合源si的测量值（i=1, 2, 3），系统的状态方程无法得出时，可使用Zi(k)来计算相似度[4]。定义Sij为反映传感器测量值之间的相似度，表示传感器i和传感器j之间的相似性。Sij越大表示传感器i和j之间的相似性越强，反之则相似性越弱。相似度和相似度矩阵如式（1）和（2）所示。

式中：n为数据融合源头的个数n=3；Sk为k时刻构造的相似度矩阵，传感器与自身的相似度为1，且由于得出该矩阵为对称矩阵。

2.2 数据一致性测度

一致性测度表示传感器在k时刻时测量值之间的一致性。其公式为：

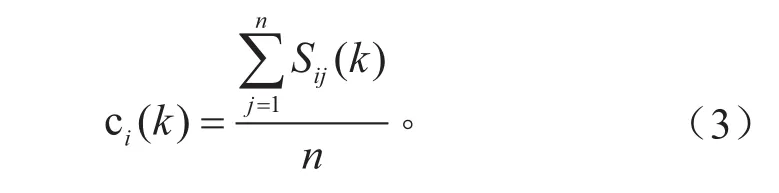
式（3）仅考虑了某一时刻的数据一致性，而在整个测量时间序列中，数据的一致性并不统一。因此，需要对其可靠性进行评估[8]，以便在整个测量过程中表现出很好的一致性。表示传感器i在时刻0至时刻k之间的一致性测度的时间序列，并引入一致性测度的平均值和方差评估传感器的可靠性[9]，如式（4）和式（5）所示。

对于一致性测度平均值E[ci(k)]}越大，方差(k)越小的传感器，其测量性能表现越稳定，因此，在接下来的数据融合过程中，可占据较大的权重。

2.3 分配权重及数据融合

设传感器i在k时刻的权重系数为wi(k)，由一致性测度的平均值E[ci(k)]}和方差(k)可知，wi(k)与E[ci(k)]}呈现正相关关系，wi(k)与σi2(k)呈负相关关系。同时，为避免wi(k)值非负，引入一个线性定义的映射关系，如式（6）所示。

式中：β为自定义系数，取值范围为0＜β≤1，其中，β的值越大，一致性测度的方差σi2(k)对权重系数的影响越大。在数据处理过程中发现方差一般小于0.01，为扩大方差的影响，β的值可取1。权重系数得到后，引入以下最终的数据融合公式：

式中：df(k)为k时刻传感器集测量数据融合后的最终值。

3 数据融合结果

融合数据源为：VBox测量数据、司南高精度定位仪数据和CAN总线数据。数据融合过程中缺乏目标真实值的先验知识，为此可引入一个整个时间序列的数据融合源平均值作为参考目标值。式（8）为引入的参考目标值。

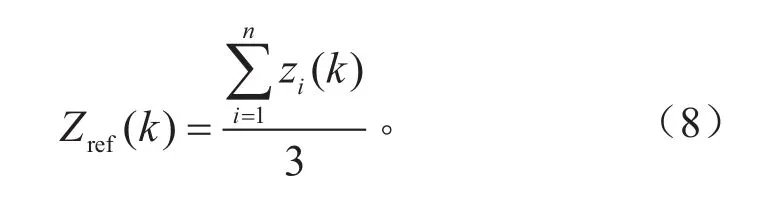
式中：Zref(k)为参考目标值；Zi(k)为传感器在k时刻的测量值。

司南高精度定位仪的航向角数据与参考目标值之间的对比和误差分析，如图2所示。由图2a可知，在10 s车辆行驶过程中，司南高精度定位仪的数据与参考目标值较为贴合，数据曲线反映数据逐步递增的趋势。由图2b可知，司南高精度定位仪的航向角最大误差值为0.784 2°，最小误差值为-0.276°，识别误差限在0.8°范围内。司南高精度定位仪基于GPS卫星天线和手机SIM卡运营商的基站定位，理论上的定位精度高于VBox单卫星天线定位（VBox支持Racelogic基站以进一步提高精度，但测试道路并无安装基站）。由图3～5的对比结果可知：司南高精度定位在锁定卫星数量满足要求时，测量精度最好。数据融合结果也符合司南高精度定位仪的精度优于CAN总线和VBox测量数据这一传感器特性。

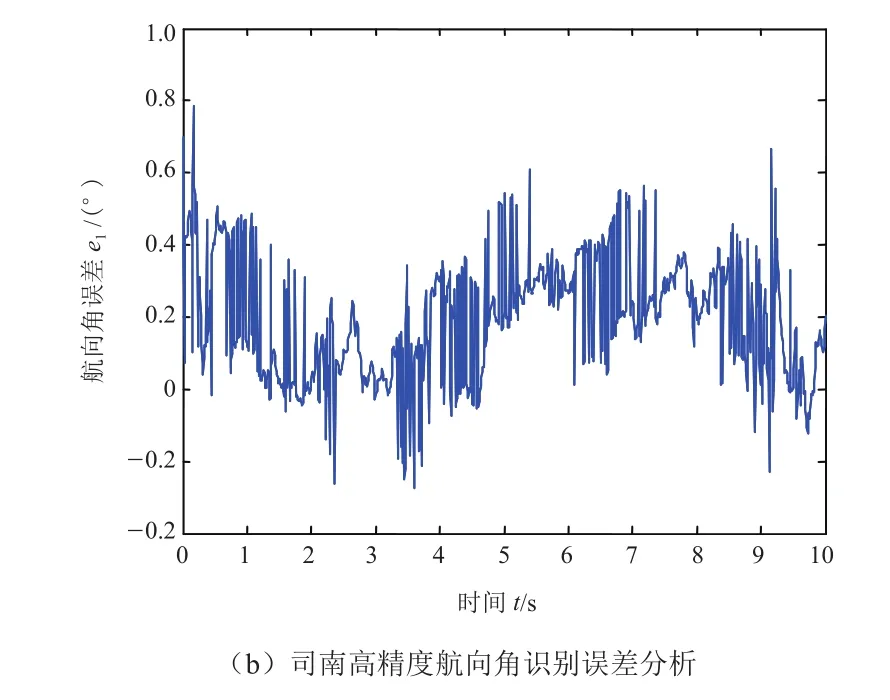
图2 司南高精度定位数据与参考目标值的关系

图3 VBox数据与参考目标值的关系

VBox数据与参考目标值之间的对比和误差分析如图3所示。由图3a可知，在10 s车辆行驶过程中，两种数据曲线均具有逐步递增的趋势。由图3b可知，VBox航向角的最大误差值为2.027 6°，最小误差值为0.486 5°，识别误差限在2.1°范围内。误差限大于司南高精度定位仪的识别时，可知测量精度低于后者。在计算该传感器的一致性测度方差时，小于司南高精度定位仪的一致性测度方差，说明VBox测量数据波动小，比司南高精度定位仪的测量性能更可靠，与传感器特性相符。

图4 CAN总线数据与参考目标值的关系

CAN总线数据与参考目标值之间的对比和误差分析如图4所示。由图4a可知，CAN总线测量数据虽具备逐步递增的特性，但测量精度不高。由图4b可知，CAN总线航向角的最大误差值为-0.539 4°，最小误差值为-2.696 4°，识别误差限在2.7°范围内。其中，识别误差限为上述3种传感器中的最大值，但该传感器的一致性测度方差一般处于三者最小的状态。综上所述，CAN总线测量数据虽然在三者之中的可靠性最好，但测量精度却最低。

数据融合最终值与参考目标值之间的对比和误差分析如图5所示。由图5a～d可知，在选取时间段内车辆行驶过程中，数据融合最终值与参考目标值紧密贴合；数据曲线反映数据逐步递增的趋势。由图5e可知，数据融合算法的航向角最大误差值为0.226 9°，最小误差值为0.012 4°；识别误差限在0.23°范围内。对比结果可知，误差限最小，数据融合算法精度明显高于3种数据融合源的识别精度。

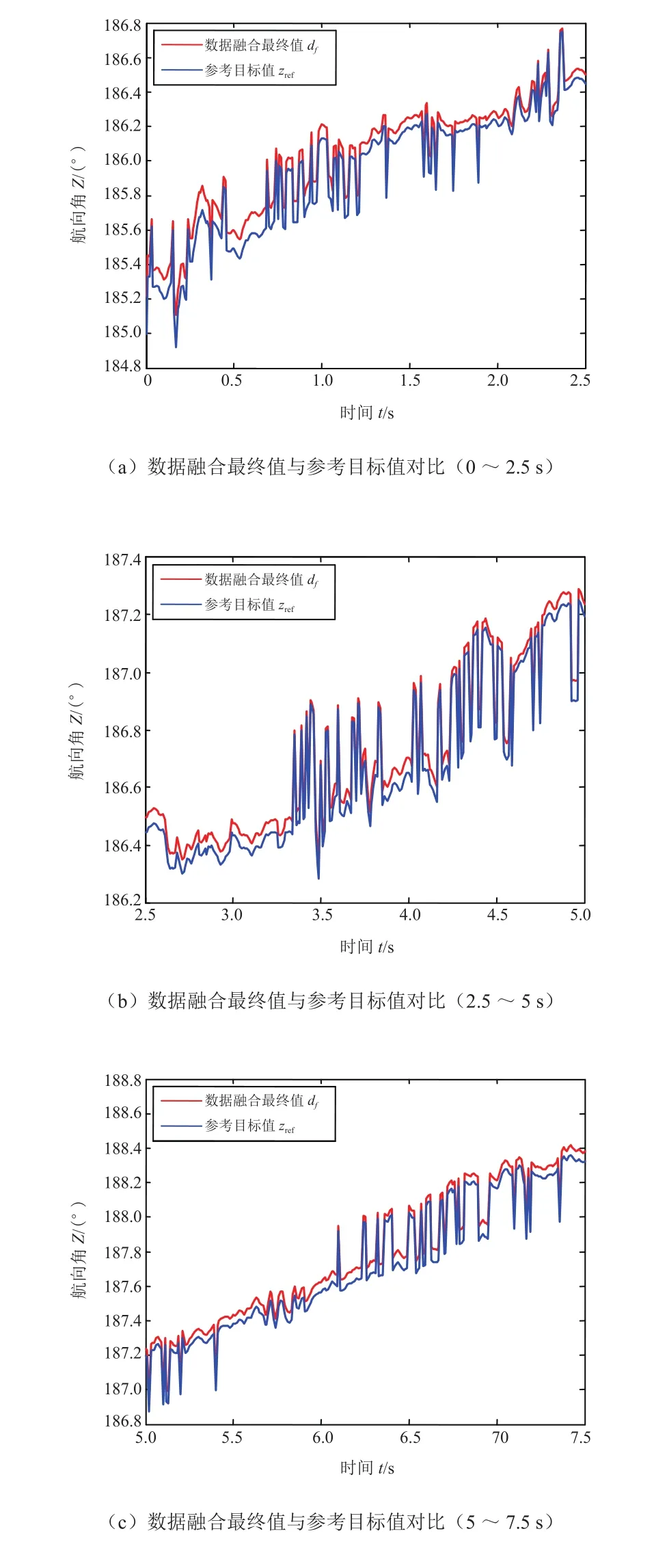
图5 数据融合最终值与参考目标值的关系

4 结论

本文将司南高精度定位仪、VBox和CAN总线作为车载传感器，三者测量数据中的航向角作为数据融合对象，包含指定时间序列信息的一致性测度作为融合的尺度，同时也将传感器自身的可靠性作为数据融合的权重，以此提高数据融合的整体精度。引入同一时刻传感器的测量平均值作为参考目标值，消除了数据融合过程中对先验知识的依赖。

在数据融合前，滤波预处理了因锁定卫星数量不足导致的数据噪点，但在实际操作过程中，传感器信号被遮挡后，一致性和可靠性降低，数据融合结果也变得不理想。数据融合对象需通过传感器测量值间接计算，应将测量值的误差传播扩散影响考虑在内[10]。

对比结果表明：数据融合最终值的误差限与3种传感器相比最低，性能效果和精度得到了明显的提高。构建相似度矩阵后，在计算一致性测度和可靠性的过程中，也侧面验证了司南高精度定位仪的测量数据精度高，但可靠性较差；VBox测量数据精度仅次于司南高精度定位仪，但可靠性优于后者；CAN总线测量数据精度最低，但可靠性较好。

[1] JOHN M R. Fusion of Multisensory Data [J]. The International Journal of Robotics Research，1988，7(6)：78-96.

[2] RAO B S Y，DURRANT-WHYTE H F，SHEEN J A .A Fully Decentralized Multi-sensory System for Tracking and Surveillance [J]. The International Journal of Robotics Research，1993，12(1)：20-44.

[3] 刘敏华，萧德云. 基于相似度的多传感器数据融合[J].控制与决策，2004，19(5)：534-537.LIU Minhua，XIAO Deyun. Multi-sensor Data Fusion Based on Similitude Degree [J]. Control and Decision，2004，19(5)：534-537. (in Chinese)

[4] 朴昌浩，禄盛，张艳，等.自动泊车系统设计[M].北京：科学出版社，2014：62-66.PIAO Changhao，LU Sheng，ZHANG Yan，et al. Automatic Parking System Design [M]. Beijing：Science Press，2014：62-66.(in Chinese)

[5] 陈焕明，郭孔辉.基于航向角和位置偏差控制的驾驶员模型[J].农业机械学报，2013，44(10)：36-40.CHEN Huanming，GUO Konghui. Driver Model Based on Heading Angel and Position Deviation Control [J].Transactions of the Chinese Society of Agricultural Machinery，2013，44(10)：36-40. (in Chinese)

[6] 罗俊海，王章静. 多源数据融合和传感器管理[M]. 北京：清华大学出版社，2015：21-23.LUO Junhai，WANG Zhangjing. Multi-sensor Data Fusion and Sensor Management [M]. Beijing：Tsinghua University Press，2015：21-23. (in Chinese)

[7] KOCH W. 跟踪和传感器数据融合[M]. 何佳洲，顾浩，蒲勇，等，译. 北京：科学出版社，2015：31-38 KOCH W. Tracking and Sensor Data Fusion [M]. HE Jiazhou，GU Hao，PU Yong，et al，Translate. Beijing：Science Press，2015：31-38.(in Chinese)

[8] APPRIOU A. 不确定性理论与多传感器数据融合 [M].郎为民，余亮群，陈 红，等，译. 北京：机械工业出版社，2016：4-8.APPRIOU A. Uncertainty Theories and Multi-sensor Data Fusion [M]. LANG Weimin，YU Liangqun，CHEN Hong，et al，Translate. Beijing：China Machine Press，2016：4-8.(in Chinese)

[9] 杨宝强，孙勇，徐明. 基于支持度的多传感器信息融合算法 [J]. 空军工程大学学报(自然科学版)，2007，8(2)：33-35.YANG Baoqiang，SUN Yong，XU Ming. Multi-sensor Information Fusion Algorithm Based on Support Degree[J]. Journal of Air Force Engineering University (Natural Science Edition)，2007，8(2)：33-35. (in Chinese)

[10] 费业泰. 误差理论与数据分析 [M]. 北京：机械工业出版社，2011：150-160.FEI Yetai. The Error Theory and Data Processing [M].Beijing：China Machine Press，2011：150-160. (in Chinese)