汽车试验场在场车辆总数趋势预测

曾 敬，向华荣

（重庆西部汽车试验场管理有限公司，重庆 408300）

随着汽车产业的发展，国内汽车试验场道路资源的需求越来越大。汽车试验场在场车辆总数为各试验道路车辆数及连接道路上车辆数的总和，依靠各道路道闸对进出车辆的统计可以获取在场车辆实时总数。了解车辆总数的变化及趋势可以为试验场管理者提供道路使用计划、运行调度、试验统筹、经营决策等方面的参考依据，可达到对日趋紧张的试验场道路资源充分利用的目的，并可为汽车试验场的数据可视化、智能化管理提供数据输入。试验场在场车辆总数经采样后可表示为典型的时间序列，其在一段时间内受各企业试验方案、场内安全调度管理影响，对突发天气情况、节假日等因素也有一定依赖，呈现出非线性与不可控性的特征。典型的汽车试验场由高速环道、耐久强化路、综合评价路等数十种特殊道路组成，每种道路属于一个有限空间内循环往复的交通流，其局部流动性具有一定的公共交通流的特点。对外开放的试验场，往往有数十个不同的试验主体单位，各主体单位又包含多个试验小队，各试验小队之间入场与出场的意图并未事先统一，所以在场车辆总数还呈现出一定经济模型的特征。目前国内外对试验场在场车辆总数数据的研究停留在历史统计方面，对该数据的深入分析及预测方面的研究较少，但对公共交通流量及经济模型的研究较多，韦凌翔等[1]、姚卫红等[2]、KUMAR等[3]、杨兆升等[4]对短时交通流采用支持向量机（Support Vector Machine，SVM）、人工鱼群算法、粒子群优化（Particle Swarm Optimization，PSO）、自回归积分滑动平均模型（Autoregressive Integrated Moving Average Model，ARIMA）等方法进行预测，达到了不错的短期预测效果，但对长时预测均未达到理想效果。程山英[5]用广义自回归条件异方差（Generalized Autoregressive Conditional Heteroskedasticity，GARCH）模型和ARIMA模型对股价波动趋势进行短期预测，在长时预测方面仍存在改进空间。张健等[6]用基于GM（1,1）[7]模型的BP算法对股票市场预测进行建模，通过对样本的训练，以寻求最优网络模型，表明了神经网络算法具有预测的潜能。文献[8]表明ARIMA及隐马尔科夫链（Hidden Markov Model，HMM）方法具有短期相关性，适用于短期预测，人工神经网络方法具有长期相关性，更适用于长期预测。本文先采用R软件的ARIMA方法及Facebook发布的Fbprophet方法对车辆数据进行简单分析及预测，然后使用LSTM及GRU方法对车辆数据进行训练，将部分保留数据作为测试数据进行测试，并用训练出的模型对未来1年在场车辆总数趋势进行了预测。

1 试验场场内车辆总量特点

某试验场3年以来的道闸管理系统数据库中车辆出入场数据多达700万条，初步梳理了该数据之后，对每天上午10时的在场总车辆数进行采样，得到共1 008组数据，在场车辆总数Yt可表示为离散时间序列[9]：

Yt总变化曲线如图1所示，该图反映出节假日期间，道路部分或全场封闭，车辆总数急剧下滑的特点。

图1 某试验场在场车辆总数Yt变化曲线

先采用ARIMA方法对在场车辆总数进行分析，对Yt进行1阶差分处理后，绘制ΔYt其自相关图和偏自相关图，发现自相关图有两个峰值然后截尾，偏自相关图第5阶后处于置信区间，暂判断Yt适用ARIMA（0,1,5）来进行拟合，该模型可写成：

式中：µ为常数；ui为白噪声；βi为各阶白噪声的系数，其拟合结果见表1。

表1 ARIMA（0, 1, 5）拟合结果

经分析，ARIMA（0,1,5）模型的赤池信息量（Akaike Information Criterion，AIC）为8 801.08，贝叶斯信息度量（Bayesian Information Criterion，BIC）为8 830.56，说明该模型复杂度过高，存在过拟合的现象，表明该模型不适合用于预测。

Fbprophet是Facebook 于2017年2月23日发布的一款开源数据预测工具，其基本模型为广义相加模型（Generalized Additive Models，GAM）的特例，可由式（3）～（6）表示。

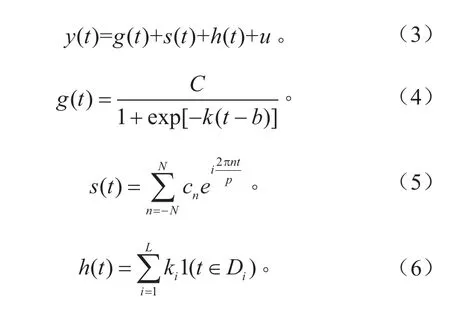
Fbprophet模型将时间序列分成4个部分的叠加，其中g(t)为增长函数，用来拟合非周期性变化，C为数据容量，k为增长率，b为偏移量参数。s(t)为使用傅里叶级数来表示的周期性变化；h(t)为假期、节日等特殊原因等造成的变化，Di为第i个虚设变量，可以将数据进行0，1设置，u为白噪声。

利用Fbprophet进行1年的预测，结果如图2所示。

图2 Fbprophet对Yt的拟合及预测曲线

通过Fbprophet能够对原始数据周期特性进行拟合，并可分离出总趋势、一周规律和一年规律，但对疏远点不能进行很好的识别。

2利用LSTM及GRU方法对在场车辆总数的变化趋势进行预测

2.1 LSTM及GRU方法介绍

LSTM是由Hochreiter和Schmidhuber于1997年提出的一种基于循环神经网络（Recurrent Neural Networks，RNN）上改进的机器学习神经网络[10-11]。相比于RNN，LSTM解决了梯度反传过程由于逐步缩减而产生的梯度消失问题，LSTM还可以识别并记忆时间序列中长期信息的特征，并对当前的输出产生影响，因此适用于处理和预测有疏远点特征的时间序列。

LSTM一个单位的基本结构如图3所示，其中xt序列为输入时间序列，ht为输出时间序列。LSTM的最大的特点就是输入xt不仅会影响到输出ht，还会将Ct-1改变为Ct，Ct和ht将输入到下一个基本单元甚至传递到更远的基本单元并影响其状态。

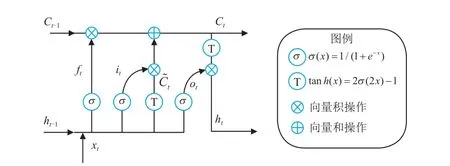
图3 LSTM单元结构图

LSTM 由输入层、输出层ht、遗忘层ft、状态更新层Ct组成，其间关系可由式（7）～（12）给出：

式中：Wi和bi分别代表各层的权重和偏置。

LSTM有多种变体，GRU[12]是LSTM的一种变体，它将遗忘层ft和输入层融合在一起，还将状态更新层Ct进行了隐藏，结构上比LSTM更为简单，其模型如图4所示。

图 4 GRU单元结构图

GRU满足如下关系：

式中：rt为遗忘层和输入层的融合，状态更新层隐藏后由zt和为输出层提供参数。

2.2 基于LSTM及GRU的在场车辆总数数据处理

本文基于谷歌发布的人工智能开源工具Tensor-Flow[13-14]建立LSTM及GRU模型，TensorFlow的特点是使用图 （graph） 来表示计算任务，图中的一个操作节点 （operation）称之为 op，一个操作节点获得0个或多个张量（Tensor）执行计算，生成 0个或多个张量，每个张量是一个类型化的多维数组。TensorFlow在被称之为会话 （Session） 的上下文中执行图，使用张量表示数据，通过变量（Variable）维护状态，使用feed和fetch操作输入和输出数据。TensorFlow还自带tensorboard可视化模块，可以清晰看到学习过程及模型结构。建立单层LSTM及GRU结构，横向并列布置100个LSTM，设置损失函数（loss）为均方损失[15]，利用优化器AdamOptimizer进行最小化loss优化并不断更新隐藏层的权重w和偏置b，对试验场内车辆总数Yt变化趋势的学习流程如图5所示。

图5 在场车辆总数机器学习流程

利用tensorboard可以看到LSTM和GRU的结构，如图6所示。

设置学习率为0.000 6，步长为60，总训练次数为5 000次，将在场车辆总数Yt的前715组数据作为训练数据进行训练。通过tensorboard可以看到整个学习过程中loss的变化（图7），两种方法的loss均能快速收敛。

图6 tensorboard中的LSTM和GRU单元结构

图7 LSTM和GRU方法进行训练的loss变化曲线

由表2可知，LSTM与GRU训练速度几乎相当，在loss对比上，除了在1 000步时GRU有超过LSTM的情况，其余时间的loss和最终loss，LSTM均超过GRU，通过5 000步的计算后LSTM的loss达到了0.019 11。

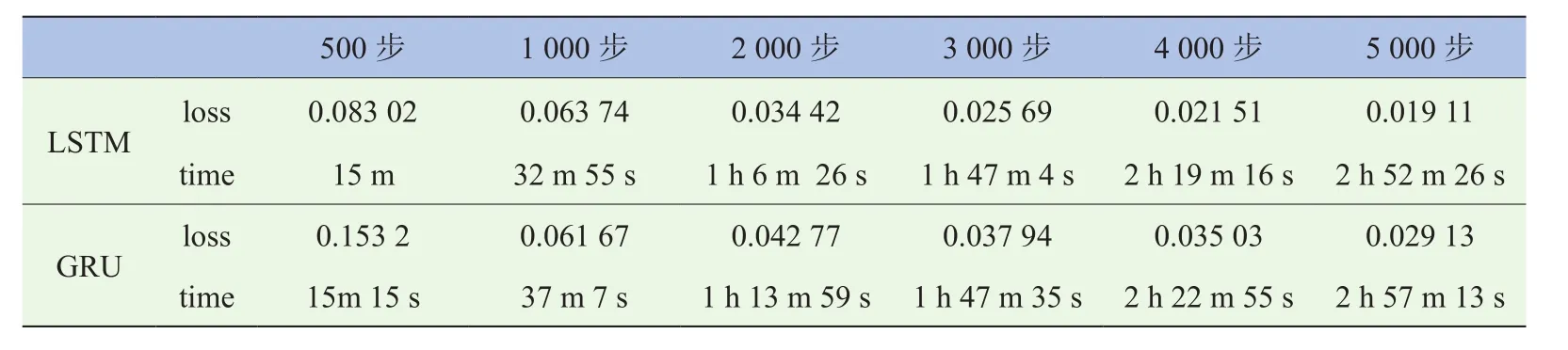
表2 训练过程中LSTM及GRU的loss对比

在训练过程中，LSTM和GRU权重w和偏置b的取值变化也可由图8和图9直观地表达。

图8 LSTM偏置bin，bout，权重win，wout的变化

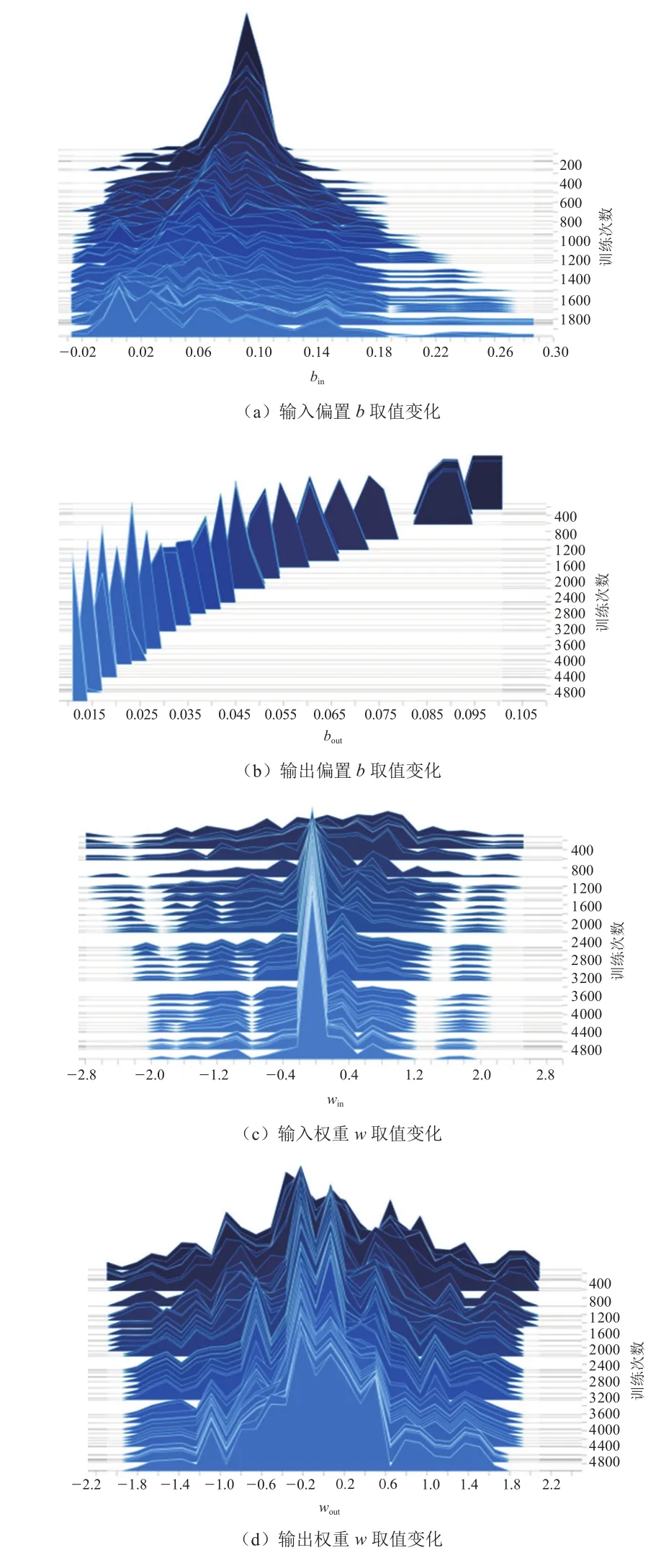
图9 GRU偏置bin，bout，权重win，wout的变化

可以看到在整个学习过程中，LSTM和GRU的权重w和偏置b的取值变化分布均匀，说明整个学习过程中没有出现异常，随着学习次数的增加，权重w和偏置b的取值变化相比学习开始之初的变化越来越趋于稳定。对应图7中loss的变化情况，可以看出随着学习次数的增加，loss的收益开始递减，到达3 000步左右时，已经达到一个学习“瓶颈”，loss的减少量已经非常细微。

使用训练好的模型进行293天的预测，并与Yt中的后293组数据进行对比测试，结果如图10所示。

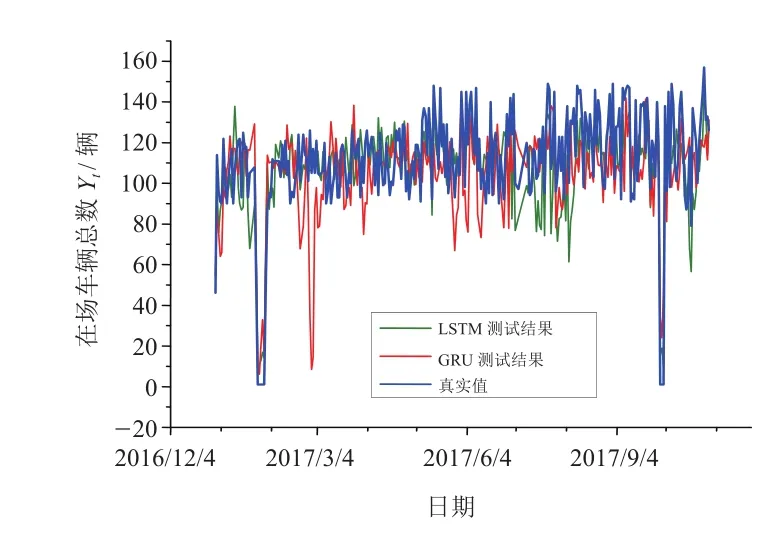
图10 LSTM方法与GRU方法的测试

测试结果表明，LSTM和GRU对原始数据疏远点均能较好地预测，根据实际情况，差异范围在30辆车内可以作为调度参考，LSTM和真实值总差异率为16.15%，GRU和真实值总差异率为25.76%，说明LSTM的预测效果更理想（表3）。

再利用Yt的1 008组数据分别进行LSTM和GRU方法的训练，并对未来1年场内车辆总数变化趋势进行预测，结果如图11所示。

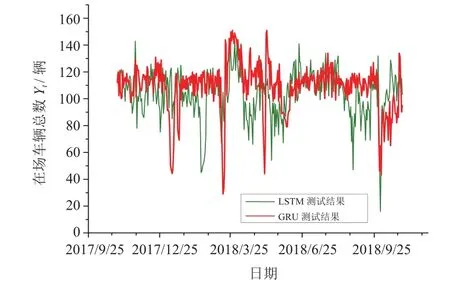
图11 LSTM方法与GRU方法对在场车辆总数Yt的预测

表3 LSTM及GRU预测值与真实值的对比

两种方法对节假日可能出现的封场、调度作了相应的预测，对春节后车辆数量的反弹现象均有一定判断。根据该预测结果，可在节后反弹时加强场内调度，适当增加道路容量以解决道路需求，在一些道路需求可能较少的节点，可以计划安排一些道路维护、道路检测等工作。

3 结论

本文对在场车辆总数Yt运用基于传统统计法的ARIMA和Fbprophet方法进行了分析及预测，发现效果并不理想。再利用TensorFlow建立LSTM及GRU模型，通过测试，发现两种模型均能对在场车辆总数的的周期特征、疏远点进行很好的识别，其中LSTM与真实值的差异值更小。LSTM及GRU均属于机器学习中的强化学习，学习过程主要在隐藏层上进行，整个学习过程中基于优化方式不断更新权重w和偏置b，并不能用一个直观的模型进行表示，但是可以看出机器学习方法比传统的基于具体统计模型的方法有更强的识别能力和预测能力，如何调整LSTM及GRU的参数，使差异值进一步降低可作为今后的课题。本文利用LSTM及GRU方法对未来1年场内车辆总数变化趋势进行了预测，该预测方式为试验场管理提供了一种新的统计方法，对试验场道路资源的计划调度提供了数据支持，值得进行进一步的研究与运用。

致 谢

本研究工作得到了“基于宽带移动互联网的智能汽车和智慧交通应用示范工程及产品工程化公共服务平台”重点项目的资助（项目招标编号为：0714-EMTC02-5593/20），特此致谢。

[1] 韦凌翔，陈红，王永岗，等.基于RVM和ARIMA的短时交通流量预测方法研究[J].武汉理工大学学报(交通科学与工程版)，2017，41(2)：349-354.WEI Lingxiang，CHEN Hong，WANG Yonggang，et al. Research on Short-term Traffic Flow Prediction Method Based on RVM and ARIMA [J]. Journal of Wuhan University of Technology (Traffic Science and Engineering)，2017，41(2)：349-354.(in Chinese)

[2] 姚卫红，方仁孝，张旭东. 基于混合人工鱼群优化SVR的交通流量预测[J]. 大连理工大学学报，2015，55(6)：632-637.YAO Weihong，FANG Renxiao，ZHANG Xudong.Traf fi c Flow Prediction Based on the Optimization of SVR of Mixed Artificial Fish Stocks [J]. Journal of Dalian University of Technology，2015，55(6)：632-637.(in Chinese)

[3] KUMAR S V，VANAJAKSHI L. Short-term Traf fi c Flow Prediction Using Seasonal ARIMA Model with Limited Input Data[J]. European Transport Research Review，2015，7(3)：9 Pages.

[4] 杨兆升，王媛，管青.基于支持向量机方法的短时交通流量预测方法[J].吉林大学学报(工学版)，2006，36(6)：881-884.YANG Zhaosheng，WANG Yuan，GUAN Qing.Forecasting Method of Short-term Traffic Flow Based on Support Vector Machine Method [J]. Journal of Jilin University (Engineering Edition)，2006，36(6)：881-884.(in Chinese)

[5] 程山英.基于模糊神经网络的短时交通流预测方法研究[J].计算机测量与控制，2017，25(8)：155-158.CHENG Shanying. Research on Prediction Method of Short-term Traf fi c Flow Based on Fuzzy Neural Network[J]. Computer Measurement and Control，2017，25(8)：155-158.(in Chinese)

[6] 张健，陈勇，夏罡，等.人工神经网络之股票预测[J].计算机工程，1997(2)：52-55.ZHANG Jian，CHEN Yong，XIA Gang，et al. Stock Prediction of Artificial Neural Networks [J]. Computer Engineering，1997(2)：52-55.(in Chinese)

[7] 刘思峰，曾波，刘解放，等. GM(1，1)模型的几种基本形式及其适用范围研究[J].系统工程与电子技术，2014，36(3)：501-508.LIU Sifeng，ZENG Bo，LIU Jiefang，et al. GM(1，1) Model of Several Basic Forms and Its Application Scope Research[J]. Systems Engineering and Electronics Technology，2014，36(3)：501-508.(in Chinese)

[8] 李永立，吴冲，王崑声. 优选时间序列数据模型的人工智能算法[J]. 计算机工程与设计，2011，32(12)：4190-4193，4201.LI Yongli，WU Chong，WANG Kunsheng. Artificial Intelligence Algorithm of Optimal Time Series Data Model[J]. Computer Engineering and Design，2011，32(12)：4190-4193，4201.(in Chinese)

[9] 原继东，王志海. 时间序列的表示与分类算法综述[J].计算机科学，2015，42(3)：1-7.YUAN Jidong，WANG Zhihai. The Expression of Time Series and Classi fi cation Algorithm [J]. Computer Science，2015，42(3)：1-7.(in Chinese)

[10] HOCHREITER S，SCHMIDHUBER J. Long Short-term Memory [J]. Neural Computation，1997，9(8)：1735-1780.

[11] GERS F A，SCHMIDHUBER J，CUMMINS F. Learning to Forget：Continual Prediction with LSTM[J]. Neural Computation，2000，12(10)：2451-2471.

[12] CHO K，VAN MERRIENBOER B，GULCEHRE C，et al. Learning Phrase Representations Using RNN Encoder-decoder for Statistical Machine Translation[C]//Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing(EMNLP)，Oct. 25-29，2014，Doha，Qatar.2014：1724-1734.

[13] ABADI M，BARHAM P，CHEN Jianmin，et al.Tensor-Flow：A System for Large-scale Machine Learning[C]//OSDI'16 Proceedings of the 12th USENIX Conference on Operating Systems Design and Implementation，Nov. 2-4，2016，Savannah，GA，USA.c2016：265-283.

[14] ABADI M，AGARWAL A，BARHAM P，et al.Tensorflow：Large-scale Machine Learning on Heterogeneous Distributed Systems[Z].arXiv：1603.04467v2 [cs.DC]，2016.

[15] 李航.统计学习方法[M]. 北京：清华大学出版社，2012：7-9.LI Hang.The Statistical Method of Learning [M].Beijing：Tsinghua University Press，2012：7-9.(in Chinese)