用于快速锁定全数字锁相环的反馈调节算法

谢琳琳， 王 扬， 乔树山， 黑 勇

(1. 中国科学院 微电子研究所 感知中心，北京 100029；2. 中国科学院大学，北京 100049)

频率调制是无线通信系统中重要的组成部分．基于小数锁相环的频率合成器通常用作本振，起到将基带信号搬移到载波频率上的作用．传统的锁相环主要由模拟器件实现: 压控振荡器产生振荡信号，作为输出信号的同时，分频后与参考时钟在鉴相器中比较相位，通过电荷泵输出误差电压，经过无源环路滤波器，控制压控振荡器，最终使相位差不再发生变化，达到锁定[1-3]．然而，压控振荡器、电荷泵、环路滤波器等模拟器件易受工艺、电压、温度的影响，易产生电容漏电、电流失配、动态范围有限等问题．同时，模拟器件通常占芯片面积大，难以在不同工艺间移植．相比于模拟锁相环，全数字锁相环采用数字器件或数字等效电路，所有模块输入输出均为数字信号，对外部噪声和环境变量并不敏感，也更加适应逐渐变小的工艺尺寸和电源电压．此外，数字电路可以使用自动计算机辅助设计软件，设计周期更短、易集成、可移植．

锁相环的锁定时间是一个重要的性能参数．在一些低功耗应用场景中，芯片在没有事件发生时需要进入休眠模式，锁相环也被关闭．当有事件发生，芯片被重新唤起发送数据时，环境变量很可能已经发生变化，原本保存的锁相环参数已经失效，此刻锁相环的锁定时间显得尤其重要．

锁定时间与锁相环采用的相位检测机制和环路滤波器带宽有关．全数字锁相环结构有多种，对应不同的相位检测机制．一种结构类似于传统的模拟锁相环，将其中的模拟器件替换为数字方式实现，由时数转换器、数控振荡器、数字环路滤波器和分频器等组成[4-5]．但它难以获得准确的整数相位差，极可能锁定在其他谐波处，且难以实现快速锁定．一种基于继电鉴相[6-7]的结构通过超前和滞后信号调节控制码，无法计算准确的小数相位差，锁定时间长．笔者采用另一种结构，它使用相位累加器替代分频器，配合时数转换器，该相位校准机制完全工作在数字域，可以随时获得当前的整数和小数相位差[8]．在该结构中，可以将校准过程划分为几个部分，在不同的过程中使用具有不同带宽的滤波器．笔者提出的反馈调节算法还可以在校准过程中根据实时相位差动态调节环路滤波器参数，实现自适应的可调环路滤波器，最终达到快速锁定的目的．同时全部电路均由软件根据代码自动生成，方便移植到不同工艺．

1 基于相位累加器和时数转换器的全数字锁相环

文中采用的全数字锁相环结构如图1所示．参考时钟fR来自外部晶振．数控振荡器输出高频可变时钟fV同时也是整个电路的输出信号．频率控制字定义为fV的理想频率与fR的比值．由于fR与fV完全异步，比较二者相位时易产生亚稳态问题，因此令频率高的fV采样fR，新产生的低频时钟fV，R与fV同步，作为全局时钟．相位累加器1在fV，R上升沿时累加频率控制字，估计参考时钟相位RR，相位累加器2累加fV的上升沿再被fV，R降采样同步，估计可变时钟相位RV．由于相位累加器的精度有限，需要使用时数转换器计算小数相位量化误差ε，定义为fR上升沿与下一fV上升沿之间的相位差．最终得到的总相位差φe，经过环路滤波器去除量化噪声后，控制Cc、Cf1、Cf2调节数控振荡器输出频率直至进入锁定状态．

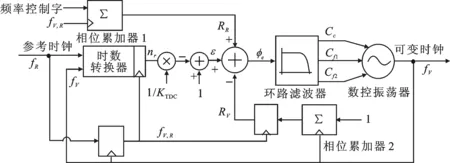
图1 基于相位累加器和时数转换器的全数字锁相环结构

具体实现过程中，数控振荡器作为全数字锁相环的核心部分，是实现数字-频率转换功能的基础．为了同时满足精度和频率范围的要求，数控振荡器整体采用折叠式环振结构[4， 9]．整个数控振荡器由三级组成，分别是粗调级、一级精调级和二级精调级．输入Cc、Cf1、Cf2，即可产生频率可调的方波信号．时数转换器用于测量小数相位量化误差ε．它采用简单的基于延时链的结构[10]，输出nr代表着fR上升沿与前一个fV上升沿的时间间隔Δtr等效的反相器延时的个数．定义图1中的归一化的时数转换增益KTDC=TV/TDINV，TV为fV的周期，TDINV为反相器的延时，则小数相位量化误差ε和总相位差φe可分别表示为

文中提出的快速锁定反馈调节算法作用于式(2)得到的总相位差φe，克服了传统锁相过程中环路滤波器结构单一、带宽固定的缺点，自适应地调节Cc、Cf1、Cf2，在实现锁相功能的同时缩短了锁定时间．

2 环路滤波器的类型介绍

根据阶数的不同，环路滤波器可大体分为Ⅰ型、Ⅱ型和高阶3种[10]．Ⅰ型滤波器如图2(a)所示，其中α为比例因子．使用Ⅰ型滤波器的全数字锁相环只有一个由数控振荡器产生的极点．它具有 -20 dB/dec 的噪声过滤特性，它的 -3 dB 带宽(fBW)为

fBW=αfR(2π) ．(3)

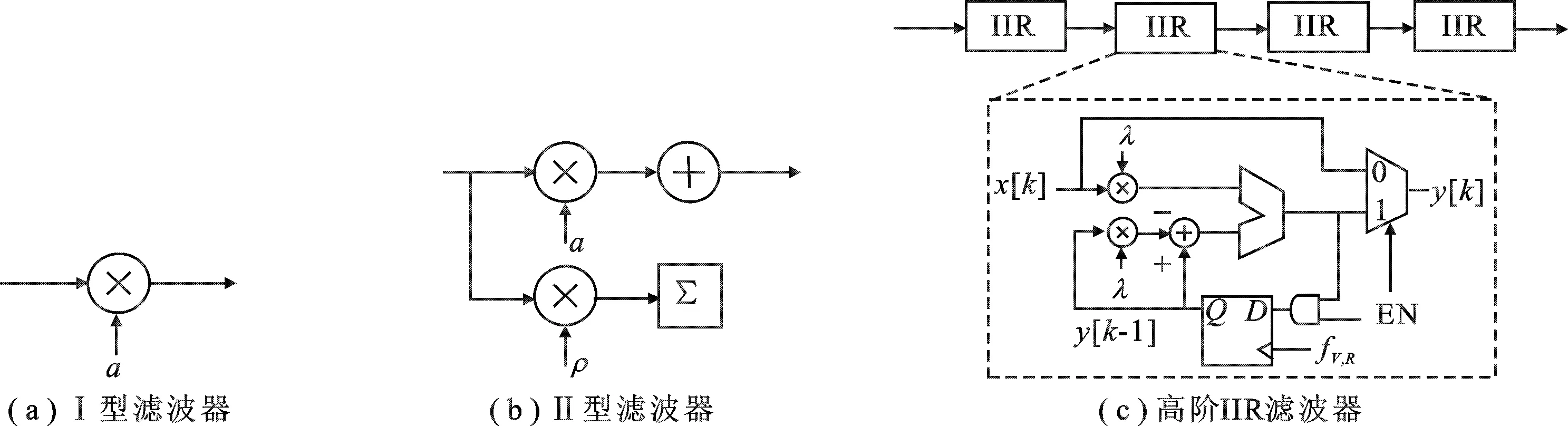
图2 滤波器结构

Ⅱ型滤波器增加一条积分支路，如图2(b)所示，ρ为积分环路增益，在零频处引入了第2个极点，得到 -40 dB/dec 的噪声性能．Ⅱ型锁相环的固有频率ωn和阻尼系数ζ分别为

高阶滤波器通常选择无限长单位脉冲响应(Infinite Impulse Response，IIR)滤波器，它比有限长单位脉冲响应(Finite Impulse Response，FIR)滤波器结构简单，滤波能力强．由于复杂的IIR结构稳定性差，因此设计级联的单极点滤波器，如图2(c)所示．使用高阶滤波器通常需要Ⅱ型滤波器提供零频处的极点，使用时将它们级联在一起．其中单级IIR滤波器的 -3 dB 带宽(fBW， iir1)为

fBW，iir1=λfR(2π) ．(6)

3 快速锁定调节算法

滤波器的阶数越高，带宽越窄，滤波性能越好，但锁定时间越长．传统的滤波器结构单一，需要在带宽和锁定时间折中．为了在获得同样滤波性能的同时实现快速锁定，设计过程中配合不同结构的环路滤波器，增加了结构和参数自适应特性，提出了反馈调节算法，如图3所示．根据数控振荡器的三级结构，分别寻找每级的最佳控制码，使输出频率逐步靠近目标频率．控制码Cc、Cf1、Cf2分为3部分：

其中，Mc、Mf1、Mf2为基准码，Tc、Tf1、Tf2为相对码，Tfrac为ΣΔ调制器输出的小数码，OV、OVf1、OVf2为 2 bit 有符号进位．初始时，Mc、Mf1、Mf2取预存值或中间值(数控振荡器每级可调范围Nc、Nf1、Nf2的一半)，使初始值到目标值的平均距离最短，其他码清零．定义归一化的频率差Δφe为相位差φe的差分值．定义归一化单位增益Δφc、Δφf1、Δφf2为Cc、Cf1、Cf2± 1时Δφe的变化量，在调节过程中实时修正．

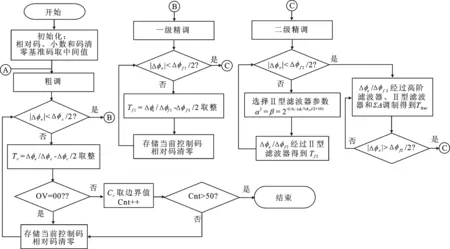
图3 快速锁定调节算法流程图

首先开始粗调，直接根据Δφe判断是否需要改变Cc: 当Δφe<Δφc/2，则证明粗调已锁定，否则直接计算需要调节的粗调相对码

Tc=[Δφe/Δφc-Δφc/2] ．(10)

如果Cc超出了可调范围0～Nc，取边界值，返回继续计算Tc，如果一直超出可调范围，则溢出标志OV一直为1，持续一定时间后判定无法锁定，停止计算．Cc改变后存储当前Cc为Mc，重新计算φe、Δφe和新的Tc、Cc直到无需改变，粗调锁定完成．

进入一级精调后，与粗调类似，判断是否锁定完成后，计算Tf1、Cf1，直到一级精调锁定完成．粗调与一级精调过程直接根据Δφe计算Tc、Tf1，可以在Δφe较大时实现快速锁定．相当于Ⅰ型滤波器且α=1，稳定性较差，但由于可以在后续对Cf2的调节过程中通过进位影响Cc、Cf1，实际上对Cc、Cf1和Δφc、Δφf1的准确度要求并不高，长期失锁时选取Cc、Cf1的平均值强制进入下一级．

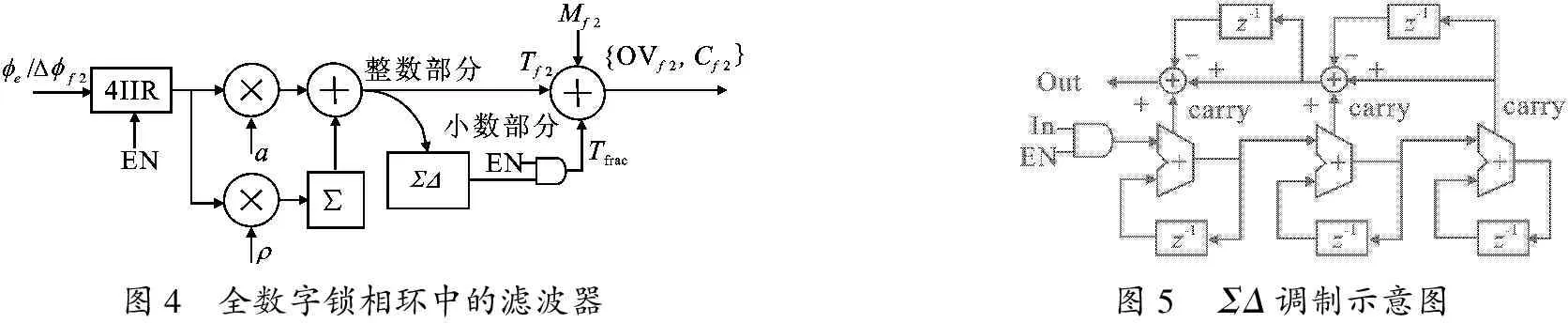
图4 全数字锁相环中的滤波器图5 ΣΔ调制示意图

当Δφe较小时，需要更高的准确度，二级精调的滤波器整体结构如图4所示．二级精调开始时，EN取0，只引入Ⅱ型滤波器，滤除噪声，减小带宽．设初始的 Δφe/ Δφf2=η0，调节过程中根据 Δφe/ Δφf2自适应选择滤波器参数：

α2=ρ=2-((η0-Δφe/Δφf2)/2+10)．(11)

如式(4)和式(5)，阻尼系数ζ固定为0.5，带宽受ρ影响．二级精调对φe/Δφf2而不是Δφe进行操作．φe/Δφf2经过Ⅱ型滤波器产生Tf2，无需反复存储Mf2、清零Tf2，更加稳定．当Cf2达到最优时，输出频率距离目标频率仍有一定量化误差．此时控制EN为1，启动高阶滤波和ΣΔ调制．ΣΔ调制的结构如图5所示，它将前面忽略的小数部分转化为高频的Tfrac，可以将带内量化噪声推向带外，被滤波器滤除．此时的相位差极小，加入高阶滤波器可以有效滤除有限的时数转换器精度、器件等引起的误差．

4 测试结果

整个全数字锁相环采用180 nm互补金属氧化物半导体(Complementary Metal Oxide Semiconductor，CMOS)工艺实现，除与功能无关仅为测试设计的输出驱动模块外，所有电路版图设计均通过数字后端自动完成，具有可移植性，芯片照片如图6(a)所示．整个芯片的有效面积为 0.9 μm2．测试时使用 1.8 V 电源电压，晶振产生 20 MHz 的参考时钟，单片机输入频率控制字．测试结果显示全数字锁相环的输出频率范围为 290～ 1 051 MHz．全数字锁相环输出最低频率时的功耗为 8 mW，当输出的频率增大时，数控振荡器、时数转换器和相位累加器2的工作频率增大，功耗也逐渐增加，最高为 17 mW．由于使用了环振结构的数控振荡器和基于延时链的时数转换器且自动生成版图，限制了全数字锁相环的噪声性能，因此整体的噪声性能一般，如图6(b)所示，低频时积分抖动较小，为 10.5 ps 左右，数控振荡器内的环振结构在高频时受上升下降时间影响，稳定性下降、性能变差，噪声偏大．

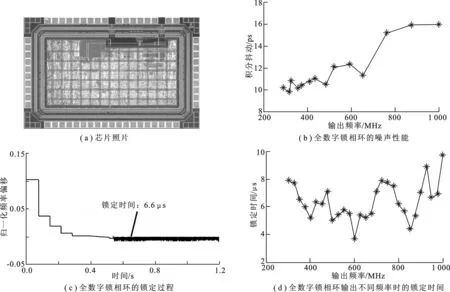
图6 芯片照片及测试结果

图6(c)举例说明了反馈调节算法的锁定过程，目标频率设为 425 MHz，初始频率偏移为10.75%时的锁定时间为 6.6 μs，相当于132个参考时钟周期．图6(d)汇总了输出不同频率时的锁定时间，由于测试时每一级数控振荡器的初始控制码均设为中间值，在每一级调节过程中，距离该级中间值越远，则该级锁定时间越长，因此总锁定时间呈现上下波动状．平均锁定时间为 6.4 μs，相当于128个参考时钟周期．最长锁定时间为 9.7 μs，相当于194个参考时钟周期．表1中对比了测试所得的各项性能．虽然受工艺和自动生成版图的影响，功耗和抖动性能一般，但文中提出的反馈调节算法使全数字锁相环的锁定时间明显缩短．

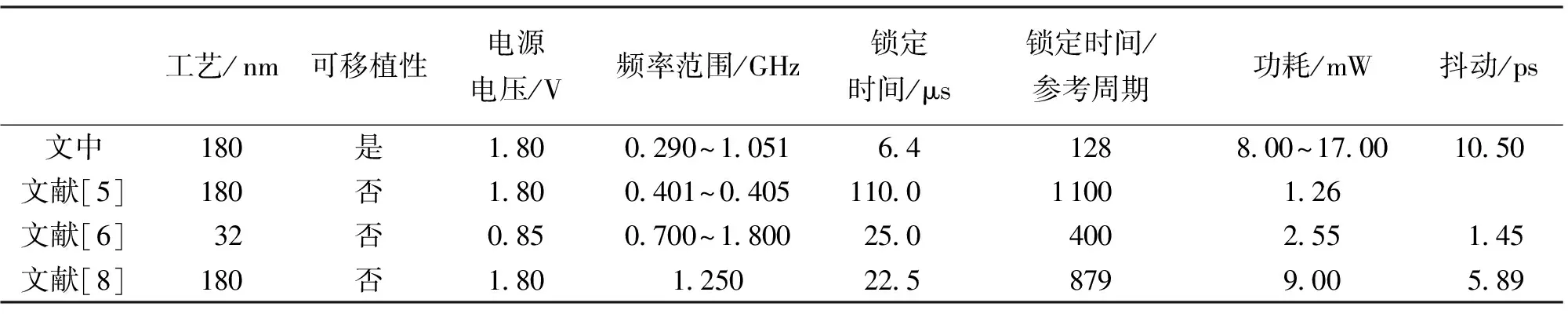
表1 测试结果对比

5 结 束 语

为了实现快速锁定的全数字锁相环，文中选择了基于相位累加器和时数转换器的电路结构，分析了3类传统滤波器的特性，克服了传统锁相过程中环路滤波器结构单一、带宽固定的缺点，增加了自适应特性，提出了滤波器类型和参数自适应的反馈调节算法．并在 180 nm CMOS工艺下设计实现了完整的全数字锁相环芯片，验证了该算法的可行性和有效性．

[1] 屈八一, 宋焕生, 周渭, 等. 一种新型不同频直接鉴相的锁相环[J]. 西安电子科技大学学报, 2014, 41(2): 172-177.

QU Bayi, SONG Huansheng, ZHOU Wei, et al. Novel Phase-locked Loop with Direct Phase Detection for Two Frequency different signals[J]. Journal of Xidian University, 2014, 41(2): 172-177.

[2] 梁亮, 朱樟明, 杨银堂. 应用于低压锁相环的高性能可编程电荷泵[J]. 西安电子科技大学学报, 2016, 43(2): 186-192.

LIANG Liang, ZHU Zhangming, YANG Yintang. High-performance Programmable Charge Pump for Low Voltage PLLs[J]. Journal of Xidian University, 2016, 43(2): 186-192.

[3] ALI E, HANGMANN C, HEDAYAT C, et al. Event Driven Modeling and Characterization of the Second Order Voltage Switched Charge Pump PLL[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2016, 63(3): 347-358.

[4] CHOI K H, SHIN J B, SIM J Y, et al. An Interpolating Digitally Controlled Oscillator for a Wide-range All-digital PLL[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2009, 56(9): 2055-2063.

[5] KHALIL W, SHASHIDHARAN S, COPANI T, et al. A 700 μA 405 MHz All-digital Fractional-N Frequency-locked Loop for ISM Band Applications[J]. IEEE Transactions on Microwave Theory and Techniques, 2011, 59(5): 1319-1326.

[6] HONG J P. A 0. 012 mm2and 2. 5 mW Bang-bang Digital PLL Using Pseudo Random Number Generator[J]. Analog Integrated Circuits and Signal Processing, 2016, 86(1): 39-50.

[7] BA A, LIU Y H, VAN DEN HEUVEL J, et al. A 1. 3 nJ/b IEEE 802. 11ah Fully-digital Polar Transmitter for IoT Applications[J]. IEEE Journal of Solid-State Circuits, 2016, 51(12): 3103-3113.

[8] HUNG C C, CHEN I F, LIU S I. A 1. 25 GHz Fast-locked All-digital Phase-locked Loop with Supply Noise Suppression[C]//Proceedings of the 2010 International Symposium on VLSI Design, Automation and Test. Piscataway: IEEE, 2010: 237-240.

[9] SHENG D, CHUNG C C, LAN J C, et al. Monotonic and Low-power Digitally Controlled Oscillator with Portability for SoC Applications[J]. Electronics Letters, 2012, 48(6): 321-323.

[10] STASZEWSKI R B, BALSARA P T. All-digital Frequency Synthesizer in Deep-submicron CMOS[M]. Hoboken: John Wiley & Sons, 2006: 109.