超高速飞行器气动外形对电波传播特性的影响

杨 鑫， 魏 兵， 尹伟科， 谭 畅

(1. 西安电子科技大学 物理与光电工程学院，陕西 西安 710071； 2. 西安电子科技大学 信息感知技术协同创新中心，陕西 西安 710071; 3. 陕西省等离子体物理与应用技术重点实验室，陕西 西安 710100)

当飞行器在大气层中以超高音速飞行时，其表面与大气激烈的相互作用将使周围气体电离，形成一层包裹飞行器的等离子体薄层，即等离子体鞘套[1-2]．等离子体鞘套在一定条件下会强烈干扰电波信号，甚至中断通信而威胁飞行安全，产生所谓的“黑障”现象．从20世纪60年代起，人们对鞘套中电波的传播特性进行了大量的研究[3-13]．但因等离子体鞘套电波传输特性的实验条件苛刻，前期往往采用理论分析和数值计算相结合的方法进行研究．数值方法在低频时常用时域有限差分(Finite Difference Time Domain，FDTD)方法，高频时可以采用射线跟踪算法．近年来，采用高频率的电磁波穿透鞘套实现无障碍通信，已成为克服黑障效应的可能技术之一．然而，鞘套中的电波传输特性与其电子浓度分布有关，而电子浓度分布又与飞行速度、高度、飞行器外形等均有关系．在现有文献对在不同飞行器外形条件下，鞘套中电波传输特性的研究并不多．鉴于此，笔者采用非均匀介质中的射线跟踪理论，研究了典型飞行目标(钝头和尖头)外部等离子体鞘套对高频电波的干扰特征．结果表明，尖头外形飞行器对应的外部鞘套流场的电子浓度量级较低，更有利于电波的传播．

1 典型飞行器外形及其流场分布特性

图1给出了钝头和尖头飞行器在高度65 km，速度为6 800 m/s时，流场中电子浓度的分布．为方便显示，图1(a)和图1(c)为取对数后的结果．由图可见，钝头等离子体鞘套中的电子浓度明显地高于尖头; 如图图1(b)和图1(d)所示，钝头鞘套的电子浓度在飞行器表面最大，随径向距离的增大而减小，随后上升到一个极大值，然后逐步减小为零．对于尖头鞘套，电子浓度的这种径向分布特性并不明显．

图1 典型飞行器外形及其流场中电子浓度分布

2 计算原理及数值方法

当飞行器以高频电波与外界通讯时，可采用几何光学方法对其传播特性进行近似分析．此时，电波在等离子体中的传播过程可由如下射线方程描述[14]:

(1)

其中，X=1-n2(n为媒质的折射率);p′表示电磁射线的积分路径;c为真空中电波速度;r、θ和φ为球坐标系的空间坐标值;kr、kθ和kφ为波矢量在球坐标系中分量．在不同方向上求解式(1)，就可获得电波在等离子中的传播轨迹，进一步便可得到电波的相关传播特性．

为了从式(1)中求解电波的传播轨迹，还需要知道等离子体的电磁特性．根据电波在等离子体中的传播理论[15]，传播参数可以下列方程计算:

(2)

其中，α为衰减系数，ε′和ε″为介电常数的实部和虚部，ne、ωp、v、ω、e、me和ε0分别为电子浓度、等离子体频率、等离子体碰撞频率、入射波频率、电子电量、电子质量和真空介电常数．结合式(1)和式(2)，式(3)给出了电波能量衰减量Att的计算方法[16]:

(3)

其中，E0为电波的初始振幅，E为观察点处的电场值．

计算鞘套中电磁射线轨迹时，需知任意计算点处介质参数．因测试(或仿真)数据通常以三维离散方式给出，为获得任意点的介质参数值，就需要通过已知参数点来计算．这一过程，文中采用高维Lagrange插值方法[17]来实现．电磁射线方程(1)的求解采用四阶Runge-Kutta法[17]．

3 结果及分析

3.1 钝头飞行器鞘套的传输特性

计算中，天线均以贴片式放置于飞行器前部 (如图1(a)); 工作频率取为 10 GHz、20 GHz 和 50 GHz; 飞行器的飞行高度为 65 km，速度分别为 6 120 m/s 、6 800 m/s、7 480 m/s 和 8 160 m/s; 满足下列条件之一时，射线跟踪终止:电波穿透鞘套;电场幅值E衰减至初始幅值E0的 1/10-5;电波频率小于等离子体频率．

图2表示天线频率为10 GHz时，不同发射角β(射线与飞行器轴线的夹角)情形对应的射线轨迹和衰减情况(衰减强度是观察点电场幅值比上初始电场幅值的百分比)．由图可见，当飞行器以较低速度飞行时，电波穿透能力强，能量传输率高，可达80%以上．但能量传输显示出一定方向特性．β越接近90°，能量传输率越高;越靠近飞行器表面，能量衰减越强．由于在 65 km 高处大气已变得稀薄，在相对低速的运动状态下，飞行器与大气的相互作用较弱，鞘套的电离程度较低以至于还无法对电波传播产生强烈的影响，所以能量传输效率较高；当射线发射角β接近90°时，由于穿透鞘套所需的路径较短，且轨迹的弯折效应较弱，所以能量传输率相对较高．

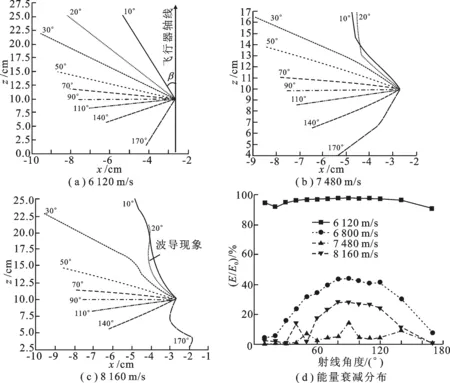
图2 不同速度和发射角度下的电磁轨迹及能量衰减

随着速度增加，图2显示电波轨迹出现明显的弯折．在靠近飞行器表面处甚至显现出波导的特性，形成电波在鞘套中传播而无法穿透鞘套的现象．这一现象可由图1(b)中鞘套的分布特性加以解释，图中以点A和B为分界点分为3个区域: 飞行器表面至电子浓度极小值点A为内层，点A至B为中间层，点B往外划为外层．射线传播过程中，若在到达分界点B之前就已折向鞘套内部，如图2(c)中20°发射角的射线，则形成波导现象; 若穿过点B，则其在外层的传播过程相当于由光疏介质向光密介质传播，因而将呈现往垂直于飞行器轴线方向偏折的趋势，如图2(c)以30°发射的射线．此时，电磁射线将穿透鞘套．

图3给出了频率为20 GHz时典型射线轨迹，以及20 GHz和50 GHz时的电波衰减特性．由图可见，电波传播特征与 10 GHz 时有相似之处的，例如能量传播的方向性及射线弯折等．但在提高频率的情形下，射线的直线性显著地增强，能量传输效率得到了有效的提升，比如当频率升高至 50 GHz 时，几乎50%以上的能量可穿透鞘套．

图3 不同飞行速度下电波传播及电磁参数特性

观察图3中能量衰减与飞行速度的关系可见，当速度超过阈值vt后，比如 7 480 m/s 与 8 160 m/s，能量传输率与飞行速度的关系将与低速时的相反．这一现象可由图3(d)解释，它给出鞘套的电子密度与飞行速度的关系，并根据曲线的特征分为2个区域．在区域1内，随飞行器速度的增加，飞行器表面与大气的相互作用增强，电离效应随之升高，粒子含量亦升高，使得该区域衰减特性与飞行速度呈正相关．但当飞行速度超过临界速度vt后，电离效应与飞行速度则呈现与低速时相反的变化关系，所以电磁衰减特性将负相关于飞行速度．在区域2内，由于飞行器的速度已接近甚至超过第一宇宙速度，这时飞行器表面与大气存在极强的相互作用．在这种极端的环境下，气动加热的增强将使周围气体的密度急剧降低[18-19]，从而间接导致离子密度的下降．同时，其他研究显示出了类似的现象，例如文献[20]指出，当钝头飞行器的飞行速度由低速逐渐接近 7 480 m/s 时，鞘套中的电子浓度将趋于饱和．

图4 不同飞行速度下尖头鞘套中的电磁轨迹

3.2 尖头飞行器鞘套的传输特性

由图1(c)可见，在相同飞行条件下，由于尖头鞘套的电子密度远低于钝头情形，并且两者电子密度的空间分布形式也有显著的差别．因此，与钝头鞘套中的电波传播特性相比，尖头鞘套将更有利于电波的传播．为显示这一特性，图4给出了尖头鞘套中电磁射线的传播情况，计算参数设置为: 飞行高度为 65 km，电波频率为 10 GHz．由计算结果可见，尖头鞘套对电磁射线的影响较弱，直线特性良好．而通过对能量传输特性的分析，发现98%以上的能量均可穿透鞘层．可见，与相同飞行条件下的钝头飞行器相比，尖头外形更有利于电波的传播．

4 结 束 语

文中以钝头和尖头超高音速飞行器为目标，研究了飞行器外形对电波传播的影响特征．研究表明，钝头飞行器产生的鞘套对电波传播有着强烈的影响，显示出丰富的传播特性，比如强烈的能量衰减，严重时甚至出现“波导”现象．随着电波频率的升高，这些现象将逐渐减弱．而对于尖头飞行器，由于其外形利于流场的通过，鞘套中的等离子体分布与钝头飞行器有着明显的区别．因而，在相同的计算条件下，这些现象并未在尖头鞘套中显现．

综上所述，由于飞行器的气动外形强烈地影响着流场的特性及分布，所以对电磁信号的传输亦影响明显．其中，尖头气动外形更有利于电磁波的传输，而增加电磁波的频率，将有效地降低鞘套对波传播的干扰，提升其整体的传输效率．这些结果可进一步促进人们对高超音速鞘套电磁特性的理解，并为缓解飞行器在高超音速条件下的通信困难提供理论参考．

[1] 李江挺, 郭立新, 金莎莎, 等. 等离子体鞘套中的电波传播特性研究[J]. 电波科学学报, 2011, 26(3): 494-500.

LI Jiangting, GUO Lixin, JIN Shasha, et al. EM Wave Propagation Characteristic in Plasma Sheath[J]. Chinese Journal of Radio Science, 2011, 26(3): 494-500.

[2] KEIDAR M, KIM M, BOYD I D. Electromagnetic Reduction of Plasma Density During Atmospheric Reentry and Hypersonic Flights[J]. Journal of Spacecraft and Rockets, 2008, 45(3): 445-453.

[3] SCHARFMAN W E. The Use of Langmuir Probes to Determine the Electron Density Surrounding Re-entry Vehicles: NASA-CR-66108 [R]. Washington: NASA, 1965.

[4] WEAVER W L, BOWEN J T. Entry Trajectory, Entry Environment, and Analysis of Spacecraft Motion for the RAM C-3 Flight Experiment: NASA-TM-X-2562 [R]. Washington: NASA, 1972.

[5] PETRIN A B. On the Transmission of Microwaves through Plasma Layer[J]. IEEE Trasactions on Plasma Science, 2000, 28(3): 1000-1008.

[6] THOMA C, ROSE D V, MILLER C L, et al. Electromagnetic Wave Propagation through an Overdense Magnetized Collisional Plasma Layer[J]. Journal of Applied Physics, 2009, 106(4): 043301.

[7] KUNDRAPU M, LOVERICH J, BECKWITH K, et al. Modeling Radio Communication Blackout and Blackout Mitigation in Hypersonic Vehicles[J]. Journal of Spacecraft and Rockets, 2015, 52(3): 853-862.

[8] LIU Z W, BAO W M, LI X P, et al. Influence of Plasma Pressure Fluctuation on RF Wave Propagation[J]. Plasma Science and Technology, 2016, 18(2): 131-137.

[9] SONG W J, ZHANG H. Analysis of Electromagnetic Wave Propagation and Scattering Characteristics of Plasma Shealth via High Order ADE-ADI FDTD[J]. Journal of Electromagnetic Waves and Applications, 2016, 30(10): 1321-1333.

[10] MOUSAVI A, ESFANDIARI-KALEJAHI A, AKBARI-MOGHANJOUGHI M. Optical Properties of Nonextensive Inhomogeneous Plasma Sheath[J]. Physics of Plasmas, 2016, 23(7): 073511.

[11] STARKEY R P. Hypersonic Vehicle Telemetry Blackout Analysis[J]. Journal of Spacecraft and Rockets, 2015, 52(2): 426-438.

[12] 田媛, 韩一平, 牛化恒, 等. 弱电离高超声速流场对太赫兹波传播影响[J]. 红外与激光工程, 2015, 44(12): 3690-3695.

TIAN Yuan, HAN Yiping, NIU Huaheng, et al. Effects of Weakly Ionized Hypersonic Flow on Propagation of Terahertz Wave[J]. Infrared and Laser Engineering, 2015, 44(12): 3690-3695.

[13] PODDAR S, SHARMA D. Blackout Mitigation During Space Vehicle Re-entry[J]. Optik, 2015, 126(24): 5899-5902.

[14] JONES R M, STEPHENSON J J. A Versatile Three-dimensional Ray Tracing Computer Program for Radio Waves in the Ionosphere: OT Report 75-76 [R]. Washington: US Department of Commerce, 1975.

[15] 王蕊, 郭立新, 杨阁. 等离子体涂层椭球目标的电磁散射[J]. 西安电子科技大学学报, 2008, 35(5): 903-909.

WANG Rui, GUO Lixin, YANG Ge. Investigation on the Electromagnetic Scattering from the Spheroid Covered with the Plasma[J]. Journal of Xidian University, 2008, 35(5): 903-909.

[16] 袁忠才, 时家明. 高功率微波与等离子体相互作用理论和数值研究[J]. 物理学报, 2014, 63(9): 095202.

YUAN Zhongcai, SHI Jiaming. Theoretical and Numerical Studies on Interactions Between High-power Microwave and Plasma[J]. Acta Physica Sinica, 2014, 63(9): 095202.

[17] KINCAID D R, CHENEY E W. Numerical Analysis: Mathematics of Scientific Computing[M]. 3. Pacific Grove, California: Brooks Cole, 2001.

[18] RYBAK J P. Causes, Effects and Diagnostic Measurements of the Reentry Plasma Sheath: AD-0718428[R]. Fort Collins: Department of Electrical Engineering, Colorado State University, 1970.

[19] KUNDRAPU M, LOVERICH J, BECKWITH K, et al. Modeling Radio Communication Blackout and Blackout Mitigation in Hypersonic Vehicles[J]. Journal of Spacecraft and Rockets, 2015, 52(3): 853-862.

[20] LI J T, GUO L X. Research on Electromagnetic Scattering Characteristics of Reentry Vehicles and Blackout Forecast Model[J]. Journal of Electromagnetic Waves and Applications, 2012, 26(13): 1767-1778.