基于正交迭代的有监督的稀疏主成分分析
2018-06-14李因果夏利宇
王 蕾,李因果,夏利宇
(1.中国人民大学 a.应用统计科学研究中心,b.统计学院,北京 100872;2.江苏师范大学 商学院,江苏 徐州 221116)
一、引 言
主成分分析是经典的数据处理和降维的工具,在工程、生物以及社会科学等领域都有着十分广泛的应用。主成分分析旨在寻找原始变量的一系列线性组合,使得由主成分张成的子空间能够尽可能地刻画原始数据的变动情况。然而,在求解主成分的过程中并未考虑到响应变量Y的信息,使其有效性受到限制,正如Cox所言:“主成分是由自变量X的边际分布计算得来,我们没有理由认为主成分一定包含了跟Y有关的信息。”作为一种无监督的降维方法,通过直接分解自变量X的协方差矩阵得到的主成分,并不一定是所感兴趣的投影方向。在回归和分类问题中,如果能将原始变量投影到与响应变量有关的方向上去,则更可能得到较合理的结果,这也促使了一些有监督的主成分分析方法的出现。
Oman在给定Y的条件下对X(即X|Y)建立了逆回归模型,并认为在给定X的条件下对Y(即Y|X)的回归模型中系数向量应当被包含在或者靠近X前几个主成分张成的空间[1];Bair等在求解主成分之前,先用自变量与因变量的皮尔逊相关系数进行了变量筛选[2];Cook等提出了关于主成分的逆回归模型及主成分拟合回归[3-4];Barshan等用希尔伯特-施密特独立性准则度量主成分与因变量的相依性,旨在寻找一个使X与Y的相依程度最大化的主成分子空间[5];Fuentes等将稀疏偏最小二乘的思想引入时间序列数据的预测中,即对同时包含X和Y的矩阵进行特征根分解[6];Giovannelli等在宏观经济时间序列数据的预测问题中,考虑了用标准化的主成分与响应变量Y的相关性来选择保留的主成分[7]。
上述文献在估计主成分时结合了因变量的信息,但得到的每一个主成分都是所有原始变量的线性组合,而在自变量个数较多时则难以解释每一个主成分的意义,这也促使了一些稀疏主成分分析方法的出现。Zou等将求解主成分的问题转化为线性回归的最优化问题,并将最小绝对收缩和选择算子以及弹性网的罚函数引入目标函数中,使某些较小的载荷直接变为0[8];Johnstone等证明了一定条件下稀疏主成分估计具有一致性[9];Ma提出用迭代阈值法估计主成分子空间[10];Kawano等在Zou的研究基础上,在目标函数中加入了主成分回归的拟合误差项[11];Yi等提出联合稀疏主成分分析,放松了各主成分的正交限制,且在目标函数中直接对特征向量矩阵的稀疏性进行惩罚[12]。国内也有将稀疏主成分应用于实际数据分析的文献,如喻胜华[13]。
本文主要研究基于正交迭代的有监督稀疏主成分分析方法(SSPCA)。当前几个特征值相等或很接近时,分别求解单个主成分可能出现不可识别的问题,因此本文使用正交迭代方法求解由前几个特征向量张成的特征根空间。正交迭代是计算特征根空间的常用方法,Ma基于此算法提出了计算稀疏主成分的ITSPCA及DTSPCA,前者是在正交迭代过程中增加了阈值步(Thresholding Step),而后者选取了方差较大的一部分自变量计算主成分,再进行正交分解,可用DTSPCA的结果作为ITSPCA的初值。ITSPCA和DTSPCA都是无监督的方法,若用主成分作为新的自变量进行预测,则无法识别出方差很大却与Y无关的自变量。有监督的主成分方法主要有:BSPCA(Bair’s SPCA)、ESPCA(Elnaz Barshan’s SPCA)、FSPCA(Fuentes’s SPCA)、GSPCA(Giovannelli’s SPCA)等,但FSPCA和GSPCA主要针对时间序列数据,因此在第三部分数值模拟中不予比较。
本文使用正交迭代方法求解主成分子空间,并利用距离相关系数度量各自变量与因变量之间的相关性,将与Y的相关性较弱且方差较小的自变量对应的载荷变为0,以得到稀疏的特征向量空间。相比ITSPCA和DTSPCA,本文给出的SSPCA更倾向于留下与Y有较强相关性的自变量,其预测效果也得到极大提高;对于BSPCA和ESPCA,SSPCA更易于识别X与Y的非线性关系,且能得到更稀疏的结果,使主成分更易解释。
二、研究方法
(一)主成分逆回归模型
考虑以下逆回归模型:
X=μ+Γvy+σε
(1)
其中X为p维列自变量;μ为p维常数列向量;Γ为p×s实数矩阵,s Oman将主成分逆回归模型用于描述校准问题,如Y为某些量的精确值,通常难以获得或者需要耗费大量财力物力,而X为易得的近似测量结果,一般用X来推断Y即建立关于Y|X的向前回归模型,但近似测量结果往往也与精确值有关,即X的取值受到Y的影响,故在此类问题中同时建立关于X|Y的逆回归模型也十分合理。 Cook认为此逆回归模型可以应用于测量误差、图像识别、微阵列数据等领域,且在引理中阐述了逆回归模型的系数向量Γ是向前回归模型中的一个充分降维的方向,即Y|X与给定ΓX的条件下Y(即Y|ΓX)的分布相同[3]。此外,Γ列空间的极大似然估计恰为X的协差阵的前s个特征向量张成的空间。不难看出,在X与Y满足此逆回归模型的条件下,若使用ΓX代替原始自变量X来预测Y,在降维的同时还可以保持预测效果不变。但在实际应用中,收集到的变量中只有一小部分是与Y相关的,即高维问题中的稀疏性假设,因此若能在求解Γ时将那些没有预测能力的自变量对应的载荷变为0,则可以利用较少的变量得到较好的预测效果。 设有p×s的列满秩矩阵Z,p>s,存在p×s的列正交矩阵Q和s×s的上三角矩阵R,使得Z=QR为Z的轻正交分解。 给定p×p正定矩阵A、列相互正交的p×s矩阵Q0,则正交迭代按如下步骤产生正交矩阵序列{Qk}⊆p×s: 1.Zk=AQk-1 2.QkRk=Zk(轻正交分解) 且Qk的列空间会收敛到A的前s个特征向量张成的空间[14]367-368,即主成分子空间,其中Qk、Rk、Zk分别代表第k次迭代得到的矩阵Q、R、Z。 算法1输入:自变量样本协方差阵S;主成分子空间维度s;初始正交阵Q0及用Q0建模拟合Y的拟合误差r0;阈值函数η,临界值γ1j,γ2k,γ3k,j=1,2,…,s;稀疏容忍度Sparsity。 (1)从k=1开始做。 (8)r0=rk 算法2输入:自变量样本协方差阵S;临界值αn。 (1)选取自变量子集XB={Xi∶i∈B},B为与Y相关性大于临界值的自变量的下标集合,B={i∶ωi≥αn}。 考虑用模型(1)产生数据,令μ=0、σ=1、s=1,2,3;Γ为服从[-10,10]均匀分布的p×s维矩阵列空间的一组正交基;vy是由{exp(Y)、I(Y<0)、Y}构成的向量,即s=1时vy=exp(Y),s=2时vy={exp(Y),I(Y<0)},依此类推。Y和ε皆来自标准正态分布N(0,1)。设p=1 024,观测个数n=200,其中0.7n=140个观测为训练集,其余0.3n=60个观测为测试集。假定1 024个自变量中分别只有前m=5,10,20,30,40个自变量与Y相关,由上述模型(1)产生,其余变量为服从t(3)分布的假变量。在Bair的数值模拟中,仅有1%的自变量与Y相关,故本文m的设置是合理的。用五种方法得到的主成分代替原始自变量,与Y建立四次多项式回归模型。在固定m=20时,令n=120、160、200、240,随观测个数增加而研究观察模拟结果的变化情况。 重复模拟100次,并将本文提出的方法SSPCA与ITSPCA、DTSPCA、BSPCA、ESPCA从拟合误差、预测误差和特征向量稀疏程度三方面进行比较,其中拟合误差用训练集的残差平方和来衡量,预测误差用测试集的残差平方和来衡量,特征向量稀疏程度则是计算平均每个特征向量不为0的元素个数。BSPCA的临界值选取使用R包superpc中的相关函数,ITSPCA和DTSPCA的有关参数均按原文推荐的设定,算法2中αn取0.03,模拟结果见表1~4所示。 表1~4中数据均为100次模拟结果的中位数,可看出在不同的设定下SSPCA和BSPCA的拟合误差和预测误差都优于其他方法,且在SSPCA保留的自变量个数远小于BSPCA的情况下,其预测误差仍然小于BSPCA。由表1表2易见,随着s的增大,五种方法的拟合误差基本都在减小,然而只有SSPCA和BSPCA的预测误差也呈下降趋势,其余三种方法的预测误差大多有所增加。 因SSPCA与ITSPCA、DTSPCA皆为稀疏主成分方法,得到的特征子空间都比较稀疏,每个特征向量平均非零元素个数均在10~30之间。ESPCA的结果最不稀疏,主成分是全部原始变量的线性组合,保留了最多的信息,同时也保留了所有的假变量,因此其拟合和预测效果并不尽如人意。BSPCA在求解主成分之前利用皮尔逊相关系数进行了变量选择,使得特征向量具有一定的稀疏性,但相比较稀疏主成分方法,保留的自变量个数仍然较多。由表1~2知,尽管测试集的样本量小于训练集,BSPCA的预测误差大多大于拟合误差,说明BSPCA在本文设定下,可能存在过拟合的问题。 表1 n为200时不同m的拟合误差与预测误差表 表2 m为20时不同n的拟合误差与预测误差表 表3 n为200时不同m的特征向量稀疏程度表 表4 m为20时不同n的特征向量稀疏程度表 下面将SSPCA应用于体脂数据body fat的分析,body fat数据集来自http://lib.stat.cmu.edu/datasets/bodyfat,旨在利用年龄、体重、身高等基本数据估算人体去脂体重,数据共有252个观测、15个变量,其中前143个观测为训练集,其余为测试集。人体密度和体脂率有近似一一对应的关系,因此将人体密度这一变量去掉,同时还向数据中添加了1 011个服从t(3)分布的假变量,以体脂率为因变量,其余为自变量建立回归模型,体脂率的数据用百分数表示,变动范围在0~100之间,训练集体脂率的箱线图见图1,从图1中可以看到体脂率主要在5~40之间波动。将数值模拟中的五种方法应用于body fat数据集中,分别选取前1~6个主成分,建立二次多项式回归模型(结果见表5表6所示),易见在用前3~6个主成分建模时SSPCA都能达到较优的拟合误差与预测误差,在用前5个主成分建模时SSPCA的预测误差达到最小。再结合五种方法各特征向量平均保留的变量个数来看,SSPCA方法优于其他四种方法。 图1 训练集体脂率的箱线图 sSSPCAITSPCADTSPCABSPCAESPCA拟合误差预测误差拟合误差预测误差拟合误差预测误差拟合误差预测误差拟合误差预测误差15 808.84 003.65 826.84 017.45 831.04 023.35 807.74 031.68 673.17 622.524 635.83 511.64 613.33 507.24 618.43 516.94 587.53 468.28 620.87 133.732 676.22 440.74 134.13 332.04 109.33 324.34 073.93 303.88 610.27 132.342 572.22 368.74 052.13 260.34 093.73 296.34 037.53 289.78 531.17 242.752 485.42 266.62 758.22 498.32 831.72 504.22 812.92 742.68 441.77 165.062 426.12 286.12 692.92 563.32 770.92 566.32 719.62 844.28 089.27 764.1 表6 不同方法分析体脂数据的特征向量稀疏程度表 本文基于正交迭代和距离相关系数,提出一种有监督的稀疏主成分分析方法SSPCA。该方法考虑了自变量与因变量之间的相关性,并在迭代求解的过程中将一些与Y相关性很弱的自变量对应的系数变为0,使得所求的特征向量只保留预测能力较强的信息。相比ITSPCA、DTSPCA、BSPCA和ESPCA方法,SSPCA方法在数值模拟和实例分析中都表现出了显著的优势。 参考文献: [1] Oman S D.Random Calibration with Many Measurements:An Application of Stein Estimation[J].Technometrics,1991(2). [2] Bair E,Hastie T,Paul D,Tibshirani R.Prediction by Supervised Principal Components[J].Journal of the American Statistical Association,2006,101(473). [3] Cook R D.Fisher Lecture:Dimension Reduction in Regression[J].Statistical Science,2007,22(1). [4] Cook R D,Forzani L.Principal Fitted Components for Dimension Reduction in Regression[J].Statistical Science,2008(4). [5] Barshan E,Ghodsi A,Azimifar Z,Jahromi M Z.Supervised Principal Component Analysis:Visualization,Classification and Regression on Subspaces and Submanifolds[J].Pattern Recognition,2011,44(7). [6] Fuentes J,Poncela P,Rodríguez,J.Sparse Partial Least Squares in Time Series for Macroeconomic Forecasting[J].Journal of Applied Econometrics,2015,30(4). [7] Giovannelli A,Proietti T.On the Selection of Common Factors for Macroeconomic Forecasting[J].MPRA Paper,2015. [8] Zou H,Hastie T,Tibshirani R.Sparse Principal Component Analysis[J].Journal of Computational and Graphical Statistics,2006,15(2). [9] Johnstone I M,Lu A Y.On Consistency and Sparsity for Principal Components Analysis in High Dimensions[J].Journal of the American Statistical Association,2009,104(486). [10] Ma Z.Sparse Principal Component Analysis and Iterative Thresholding[J].The Annals of Statistics,2013,41(2). [11] Kawano S,Fujisawa H,Takada T.Sparse Principal Component Regression with Adaptive Loading[J].Computational Statistics and Data Analysis,2015,89(C). [12] Yi S,Lai Z,He Z,Cheung Y,Liu Y.Joint Sparse Principal Component Analysis[J].Pattern Recognition,2017,61. [13] 喻胜华.基于稳健稀疏主成分的经济增长影响因素分析[J].统计与信息论坛,2017,32(3). [14] Golub G H,Van Loan C F.Matrix Computation[M].Baltimore:Johns Hopkins University Press,2013. [15] Li R,Zhong W,Zhu L.Feature Screening Via Distance Correlation Learning[J].Journal of the American Statistical Association,2012,107(499).(二)正交迭代
(三)基于正交迭代的有监督的稀疏主成分分析


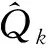
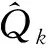

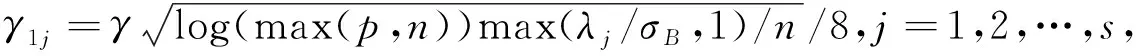

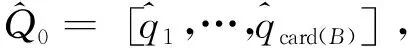
三、数值模拟




四、实例分析



五、结 论
