基于PMT技术的网络节能算法研究

赵 曦

(91550部队，辽宁 大连 116023)

互联网设备和业务的发展，不断丰富着人们的日常与社交生活，却也带来了能耗急剧升高的关键问题[1-2]。据统计和报道，互联网能耗占据了美国总能耗的2%～10%[3]。此外，互联网能源效率也极低，为互联网的可持续发展带来了挑战[4]。因此，如何有效减少互联网(IP网络)所需能耗受到了业界关注。

开放最短路径优先(OSPF)是IP网络中较为常见且使用频繁的域内路由协议。然而，由于业务流量的动态变化特性，OSPF利用链路权重优化流量分布的节能效果不佳[5-6]。此外，目前的文献对节能中业务量时间段的划分标准和方法不清晰，且业务量在各时间段切换的拓扑收敛更新时间会降低网络性能[7-8]。因此，以动态变化的流量为依据，对时间片段进行合理划分是非常重要的。

针对上述问题，本文基于预置多拓扑(PMT)技术设计了一种互联网节能(ESPMT)算法。该算法先以历史动态业务量为依据，对时间进行划分，并将各时间片中出现的流量峰值输入到该片段的节能问题中，从而得到流量最小的冗余和较好的节能效果。之后，利用邻域搜索设计快速启发式算法对链路权重进行优化，完成节能子拓扑的设计，从而实现链路容量约束下的单拓扑极限节能。

1 多拓扑的时间分割设计

本文基于历史记录中各时间段所表现出的流量特征对节能子拓扑进行设计，以实现业务流量动态变化下网络设备的工作和休眠调节。通常，IP网络流量曲线图在正常工作时会同时呈现波峰和波谷特征(带宽余量充足)。因此，在某个时间片范围内必定也会出现波峰值与供应量恰好相等的情形，划分的基准点便可选择该时间片下的波峰[9]。最终流量曲线图在波峰分割法下被划分为业务量需求上升和下降阶段，如图1所示。从图中可以看到，该曲线图按照波峰分割法可被划分为4个时间片。

图1 取波峰作为基准点的网络流量曲线图

2 节能子拓扑算法设计

由于OSPF协议下的路由，是以链路权重为依据通过最短路径计算而进行的。因此，在节能路由的相关设计中应休眠部分链路集合(利用率较低)，并转移业务流量到其他正常工作的链路[10-12]。由此可知，可以借助权重来调整网络中各链路上分布的业务流量。如下图2的网络拓扑(7条链路和5个节点，括号左右分别为权重及业务流量)所示。若节点a向e传送业务(6个单位)，则易知a-c-b-d-e以及a-b-d-e为该网络中的最短路径。此外，从图中也可以发现，链路权重越小(大)则流量越大(小)，优化链路权重可有效改变网络中的流量分布，进而完成节能的设计目标。

图2 拓扑权重及相应业务流量分布图

本文在权重优化的启发式算法上选用Fortz设计的邻域搜索算法，设定最大链路利用率的最小化为问题的优化目标，并调整权重搜索方法以实现负载和节能的均衡[13]。该算法具体为：

(1)权重向量及其他变量的初始化。其中，搜索面积q和次数z分别初始化为0；

(2)调整链路权重，产生新的权重向量；

(3)令z自加1，若z已累加至搜索次数，则跳转至步骤(8)；否则跳转至步骤(4)；

(4)利用最短路径算法计算网络中可能存在的最短路径链路(设定的业务工作节点之间)，从而获知流量分布情况及开关状态，并依照目标函数计算该权重向量作用下的能耗；

(5)评估能耗，若能满足链路容量约束，并能小于目前计算得到的最小能耗，则更新该最小能耗及最优权重向量，使q为0，跳转至步骤(7)；否则跳转至步骤(6)；

(6)令q自加1，若q已累加至搜索面积，则对权重向量实行扰动操作，并令z自加1，跳转至步骤(7)；否则，跳转至步骤(2)；

(7)判断搜索次数是否已经达到，若是则跳转至步骤(8)；否则跳转至步骤(2)；

(8)结束当前算法。

上述算法中的链路权重调整策略应使利用率较低(低于阈值Tlow)或较高(高于阈值Thigh)的链路上承担的工作业务尽量向利用率中等的相关链路转移，此时链路具有两级分布特性。因此，也具备较好的节能效果，并能满足一定的容量约束。本文取Tlow=0.90，Thigh=0.33，以消除网络拥塞并维持一定的网络性能。由于算法中的链路权重被初始化为1，增幅单位也为1。因此，链路权重的相应增减可具体为

(1)

其中，l，c和l/c分别代表的是链路负载、容量和利用率。

3 仿真及分析

结合仿真在多拓扑的时间片划分以及节能子拓扑两个方面对ESPMT算法进行性能验证，并与目前存在的其他算法进行对比及分析。

3.1 时间片划分对比和分析

本算法和等时间片划分方法在Matlab仿真中的冗余流量变化结果与对比，如图3所示。从图中可以看到，两种算法的预估流量均随时间片数目的不断增多而减少。在相同时间片数目下，ESPMT算法具有更小的冗余流量，与实际情况吻合较好。然而随着时间片数目的不断增加，ESPMT算法在冗余流量上的优势会不断变小，直至消失。

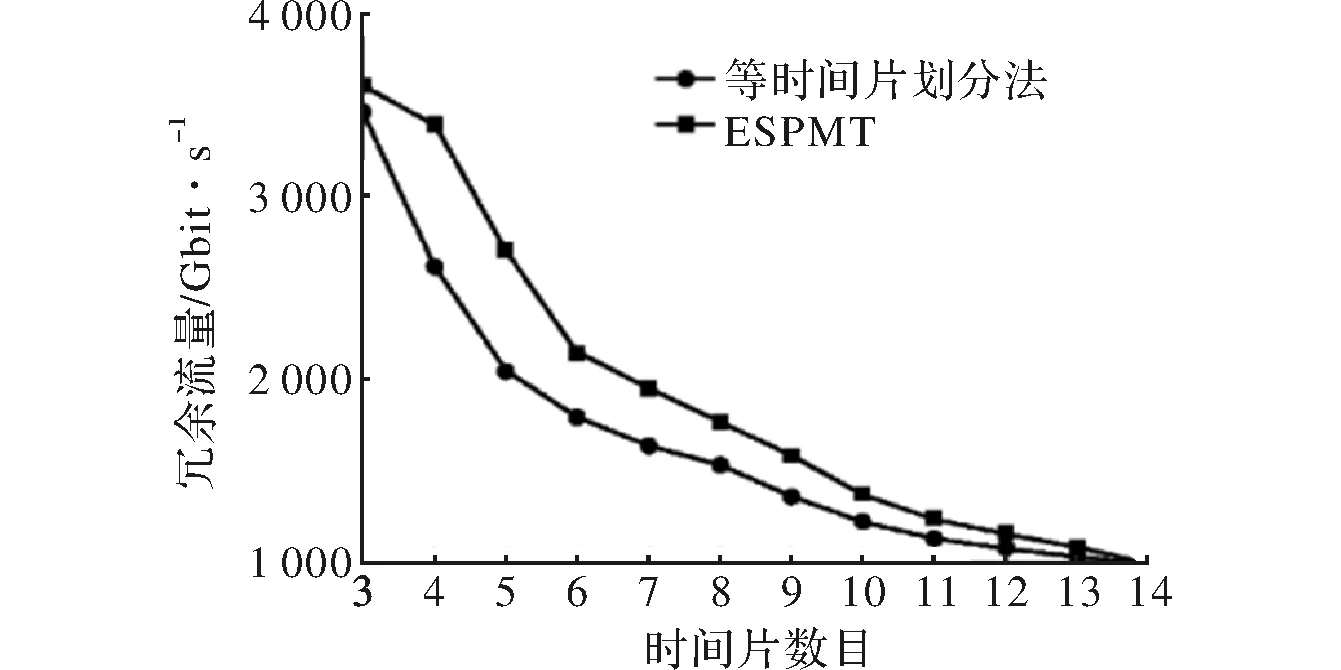
图3 本文算法和等时间片划分方法对比结果

3.2 节能子拓扑算法对比和分析

结合C++仿真，本文对ESPMT算法、基于代数连通度节能(ESACON)算法、最小流量(LF)算法和能量感知路由(EAR)算法的节能效果进行了分析和对比。该仿真拓扑网络分别为APARNET(32条链路和20个节点)和USANET网络(42条链路和24个节点)，各链路均为双向。此外，邻域扰动的权重在1～40范围内随机产生，搜索次数和面积分别为3 000和100，并取概率p为0.3以实现权重向量分量的改变。假设各链路由休眠转变为开启时具有相同的能耗，故目标函数可简化为工作链路总数的最小化。

本算法借助波峰将一天(5:00开始)划分成6个时间片(分别命名为1～6)，并针对各时间片的业务流量峰值进行对应的节能设计。各节能算法在两个网络下的能耗对比，如图4所示。从图中可知，ESPMT算法具有最优的节能效果；ESACON和EAR算法由于未曾对流量进行考虑，其能耗基本没有变化；而ESPMT和LF算法能耗与业务呈正相关。由此可知，ESPMT算法由于按照设定的流量矩阵，对网络的拓扑结构进行了确定，并借助权重调整产生了最优权重向量。最终趋使整个网络的流量向节能链路转移，因此具有良好的节能效果。

图4 各算法在不同网络中的拓扑能耗对比图

本文也针对不同的划分时间片方法(控制时间片个数为6个)，借助邻域搜索对各方法所耗的能量进行计算分析和对比。由图5可知，ESPMT算法对时间片划分的节能效果更优，且具有更低的能耗。总体来看，本文设计的算法能耗更低且节能效果更好，满足了设计目标和需求。

图5 不同时间片划分方法下邻域搜索的能耗对比

4 结束语

针对IP网络，本文基于预置多拓扑技术设计了一种节能ESPMT算法。该算法首先利用波峰分割法，对1天进行合理划分，得到若干个时间片；之后在各时间片中，利用邻域搜索(启发式)的相关节能方法和策略设计子拓扑算法。经仿真实验与测试，证明该算法和其他现有算法相比具有更优的节能效果，为相关网络节能算法的研究提供了参考。

[1] 张法,Antonio Fernandez Anta,王林,等.网络能耗系统模型及能效算法[J].计算机学报,2012,35(3):603-615.

[2] 李伟,张溪.半马尔科夫链的无线传感网络能耗模型的设计与分析[J].电子设计工程,2016,24(11):95-98.

[3] 伍元胜,郭兵,沈艳,等.面向核心网的多层网络能耗优化方法[J].计算机学报,2013,36(7):1538-1548.

[4] 陈晓华.高效节能虚拟网络映射模型与算法研究[D].上海:华东师范大学,2016.

[5] Cianfrani A,Eramo V,Listanti M,et al.An energy saving routing algorithm for a green ospf protocol[C]. Honolulu:INFOCOM IEEE Conference on Computer Communications Workshops,IEEE,2010.

[6] Cuomo W F, Abbagnale A, Cianfrani A, et al. Keeping the connectivity and saving the energy in the internet[C].Anchorage:Computer Communications Workshops,IEEE,2011.

[7] Chiaraviglio L,Mellia M,Neri F.Reducing power consumption in backbone networks[C].Seattle:IEEE International Conference on Communications,IEEE,2009.

[8] Jamakovic A,Uhlig S.On the relationship between the algebraic connectivity and graph’s robustness to node and link failures[C].Phoenix:Eurongi Conference on Next Generation Internet Networks,IEEE,2007.

[9] 王梦菊,吴小龙,石若玉.基于波峰搜索算法的视频客流计数系统研究[J].现代交通技术,2015,12(6):76-80.

[10] Moy J.OSPF version 2[M].Indianapolis:RFC Editor Press,1998.

[11] Guerin R A,Orda A,Williams D.QoS routing mechanisms and OSPF extensions[C].Detroit:Global Telecommunications Conference,IEEE,1999.

[12] Moy J.Multicast extensions to OSPF[M]. Indianapolis:RFC Editor Press,1994.

[13] Fortz B,Thorup M.Internet traffic engineering by optimizing OSPF weights[C].Vancouver:Proceedings of IEEE INFOCOM,2000.