基于不确定度理论的ECD不确定性定量表征方法
2018-06-13管志川胜亚楠
管志川, 胜亚楠
(中国石油大学(华东)石油工程学院,山东青岛 266580)
钻井循环时井底压力是影响钻井安全的重要参数,准确预测钻井循环时井底压力是保障钻井安全的前提[1-2]。目前,监测井底压力的方法有2种[3-5]。一是利用PWD仪器对井底压力进行实时的监测;二是根据钻井水力学模型预测井底压力。利用PWD对井底压力实时准确监测是最安全可靠的方法,PWD技术在国外已经比较成熟,多个国外油服公司都生产出了自己的PWD产品,并利用PWD监测井底压力取得了较好的效果;但是中国尚未研制出成熟的PWD产品,并且国外公司对该技术仍处于垄断阶段,致使用PWD服务费十分高昂;目前中国钻井作业大多数仍采用传统的水力学计算模型对井底压力进行预测。根据传统的钻井水力学计算模型得到的井底压力能够大致反映井下压力的变化趋势,但是由于其模型的精度以及计算模型中参数的随机性和模糊性等问题,使得准确预测井底压力的难度大,井底压力计算值与实际值之间存在误差,井底压力的预测结果存在一定的不确定性[6-7]。因此,需要对钻井循环时井底压力当量循环钻井液密度的预测结果进行不确定性分析。
1 ECD定量计算模型
井筒内钻井液液柱对井眼内产生的压力称作为井筒内静液柱压力(Pesd),通常用钻井液当量静态密度(ESD)表示,其表达式见式(1)[8]。钻井液当量循环密度(ECD)可以定义为ESD与钻井液流动造成的环空压降(∆Pf)之和,其表达式见式(2)[9]。

式中:Po为地面压力,MPa。
2 ECD不确定性分析
2.1 确定不确定度的理论方法
不确定性是广泛应用于管理学、数学、系统工程学领域内的概念,用于描述研究对象的随机性、模糊性和不可知性。不确定度是描述不确定性有效方法之一,分为直接测量和间接测量不确定度[10-15]。
2.1.1直接测量不确定度
直接测量不确定度又可分为A类不确定度和B类不确定度。
1)A类不确定度,用统计分析方法对参数进行评定,得到的标准不确定度称为A类不确定度分量,用符号uA表示,计算式见式(3)。
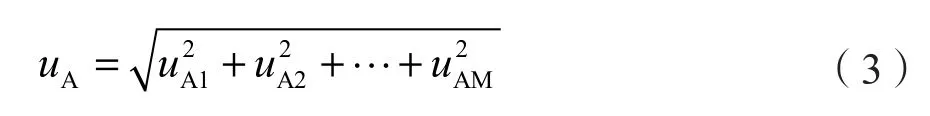
式中:uA1,uA2,...,uAM是M个不确定度分量。A类不确定度常用的计算方法是贝塞尔法,若只有一个分量,则A类不确定度计算式见式(4)。

式中:xi为第i次测量的结果;x为n次测量结果的均值;vi=xi-为残差。
2)B类不确定度。不用统计分析的方法对参数进行评定,得到的标准不确定度称为B类不确定度分量,用符号uB表示,计算式见式(5)。

式中:uB1,uB2,...,uBN是N个不确定度分量。
B类不确定度是根据工程经验或者相似情况下,同类参数的取值范围对待预测参数的不确定度进行评定的方法。假定工程经验得到的待预测参数误差分布范围为[-a,a],误差区间半宽为a,置信因子为t,则待预测参数的不确定度计算式见式(6)。

置信因子t的确定,需要首先假定测量值落在以[-a,a]为误差范围内的概率分布形式,然后查表确定;一般假定概率分布符合正态分布或均匀分布。
2.1.2间接测量不确定度
工程实际中,很多参数无法直接测量得到,需要经过一系列的计算求解过程才能得到。对于间接测量参数需要首先建立起与直接测量值之间的函数关系,然后通过直接测量参数的不确定度去估计间接参数的不确定度。假设x1,x2,…,xn是与间接测量量y相关的若干直接测量量,根据直接测量不确定度方法依次求得各个直接测量量的不确定度,然后构建间接测量量y与直接测量量{x1,x2,…,xn}之间的函数关系y=f(x1,x2,…,xn),最后根据测量不确定度评定指南(GUM),推导得到间接测量量y的不确定度评定公式,见式(7)。

间接测量不确定度具体分析步骤如下。①首先分析得到与间接测量量y不确定度相关的直接测量量{x1,x2,…,xn},确定直接测量量的均值和不确定度;并根据2者之间的函数关系,计算间接测量量的平均值;②计算间接测量量y的不确定度u(y);③最终得到含不确定度的间接测量量y的计算结果:y=±u(y)。
2.2 ECD不确定性的来源
参考不确定度评定指南(GUM)定义ECD的不确定度:ECD计算值不能确定的程度,表示计算结果分散性的大小;其值越小,说明ECD的计算值与井底真实值越接近,计算结果的可靠度也越高[15]。ECD的不确定性来源于计算模型的精度,模型中参数的随机性、模糊性等。
1)模型的精度。在构建ECD计算模型时,为了降低建立模型的复杂程度,会作出一些假设,如:计算钻井液静态密度时不考虑钻井液的热导率和比热随温度的变化、忽略热量经过钻柱、套管、水泥环及隔水管的内壁和外壁的热量损失、忽略井筒内钻柱偏心等;在计算环空压耗时,不考虑井眼清洁程度以及忽略钻井液在环空中不同深度的变化,认为钻井液密度在整个环空内保持不变等;这就不可避免地造成计算结果与实际值之间存在误差。
2)模型中参数的随机性和模糊性。ECD计算模型中有大量参数需要确定,如:计算钻井液静态密度时需要确定井身结构、钻具组合、工程设备、井场条件等基础数据、对流换热系数、无因次时间、海水和地层温度分布和热源项等参数;在计算环空压耗时需要确定井身结构、钻具组合、循环排量等参数。在模型参数中,一些参数在井下是模糊随机的,最为突出的是井径。大量的井径测井表明:井眼在井下是不规则的,井径分布具有随机性和模糊性。因此,基于这些随机不确定的参数得到的ECD计算结果也必然存在一定的不确定性。
2.3 ECD不确定度计算模型的推导
下面根据间接测量量不确定度求解方法对ECD不确定度计算模型进行推导。具体步骤如下。①首先定义ECD为间接测量量yecd,分析与ECD不确定度相关的直接测量量,并构建直接测量量集合{x1,x2,…,xn},然后根据直接测量不确定度方法确定各个直接测量量的均值和不确定度;并根据直接测量量的均值结合ECD计算模型,计算得到间接测量量ECD的均值;②利用全微分公式推导间接测量值不确定度的评定公式,计算ECD的不确定度;③最终得到含不确定度ECD计算结果。以幂律流体环空层流为例,推导ECD不确定度计算公式
幂律流体的流性指数和稠度系数计算如式(8),环空流速计算如式(9),雷诺数计算如式(10),摩阻系数计算如式(11),长度为L井段的摩阻损失计算如式(12),单位长度摩阻损失计算如式(13)。

由上式可以看出,循环压耗不确定性可以用直接测量量井径和循环排量的不确定性来表示。根据间接测量值不确定度的评定公式,可以得到单位长度环空压耗不确定度如式(15)和式(16)。

长度为L的井段环空压耗计算如式(17)。

长度为L的井段环空压耗不确定度计算如式(18)。
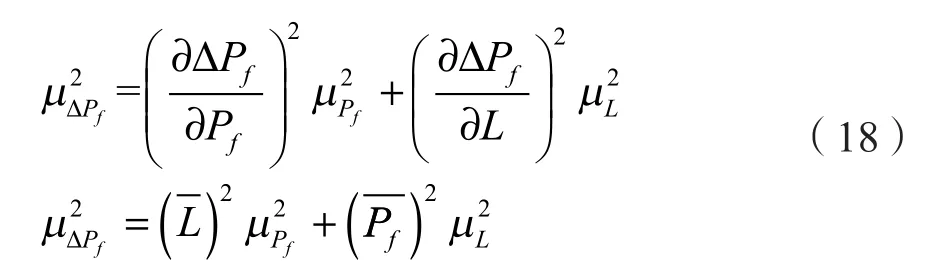
为了能够准确地计算井筒内的钻井液循环压耗,考虑到井筒中由于钻头尺寸、钻具结构及套管尺寸导致上下各部分的内外径不一致,采用分段求和处理的方法计算环空微元循环压耗的不确定度,然后求和得到整个环空井段循环压耗的不确定度。
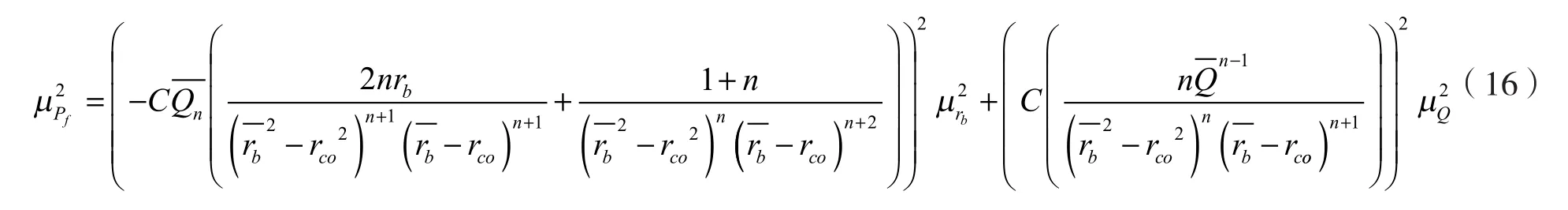
静态井底压力的不确定性可以用直接测量量静态钻井液密度和井深的不确定性来表示;根据间接测量值不确定度的评定公式,可以得到静态井底压力的不确定度计算如式(19)。
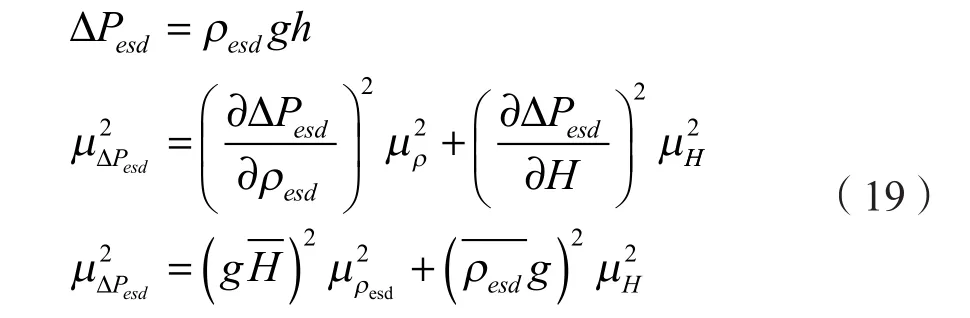
井底压力的不确定度计算如式(20)。

井底压力当量循环钻井液密度不确定度如下。

得到含不确定度的当量循环钻井液密度如下。

根据公式(21)、公式(22)可以看出,计算ECD的不确定度需要首先得到直接测量量井径、循环排量和静态钻井液密度的不确定度。
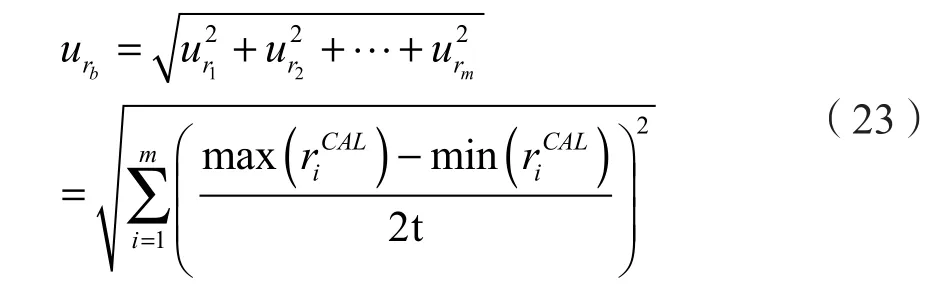
1)井径的不确定度。井径不确定度可以根据井径测井得到,忽略测井仪器误差,通过相同层位邻井的井径测井资料获得待钻井井眼的区间范围,即,则根据B类不确定度计算公式可以确定井径的不确定度如式(23)。
2)循环排量的不确定度。循环排量可以通过录井资料直接获得,循环排量的不确定度属于A类不确定度,根据A类不确定度计算公式,可以得到循环排量的不确定度计算如式(24)。

式中:n为循环排量监测数据个数。
3)静态钻井液密度的不确定度。根据上一小节可以计算得到随温度和压力变化的沿井深全井段的静态钻井液密度,选取一定井深范围内的静态钻井液密度为测量样本根据A类不确定度计算公式可以得到静态钻井液密度的不确定度计算如式(25)。
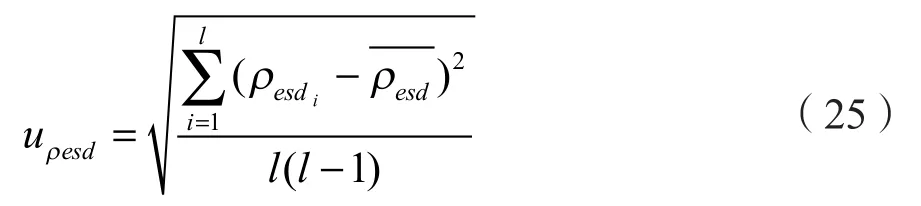
3 实例计算与结果分析
Madura BD气田位于印度尼西亚马杜拉(Madura)海峡,储层为礁灰岩,储层以上为大段泥岩、页岩、泥灰岩、薄层砂岩,地质环境复杂,钻进过程中频繁出现喷漏塌卡等工程风险问题,严重制约了钻井安全高效的进行。选取BD-1井进行实例计算与结果分析。BD-1井水深为26 m,井深为3 500 m,井底温度为180 ℃。从BD-1井钻前压力预测得知,井深1 500 m之前压力系数在1.0~1.2之间波动,属于正常静水压力体系;而从井深1 500 m以下,压力开始逐渐抬升。异常高压的存在严重影响了钻井的现场安全,因此应严格控制BD-1井钻进到该井深位置附近时井底循环钻井液密度,规避可能发生的井涌等井下工程风险。应用ECD不确定性分析方法,对BD-1井钻进到1 760 m处时的ECD不确定度进行计算与分析。BD-1井使用φ915 mm钻头钻至井深160 m,下入导管φ762 mm至井深155 m(MD/IVI),一开使用φ660.4 mm钻头钻至井深920.5 m,下入φ508 mm套管至井深916 m(MD/IVI);二开采用φ444.5钻头 mm钻至井深1 760 m(MD/IVI)。
3.1 井径的不确定度
为计算得到BD-1井井深916 m到1 760 m井径的不确定度,通过调研现场资料,选取BD-2井作为BD-1井的相邻井;结合BD-2井三开相同层位井径为φ444.5 mm井段的井径测井资料,根据公式(23)计算井径的不确定度;计算结果满足正态分布;正态分布的标准差即是BD-1井井深916 m到1 760 m井径的不确定度,其不确定度为8.18 mm,代入ECD不确定度计算公式。
3.2 循环排量的不确定度
循环排量的不确定度属于A类不确定度,通过BD-1井的录井资料直接可以得到循环排量的不确定度。结合BD-1井和BD-2井916 m到1 760 m的循环排量录井资料见图1和图2,根据公式(24)可以计算得到循环排量不确定度为0.18 L/s,代入ECD不确定度计算公式。

图1 BD-2井φ444.5 mm井段井径测井曲线
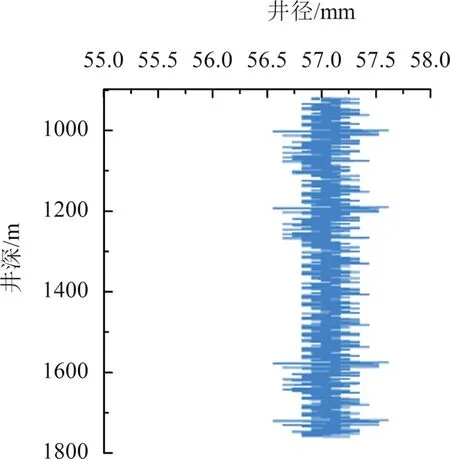
图2 BD-1井φ444.5 mm井段循环排量录井曲线
3.3 静态钻井液密度的不确定度
首先,根据2.1小节建立的高温高压条件下随温度和压力变化的钻井液当量静态密度(ESD)计算模型,求解得到ESD剖面见图3。根据A类不确定度计算公式可以得到静态钻井液密度的不确定度为:0.011 g/cm3,代入ECD不确定度计算公式。
最终,计算得到BD-1井钻进到1 760 m处含不确定度的ECD,用概率分布的形式表示,满足正态分布:N(1.315,0.0152),结果如图4所示。分析ECD概率分布及累计概率分布,如图5所示,可以获得累积概率为j1,j2(j1<j2)的ECD值 β1、β2,2个阈值构成了置信度为 |j1-j2|×100%的ECD区间,它表示该井深处ECD实际值落在置信度区间 [β1、β2]中的概率为 |j1-j2|×100%。在该实例分析中,ECD置信度为90%的区间为[1.284,1.340],也就是说ECD实际值落在该区间内的概率为90%。通过PWD实测获得井底ECD实际值为1.321 5,位于该区间内;而根据传统计算模型得到的ECD结果为1.284 5,与实际值之间存在较大误差。通过实例分析可知,提出的ECD不确定性定量描述方法,得到ECD是具有一定置信度的分布区间,不再是具体数值,这样更有利于工程技术人员把握深井复杂地层井底ECD的实际信息,为钻井方案的设计、优选和实施提供了科学依据。

图3 BD-1井钻进到1 760 m环空ESD分布示意图
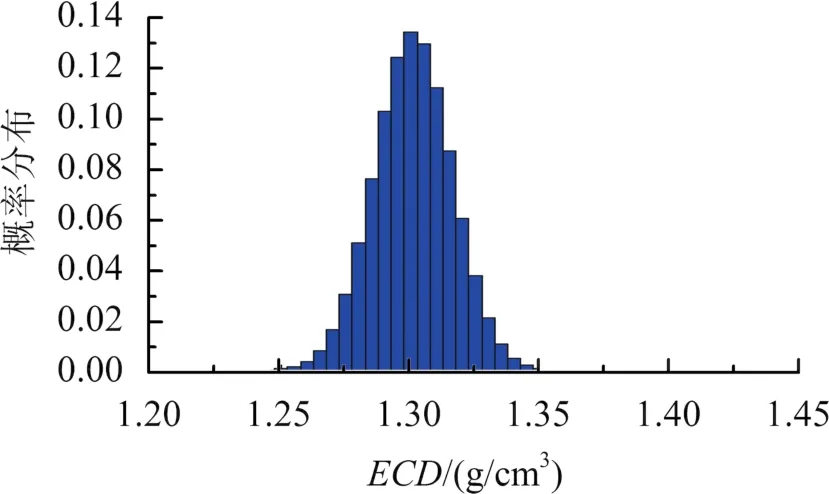
图4 BD-1井1 760 m处含不确定度的ECD分布
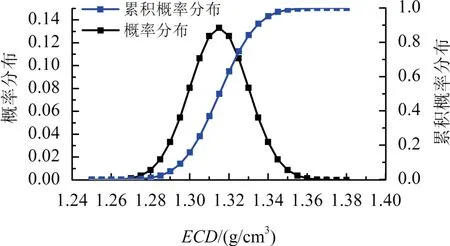
图5 BD-1井1 760 m处的ECD概率分布与累积概率分布
4 结论与建议
1.根据传统的钻井水力学计算模型得到的结果能够大致反映ECD的变化趋势,但是由于其模型的精度以及计算模型中参数的随机性和模糊性等问题,使得准确预测ECD的难度大,计算值与实际值之间存在误差,预测结果存在一定的不确定性。
2.在综合分析ECD定量计算模型的基础上,首先讨论了ECD不确定性的来源:ECD的不确定性来源于计算模型的精度,模型中参数的随机性、模糊性等。
3.基于不确定度理论,推导了ECD不确定度计算公式,并进行了实例分析。研究为ECD的科学描述提供了一种新思路,同时为保障钻井安全提供技术支持和科学依据。
