河网非恒定流计算方法研究进展

丁 雪

（扬州大学 水利与能源动力工程学院，江苏 扬州 225009）

1 引言

河网非恒定流的数值计算，是生产中经常要进行的工作，具有重要的实际应用价值，其计算问题可归结为一维圣维南方程组的求解问题。在目前的技术水平下，得到圣维南方程组的解析解比较困难，只能采用数值方法求解其近似解。用的较多的数值计算方法有特征线法、有限分析法、有限差分法和有限体积法。其中有限差分法又可以分为直接解法、分级解法、汊点分组解法、矩阵标识法、非线性方法以及汊点水位预测修正法。在有限差分法中，Preissmann隐式格式因为具有稳定性好、计算速度快的优点，所以得到了广泛应用。但是在河网非恒定流水力计算中，由于天然河道的形状不规则，而且河道之间的连接是交叉的，所以形成的系数矩阵是一个大型的、不规则、不对称的稀疏矩阵。当河网中汊点比较多的时候，矩阵运算会占用巨大的存储单元，同时由于大量的零元素参加运算，使得消元速度大为降低，计算次数猛增，计算时间较长，精度难以保证。因此河网非恒定流计算的核心问题是：如何压缩系数矩阵的尺度，减少对计算机内存的占用量。

文献[1]对平原河网水动力模型及求解方法进行过介绍。本文仅对有限差分法中的各解法基本思路进行讨论，比较其优缺点。

2 河网方程组的基本形式

2.1 微段方程基本形式

描述一维明渠非恒定流的Saint-Venant方程组是由连续与运动方程组构成：

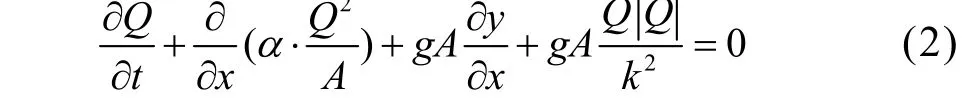
式中：A为过水断面面积；Q为流量；q为单位河长的旁侧入流量，入流为正，出流为负；y为水位；k为流量模数；α为动量校正系数；g为重力加速度；t为时间；x为沿水流方向的距离。

对于某一河段的任意两个相邻计算断面 i，i+1之间的微段，用Preissmann四点隐式差分格式差分逼近Saint-Venant方程组，可得微段差分方程组：

式中：Δy、ΔQ为待求水位、流量的增量；a，b，c，d，e 及， a′， b′， c′， d′， e′是已知水位、流量（包括迭代初值）的函数。

2.2 边点方程

边点方程形式是由边界控制条件决定的。边界控制条件有流量控制、水位控制、水位流量关系控制等多种情况[2]，但相应的控制方程可以统一用以下形式表示：

其中a、b、c为按实际条件导得的系数和右端项。这一类方程的非零系数最多只有两个，分别位于主对角线及紧邻该线（前或后）的位置上，排列也是比较规整的。

2.3 汊点连接方程

2.3.1 流量衔接条件

进出每一汊点的流量必须与该汊点内实际水量的增减率相平衡：

式中：n，m分别表示与某一汊点相连的河段数和汊点号，Vm表示m汊点蓄水量，在假设汇合区很小，水位变化引起的汇合区水体积的变化不计的情况下，可以简化成如下形式：

2.3.2 能量衔接条件

在汊点k的第i断面和第j断面间建立能量衔接方程时，如果考虑流速水头的影响和断面间能量损失，可以得到的方程(8)，其中， Z （ k, i） ，V（ k, i）分别表示k汊点第i断面水位和平均流速。

3 求解方法

在选择差分格式将圣维南方程组进行差分离散时，有显格式和隐格式两种不同的方法。显格式差分法的优点是容易理解，方便编制计算程序，但由于显式差分的稳定需要具备一定的条件，对计算时间步长要求苛刻，同时需要采取一定的技巧处理流量和水位之间的不协调性[3]，因而很少利用它来求解河网非恒定流。隐式差分法具有稳定性好，精度高的优点，但是在计算河网非恒定流时，如果使用隐式差分法，每进行一次迭代就要求解一个高阶代数方程组，使得隐格式的实际应用价值降低了。这篇文章中主要介绍隐格式的有限差分法，显格式方法可参考文献[4-5]。

隐格式差分法又可分为直接解法和分级解法两大类。

3.1 直接解法

直接解法的基本思想是把河道断面的水力要素作为基本未知量，去直接求解由内断面方程和边界方程构成的方程组。中山大学数学力学系从河网矩阵的特点出发，提出了“网河不恒定流隐式方程组的稀疏矩阵解法”，这种方法能够有效节省计算机内存，提高计算速度[6-7]。

由于直接解法系数矩阵阶数是河网中选取的计算断面数的两倍，所以对于大型河网，几乎是不可能用直接解法去进行求解。

3.2 分级解法

荷兰学者Dronkers首先提出了分级解法，在这之后又有许多学者对此法进行了进一步的完善。分级解法的基本思想[8]是先将未知水力要素集中到汊点上，待汊点未知数求出后，再将各河段当作单一河道进行求解。实践证明，分级解法与直接解法相比更能节约计算机存储量，更加实用。按照汊点上所保留未知数的个数对分级解法进行分类，如果在汊点上保留水位和流量两个未知数，称为二级解算法；仅保留水位或流量一个未知数，称为三级解算法。

3.2.1 二级解法

二级解法的基本思想是将所有的边界方程和河段方程构成的二级连接方程组，可得到河段内部断面的水力要素，然后利用微段方程，即可求出全部内部计算断面的未知数[8]。

3.2.2 三级解法

三级解法其思想是将问题归结于节点水位（或水位增量）的方程组，再求解节点间断面的水位、流量。此法相比于直接解法所需求解的代数方程组的阶数降得多，并且更加准确便捷[3]。

3.2.3 四级解法

四级解法是从三级解法的基础上提出来的。进一步从三级连接方程组中分离出外边界方程和汊点能量衔接方程，就可以得到以河网内部汊点水力要素为基本未知量的四级连接方程组[8]。四级解法所用机时要比三级解法直接消元所用的机时少，而且能够更有效的节省计算机存储量。

文献[11]对各种分级解法的推导和求解做了详细介绍。

3.3 矩阵标识法

矩阵标识法是在三级分解法的基础上，根据节点水位方程系数矩阵的高稀疏性，对矩阵非零元素进行标识[9]。按照代码指示，将非零元素用一维数组存储，排除零元素，求解时只对非零元素运算。该方法避免了零元素的处理，并以一维数组存储系数矩阵，提高了检索效率，整体上使方程组求解的效率大为提高[10]。但该方法未阐明系数矩阵与河网拓扑结构的关系，矩阵标识与求解之间具有强耦合关系，与面向对象程序设计提倡对象之间的低耦合性相左，增加了面向对象编程的难度，也降低了程序的灵活性和可维护性，限制了方法的应用和推广。

3.4 汊点分组解法

汊点分组解法的特点是能根据实际需要，将河网中的汊点分片分组编码后进行计算，对汊点方程组的系数矩阵进行压缩，使得压缩后的矩阵与分组后每组中的汊点数的阶数相同[12]。将河网汊点分组编码后进行计算，使得计算的工作量大幅度减少，节约了内存，提高了工作效率。

实际求解时，识别各河段与汊点之间的关系形成汊点方程组是比较困难的，如果将汊点分组，将会使得问题的复杂性进一步增加。另外汊点分组解法的递推计算相当复杂，程序编制计算难度大。

侯玉为解决上述问题提出了汊点分组新解法，其基本思想是利用矩阵的分块计算技术将一般分级解法形成的原汊点水位关系应用于汊点分组，从而使递推过程得到简化，这种解法具有较好的通用性[13]。

3.5 非线性方法

徐小明将树状河网的松弛迭代法应用到环状河网，将任意复杂的河网视为一系列的单一河道，而每一单一河道所形成的线性方程组系数都是五对角矩阵[14]。由于松弛迭代法是一条一条河道进行求解，所以可不对河道汇流节点进行编码、河道断面也不必全局编码，而且河道数目可以灵活增减，矩阵带宽减少从而提高计算精度。采用 Newton-Raphson方法直接求解非线性代数方程组，一般情况下收敛速度快，并且自动校正，也就是说前面迭代产生的误差并不会一步一步传递下去。这种方法的缺点是：对初始值的要求非常严格，只有迭代初值选取合适的时候，才能得到满足一定精度要求的解。

3.6 牛顿迭代解法

追赶法是经常用来求解差分格式的方法，在河网计算中，追赶法在很多情况下不通用。牛顿迭代解法在河网计算应用方面相比于追赶法有其独到的优势，并且具有一定的通用性[15]。河道断面的编码可以任意，使得处理一些较复杂的自然情况变得方便，另外这种方法的计算速度比较快，较好的满足了实践的要求。

3.7 汊点水位预测修正法

利用汊点水位预测修正法处理汊点处的回流效应，无需建立和求解整体分支河道方程组，则不需要求解大型稀疏矩阵所对应的代数方程组，因此节省内存空间；每个分支河道都能独立地进行计算，使得河道数目可以灵活增减；河道及计算断面编号简单方便，不需要进行节点优化编码；此法还适用于环状和树状河网并且对流动方向没有要求[16]。

文献[17]给出了汊点水位预测修正法（又称双松弛迭代法）求解河网水流的具体步骤。

上述这些求解方法在缓流状态下一般应用效果较好，但是当河段中出现急流或激波现象时，往往无法准确模拟[18]。后来又有学者提出，采用具有良好激波捕捉能力的 Godunov格式建立新的一维河网水动力数学模型。

4 结语

无论是哪一种数值解法求解偏微分方程，最终原问题都会被归结为线性方程组的求解。而且求解的精确度受到线性方程组系数矩阵特性的直接影响。河网非恒定流计算是非常复杂的，特别是考虑到实际应用的情况时，数值求解计算方法会变得复杂很多，仍然有许多问题需要学者们进一步研究，比如在建立汊点能量衔接方程时考虑水流运动及水环境变化规律。

[1] 卢士强,徐祖信.平原河网水动力模型及求解方法探讨[J].水资源保护,2003,(3)：5-9.

[2] 焦润红.河口围垦工程与一二维衔接水沙数学模型的研究[D].天津：天津大学建筑工程院,2005.

[3] 闫秀平,姚慧敏.一维河网非恒定流数值计算研究及其应用[J].河北水利,2014,(4)：33.

[4] 郭新蕾.河网的一维水动力及水质分析研究[D].武汉：武汉大学环境工程,2005.

[5] 顾元掞,王尚毅,郭传镇.具有岔道支流的明渠不恒定计算[J].天津大学学报,1995,(1)：54-64.

[6] 李岳生.网河不恒定流隐式方程组系数矩阵解法[J].中山大学(自然科学版),1977,(3)：27-37.

[7] 杨世孝,肖子良.河网不恒定流隐式方程组的稀疏矩阵解法[J].中山大学学报(自然科学学报),1994,(1)：61-68.

[8] 于丽丽.天津市北系河网洪水资源化蓄滞洪区蓄水研究[D].天津：天津大学建筑工程学院,2005.

[9] 李光枳,王船海.大型河网水流模拟的矩阵标识法[J].河海大学学报,1995,23(1)：36-43.

[10] 钱真,贾卫红,李世阳.河网水流模拟的矩阵标识法研究[J].人民长江,2014,45(14)：85-88.

[11] 白玉川,万春艳,黄本胜,等.河网非恒定流数值模拟的研究进展[J].水利学报,2000,(12)：43-47.

[12] 李义天.河网非恒定流隐式方程组的汊点分组解法[J].水利学报,1997,(3)：49-57.

[13] 侯玉,卓建明,郑国权.河网非恒定流汊点分组解法[J].水科学进展,1999,10(1)：48-52.

[14] 徐小明,何建京,汪徳,等.求解大型河网非恒定流的非线性方法[J].水动力学研究与进展,2001,16(1)：18-24.

[15] 张大伟,董增川,李少华.河网非恒定流计算的牛顿迭代解法[J].西北水利发电,2004,20(3)：31-33.

[16] 陈永灿,王智勇,朱德军,等.复杂河网水动力数值模型[J].水力发电学报,2011,22(2)：203-207.

[17] 姜伟,吉庆丰,宋振华,等.南方河网区引排水过程数值模拟研究[J].灌溉排水学报,2013,32(6)：91-95.

[18] 张大伟,权锦,马建明.应用 Godunov格式模拟复杂河网明渠水流运动[J].应用基础与工程科学学报,2015,23(6)：1088-1096.