Pontryagin最大值原理在一类最优控制问题中的应用

朱珊珊，罗 棋

（吉林师范大学 数学学院，吉林 长春 130000）

1 问题的提出

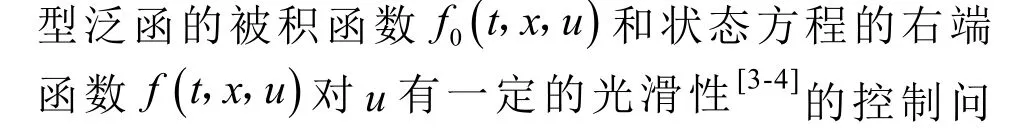
具体问题如下，一位5岁孩子的母亲，打算拿出积蓄的一部分10万元存入银行，年利率为10%，计算在孩子适婚年龄 25岁时取出这笔钱，并且要留下1万元用作一家人旅游的事宜。根据这位母亲的需要，每年至少支出0.5万元至多支出1.5万元作为孩子的日常开销。则 20年里从银行取出的总金额

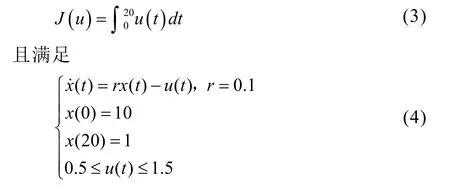
其中 x(t)表示第 t年存入银行的总钱数，u(t)第 t年支取的钱数。

该笔资金的最优管理问题即为使 20年后从银行取出的金额 J(u)最大，第 t年应支取多少u(t)。也就是寻求u( t)∈Ω，使得系统(3)-(4)成立，并使J(u)取最大值。本文先给出解决此类问题的一般方法。

考虑初始时刻和终止时刻已定，初端给定，终端自由的最优控制问题。

控制系统为(p)(1)目标泛函为混合型性能指标(2)。

2 问题的求解

为解决最优控制问题(1)-(2)，给出如下假设、定义和引理。

假设如下条件成立： f（ x， u）， Φ （x）是自变量的连续函数，

存在且连续。

f（ x， u）关于x满足Lipschitz条件，即当U1⊂U为有界集时，存在一个常数a＞0，使得对任意的 u∈U1，只要x1， x2∈Rn，都有

112

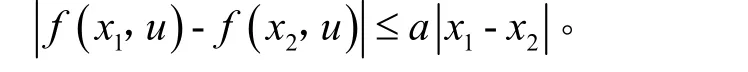
Ω中的函数u为分段连续函数，只有第一类间断点。

本文研究以混合型性能指标泛函为目标函数的控制问题，针对问题(1)-(2)给出如下引理。

引理 ［4］设 Φ （x）和f（ x， u）关于x具有连续的一阶偏导数，如果 u*（t）∈Ω和t1是使性能指标

为哈密顿函数。由此最优控制问题(1)及(2)得以解决。

3 应用举例

利用最大值原理求解上文中提出的个人理财问题。

哈密顿函数为

根据庞特里亚金最大值原理，u*( t)应使哈密顿函数达到最大值，因此

即最优管理策略为：在6年以前每年取0.5万元，6年以后每年取1.5万元，共取出24万元。

[1] 老大中.变分法基础[M].北京：国防工业出版社,2004：40-120.

[2] 钱伟长.变分法及有限元(上册)[M].北京：科学出版社,1980：110-137.

[3] 东北师范大学数学系,数学分析(下册)[M].北京：高等教育出版社,2010.6：324-328.

[4] 吕显瑞,黄庆道,最优控制理论基础[M].北京：高等教育出版社,2008：8-55.