Diophantine方程 x2 - 18 y2=1与 y2 - 2n z2= 16的公解

钱立凯

（曲靖师范学院 教师教育学院，云南 曲靖 655011）

方程

是一类重要的 Diophantine方程，其公解问题一直受到数论研究者的关注。

关于m=1，n=1时，方程组(1)的解的情况，目前结论还比较少[1-5]。m=1，n=4时，方程组(1)的解已有结果[6-12]；m=1，n=16时方程组(1)成为：

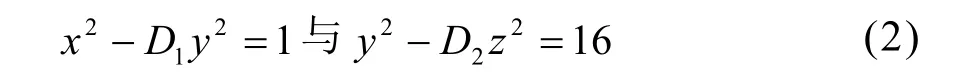
的解的情况，目前无相关结果。本文主要讨论

时方程组(2)的解的情况，即方程组

解的情况。

1 关键性引理

引理1[13]设p是一奇素数，则丢番图方程

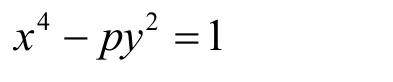
的正整数解只有

引理2设( xn, yn)，n∈Z为Pell方程

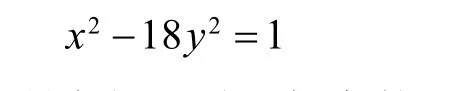
的所有解，则对任意的xn，yn具有如下性质：xn为平方数当且仅当n=0。

证明设( xn, yn)(n∈Z)是 Pell方程

的整数解。若 xn= a2，代入方程

可得

又由引理1知，方程

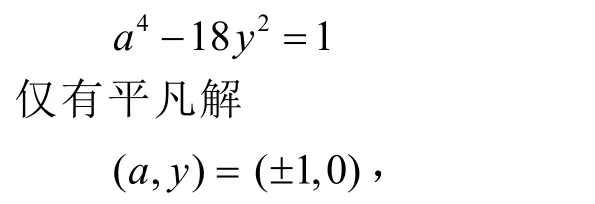
此时 xn=1，从而n=0；反之显然。

2 定理及证明

定理若n ∈ Z+，则Diophantine方程

情形1n为偶数

设n=2k，k ∈ Z+，则由方程(5)可得

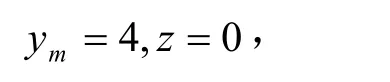
由此可得，当n为偶数时，方程组(3)只有公解

两两互素。由引理2知，xk-1为平方数仅当k=1，故k≠1时，xk-1不为平方数。又由(II)知，

不为平方数的2倍，所以此时(8)式无整数解，则方程组(3)无公解。

两两互素。

由引理 2知，xk为平方数当且仅当k=0，故k≠0时，xk不为平方数。又由(II)知，

不为平方数的2倍，此时(8)式无整数解，则方程组(3)无公解。

因为n为奇数，故(12)式左边为平方数的 2倍，(12)式右边为平方数的奇数倍，显然矛盾，故(6)式不成立，此时方程组(3)无公解。

综上所述，定理得证。

[1] Ljunggren W. Litt om Simultane Pellske Ligninger[J].Norsk Mat Tidsskr, 1941, 23： 132-138.

[2] Pan Jiayu, Zhang Yuping, Zou Rong.The Pell Equations x2-ay2=1and y2-Dz2=1[J].Chinese Quarterly Journal of Mathematics, 1999, 14(1)： 73-77.

[3] 乐茂华.关于联立 Pell方程方程组 x2-4D1y2=1和 y2-D2z2=1[J].佛山科学技术学院学报(自然科学版),2004,22(2)：1-3,9.

[4] 赵建红.关于Diophantine方程x2-8y2=1与y2-2nz2=1的公解[J].唐山师范学院学报,2016,38(5)：10-12.

[5] 普粉丽,万飞.Pell方程x2-15y2=1与y2-Dz2=1的公解[J].唐山师范学院学报,2017,39(2)：1-4.

[6] 胡永忠,韩清.也谈不定方程组x2-2y2=1与y2-Dz2=4[J].华中师范大学学报(自然科学版),2002,36(1)：17-19.

[7] 管训贵.关于Pell方程x2-2y2=1与y2-Dz2=4的公解[J].华中师范大学学报(自然科学版),2012,46(3)：267-269,278.

[8] 贺腊荣,张淑静,袁进.关于不定方程组 x2-6y2=1, y2-Dz2=4[J].云南民族大学学报(自然科学版),2012,21(1)：57-58.

[9] 杜先存,管训贵,杨慧章.关于不定方程组 x2-6y2=1与y2-Dz2=4的公解[J].华中师范大学学报(自然科学版),2014,48(3)：5-8.

[10] 杜先存,李玉龙.关于Pell方程x2-6y2=1与y2-Dz2=4的公解[J].安徽大学学报(自然科学版),2015,39(6)：19-22.

[11] 过静,杜先存.关于不定方程x2-12y2=1与y2-Dz2=4的解[J].数学的实践与认识,2015,45(9)：289-293.

[12] 过静,杜先存.关于 Pell方程x2-30y2=1与y2-Dz2=4的公解[J].数学的实践与认识,2015,45(1)：309-314.

[13] 柯召,孙琦.谈谈不定方程[M].哈尔滨：哈尔滨工业大学出版社,2011：64.