坦克行进间炮耳轴倾斜角预测模型研究*

宋泉良，卢志刚，王 维，王虎跃，胡冠华

（北方自动控制技术研究所，太原 030006）

0 引言

坦克在高低方向上进行瞄准时，火炮要绕炮耳轴在俯仰方向上作运动。当系统处于理想状态下时，火炮在与其垂直的同一个平面内运动，但当坦克在高速机动条件下行驶时，由于路面颠簸等原因，炮耳轴会发生倾斜，使射角减小并使得弹着点偏向倾斜一方，造成方向上和距离上的偏差，且倾斜角越大，偏差角亦越大［1］。目前的坦克火控系统对由炮耳轴倾斜引起的射击误差采取下述方法进行修正：火控计算机在进行解算时，首先，采集炮耳轴倾斜传感器输出的瞬时值（耳轴倾斜角）；然后利用文献［2-3］中的偏差角公式得到由炮耳轴倾斜引起的射击误差；最后根据该射击误差确定相应的修正量。现行方法仅考虑了炮耳轴在火控解算时的瞬时倾斜角，却忽略了下述情况：火控解算时，设炮耳轴倾斜角为α，但在火控解算至弹丸出膛的射击延时过程中，炮耳轴处于摆动状态，弹丸出炮口时刻的炮耳轴倾斜角很有可能偏离α，这将会导致火炮指向与规定的射击位置之间存在误差，影响坦克的射击精度。因此，对炮耳轴倾斜角进行预测便成了坦克火控领域的研究重点。

灰色理论具有计算简单、适用于小样本数据预测的特点，能够较好地满足火控系统的实时性需求。GM（1，1）模型是灰色理论中最具代表性的模型。为了提高其预测精度，许多学者从多方面对模型进行了改进。在原始序列的单调性处理方面，文献［4］通过加速平移变换，文献［5］通过加速指数变换，使变换后的数据具有单调性。在背景值改进方面，文献［6］利用数值积分和插值构造背景值，文献［7-11］利用GM（1，1）模型的时间响应函数直接构造背景值，文献［12］通过Simpson公式构造背景值。为了准确预测具有振荡性特点的炮耳轴倾斜角数据，本文提出了一种改进的灰色模型。首先，综合y=arccosx和y=cosx的函数特点进行数据变换，得到正数单调序列；然后，重构了模型背景值，并分析了重构背景值中的参数与模型参数的关系；最后，构建了新的灰色微分方程。经过在具体实例中的应用，结果表明改进模型对炮耳轴倾斜角的预测具有较高精度。

1 数据变换及检验

GM（1，1）模型适用于对正数单调序列的预测，但利用倾斜传感器得到的炮耳轴倾斜角数据呈现振荡性，因此，需要对原始序列进行数据变换。本文在基于短暂射击延时过程中炮耳轴倾斜角变化平稳的假定下，利用y=arccosx的非负性和y=cosx的周期性对初始序列进行正数化和单调性处理。

1.1 数据变换

由于y=arccosx的值域为［-1，1］，所以，先对原始序列进行数值压缩处理，得到，其中：

设经单调性处理后得到的正数递增序列为，处理步骤如下：

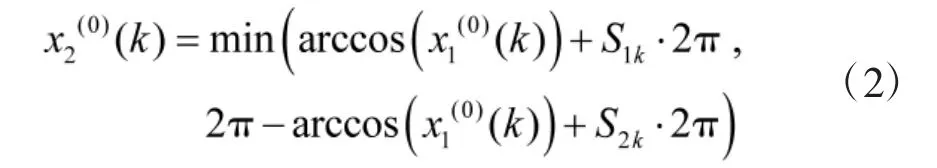
1）当时，，当时，；

2）当时（k=2，3，…，n）：

其中，S1k为使前者取值大于的最小整数值，S2k为使后者取值大于的最小整数值。

当时（k=2，3，…，n）：

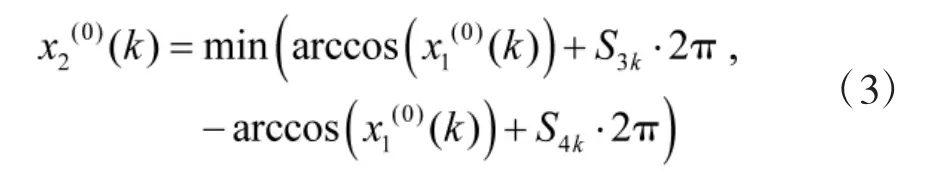
其中，S3k、S4k的作用同 S1k、S2k。

1.2 数据检验

经数据变换后的序列还需要通过光滑度检验，才能够通过灰色模型取得较好的预测效果。

定义1.1设序列，则称ρ（k）为序列X的光滑比，其中［13］。

定义1.2若序列满足：ρ（k）递减且当 k＞3 时，其中 ε＜0.5，则称序列X具有准光滑性［13］。

2 改进灰色模型

定义2.1设为原始数据序列，为的一次累加生成序列，为背景值序列，其中，［13］。则称 GM（1，1）的灰色微分方程为：

称GM（1，1）的白化微分方程为：

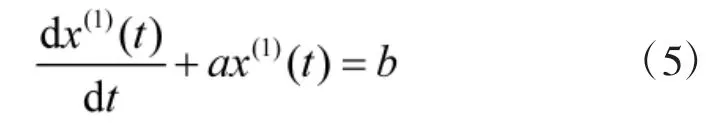
a称为模型的发展系数，它的大小及符号反映了的发展趋势，b称为模型的协调系数，它反映了数据间的变化关系。参数列与由最小二乘法求解，，其中：

利用求得的参数，解白化微分方程可得模型的时间响应函数。

2.1 背景值构造及其参数的表达

对式（5）两边在区间［k-1，k］上同时积分可得：

将上式与式（4）对比可得

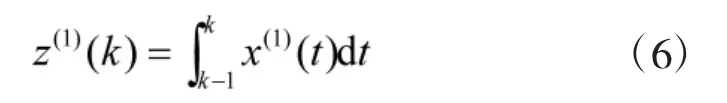
通过式（6）与式（4）可以看出，式（4）构造的背景值是梯形的面积，但实际背景值则是由式（6）所表示的曲线在区间［k-1，k］上与坐标轴 t所围成的曲边梯形面积，两者之差即为传统GM（1，1）模型背景值构造形式的误差。

传统GM（1，1）模型中背景值的构造方法属于平滑生成，当数据序列增长较快时，会存在较大的滞后误差。本文背景值的构造参照文献［14］中的方法：将区间［k-1，k］等间隔分为n份，通过这些小区间的矩形面积叠加来拟合真实面积，背景值公式为：

n的取值直接影响背景值的大小，进而影响模型的预测精度。易知，当n取值较小时，拟合面积小于真实面积；当n取值较大时，拟合面积大于真实面积。所以，在n由小到大的过程中，必然存在使得拟合面积等于真实面积的n值。

在现有的研究中，对n值的选取主要有两种方法：经验公式法和试探法。前者虽使计算简化，但所得模型精度较差；后者所得模型的预测精度较前者有所提高，但计算用时较长。本文在基于无偏性的准则下，研究了n与模型参数之间的关系，提出了n值的直接表达式。

由式（6）和灰色微分方程的通解可得到具有无偏性的背景值：

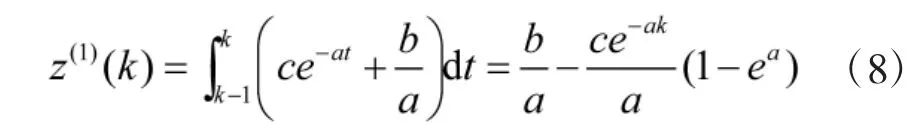
由式（7）和式（8）可得：

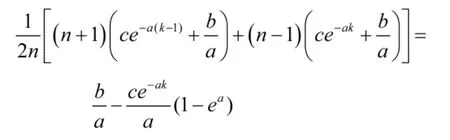
解得：

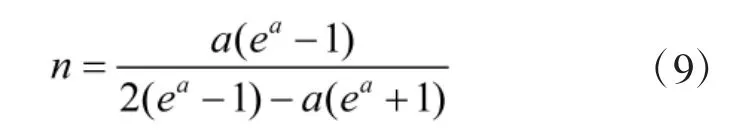
2.2 改进灰色微分方程及预测公式求解

将式（7）和式（9）代入式（4）可得优化的灰色微分方程：

其中：

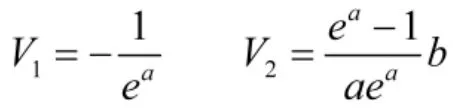
令

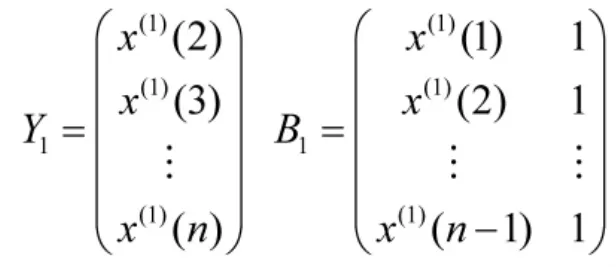
参数由最小二乘法求得：Q1=（B1TB1-1）B1TY1，进而可得到参数列Q：

将 a，b 代入式（5），且令可得的预测公式：

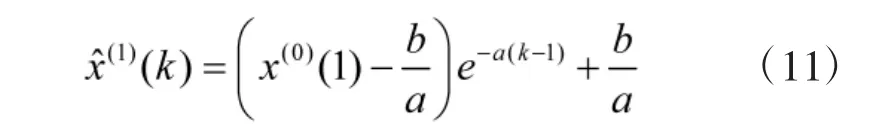
还原数据得：

2.3 改进灰色模型的建模步骤

具体建模步骤为：

Step1：将原始序列分别进行数值压缩处理、正数化和单调性处理，得到正数递增序列；

Step2：对序列进行光滑性检验，若满足准光滑性，则通过一次累加生成得到序列；

Step3：重构背景值，并得到背景值中参数的表达式；

Step4：结合Step3构建新的灰色微分方程，并进行模型参数的求解，得到的预测公式；

Step5：对上一步结果进行数据还原，得到的预测公式。

3 实例分析

为了验证改进的灰色模型能够准确预测炮耳轴倾斜角的变化，下面将已经处理的某型坦克行进间炮耳轴倾斜角的仿真数据作为数据源，数据见表1。本文将采用动态预测处理方法，即先以前6个数据作为原始序列来预测第7个数据，然后再以第2个至第7个数据作为原始序列来预测第8个数据，以此类推。

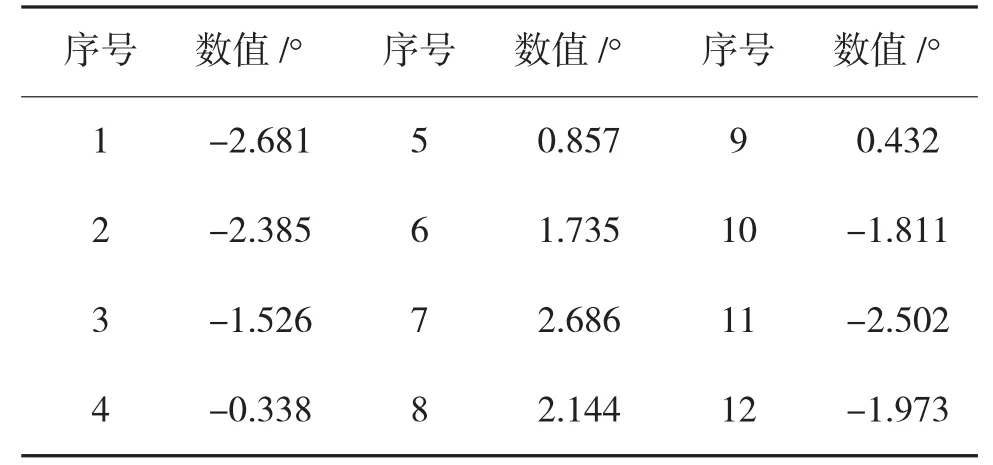
表1 炮耳轴倾斜角数据

以第一次预测为例：

原始序列为：

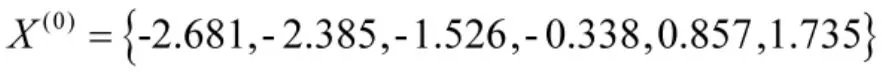
1）经数据预处理后，可得正数递增序列：

2）经检验，具有准光滑性，故对其进行一次累加生成得到。代入式（10），通过最小二乘法求得参数列Q1，利用两个参数列的转换关系可得到参数列Q。

4）将参数列Q中的a、b值代入式（12），可得前6个数据的拟合值和第7个数据的预测值：

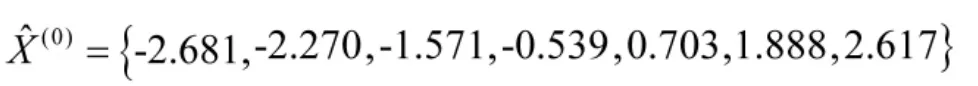
3）将

重复以上步骤，可继续得到第8个至12个数据的预测值，即得到完整的（0），见表 2。

表2 改进模型的拟合及预测结果

为了验证改进模型具有较好的预测精度，对以下3个模型的预测结果进行比较：将传统GM（1，1）模型作为模型1，将本文中的数据变换方法与试探法求取n值相结合的预测模型作为模型2，改进模型作为模型3。对比结果见表3及表4、图1所示。

由表3可得，传统模型不适用于对振荡序列进行预测，而经过数据变换后的改进模型对振荡序列具有较好的预测效果。由图1和表4可得，模型3的预测结果较模型2具有较小的误差，并且模型3预测结果的平均相对误差为3.53%，模型2则为4.42%，以上表明本文中对于背景值参数n求取方法优于试探法。因此，改进模型有助于对炮耳轴倾斜角的预测。

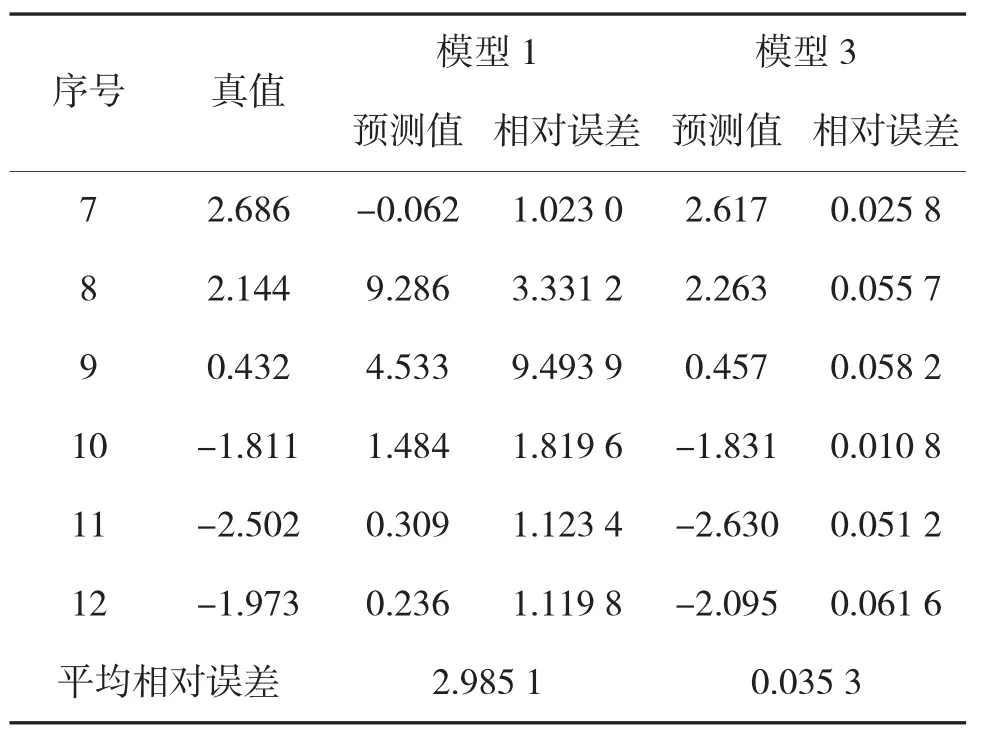
表3 模型1、模型3的预测结果

表4 模型2、模型3的预测结果

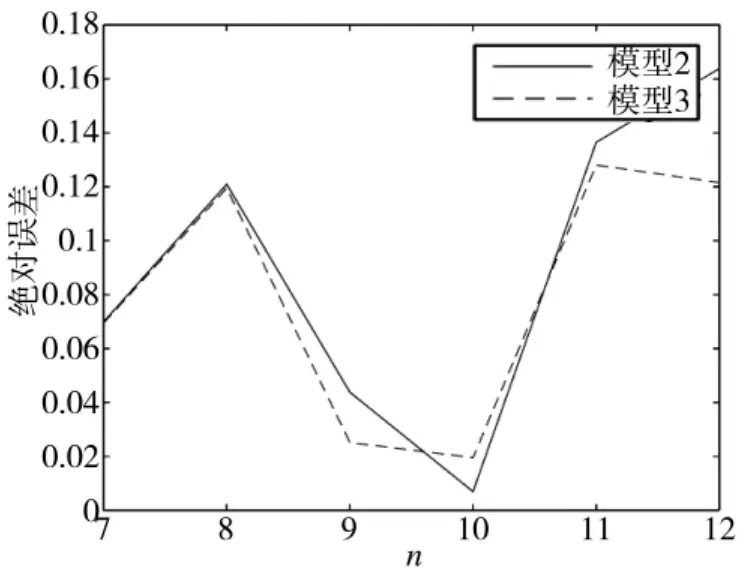
图1 模型2、模型3预测结果的绝对误差曲线

4 结论

坦克在高速通过颠簸路面时，火炮耳轴倾斜角数据呈现振荡性。因此，传统GM（1，1）模型不能直接用于炮耳轴倾斜角的预测。本文通过数据变换、对重构背景值中参数的求取方法和灰色微分方程进行改进，提出了一种能够准确预测炮耳轴倾斜角变化的改进灰色模型。通过具体应用，改进的灰色模型具有较高的预测精度，其预测结果的平均相对误差为3.53%，为通过智能射击门控制解决坦克火控系统的射击延时误差奠定了基础。

［1］霍李，王媛，刘景江.炮身俯仰过程中的类摇摆现象分析［J］.火力与指挥控制，2016，41（3）：158-160.

［2］杨凤岗.用象限仪标定炮耳轴倾斜传感器的误差分析［J］.火力与指挥控制，2008，（33）4：124-127.

［3］曹宁，王晓锋，徐亚栋.车载炮操瞄精度分析与检验［J］.火力与指挥控制，2012，37（11）：147-148.

［4］钱吴永.数据变换技术与 GM（1，1）模型研究［D］.南京：南京航空航天大学，2008.

［5］崔立志.灰色预测技术及其应用研究［D］.南京：南京航空航天大学，2010.

［6］李俊峰，戴文战.基于插值和Newton-Cores公式的GM（1，1）模型的背景值构造新方法与应用［J］.系统工程理论与实践，2004，12（10）：124-125.

［7］罗党，刘思峰，党耀国.灰色模型 GM（1，1）优化［J］.中国工程科学，2003，5（8）：50-53.

［8］ ZHOU P，WEI Y.The optimization of background value in grey model GM（1，1）［J］.Journal of Grey System（TW），2006（2）：133-136.

［9］杨知.GM（1，1）模型的优化及其应用研究［D］.南京：南京航空航天大学，2008.

［10］WANG Z X，DANG Y G，LIU S F.Optimization of background value in GM（1，1）model［J］.Systems Engineering——Theory&Practice，2008，28（2）：61-67.

［11］李星毅，李奎，施化吉，等.背景值优化的 GM（1，1）预测模型及应用 ［J］. 电子科技大学学报，2011，40（6）：911-914.

［12］YANG J X，ZHANG Y.Micro-mechanical gyro drift modeling based on GM （1，1）of reconstruction of background［C］//Proceedings of the 2009 IEEE International Conference on Grey Systems and Intelligent Services，2009：7-12.

［13］刘思峰，杨英杰，吴利丰.灰色系统理论及其应用［M］.北京：科学出版社，2014.

［14］谭冠军.GM（1，1）模型的背景值构造方法和应用［J］.系统工程理论与实践，2000，28（4）：98-103.