基于CATIA的克林贝格C50铣齿机切齿加工仿真应用

肖将,秦厚明,王传法,麻俊方

(1.中国重汽集团技术发展中心，山东济南 250001；2.中国重汽集团济南桥箱有限公司，山东济南 250001)

0 引言

螺旋锥齿轮是重型汽车车桥的重要零部件，其齿制可分为格里森制、奥利康制、克林贝格制3种，长期以来行业内主要采用格里森制。近年来，随着切削技术的进步以及干切技术的应用，奥利康制连续切削生产方式的优点得到体现，获得了更多的生产应用。目前，国内主要车桥生产企业已经大量引进了加工奥利康制齿轮的全数控机床。

文中的研究对象是克林贝格C50铣齿机的切齿加工仿真。C系列机床是克林贝格和奥利康公司合并后推出的产品，是国内最新式的摆线齿数控加工机床。文中的研究目的是通过分析该设备的加工原理，进行切齿加工仿真，建立被加工齿轮的齿面模型，为工厂的生产准备以及进一步的齿轮强度、动态性能等分析提供依据。

摆线齿准双曲面齿轮引入市场前后，这项技术的理论研究也得到了相应的发展。在准双曲面齿轮的加工仿真方面，主要有两种解决方法：(1)采用数学方法，根据曲面啮合原理建立齿面方程。例如聂少武介绍了刀倾全展成法加工、采用产形轮理论建立数学模型的方法[1]。(2)采用三维建模软件进行模拟加工。文中采用的是这种方法。具体仿真方法可根据不同铣齿机的加工原理、是否采用刀倾、加工方法为成形法还是展成法、不同仿真软件的选择(VERICUT、UG、CATIA、Pro/E等)、产形轮的类型及建模方法等而有所不同。例如汪中厚[2]介绍了基于CATIA环境的弧齿锥齿轮加工仿真方法。

1 C50铣齿机加工原理及机床坐标系建立

克林贝格C50铣齿机为立式加工机床，采用六轴数控，包括A、B、C、X、Y、Z6个联动坐标，X为刀盘轴线的垂直运动，Y为刀盘轴线的水平运动，Z为工件轴线的直线运动，A为刀盘主轴的回转，B为工件绕自身轴线的转动，C为工件主轴的转动。与机械式铣齿机相比，取消了摇台、偏心机构、刀倾机构等，使结构大为简化,如图1所示。齿轮设计及机床调整算法由KIMOS软件实现，切齿工具采用SPIRON系列刀盘。加工方式采用刀倾半展成法，即大轮采用仿形法、小轮采用有刀倾的展成法加工。与摇台式机床不同，C系列机床的刀倾以及展成过程要通过数控的多坐标联动来实现。

C50机床系统将六轴坐标转化为类似摇台式机床的通用定位参数，并显示在人机交互界面上,如刀转角、刀倾角、摇台角、刀位、床位等,因此仍需按照类似摇台式机床的方式建立切齿加工坐标系。

虚拟的摇台坐标系SM和工件坐标系S1的相对位置如图2 所示。其中l为机床中心到交叉点距离,aη为机床偏置,aγ为机床根锥角,aχ为床位。

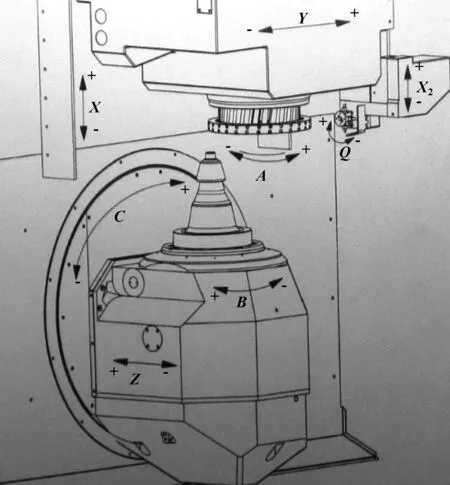
图1 C50机床各自由度示意图

图2 工件坐标系与摇台坐标系的相对位置

摇台坐标系SC1、刀倾坐标系Sd和刀转坐标系Sb的相对位置如图3所示,其中σ为刀转角，αm为摇台角。

图3 摇台坐标系SC1、刀倾坐标系Sd和刀转坐标系Sb

刀盘坐标系Sf与刀倾坐标系Sd的关系如图4所示,其中τ为刀倾角。

图4 刀盘坐标系与刀倾坐标系

刀盘坐标系Sf与摇台坐标系SM的关系如图5所示,其中M为切齿参考点，u为参考点沿刀刃方向的位移，θ为刀盘转角。

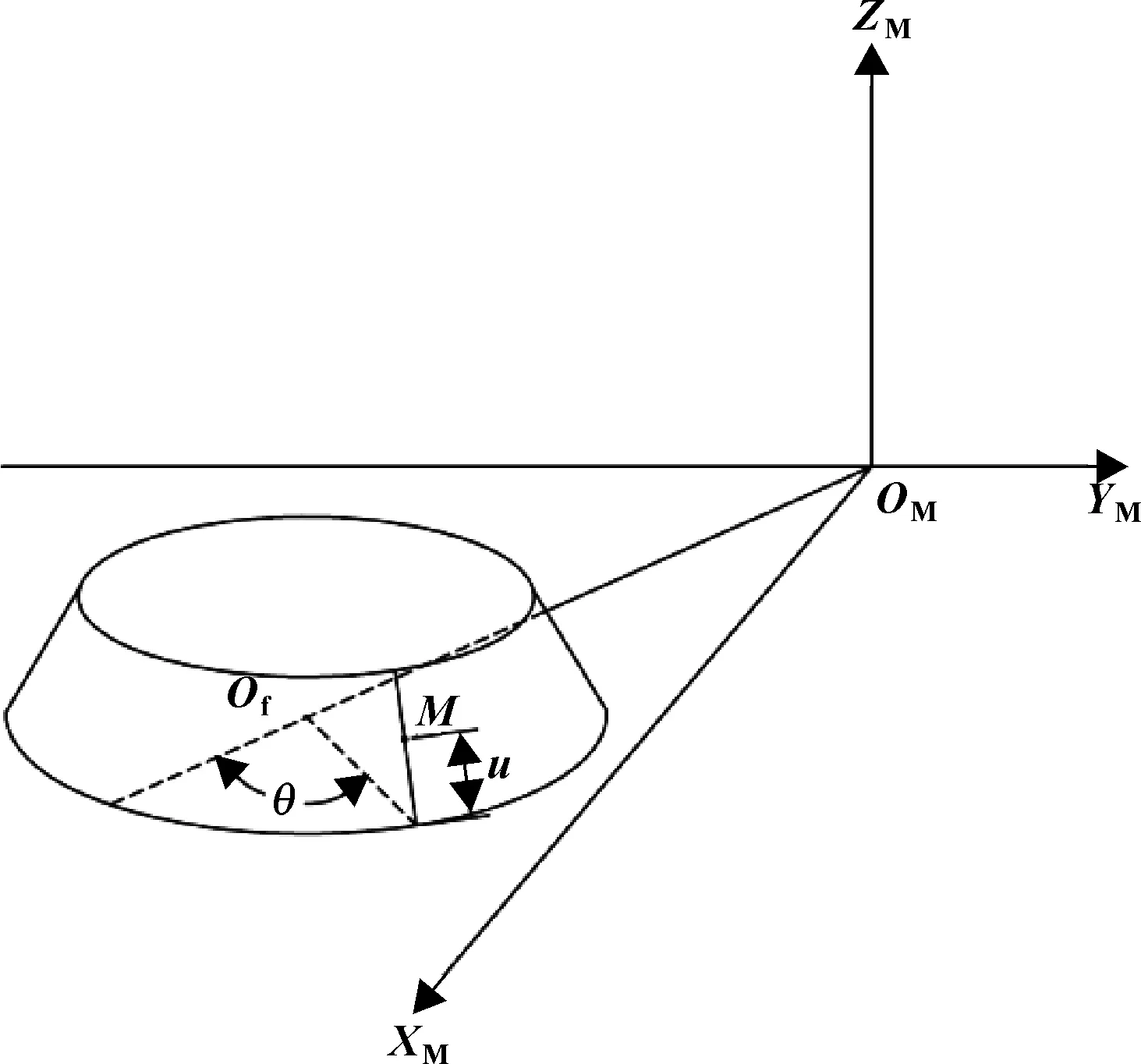
图5 刀盘坐标系与摇台坐标系

对于大齿轮刀盘的安装，可令刀倾角、刀转角等于0。

2 小齿轮的切齿加工仿真

2.1 展成法加工原理

克林贝格C50铣齿机采用展成法加工小齿轮，该过程分为两步：首先令摇台角恒定，切入到全齿深，然后开始展成过程。摇台角到达到程序设定值时展成过程结束。

在小齿轮展成阶段，存在刀盘、摇台、工件同时绕自身轴线的转动。机床数控系统通过配置上述3种运动的相对转速，模拟出产形轮的齿廓，并实现连续分齿，从而在工件上产生范成的齿面。与摇台式铣齿机不同，C50铣齿机模拟摇台的回转运动，是通过几个坐标轴联动来实现的。

刀盘和轮坯位置可根据机床安装参数如刀倾角、刀转角、摇台角、刀位、床位等进行定义，如图6所示。

图6 小齿轮加工刀盘和轮坯相对位置

2.2 加工仿真原理和产形轮建模

文中采用的小齿轮仿真方法不是直接模拟刀盘的运动，而是通过建立虚拟的产形轮模型，令产形轮与工件按固定速比运动，并通过布尔运算模拟切齿过程来实现的。

摆线齿准双曲面齿轮的产形轮建模可采用多种方法。邹旻等人[3]用矢量运算方法推导了平顶产形轮齿面方程，得到了齿面的数学模型。文中采用的产形轮形式为锥形顶面，并采用MATLAB软件编程来完成矢量运算。

在MATLAB环境中建立内外刀刃上任意点的轨迹方程，用曲面工具surfc命令形成曲面。程序流程如图7所示。

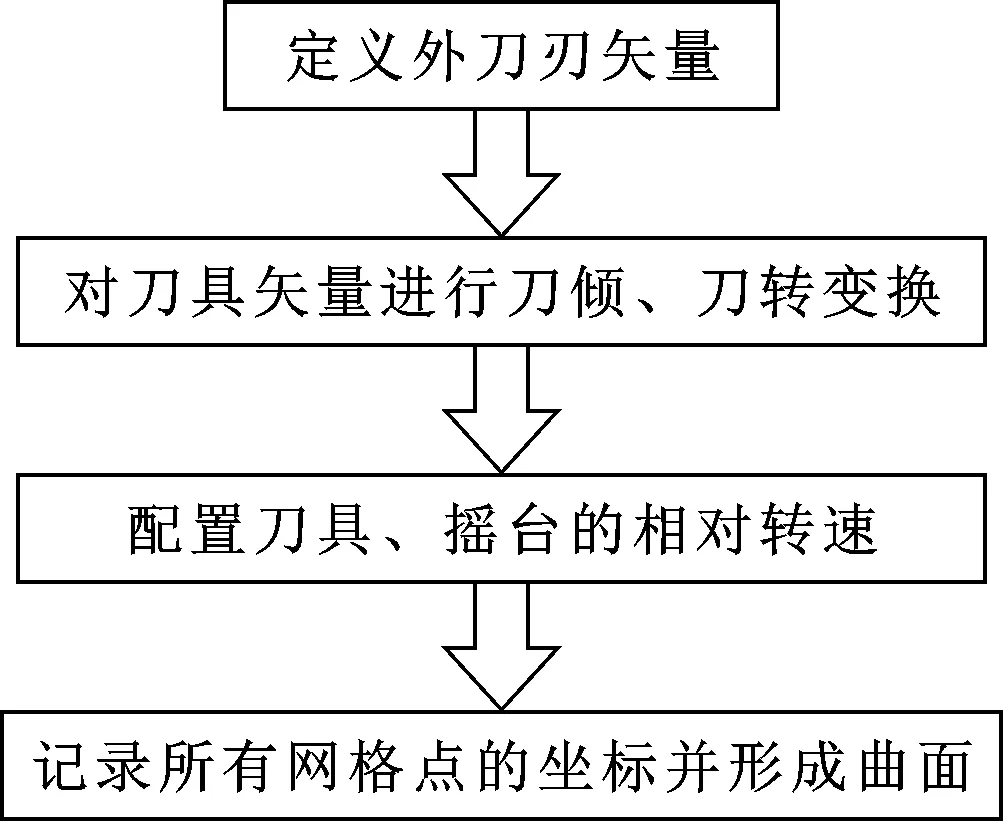
图7 程序流程

求解外刀形成的产形轮齿面时，程序内容如下：

fi=αm; //αm摇台角

Ex0=[aφ,0,0]; //aφ为径向刀位

Ex=R(k,fi,Ex0); //k为Z轴单位矢量

alpha=φv; //φv外刀条角度

r0=[ rw,0,0]; //rw 刀盘半径

F=[-sin(φv),0,-cos(φv)]; //φv为外刀条角度

u=linspace(0, TA,2); //TA为切入深度

theta=linspace(-theta0, theta0,30);

eta=σ; //σ为刀转角

ksai=τ; //τ为刀倾角

jq=R(k, σ,Ex/249);

kq=R(jq, τ,k);

ip0=ZP/Z0;

2017年广州日报应势而动，主动针对印务板块调结构、去产能，实施整合优化。在削减报纸印刷产能的同时，加大书刊印刷、商业印刷市场的拓展力度。未来的广州日报会坚持两手抓，全力拓展线上传播，同时坚守传统影响。“只要能触达用户，一切应用皆是媒体，信息传播载体间不是非此即彼的关系，用户对资讯的消费需求是多层次、多样化的，未来的传播会是全方位、多渠道到达的复合形态。”郭献军反复强调。

for i1=1:length(u)

for j1=1:length(theta)

rf=R(k, αm+α1,r0+u(1,i1)*F);

rp0=R(k, σ,rf);

rp1=R(k,(0+ip0)*theta(1,j1),rp0);

rp2=R(jq, τ,rp1);

rp3=Ex+rp2;

r=R(kk,1*theta(1,j1),rp3);

x(i1,j1)=r(1,1);

y(i1,j1)=r(1,2);

z(i1,j1)=r(1,3);

end

end

surfc(x,y,z);

上述程序中，R(a,b,c)为矢量旋转函数。表示矢量c以矢量a为轴线旋转角度b。涉及的其他参数可在C50铣齿机显示界面中查到。

同理可得到内刀形成的齿面方程。

基于上述内外刀形成齿面的数据，在三维建模软件中构建产形轮模型，如图8所示。

图8 产形轮齿形

假想产形轮与工件的安装位置如图9所示。

图9 产形轮和轮坯相对位置

2.3 在CATIA环境中完成加工仿真

齿轮加工是在齿坯上去除材料的过程，在CATIA中可以通过布尔运算来实现。刀刃啮合点在齿坯上的相对运动轨迹就是被加工齿面。

小齿轮仿真流程如图10所示。

图10 小齿轮仿真流程

主从动齿轮的三维仿真结果如图11所示。

图11 加工仿真完成的小轮齿形

3 大齿轮的切齿加工仿真

采用成形法原理构建加工仿真模型的步骤是：首先建立刀盘模型，按照机床调整参数放置刀盘和工件，采用布尔运算功能和宏命令实现循环切齿。加工时需保证齿轮、刀盘的转速比，从而实现加工过程的自动分齿。

3.1 建立刀盘模型

根据克林贝格的Spiron 系列刀盘的刀片组数、内外刀角和刀顶距等参数，建立刀盘的三维模型，如图12所示。刀盘包括17组刀齿，每转过一组刀齿时，被加工齿轮转过一个齿间。

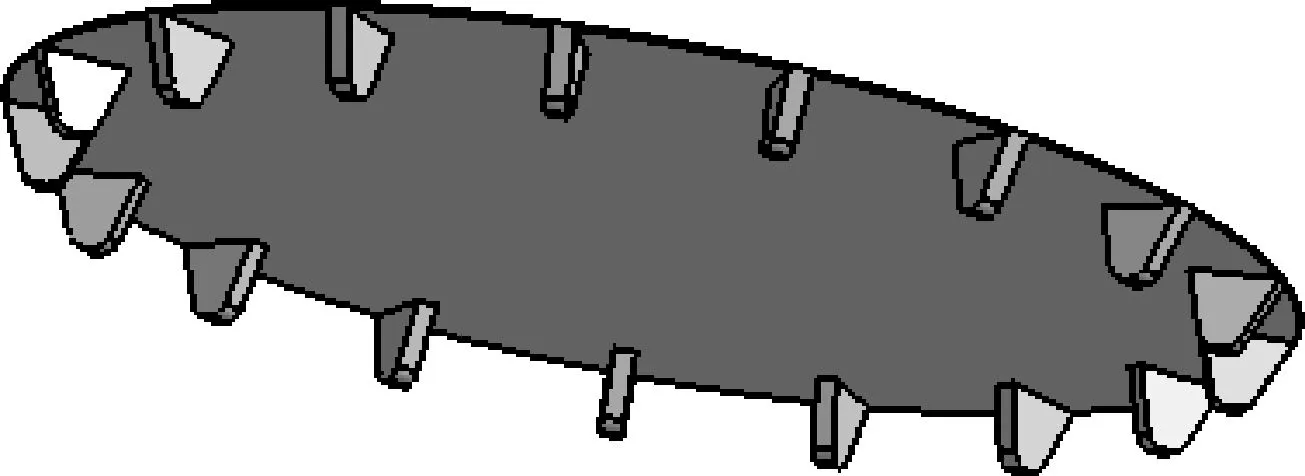
图12 刀具外形和安装参数图示

3.2 刀盘和大轮齿坯的安装位置

与小轮加工工艺相比，大齿轮刀盘无刀倾角、刀转角。根据摇台角αm可确定刀盘的安装位置。刀盘和工件相对位置如图13所示。

图13 从动齿轮加工刀盘和轮坯相对位置

3.3 大轮加工仿真流程

在CATIA环境中，大齿轮加工仿真流程如图14所示。

图14 大齿轮加工仿真流程

大齿轮的三维仿真结果如图15所示。

图15 加工仿真完成的从动齿轮齿形

4 应用实例

文中的算例是一对速比为37/11的主减速器齿轮副，机床加工调整参数如表1所示。

表1 C50铣齿机用摆线齿准双曲面齿轮的齿形和机床调整参数

零件实物如图16—图17所示。

图16 小齿轮齿形

图17 加工完成的从动齿轮齿形

5 结论

在CATIA环境中实现了刀倾半展成法加工摆线齿准双曲面齿轮的仿真过程。对比仿真模型和齿轮成品，可见齿形一致，从而证明了建模方法的可行性。该方法的特点是仿真过程直观，便于通过改变机床调整参数进行模拟试切，有利于提高设计和生产效率。仿真得到的三维模型可以作为进一步的齿轮精度、强度、动态性能分析的基础。

参考文献:

[1]聂少武,邓效忠,李天兴.奥利康准双曲面齿轮的理论齿面推导及仿真[J].机械传动,2009(2)：109-112．

NIE S W,DENG X Z,LI T X.Theoretical Tooth Surface Deduction and Simulation of Orion Hypoid Gear[J].Journal of Mechanical Transmission,2009(2):109-112．

[2]汪中厚．准双曲面齿轮动态性能仿真[M]． 北京:科学出版社，2006：150-162.

[3]邹旻,丁军．摆线齿锥齿轮的产成原理及其产形面方程[J]．机械传动， 2011(6):31-33．

ZOU M,DING J.The Principle of Epicycloidal Bevel Gears and Their Generating Gears[J].Journal of Mechanical Transmission,2011(6):31-33．